基于双PH曲线五轴线性刀具路径光顺轨迹生成及其参数同步方法

陶廷江, 韩 江, 姜 阳, 卢 磊, 黄晓勇, 夏 链

(1.合肥工业大学 机械工程学院,安徽 合肥 230009;2.安徽省智能数控技术及装备工程实验室,安徽 合肥 230009)

0 引 言

五轴数控机床由3个直线轴和2个旋转轴构成,具有刀具加工姿态灵活、加工效率高、加工质量好等优点,广泛应用于航空航天发动机叶轮叶片、汽车涡轮增压器叶轮、飞机结构件等复杂曲面类零件的加工[1-2]。目前五轴数控机床加工轨迹多由CAM软件生成线性加工路径组成,线性路径拐角处速度、加速度和加加速度不连续,导致机床在拐角处将运动速度降低至0,从而产生频繁加减速,导致加工效率和加工质量的下降。因此,研究五轴线性刀具路径光顺处理对提高五轴数控机床的加工效率和加工质量具有重要意义。目前国内外学者对线性刀具路径光顺研究主要分为两大类:

(1) 全局光顺。全局光顺是利用高阶参数曲线拟合刀位点,包含插值过渡[3-4]和近似逼近[5]等方法。全局光顺能确保整条路径的连续性,但难以严格约束样条路径与原小线段路径之间的误差,且全局光顺的计算量较大,限制了实时应用效果[6]。

(2) 局部光顺。局部光顺利用高阶连续曲线转接光顺原有线性轨迹的拐角,以避免拐角处切向不连续。局部拐角光顺方法可实现光顺误差可控且曲线几何参数实时计算,是一种广泛使用的线性路径光顺方法[7]。

下面主要对局部光顺进行国内外现状阐述。文献[8]利用双三次Bézier曲线在机床坐标系下对直线轴和旋转轴进行光顺处理,但需要通过雅克比矩阵将工件坐标系下的近似误差映射到机床坐标系下;文献[9]采用2条(Pythagorean-hodograph,PH)曲线分别对刀尖点和刀轴上一点进行光顺,但未考虑刀轴矢量数据的单位化;文献[10]利用双五次B样条曲线分别对工件坐标系下笛卡尔坐标系内刀尖点线性路径和单位球面上刀轴矢量线性路径进行光顺处理;文献[11]利用双三次NURBS曲线分别对刀尖点平移轨迹和刀轴方向轨迹进行拐角光顺,获得了满足预设近似误差约束和G2连续性的五轴光顺轨迹,但没有讨论刀轴矢量近似误差;文献[12]利用双七次B样条分别对工件坐标系下刀尖点线性路径和机床坐标系下刀轴方向线性路径进行光顺;文献[13]提出一种双B样条曲线对刀尖点和刀轴方向线性路径进行光顺,并通过外接转角光顺方式降低拐角处曲率;文献[14]使用双B样条曲线分别对工件坐标系下笛卡尔坐标系内刀尖点和单位球面内刀轴方向子轨迹进行光顺;文献[15]使用双七次PH曲线分别对工件坐标系下刀尖点和机床坐标系下刀轴方向线性路径进行光顺处理,并将残余直线段表示成样条曲线,获得了C3连续的五轴线性光顺轨迹;文献[16]创建了Airthoid曲线,并光顺了工件坐标系下刀尖点和机床坐标系下刀轴矢量线性路径,获得了光滑的五轴光顺轨迹;文献[17]提出了一种两步实时解耦的五轴刀轨局部光顺算法,并通过单位长度冲激响应滤波器获得各轴加速度连续的进给速度。

本文提出一种五轴线性刀具路径局部拐角光顺方法,生成G2连续的光顺轨迹并实现其参数同步。引入2条五次PH曲线在工件坐标系下分别对刀尖点子轨迹和刀轴矢量子轨迹进行光顺,且刀轴矢量近似误差可通过一种简单的解析方法进行控制。在采用线性同步(刀尖点曲线和刀轴矢量曲线使用同一参数)的情况下,对PH曲线的控制点进行调整,使刀轴矢量在转接曲线和原始轨迹的衔接点处一阶和二阶导数连续,避免刀轴矢量在衔接点处的运动突变。本文提出的光顺方法不涉及工件坐标系和机床坐标系之间的运动学变换,计算效率高,且刀尖点误差和刀轴矢量误差可直接控制,刀轴矢量变化连续,具有重要的工程实际意义。

1 五轴路径光顺

1.1 PH曲线拐角过度

PH曲线是一种特殊的多项式参数曲线,其参数与弧长之间有解析表达关系。这将简化参数与弧长之间映射的建立过程,有利于实现高精度高效率加工。下面首先介绍PH曲线的构造。

设平面中n次Bézier曲线Q(ξ)定义[7]如下:

(1)

其中:bi为Bézier曲线的控制点Bi的位置矢量，下文同;ξ为曲线参数,ξ∈[0,1]。当该Bézier曲线满足如下条件时,则称其为PH曲线，即

x′(ξ)=u2(ξ)-v2(ξ),

y′(ξ)=2u(ξ)v(ξ),

u(ξ)=u0(1-ξ)2+2u1(1-ξ)ξ+u2ξ2,

v(ξ)=v0(1-ξ)2+2v1(1-ξ)ξ+v2ξ2,

σ(ξ)=u2(ξ)+v2(ξ)

(2)

其中,σ(ξ)为弧长s关于参数ξ的变化率,即

(3)

PH曲线曲率的计算公式为：

(4)

就PH曲线而言,为得到拐角过渡曲线与原始直线段连接处G2连续性,最低阶次为5次[18]。设在局部平面直角坐标系OTN中,Q(ξ)=x(ξ)T+y(ξ)N,则5次PH曲线的控制点满足如下关系:

(5)

通过调整单位矢量T,使得T方向由B0指向B1,并调整控制点使得b1=b2,b3=b4,得到衔接点处曲率值κ(0)=κ(1)=0。此外,原始直线段曲率为0,由此可得过渡曲线和原始直线段曲率连续,即G2连续。

由(4)式、(5)式可得v0=v1=u1=0,PH曲线可简化为:

(6)

以直线L0V和VL1构成的拐角为例,阐述PH曲线光顺线性路径过程,如图1所示。其中：β为该拐角夹角；θ为该拐角外角；h、k为过渡长度且h=k。

由Bézier曲线的凸包性可知,PH曲线拐角最大误差在其中点处产生,表示为:

(7)

其中

μ=2(17+18cosθ);

λ=h-k+36k(1+cosθ);

1.2 刀尖点路径光顺

1.2.1 误差可控的转角过渡

假设在刀位点Pi-1、Pi、Pi+1构成的平面内,在拐角∠Pi-1PiPi+1处引入五次PH曲线,并使用上节所述方法确定PH曲线参数。

通过给定光顺误差ε计算相应过渡长度k,进而可计算误差可控的过渡PH曲线[7]。k的计算公式为：

(8)

其中,δ=1+cosθ。

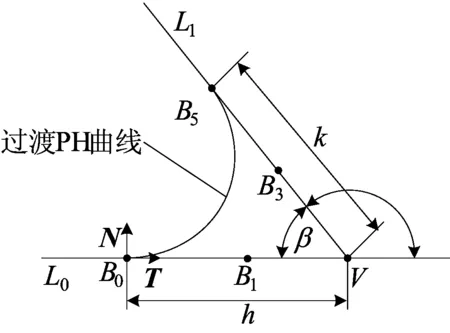
图1 PH曲线拐角光顺

1.2.2 过渡长度控制

仅由近似误差确定过渡长度时,在相邻拐角处可能会有光顺曲线重合,如图2所示。

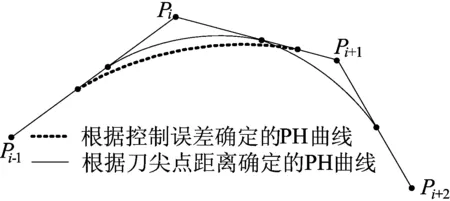
图2 过渡长度对PH曲线拟合的影响

因此需根据近似误差和原直线段长综合确定PH曲线的过渡长度,即设定相邻刀位点间过渡长度不超过原直线段长的1/2。总之,在轨迹中间,每2个相邻拐角间插入2段PH曲线,而轨迹两端相邻刀位点间只插入1段PH曲线,应区别对待。

考虑相邻刀位点距离的过渡长度l计算方法如下：

其中,h为仅考虑控制误差的过渡长度。

1.3 刀轴矢量路径光顺

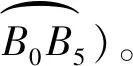
(9)

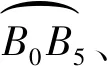
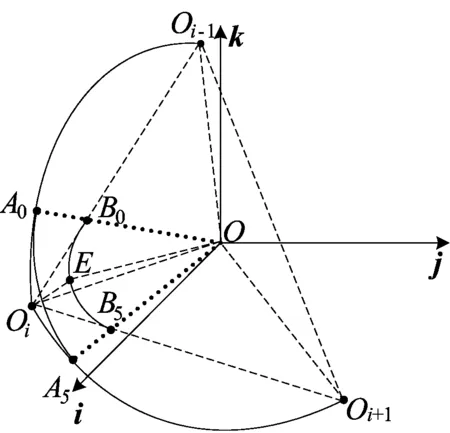
图3 刀轴矢量转接光顺

1.3.1 刀轴矢量近似误差控制

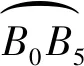
图4 刀轴矢量拐角光顺误差控制示意图

图4中:e为构造PH曲线的控制误差;ε为PH曲线中点E在单位圆上投影的方向误差。根据1.1节PH曲线构造方法,曲线误差度量为长度,而刀轴矢量光顺误差为角度,因此需对其进行转换,将角度误差ε转换为长度误差e进而构造PH曲线。下面给出转化过程:

(10)

根据(10)式可得:

(11)

由(10)式可知,e与ε在[0,π/2]内成正相关,当给定刀轴矢量误差上限ε时,根据(11)式获得构造PH曲线的控制误差上限e。据此可以得到误差均在允许范围内的光顺刀轴矢量。

2 参数同步

五轴机床刀尖点和刀轴方向相互独立,实现刀尖点和刀轴方向子轨迹运动同步是五轴线性路径拐角光顺的另一个难点。若直接采用线性同步，则会导致直线段和曲线段的衔接点处刀轴矢量突变。为此,本文通过调整光顺曲线控制点使刀轴矢量的几何导数在直线和曲线衔接点处连续,然后使用线性同步的方法使刀尖点和刀轴矢量同步,这样可以有效实现五轴机床刀尖点和刀轴方向运动同步且避免刀轴矢量运动突变。

为保证光顺后刀轴矢量在过渡曲线和原始轨迹的衔接处一阶和二阶导数连续,PH曲线控制点应满足如下关系式:

(12)

其中：oi-1、oi+1分别为Oi-1、Oi+1点矢量;pi-1、pi+1分别为Pi-1、Pi+1点矢量，下文同。

参数同步示意图如图5所示。

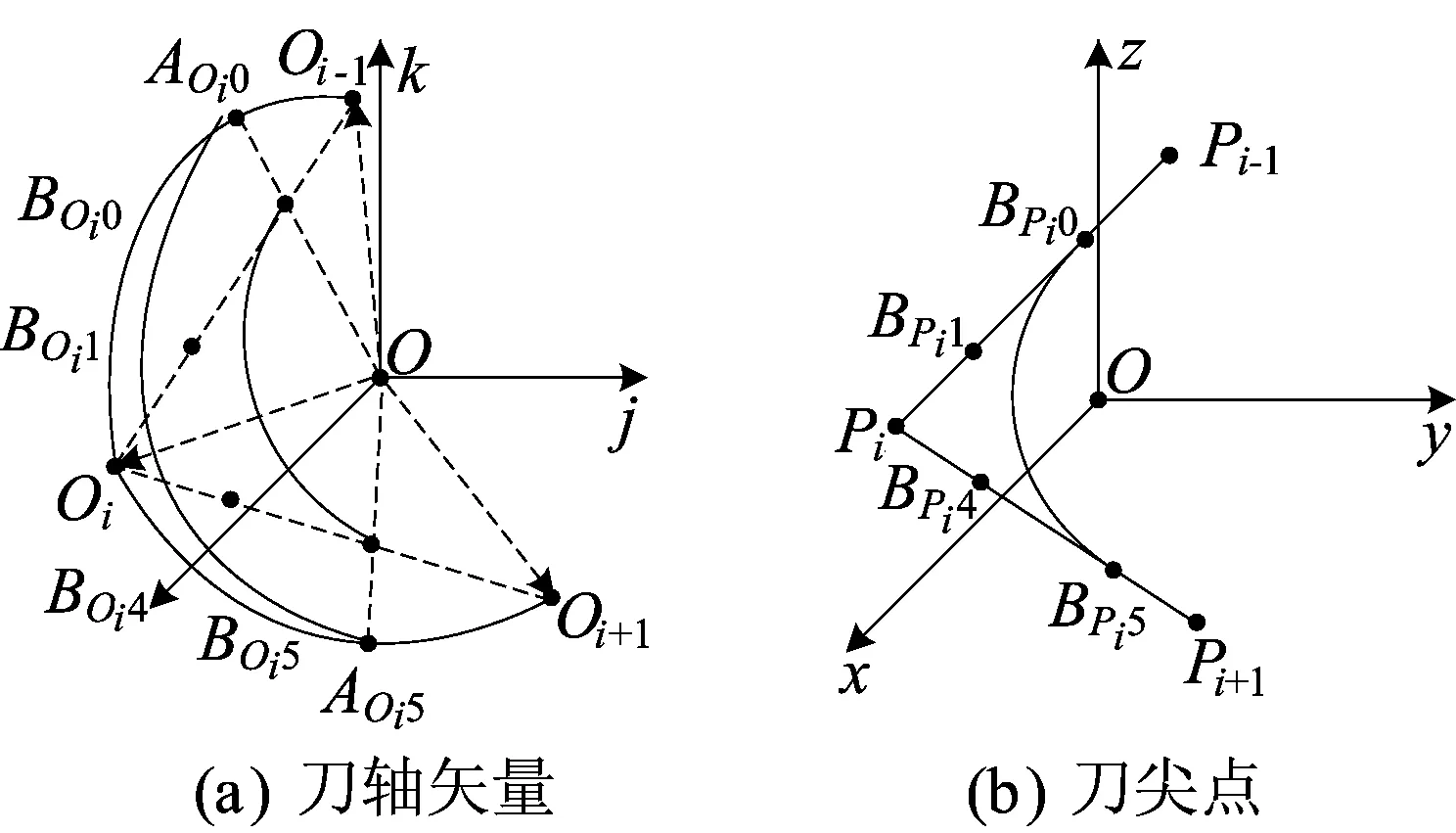
图5 参数同步示意图

下面结合图5给出(12)式的证明。

设O(u)为刀轴矢量的轨迹曲线,P(u)为刀尖点轨迹曲线,u为曲线参数且u∈[0,1],s为刀具路径长度。五轴刀具路径任意点处刀轴矢量的一阶导数可表示为:

(13)

其中

(14)

在原始直线段中,原始直线段与过渡曲线“入口”衔接处u=1,即在AOi0处u=1,将u值带入(13)式可得:

(15)

在过渡曲线中,原始直线段与过渡曲线“入口”衔接处u=0,即在AOi0处u=0,结合(1)式和(14)式可得:

(16)

(17)

将(16)式、(17)式带入(13)式可得:

(18)

刀轴矢量在原始直线段和过渡曲线段的“入口”衔接处一阶导数连续应满足(15)式与(18)式相等，即可得到(12)式中的第1式。同理,当刀轴矢量在原始直线段和过渡曲线段的“出口”衔接处,即AOi5点处一阶导数连续时可得(12)式中的第2式。

五轴刀具路径任意点处刀轴矢量的二阶导数可表示为:

(19)

其中

(20)

在过渡曲线中,AOi0处u=0,结合(1)式、(9)式、(14)式和(20)式可得:

(21)

(22)

将(16)式、(17)式、(21)式和(22)式代入(19)式可得:

(23)

在原始直线中AOi0处u=1,刀轴矢量二阶导数为0,由此可得刀轴矢量在原始直线段和过渡曲线段的“入口”衔接处二阶导数连续,同理可得刀轴矢量在原始直线段和过渡曲线段“出口”衔接处二阶导数连续。综上所述,(12)式得证。

综上,刀轴矢量光顺可分为2步:

(1) 采用1.3节所述方法将光顺后刀轴矢量投影到单位球面上以获得单位化刀轴矢量。

(2) 采用本节所述方法调整刀轴矢量过渡曲线控制点,使光顺后刀轴矢量轨迹在原始直线段和过渡曲线段的衔接处几何连续并与刀尖点光顺轨迹参数同步。

3 仿真分析

本节采用仿真的方法验证本文所提算法的正确性。首先对随机生成的刀位点进行光顺处理,验证算法的计算效率和刀轴矢量误差控制效果;然后通过一个双拐角五轴刀具路径验证算法同步的正确性。

3.1 计算效率与误差控制效果比较

将本文所提光顺方法与对比方法[14]进行计算效率比较,验证计算本文方法在刀轴矢量误差控制方面的控制效果。为实现计算效率的比较,首先在工件坐标系下随机生成一定数量的刀位点,通过对上述随机生成的刀位点进行光顺,比较2种方法的计算时间。关于刀轴矢量误差控制效果的比较,首先在工件坐标系下随机生成2 000个刀位点,然后对所生成的刀位点进行光顺处理。给定刀轴矢量光顺误差ε*=0.4°,实际刀轴矢量误差定义为ε。通过ε与ε*的比值来判断本文方法刀轴矢量误差的控制效果。ε/ε*的值越接近1说明控制效果越好。

随机生成的不同数量刀位点光顺后的平均时间(CPU基准频率3.6 GHz,RAM 16 GiB)如图6所示。由图6可知,本文方法比对比方法的计算效率提升了30%左右。2种方法刀轴矢量误差及误差比值如图7所示。由图7可知:对比方法中刀轴矢量误差平均值为0.386 5°,是给定值(0.4°)的96.625%;且ε/ε*的平均值为96.15%。本文方法中刀轴矢量误差平均值为0.383 2°,是给定值(0.4°)的95.8%,且ε/ε*的平均值为96.28%。由此可以看出,本文五轴刀具路径拐角光顺方法相较于对比方法在刀轴矢量误差控制效果相近的情况下具有更高的计算效率。

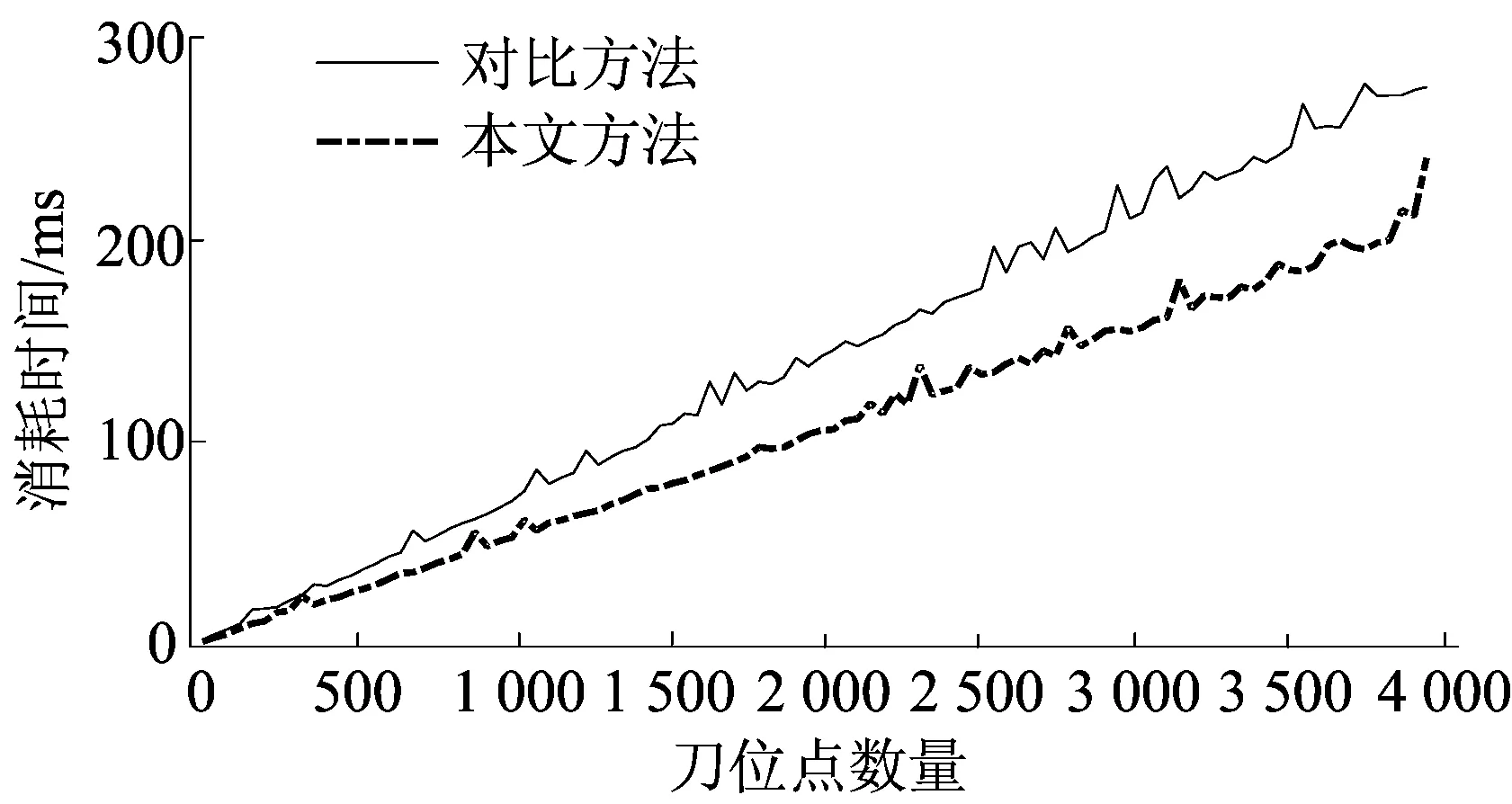
图6 2种方法计算耗时

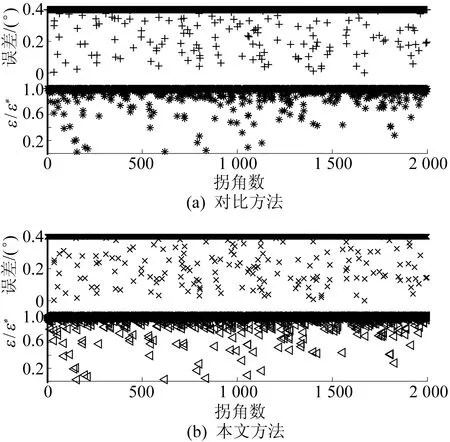
图7 2种方法刀轴矢量误差及误差比值

3.2 五轴转接光顺仿真

根据对比方法中所用的双拐角五轴刀具路径验证本文方法生成轨迹的光顺性,光顺后刀具路径如图8所示。

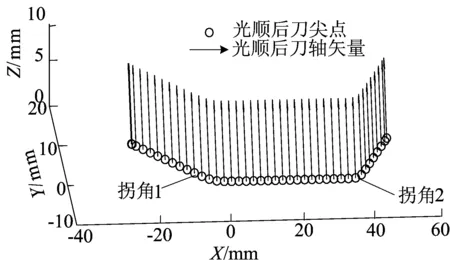
图8 光顺后刀具路径

使用2种方法对双拐角路径进行100次光顺处理,平均耗费时间见表1所列。本文方法平均耗时比对比方法平均耗时缩短了24%，可有效提高光顺效率。

光顺后拟合误差如图9所示。

由图9可知,刀尖点和刀轴矢量误差均在允许范围内,说明了本文拐角光顺路径生成算法的正确性。

表1 2种方法平均耗时

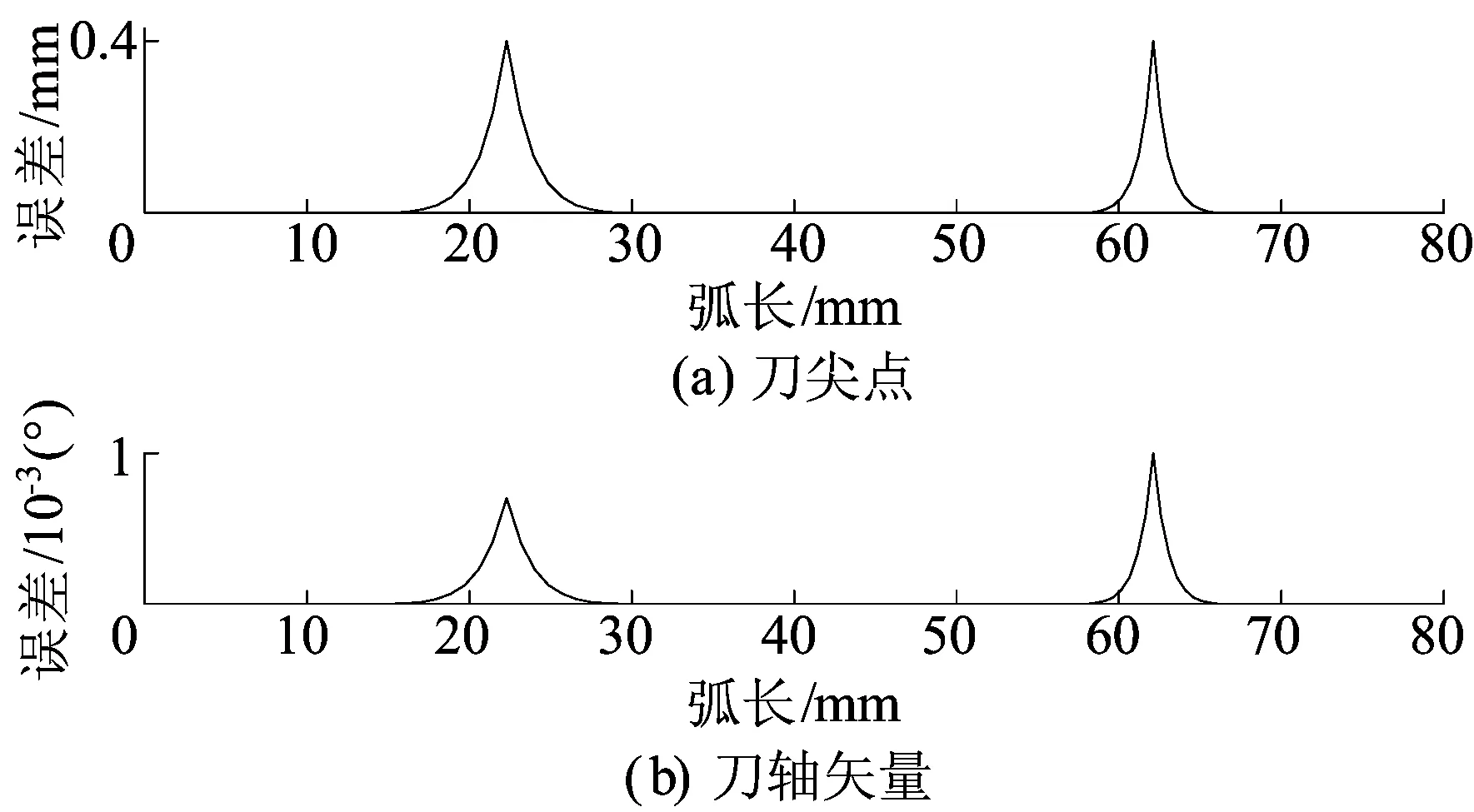
图9 拟合误差

线性路径和光顺后路径刀尖点速度和刀轴矢量角速度如图10所示。线性路径加工时间为4.667 s,光顺后路径加工时间为4.085 s,加工效率提升了12.5%。在2个拐角处刀轴矢量角速度同步前有明显的突变,突变造成机床各驱动轴的运动不连续,产生冲击和明显运动误差,而同步后刀轴矢量角速度连续变化,可有效避免上述问题。

同步前后刀轴矢量角加速度如图11所示。由图11可知,刀具在通过拐角1时,刀轴矢量角加速度由同步前的-4.739 (°)/s2降低到同步后的-0.027 54 (°)/s2,在拐角2处,刀轴矢量角加速度的最大突变由同步前的5.916 (°)/s2降低到同步后的0.029 91 (°)/s2。由此可见,参数同步算法显著降低了刀轴矢量在拐角处角速度和角加速度的波动。

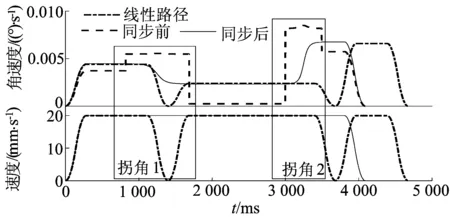
图10 线性路径和光顺后刀尖点速度及刀轴角速度

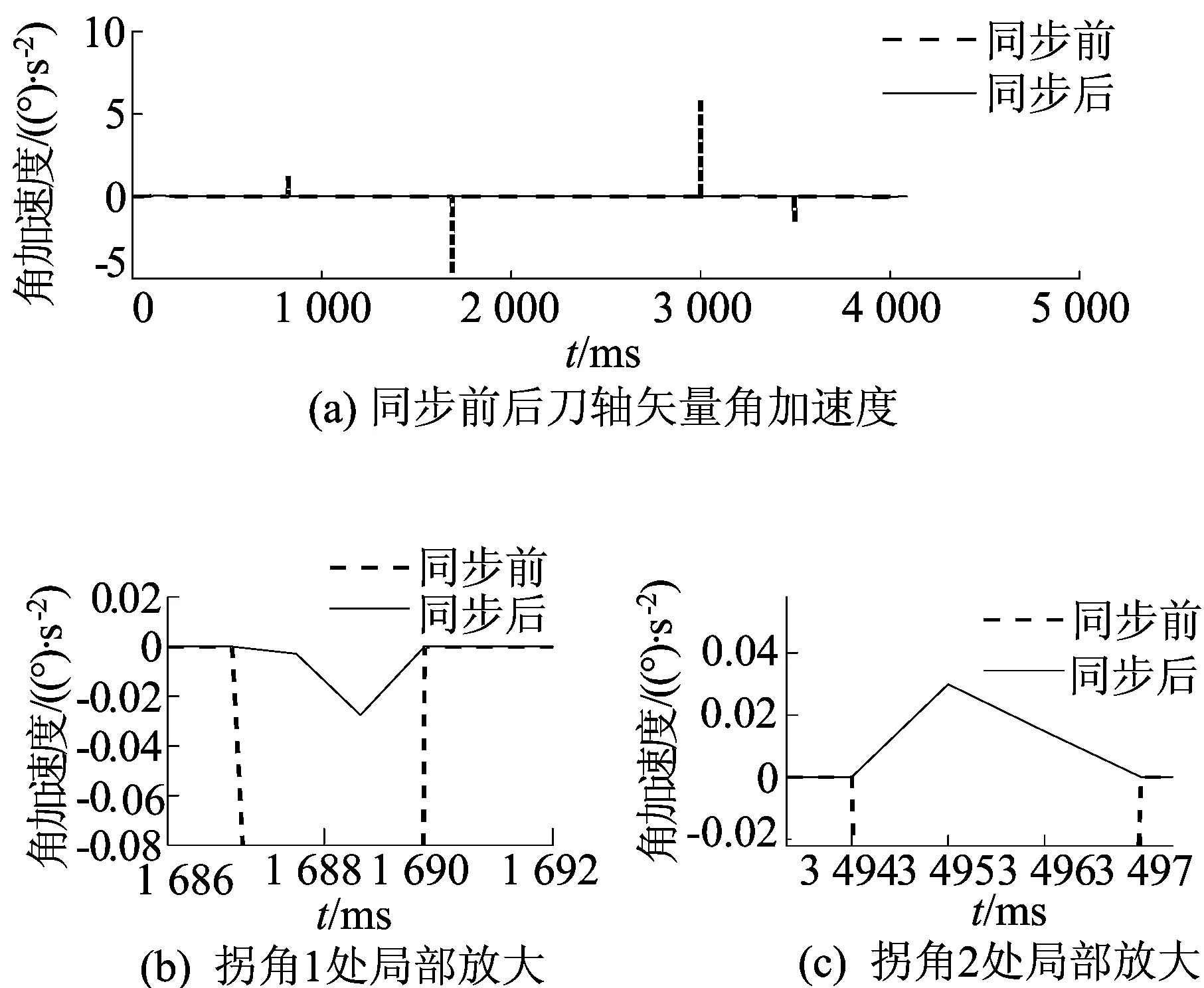
图11 同步前、后刀轴矢量角加速度

根据文献[20]中搭建的AC型五轴数控机床,对同步前、后的刀位数据进行逆解，得到各运动轴的变化量如图12所示。

从图12可以看出,同步后各轴变化平缓,尤其是X轴和C轴变化最明显,降低了机床冲击。

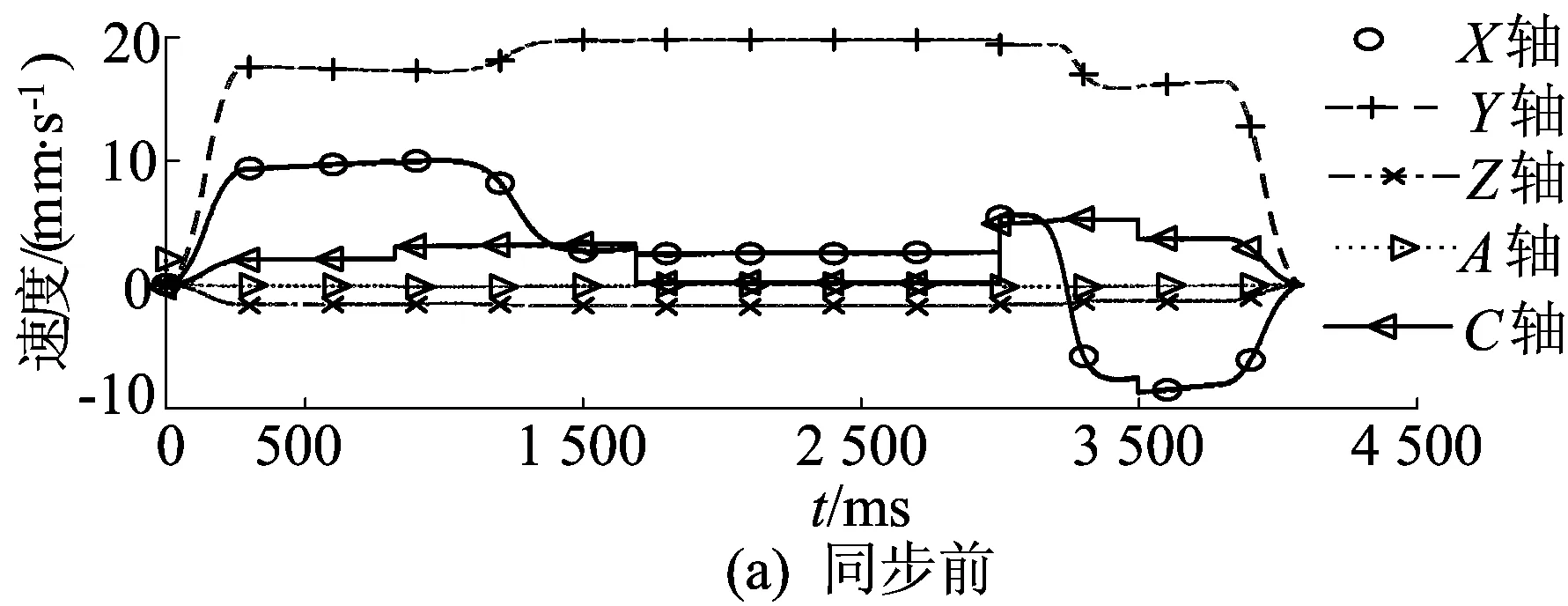
图12 同步前、后各运动轴的变化量

4 结 论

(1) 本文提出一种基于双五次PH曲线的五轴线性路径拐角光顺解析算法,光顺轨迹满足G2连续性要求且过渡曲线弧长和参数具有解析表达式,有利于以弧长为要素的五轴光顺曲线参数插补。

(2) 五轴线性路径刀尖点和刀轴矢量近似误差在工件坐标系下解析可控，尤其是刀轴矢量误差具有较好的控制效果,且计算效率高。通过基于线性同步机制调整控制点策略,实现了过渡曲线与原始直线在衔接点处刀轴矢量平稳过渡。

(3) 仿真结果表明,本文方法能保证刀尖点和刀轴矢量误差在允许范围内且计算效率高,同步光顺后相较于未同步光顺各运动轴变化平稳,有利于将本文算法集成到数控系统中实现五轴轨迹在线光顺。