基于演化模式的推特话题流行度预测方法
解伟凡,郭岩*,匡广生,余智华,薛源海,沈华伟
基于演化模式的推特话题流行度预测方法
解伟凡1,2,郭岩1*,匡广生1,3,余智华1,薛源海1,沈华伟1
(1.中国科学院计算技术研究所 数据智能系统研究中心,北京 100190; 2.中国科学院大学 计算机科学与技术学院,北京 101408; 3.中国科学院大学 人工智能学院,北京 101408)(∗通信作者电子邮箱guoy@ict.ac.cn)
针对以往流行度预测方法未利用演化模式之间的差异和忽略预测时效性的问题,提出了一种基于演化模式的推特话题流行度预测方法。首先,基于‑SC算法对大量历史话题的流行度序列进行聚类,并得到6类演化模式;然后,使用各类演化模式下的历史话题数据分别训练全连接网络(FCN)作为预测模型;最后,为选择待预测话题的预测模型,提出幅度对齐的动态时间规整(AADTW)算法来计算待预测话题的已知流行度序列与各演化模式的相似度,并选取相似度最高的演化模式的预测模型进行流行度预测。在根据已知前20 h的流行度预测后5 h的流行度的任务中,与差分整合移动平均自回归(ARIMA)方法以及使用单一的全连接网络进行预测的方法相比,所提方法的预测结果的平均绝对百分比误差(MAPE)分别降低了58.2%和31.0%。实验结果表明,基于演化模式得到的模型群相较于单一模型能更加准确地预测推特话题流行度。
推特话题;演化模式;流行度预测;社交网络;时间序列
0 引言
随着互联网技术的不断发展,社交网络已经成为人们日常生活中不可或缺的一部分。社交网络的出现,极大地方便了消息的产生和传播。在社交网络上,用户针对自己感兴趣的话题发布消息,备受关注的热点话题会迅速扩散,具体表现包括消息发布数量大、消息的转发评论次数多、消息发布者的社会影响力大等。网络话题的流行度预测有着重大的现实意义,在话题传播早期预测出下一阶段的流行程度,可以对话题在将来是否成为热点话题进行及时的预判,在舆情监控、流量分发、话题推送、网络营销等领域有重大的应用价值。推特平台的话题以Hashtag形式呈现,受到人为干预程度较低,是流行度预测的合适对象。
已有的流行度预测方法的处理对象集中在消息级别,而话题级别的流行度预测研究相对匮乏。同时,流行度预测往往有时效要求,意味着待预测话题的观测窗口较小,仅能使用早期极其有限的流行度数据。相应地,与待预测话题同属一类演化模式的历史话题经历了完整的生命周期,观测窗口较大,流行度数据相对完备。充分利用与待预测话题具有相同流行度演化模式的历史话题数据,可以有效弥补待预测话题数据量较少对预测产生的干扰。已有的研究仅使用待预测话题本身的数据进行预测,或者将全部历史话题纳入单一的预测模型,忽略了不同历史话题与待预测话题在演化模式的相似程度上存在差异,未充分利用待预测话题同属一类演化模式的历史话题数据,这些不足都影响了预测效果。
本文提出了一种基于演化模式的推特话题流行度预测方法,先进行历史话题的聚类,得到各类演化模式并训练对应的预测模型,然后判断待预测话题的演化模式,最后基于该模式的预测模型进行流行度预测。本文使用小时内与话题相关的消息发布数量作为流行度。为了得到反映大部分推特话题的流行度变化趋势且彼此存在明显差异的一组演化模式,本文基于历史话题在时序上完整的流行度序列,采用Yang等[1]提出的‑SC(‑Spectral Centroid)聚类算法生成各类别的中心作为话题级别的流行度演化模式,同时得到每类模式下包含的历史话题,对每个演化模式单独训练预测模型。对于待预测的话题,本文根据早期的流行度数据进行演化模式级别的分类,以待预测话题的已知流行度序列与基于历史话题数据生成的各个演化模式的序列距离作为分类依据。考虑到‑SC算法只能计算长度相等的序列之间的距离,而待预测话题的已知流行度序列与基于历史话题数据生成的演化模式是一对长度不等的序列,本文提出基于幅度对齐的动态时间规整(Amplitude‑Alignment Dynamic Time Warping, AADTW)算法计算待预测话题的已知流行度序列与各演化模式的距离,以与其距离最小的类别下的预测模型进行流行度预测。在实验中,本文的方法与完全不使用历史话题数据的方法、使用全部历史话题训练单一预测模型的方法分别进行了对比,结果表明本文方法取得了更优的效果。
本文主要工作如下:
1)提出基于演化模式的推特话题流行度预测框架。该框架在离线阶段挖掘历史话题的流行度演化模式,并训练对应的预测模型;在线阶段根据待预测话题的早期数据,将其分到演化模式相似的类别中,并使用相应的预测模型预测其流行度。该框架的优点是:对于待预测话题,仅需其早期流行度序列作为输入,无需非时序数据,很好地适应了流行度预测问题对时效性要求,解决了待预测话题早期数据少的问题。
2)提出基于幅度对齐的动态时间规整(AADTW)算法。朴素的动态时间规整(Dynamic Time Warping, DTW)[2]算法虽然提供了变长序列之间距离的定义,能够较好地适应历史话题的演化模式与待预测话题的已知流行度序列在长度上存在的差异,但是该距离定义没有充分强调一对序列在时序上的变化趋势的相似程度,会对待预测话题的演化模式做出错误的判断。针对该问题,本文提出AADTW算法,该算法通过引入‑SC算法计算等长序列之间的距离时采用的幅度对齐思想,并结合DTW算法处理变长序列的时序拉伸思想,更好地解决了判断待预测话题的演化模式这一问题。
1 相关工作
1.1 消息级别的流行度预测
从消息级别的流行度预测方法中可以发现,有必要引入消息级别或话题级别的相似度计算方法,据此对待预测的消息或话题进行分类,按类别分别训练预测模型,这样可以对不同话题进行更具针对性的流行度预测,避免噪声数据对预测产生干扰。
1.2 话题级别的流行度预测
话题级别的流行度预测的已有工作相对较少。Hu等[14]分析了若干突发话题在社交网络的流行度随时间变化的周期性,发现其中包含间隔较短的多个峰值,提出了一种基于Holt‑Winters模型的话题级别的流行度预测方法,仅使用待预测话题早期的评论间隔数据。Li等[15]提出了一种基于情感强度的话题级别流行度预测方法,将话题相关的发文量作为流行度量化指标,对大量用户特定话题下消息的情感表达数据和流行度数据进行特征融合,结合差分整合移动平均自回归(Auto‑Regressive Integrated Moving Average, ARIMA)方法预测话题在将来一段时间的流行度,效果优于不引入情感特征的方法。Wang等[16]同样考虑到情感强度在话题级别流行度预测中的作用,结合Markov随机场对流行度进行预测,效果优于不引入情感特征的方法。Gupta等[17]设计了多个流行度量化指标,根据文本特征等非时序特征对话题进行分类,训练多个模型进行预测,并验证了指标设计的合理性。王新乐等[18]使用推特平台和微博平台的Hashtag的内容主题特征、时间特征、序列特征、用户粉丝网络特征等进行基于支持向量机的主题标签的流行度预测,但该方法需要大量的非时序数据支撑,获取的时间成本较高。
以往的话题级别流行度预测方法或者忽略了历史话题数据的作用,仅使用待预测话题自身的数据进行预测;或者将历史话题的数据集中训练单一预测模型,未考虑到某些历史话题的流行度演化模式与待预测话题不同,在训练数据中作为干扰噪声存在,影响预测效果,而那些演化模式与待预测话题相似的历史话题却未被重视;或者考虑到了对不同类别下的话题分别训练预测模型,但是需要大量的非时序数据作为支持,获取数据的时间成本较高,忽略了预测的时效性要求。
2 本文模型
2.1 问题形式化
2.2 整体预测框架
本文方法首先根据流行度演化模式对历史话题进行聚类,得到各个话题类别中心以及历史话题的类别标签;然后使用每个话题类别的数据训练该类的预测模型,各话题类别的预测模型构成了模型群。对于每个待预测话题,计算其早期的流行度序列与各话题类别中心的相似度,将待预测话题路由至与其相似度最高的话题类别下的预测模型进行流行度预测。整体框架如图1所示。
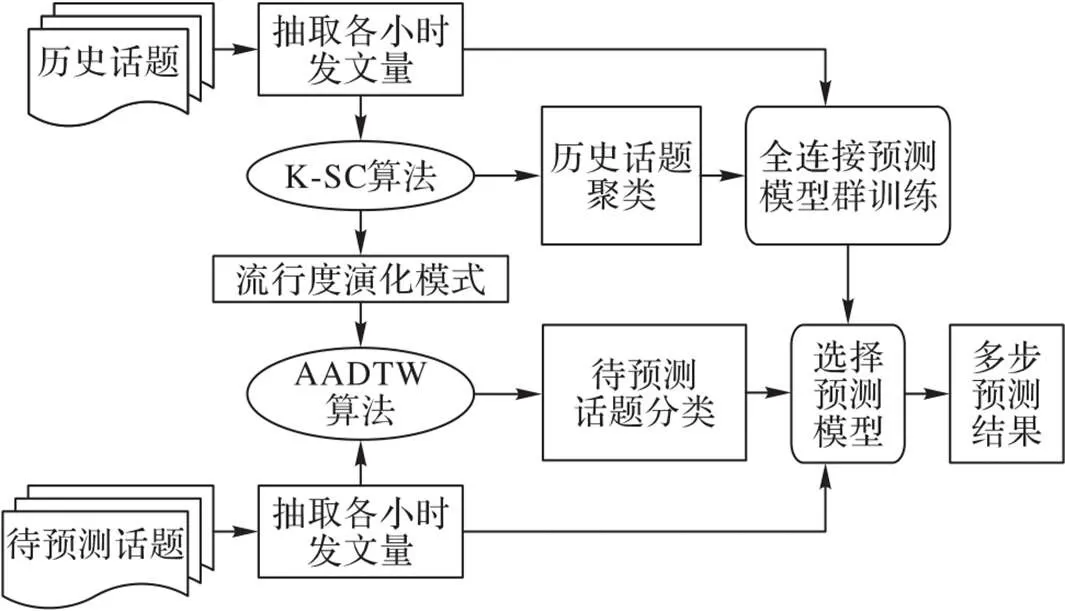
图1 整体预测框架
预测框架可以分为以下三个模块:
1)历史话题的聚类模块:功能为离线挖掘历史话题的流行度演化模式,并根据演化模式对话题进行分类。实际场景中能获得历史话题整个生命周期中的流行度序列,可以设置较大的观测窗口,故各历史话题序列长度相等且较大。问题抽象为计算长度相等的时间序列之间的距离,Yang等[1]的工作证明‑SC算法可以很好地解决该问题,因此本文基于‑SC算法建立此模块。
2)预测话题的分类模块:功能为根据待预测话题的早期数据,判断话题的演化模式类别。由于观测窗口通常较小,因此待预测话题的早期流行度序列较短,而历史话题的聚类模块得到的各类别中心的序列通常较长,需要计算两个不等长序列之间的距离,序列距离是待预测话题分类的唯一根据。问题抽象为计算长度存在较大差别的时间序列之间的距离,且距离定义应当充分体现序列在演化模式上的差异。DTW算法的序列距离定义较好地适应了序列之间长度不相等的情况,但是受到序列间的幅度差异、演化模式上的差异等诸多因素影响,直接使用该距离定义会使部分待预测话题没有选择与其在变化趋势上最相似的类别中心作为自身的演化模式,而是错误地选择与其在幅度上最接近的类别中心作为自身的演化模式。针对该问题,本文提出了AADTW算法以建立待预测话题分类模块。
3)预测模块:功能包括两个阶段,即离线为每个类别训练预测模型,以及在线为待预测话题预测其流行度。各个类别的预测模型之间结构相同,区别在于训练数据不同导致参数不同。本文基于全连接神经网络建立预测模块。
2.3 基于K‑SC算法的历史话题聚类模块
聚类模块的输入是若干历史话题的流行度序列,聚类算法将在观测窗口内流行度变化趋势相似的历史话题归入同一类别,输出包括:
1)各个历史话题所属的唯一的类别标签,根据该标签确定每个类别的预测模型的训练集;
2)各个类别的中心,每个类别中心代表一类演化模式,要直观表现类内所有流行度序列在变化趋势上的共同点,同时要淡化类内不同流行度序列在幅度上的差异。
‑SC算法的执行流程与K‑Means算法类似,是多阶段迭代的过程,在每个阶段首先尝试逐个更新序列所属的类别,然后重新计算各个类别的中心,直至所有序列的类别保持不变。
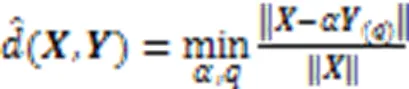
K‑Means算法将类别内全体样本的均值作为类别中心,不能在时间序列聚类中沿用,因为这种定义中心的方法与使用欧几里得距离进行相似度计算的方法一样,淡化了序列的演化模式,过分强调序列之间的幅度区别和细微延迟引发的差异。‑SC算法设计了新的类别中心:
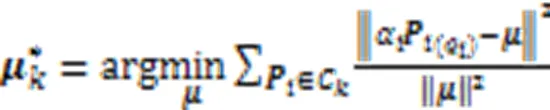
2.4 基于AADTW算法的待预测话题分类模块
此模块将判断待预测话题的演化模式这一问题转化为多分类问题,以预测话题的已知流行度序列与基于历史话题数据生成的各个演化模式的序列距离作为分类依据。历史话题经历了从产生到消亡的完整生命周期,其流行度序列与待预测话题早期数据构建的流行度序列在长度上存在明显差异,如何定义和计算长度不同的序列之间的距离?针对该问题,本文提出了一种基于幅度对齐的动态时间规整算法,对待预测话题进行演化模式级别的分类。朴素的DTW算法虽然能够较好地适应序列之间的长度差异,但直接使用可能会得到待预测序列与趋势不同的演化模式存在最小的序列距离,导致分类结果错误。
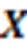
1)状态为当前取出的两个子序列各自的长度。
2)阶段为两个子序列的长度之和。在问题求解的过程中,两个子序列的长度都是单调不减的,保证了子问题的无后效性。
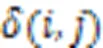
综上所述,状态转移方程为:
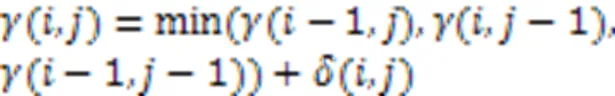
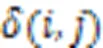
针对以上问题,引入‑SC算法中的伸缩度概念,重新定义不等长序列之间的距离,提出AADTW算法。
图2以一个在观测窗口中经历多次流行度峰值的待预测话题为例,展示了AADTW算法与DTW算法的区别。模式A代表在生命周期中经历单个流行度峰值的一类话题,模式B代表在生命周期中经过多个流行度峰值的一类话题。待预测话题的流行度曲线在观测窗口内已经经历一次完整的波峰,并且即将到达新的波峰,从流行度变化趋势的角度应当归入模式B。图2(a)中可以看到模式A与待预测话题的流行度曲线逼近程度较高,二者均偏离模式B的曲线,朴素DTW算法计算出的结果是模式A与待预测话题的距离更接近,会错误地将待预测话题归入模式A。图2(b)中AADTW算法对模式A进行了幅度压缩,对模式B进行了幅度拉伸,目的均是使二者的曲线尽可能逼近待预测话题,经过幅度对齐的处理后,AADTW算法计算的结果是待预测话题与模式B更接近。
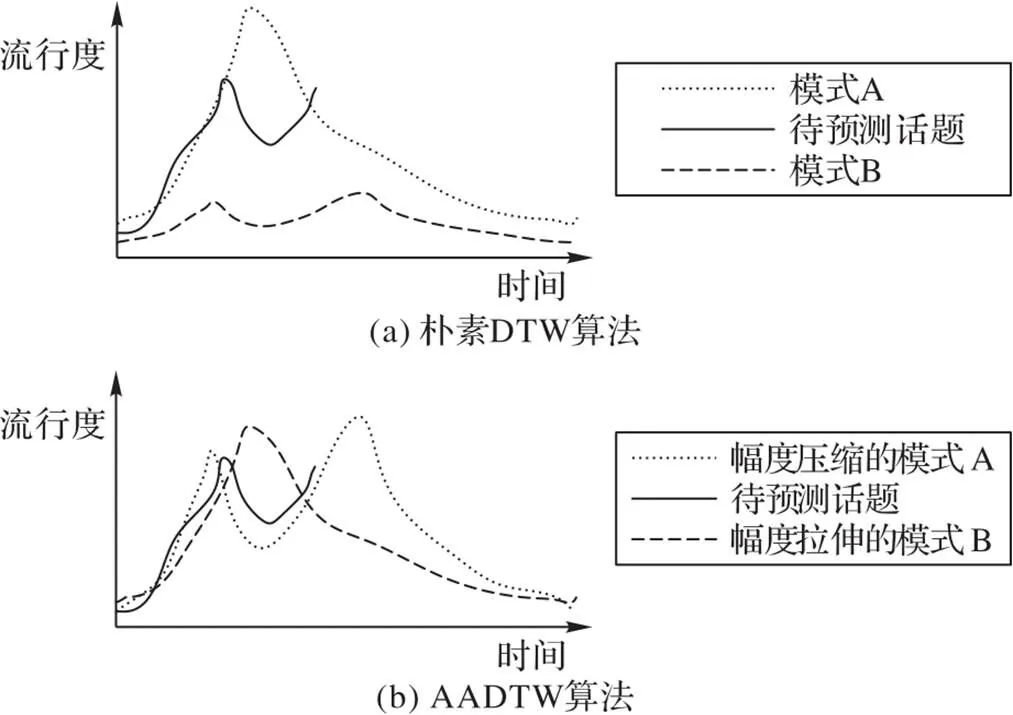
图2 DTW算法与AADTW算法对观测窗口内存在多峰的待预测话题进行分类时的区别
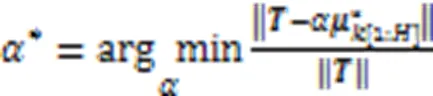

2.5 基于全连接网络群的预测模块
本文使用全连接网络(Fully Connected Network, FCN)进行时间序列的多步预测,网络结构包括输入层、隐藏层、输出层。其中:输入层的输入长度等于待预测话题的观测窗口,输出层的输出长度为预测窗口。使用每个话题类别包含的流行度数据训练该类别的全连接预测网络,各类别对应的网络结构相同,区别在于参数,共同构成一个网络群,选择平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)作为损失函数实验数据。
Yang等[1]分析了推特上1 000个Hashtag从首次出现起各小时内被提及次数,发现对于大部分话题Hashtag,用户的发文行为基本集中在前128 h,所以本文设置采集时间为128 h。多数Hashtag在第50 h前后会经历小时内被提及次数的峰值,之后的流行度变化幅度明显小于前50 h内,即50 h后话题的传播规模趋于稳定,从时效性考虑,观测窗口在50 h内流行度预测更有意义,所以实验中设置的观测窗口均在50 h以内。话题的流行度在20 h内基本处于不断增长的状态,难以从中发现演化模式的差异,所以实验中设置的观测窗口至少为20 h。本文采集了推特平台上7.5万个话题Hashtag前128 h内的发文数据,按小时切分后得到各小时的发文量。选取其中90%的话题Hashtag作为训练集,其余10%话题Hashtag作为测试集。测试的观测窗口分别为20 h、30 h、40 h,预测窗口始终为5 h。注意到测试设置的观测窗口的长度远小于采集数据的完整时间区间,这是为了模拟实际预测场景下已知待预测话题的少量数据和各历史话题的完整时序数据。
3 实验与结果分析
3.1 实验设置
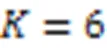
1)ARIMA模型:仅使用待预测话题本身的数据进行预测,完全不使用历史数据。
2)单一的FCN模型:使用全部训练数据训练一个全连接网络,所有的测试数据均使用该模型进行预测。
3)复用‑SC算法建立分类模块的模型(‑SC+FCN):对训练数据使用‑SC算法进行聚类后,采取将各话题类别中心进行裁剪尾部的处理,保留长度等于观测窗口的前缀,使用‑SC算法的距离定义计算其与测试数据的序列距离,选择与测试数据距离最小的一类作为测试数据的类别。
4)使用朴素DTW算法建立分类模块的模型(‑SC+DTW+FCN):对训练数据使用‑SC算法进行聚类后,使用DTW算法计算测试数据与各话题类别中心的距离,选择与测试数据距离最小的一类作为测试数据的类别。
为验证本文方法的稳定性,还根据待预测话题的分类结果,以及流行度预测结果计算每类演化模式下的MAPE。
3.2 结果与分析
本文使用MAPE作为预测结果的评价指标,该指标的计算方法为:
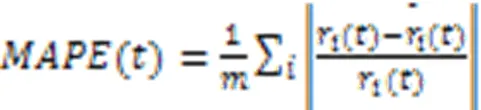

表1 不同模型的MAPE
从表1可以发现,本文方法(‑SC+AADTW+FCN)在各观测窗口下均取得了最优的效果,下面依次对各组实验进行分析:
1)ARIMA:ARIMA模型的MAPE始终大于1,预测结果存在严重失真,ARIMA模型仅基于待预测话题已有的数据进行预测,而且假设序列具有周期性,实际上话题传播的演化模式并不具有明显的周期性,违背了ARIMA的假设。验证了在观测窗口较小的情况下,仅使用待预测话题的已知流行度对后续流行度预测难以取得理想效果。
2)FCN:一方面,FCN模型相较于ARIMA有明显的性能提升,验证了引入历史话题数据的必要性;另一方面,FCN模型的表现相较于使用‑SC算法进行历史话题聚类的后两种方法存在差距。使用单一预测模型实际上将所有历史话题的数据置于同等的地位,没有发现历史话题流行度演化模式存在的明显差异,与待预测话题的演化模式不同的历史话题成为噪声,对预测形成干扰。这说明引入‑SC算法可以发现相似话题,历史的相似话题在流行度预测中发挥重要作用。
3)‑SC+FCN:使用KSC算法同时完成历史话题聚类和待预测话题分类的方法,其预测效果随着观测窗口增大有最明显提升,验证了KSC算法能起到过滤历史话题数据、保留演化模式与待预测话题相似的历史话题的作用。
4)‑SC+DTW+FCN:一方面,在待预测话题分类模块使用朴素DTW算法使得预测效果相较于使用‑SC算法有了进一步的提升,验证了DTW算法能够更好地量化长度存在明显差异的时间序列之间的相似程度。另一方面,相较于上一种方法(‑SC+FCN)的预测效果提升程度随着观测窗口增大不断缩小。这是因为文献[1]发现推特话题的流行度演化模式在话题首次出现后接近50 h基本可被确定,而本文设置的观测窗口越来越接近50 h。换言之,越是在话题出现的早期,观测窗口越小,DTW算法相较于‑SC算法在待预测话题分类任务上的优势越明显。
5)‑SC+AADTW+FC:本文提出的AADTW算法在计算序列之间的距离时同时具备‑SC算法抵消序列之间的幅度差异,以及DTW算法适应序列之间长度差异的特点,使得序列之间演化模式的相似程度成为影响序列距离的主要因素,在流行度预测问题上充分利用了历史话题的演化模式。基于AADTW算法建立待预测话题分类模块,相较于使用朴素DTW算法进一步提高了预测效果。与ARIMA和FCN相比,本文方法的MAPE分别降低了58.2%和31.0%
本文还根据待预测话题的分类结果,以及流行度预测结果计算每类演化模式下的MAPE,结果见表2。可以发现,在每个观测窗口下,每类演化模式的MAPE与测试集整体的MAPE十分接近,表明本文的方法对不同的待预测话题进行预测时具有稳定的表现。
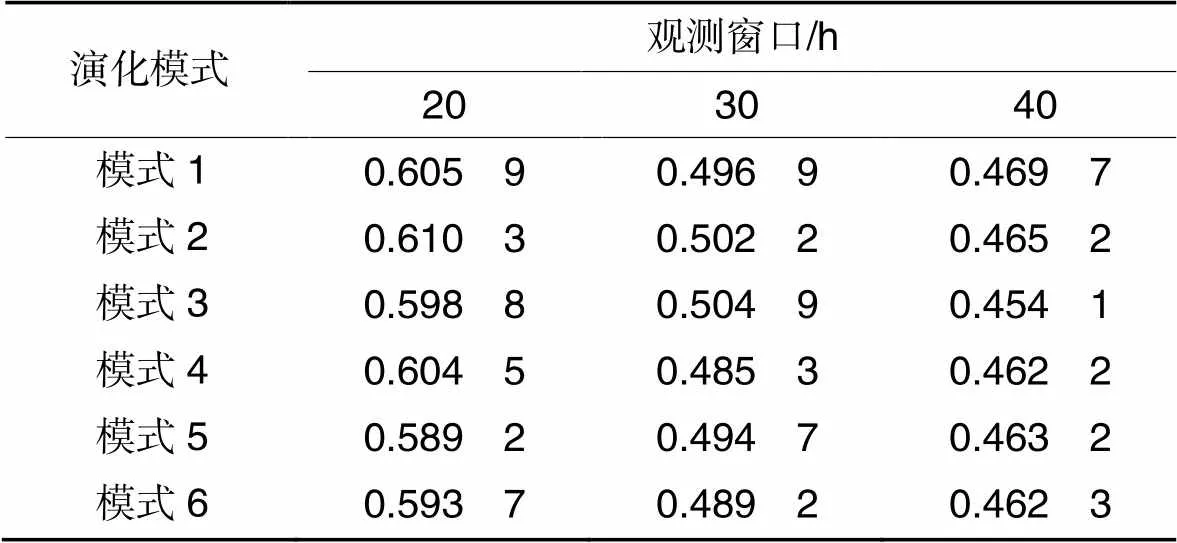
表2 不同演化模式的MAPE
4 结语
话题级别的流行度预测问题有时效要求,在话题出现早期存在流行度数据不足的问题,历史话题的数据相对完备,考虑使用与待预测话题的流行度演化模式相似的历史话题数据提高预测效果。本文提出一种基于演化模式相似的历史话题进行流行度预测的方法。通过一系列的对比试验,验证了该方法的有效性。本文方法与完全基于待预测话题自身数据的ARIMA模型相比,验证了引入历史数据可以显著降低早期流行度预测的误差;与使用全部历史话题数据训练单一预测模型的方法对比,验证了引入‑SC聚类算法可以有效过滤对预测任务产生干扰的历史事件;与使用‑SC算法做待预测话题分类的方法对比,验证了在话题出现早期数据不足的情况下,引入DTW算法可以明显提高待预测话题分类效果;与使用朴素DTW算法进行待预测话题分类的方法对比,验证了AADTW算法相较DTW算法能更好地判断待预测话题的演化模式,进而提高预测效果。本文计算了每类演化模式下的MAPE,验证了方法的稳定性。
在本文的流行度预测方法中,仅使用了话题的部分时序特征,未来可以考虑结合话题的非时序特征,例如话题的情感色彩等。在计算时间序列之间的变化趋势的相似度问题上,可以考虑使用其他的幅度对齐方法,或者使用其他的计算变长序列距离的算法以更好地解决问题。
[1] YANG J, LESKOVEC J. Patterns of temporal variation in online media[C]// Proceedings of the 4th ACM International Conference on Web Search and Web Data Mining. New York: ACM, 2011:177-186.
[2] BERNDT D J, CLIFFORD J. Using dynamic time warping to find patterns in time series[C]// Proceedings of the 1994 AAAI Conference on Knowledge Discovery and Data Mining. Menlo Park, CA: AAAI Press, 1994:359-370.
[3] SZABO G, HUBERMAN B A. Predicting the popularity of online content[J]. Communication of the ACM, 2010, 53(8):80-88.
[4] 朱海龙,云晓春,韩志帅. 基于传播加速度的微博流行度预测方法[J]. 计算机研究与发展, 2018, 55(6):1282-1293.(ZHU H L, YUN X C, HAN Z S. Weibo popularity prediction method based on propagation acceleration[J]. Journal of Computer Research and Development, 2018, 55(6):1282-1293.)
[5] BAO P, SHEN H W, HUANG J M, et al. Popularity prediction in microblogging network: a case study on Sina Weibo[C]// Proceedings of the 22nd International Conference on World Wide Web. New York: ACM, 2013:177-178.
[6] 高金华,沈华伟,程学旗,等. 基于相似消息的流行度预测方法[J]. 中文信息学报, 2018, 32(11):79-85.(GAO J H, SHEN H W, CHENG X Q, et al. Popularity prediction method based on similar historical tweets[J] Journal of Chinese Information Processing, 2018, 32(11):79-85.)
[7] WANG X M, FANG B X, ZHANG H L, et al. Predicting the popularity of news based on competitive matrix[C]// Proceedings of the IEEE 2nd International Conference on Data Science in Cyberspace. Piscataway: IEEE, 2017:151-155.
[8] AHMED M, SPAGNA S, HUICI F, et al. A peek into the future: predicting the evolution of popularity in user generated content[C]// Proceedings of the 6th ACM International Conference on Web Search and Data Mining. New York: ACM, 2013:607-616.
[9] LYMPEROPOULOS I N. RC‑Tweet: modeling and predicting the popularity of tweets through the dynamics of a capacitor[J]. Expert Systems with Applications, 2021, 163: No.113785.
[10] TSAGKIAS M, WEERKAMP W, DE RIJKE M. Predicting the volume of comments on online news stories[C]// Proceedings of the 18th ACM Conference on Information and Knowledge Management. New York: ACM, 2009:1765-1768.
[11] FIGUEIREDO F, BENEVENUTO F, ALMEIDA J. The tube over time: characterizing popularity growth of YouTube videos[C]// Proceedings of the 4th ACM International Conference on Web Search and Web Data Mining. New York: ACM, 2011:745-754.
[12] 钟志豪,肖井华,吴晔,等. 基于抖音平台的在线短视频流行度建模研究[J]. 电子科技大学学报, 2021, 50(5):774-781.(ZHONG Z H, XIAO J H, WU Y, et al. Modeling dynamics of online short video popularity based on Douyin platform[J]. Journal of University of Electronic Science and Technology of China, 2021, 50(5):774-781.)
[13] GAO X F, ZHENG Z W, CHU Q Q, et al. Popularity prediction for single tweet based on heterogeneous Bass model[J]. IEEE Transactions on Knowledge and Data Engineering, 2021, 33(5):2165-2178.
[14] HU Y, HU C J, FU S S, et al. Predicting the popularity of viral topics based on time series forecasting[J]. Neurocomputing, 2016, 210:55-65.
[15] LI J N, GAO Y R, GAO X F, et al. SENTI2POP: sentiment‑ aware topic popularity prediction on social media[C]// Proceedings of the 2019 IEEE International Conference on Data Mining. Piscataway: IEEE, 2019: 1174-1179.
[16] WANG X, WANG C, DING Z Y, et al. Predicting the popularity of topics based on user sentiment in microblogging websites[J]. Journal of Intelligent Information Systems, 2018, 51(1): 97-114.
[17] GUPTA M, GAO J, ZHAI C X, et al. Predicting future popularity trend of events in microblogging platforms[J]. Proceedings of the American Society for Information Science and Technology, 2012, 49(1):1-10.
[18] 王新乐,杨文峰,廖华明,等. 基于多维度特征的主题标签流行度预测[J]. 山东大学学报(理学版), 2020, 55(1):94-101.(WANG X L, YANG W F, LIAO H M, et al. Popularity prediction of hashtags based on multi‑dimensional features[J]. Journal of Shandong University (Natural Science), 2020, 55(1):94-101.)
[19] MATSUBARA Y, SAKURAI Y, PRAKASH B A, et al. Rise and fall patterns of information diffusion: model and implications[C]// Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2012: 6-14.
Popularity prediction method of Twitter topics based on evolution patterns
XIE Weifan1,2, GUO Yan1*, KUANG Guangsheng1,3, YU Zhihua1, XUE Yuanhai1, SHEN Huawei1
(1,,,100190,;2,,101408,;3,,101408,)
A popularity prediction method of Twitter topics based on evolution patterns was proposed to address the problem that the differences between evolution patterns and the time‑effectiveness of prediction were not taken into account in previous popularity prediction methods. Firstly, the‑SC (‑Spectral Centroid) algorithm was used to cluster the popularity sequences of a large number of historical topics, and 6 evolution patterns were obtained. Then, a Fully Connected Network (FCN) was trained as the prediction model by using historical topic data of each evolution pattern. Finally, in order to select the prediction model for the topic to be predicted, Amplitude‑Alignment Dynamic Time Warping (AADTW) algorithm was proposed to calculate the similarity between the known popularity sequence of the topic to be predicted and each evolution pattern, and the prediction model of the evolution pattern with the highest similarity was selected to predict the popularity. In the task of predicting the popularity of the next 5 hours based on the known popularity of the first 20 hours, the Mean Absolute Percentage Error (MAPE) of the prediction results of the proposed method was reduced by 58.2% and 31.0% respectively, compared with those of the Auto‑Regressive Integrated Moving Average (ARIMA) method and method using a single fully connected network. Experimental results show that the model group based on the evolution patterns can predict the popularity of Twitter topic more accurately than single model.
Twitter topic; evolution pattern; popularity prediction; social network; time series
This work is partially supported by National Natural Science Foundation of China (U21B2046).
XIE Weifan, born in 1997, M. S. candidate. His research interests include popularity prediction.
GUO Yan, born in 1974, Ph. D., senior engineer. Her research interests include network information acquisition, network content processing.
KUANG Guangsheng, born in 1995, M. S. candidate. His research interests include natural language processing, data fusion.
YU Zhihua, born in 1973, Ph. D., chief senior engineer. His research interests include internet public opinion analysis.
XUE Yuanhai, born in 1987, Ph. D., senior engineer. His research interests include information retrieval, big data.
SHEN Huawei, born in 1982, Ph. D., research fellow. His research interests include social computing, data mining, machine learning.
TP181
A
1001-9081(2022)11-3364-07
10.11772/j.issn.1001-9081.2022010045
2022⁃01⁃17;
2022⁃03⁃03;
2022⁃03⁃07。
国家自然科学基金资助项目(U21B2046)。
解伟凡(1997—),男,山西运城人,硕士研究生,主要研究方向:流行度预测;郭岩(1974—),女,陕西西安人,高级工程师,博士,主要研究方向:网络信息获取、网络内容处理;匡广生(1995—),男,江西赣州人,硕士研究生,主要研究方向:自然语言处理、数据融合;余智华(1973—),男,江西吉安人,正高级工程师,博士,主要研究方向:网络舆情分析;薛源海(1987—),男,云南玉溪人,高级工程师,博士,主要研究方向:信息检索、大数据;沈华伟(1982—),男,河南周口人,研究员,博士,主要研究方向:社会计算、数据挖掘、机器学习。

