基于混合特征建模的图卷积网络方法

李卓然，冶忠林，赵海兴*，林晶晶

基于混合特征建模的图卷积网络方法

李卓然1，2，3，4，冶忠林1，2，3，4，赵海兴1，2，3，4*，林晶晶1，2，3，4

（1.青海师范大学 计算机学院，西宁 810016； 2.省部共建藏语智能信息处理及应用国家重点实验室（青海师范大学），西宁 810008； 3.藏文信息处理教育部重点实验室（青海师范大学），西宁 810008； 4.青海省藏文信息处理与机器翻译重点实验室（青海师范大学），西宁 810008）（ ∗ 通信作者电子邮箱h.x.zhao@163.com）

对于网络中拥有的复杂信息，需要更多的方式抽取其中的有用信息，但现有的单特征图神经网络（GNN）无法完整地刻画网络中的相关特性。针对该问题，提出基于混合特征的图卷积网络（HDGCN）方法。首先，通过图卷积网络（GCN）得到节点的结构特征向量和语义特征向量；然后，通过改进基于注意力机制或门控机制的聚合函数选择性地聚合语义网络节点的特征，增强节点的特征表达能力；最后，通过一种基于双通道图卷积网络的融合机制得到节点的混合特征向量，将节点的结构特征和语义特征联合建模，使特征之间互相补充，提升该方法在后续各种机器学习任务上的表现。在CiteSeer、DBLP和SDBLP三个数据集上进行实验的结果表明，与基于结构特征训练的GCN相比，HDGCN在训练集比例为20%、40%、60%、80%时的Micro‑F1值平均分别提升了2.43、2.14、1.86和2.13个百分点，Macro‑F1值平均分别提升了1.38、0.33、1.06和0.86个百分点。用拼接或平均值作为融合策略时，准确率相差不超过0.5个百分点，可见拼接和平均值均可作为融合策略。HDGCN在节点分类和聚类任务上的准确率高于单纯使用结构或语义网络训练的模型，并且在输出维度为64、学习率为0.001、2层图卷积层和128维注意力向量时的效果最好。

注意力机制；门控机制；双通道图卷积网络；结构特征；语义特征

0 引言

近年来，卷积神经网络（Convolutional Neural Network， CNN）因具有强大的特征表征能力和不依赖于大量先验知识的特点而快速发展，并借由其强大的建模能力成为研究热点。CNN在图像处理［1-2］、自然语言处理（Natural Language Processing， NLP）［3-4］以及旋转机械［5-6］等领域明显提升了各种机器学习任务的性能，然而CNN只能处理具有平移不变性特点的欧氏空间数据，如图像、语音等，但生活中的许多关系更需要用一种非欧氏空间数据——图数据——自然地表示，例如社交网络［7-8］、生物信息网络［9-10］和交通网络［11-12］等。不同于图像等欧氏空间数据，图数据局部结构各异，不满足平移不变性，考虑到CNN在图像识别领域的成功，如何在图数据上定义CNN成为研究热点。

Bruna等［13］基于卷积定理于2014年提出了Spectral CNN，模仿CNN特性，通过叠加多层图卷积，并且为每一层都定义了卷积核和激活函数，构成了图卷积网络（Graph Convolutional Network， GCN）。由于GCN时空复杂度较高，随后Defferrard等［14］于2016年提出了ChebNet，通过将切比雪夫多项式作为卷积核来降低时空复杂度。由于拉普拉斯矩阵的特征值分解复杂度很高，Hammond等［15］为了避免拉普拉斯矩阵的特征值分解，利用切比雪夫多项式的阶截断代替卷积核，将卷积核的建模范围从整个图转换到节点的阶邻居，并减少了卷积核的参数数量。Kipf等［16］使用一阶近似ChebNet提出了一种层级传播方式，每个图卷积层仅聚合一阶邻居，并且多个图卷积层可以共享一个卷积核，显著减少了参数数量；而且随着层数的增加，可以聚合远距离邻节点的信息量越多，不需要进行拉普拉斯矩阵的特征值分解，降低了时间复杂度。这些方法都是在谱域的角度定义图卷积，而基于空域的方法则出现得更早，并且在后期更受欢迎。早期的图神经网络（Graph Neural Network， GNN）要求节点聚合其邻节点信息达到一个收敛状态，可能导致节点无法被区分而出现过平滑现象。

在NLP中，节点的文本可以提供丰富的特征信息，不仅可以有效弥补因为结构特征稀疏而导致的训练不充分问题，还可以丰富节点的特征信息，从而提升分类任务的准确性。现有的图表示学习算法有一些是基于结构与文本联合建模的：TADW（Text‑Associated DeepWalk）［17］分别学习网络的结构表示和文本表示，然后将二者通过拼接的方式融入模型；NRNR（Network Representation learning algorithm using the optimizations of Neighboring vertices and Relation model）［18］提出了邻节点优化的网络表示学习（Network Representation Learning，NRL），基于知识表示学习中的关系模型对混合特征网络进行联合建模；TDNR（Tri‑party Deep Network Representation learning using inductive matrix completion）［19］将网络结构、文本特征和边的连接确定度等特征融合到RNL框架中，使学习到的表示向量包含了更多的网络属性信息；HSNR（Network Representation learning algorithm using Hierarchical Structure embedding）［20］从知识表示的角度引入了多关系建模思想，并将节点之间的关系转化为知识三元组形式，提出了一种联合学习模型将节点三元组关系嵌入到网络表示向量中。

在NRL任务中，通过浅层神经网络将文本特征和结构特征联合建模的研究较多，这些研究表明：混合特征建模在下游机器学习任务中的性能更优。但在GNN研究中，结构和文本联合建模的工作非常少，网络除了结构特征，节点的文本特征也是一个非常重要的参考特征，研究通过GNN如何将结构和文本特征联合建模是一项非常具有挑战性的工作。因此，本文提出一种基于混合特征的图卷积网络HDGCN（Hybrid Dual Graph Convolutional Network based on hybrid feature）。首先，将节点的标题作为语义特征并构造语义网络，将节点间的引用关系作为结构特征构造结构网络；其次，引入GCN学习网络中节点的结构特征向量和语义特征向量；然后，使用改进的聚合函数对语义特征进行聚合；最后，基于双通道图卷积网络拼接结构特征向量和语义特征向量。

综上所述，本文主要工作如下：

1）HDGCN引入注意力机制提升性能，因为注意力机制的学习参数仅与节点特征相关，与图结构关系不大。GCN学习的参数和图结构密切相关，每次计算都要更新图的全部节点，所以在归纳任务中表现一般。根据注意力机制设计聚合函数，计算节点间的权重系数，可以扩展到大规模数据集，增强泛化能力。对于不同度的节点，可以赋予相对应的权重体现最具有影响力的输入。

2）语义网络中节点存在部分弱相关邻节点，可能导致噪声数据影响HDGCN的训练效果，本文采用门控机制设计聚合函数控制节点特征信息流向，增强节点的特征表达能力，降低噪声的干扰。

3）基于语义特征或基于结构特征反映的节点信息不完整，将两种单特征融合为混合特征，充分利用了两种特征之间的互补性和多样性，增强节点表达能力。在三个基准测试数据集上验证本文模型，实验结果表明GCN中混合特征比单特征的准确率有明显提升。

1 相关工作

NRL先将网络中的节点映射为低维、稠密、实值向量表示，再用于各种机器学习任务。DeepWalk［21］是NRL最著名的工作，它采用随机游走方法得到节点序列，并将一个序列看作一个句子，序列中的节点元素看作单词，通过Word2Vec算法将每个顶点表示为一个低维向量。DeepWalk在图数据上利用自然语言处理方法学习节点表示，但网络中节点间结构关系比词上下文关系更复杂，并且通常网络中的边包含权重，Word2Vec算法目前不能解决该问题。LINE（Large‑scale Information Network Embedding）［22］定义一阶相似度和二阶相似度代替随机游走算法。受深度学习启发，SDNE（Structural Deep Network Embedding）［23］引入深度自编码器获得节点的一阶和二阶相似度。由于DeepWalk不能完整地保留网络结构信息，Node2Vec［24］优化了随机游走算法，提出了广度优先策略和深度优先策略。随着深度学习的兴起，神经网络应用于图数据利用end‑to‑end方式学习节点表示产生了一个新的研究热点——图神经网络（GNN）。

GNN分为基于谱域和空域两种方法。由于图数据不具有平移不变性的特点，CNN不能直接应用在图上，谱图理论的工作为定义图卷积提供了方法：先使用傅里叶变换，使节点嵌入从空域转换到谱域；再利用傅里叶逆变换将节点嵌入转换到原空间实现图卷积操作；反复执行图卷积操作，使节点对邻居节点的依赖性降低，能很好地完成图数据中更加复杂的学习任务。文献［16］中提出了经典的GCN，随着后续工作对GCN的不断改进和完善，该模型的基本结构由输入层、隐藏层和输出层三部分组成。其中隐藏层由图卷积层和池化层构成：图卷积层用来抽取图上每个节点邻接节点的特征，池化层通常用来降低特征维度。首先，图数据经过隐藏层提取每个节点的邻接节点特征，如果模型中参数太多，而训练样本太少，则通过Dropout在每个训练批次中随机丢弃一半的隐藏层节点；然后，再对输出的特征矩阵进行卷积操作；最后，用softmax激活函数将输出的节点嵌入映射到（0，1）区间，可以看作当前属于各个分类的概率。将模型输出结果作为预测值和真实值进行比较获得误差，通过反向传播将误差从后向前依次传递，并求出每一层的误差作为修改该层参数的依据。循环执行此操作直至收敛或预设的训练步为止。上述模型都使用原始图结构来表示节点间的关系，但是，不同节点间可能存在潜在的关系。2018年，Li等［25］提出了一种自适应图卷积网络（Adaptive Graph Convolutional neural Network， AGCN）来学习节点之间潜在的关系。同年，Zhuang等［26］针对图的全局和局部一致性提出了对偶图卷积网络（Dual Graph Convolutional Network， DGCN），使用两个不同的卷积获得局部一致性和全局一致性，并采用无监督损失对它们同时进行参数更新。2019年，Xu等［27］采用图小波变换代替图傅立叶变换，提出了图小波神经网络（Graph Wavelet Neural Network， GWNN）。GWNN有两个优点：无需矩阵分解即可快速得到图的小波变换；图小波具有稀疏性和局部性，分类的准确率结果更好，更易于解释。

基于空域的方法的核心思想是通过定义聚合函数对卷积核建模，迭代式地聚合邻居节点的特征，进而更新当前节点的特征。2009年，Scarselli等［28］提出了GNN，将循环递归函数作为聚合函数，每个节点通过聚合邻节点信息更新自身表达。2017年，Li等［29］提出了GG‑NN（Gated Graph Neural Network），利用门控循环网络更新节点自身表达，不再要求图收敛。2016年，DCNN（Diffusion Convolutional Neural Network）［30］将图卷积看作扩散过程，节点间的信息以一定的概率传播，相邻节点间信息传播概率更高。2017年，Hamilton等［31］提出了GraphSAGE（Graph SAmple and aggreGatE），给出了均值聚合、长短期记忆（Long Short‑Term Memory， LSTM）聚合和池化聚合三种聚合函数更新节点状态。Gilmer等［32］发现所有基于空域的都是节点将邻节点信息以某种形式聚合来更新节点状态，旨在将不同的模型集成到一个框架中，因此提出了一个基于空域图卷积的通用框架MPNN（Modified Probabilistic Neural Network）用于化学分子性质的预测。2017年，Monti等［33］尝试整合基于非欧空间模型，提出了MoNet框架。2018年，Wang等［34］通过整合若干种自注意力方法，提出了非局部神经网络（Non Local Neural Network， NLNN），非局部操作将某个位置的隐藏状态计算为所有可能状态的特征加权和。Battaglia等［35］提出了图网络（Graph Network， GN），它为节点级学习、边级学习和图级学习定义了一个更通用的框架。由于邻节点的影响不同，需要对它们进行区别对待，2018年，Veličković等［36］引入注意力机制定义聚合函数，通过对周围节点的表达加权求和更新节点自身表达。同年，Zhang等［37］提出了门控注意网络（Gated Attention Network， GaAN），它使用一种自注意力机制从不同的注意力头中收集信息，取代GAT（Graph ATtention）的平均操作。基于空域的方法使节点聚合了大量的周围节点信息，为了获得更重要的信息，增强节点特征的表达能力，使下游机器学习任务有更好的效果，引入注意力机制和门控循环单元（Gated Recurrent Unit， GRU）［38］到GNN中。GRU包含重置门和更新门，其中，重置门将新信息与之前的记忆结合，更新门定义了之前记忆与时间步相对应的量。更新门以门控形式控制信息流入，决定了传递到下游任务的上游信息的数量，或者两个时间步之间的信息传递数量，缓解了梯度弥散的风险。反之，重置门是一个由0和1作为门控值组成的向量，门控值决定了门控的大小，Hadamard乘积决定了上游信息被遗忘的数量，使用更新门收集当前和之前最终记忆信息，同时相加得到GRU最终的输出内容。Tree LSTM、Graph LSTM［39］、Sentence LSTM［40］在传播过程中使用GRU或LSTM［41］等门机制，以减少GNN的计算限制，并减少节点信息在图结构中的传播时间。2020年，Li等［42］除了定义注意力机制为聚合函数，还引入门单元到聚合函数。

2 基于混合特征的双通道图卷积网络

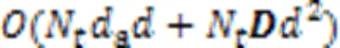
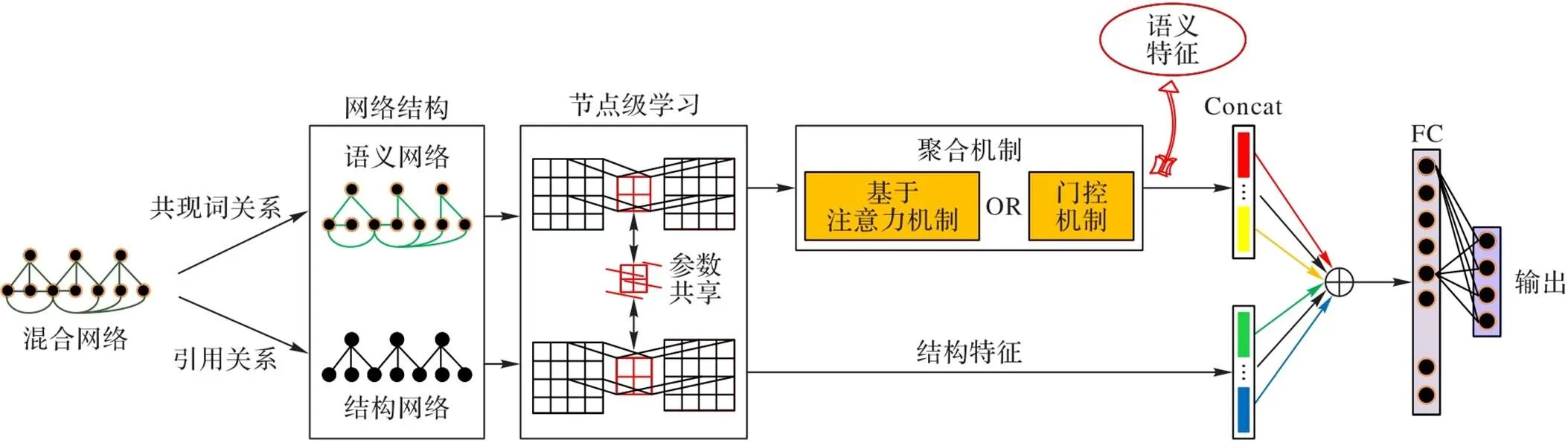
图1　HDGCN框架

2.1　符号和定义

2.2　节点级学习

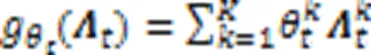
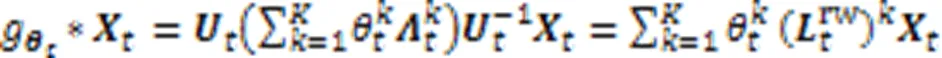
2.3　特征聚合

1）基于注意力机制的聚合函数。

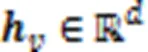
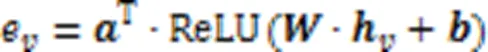
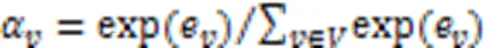
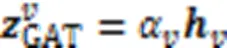
2）基于GRU的聚合函数。

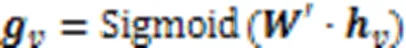
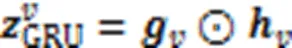
2.4特征融合

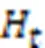
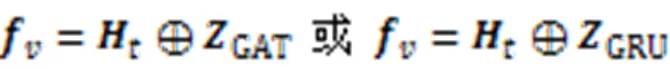
2.5　训练方法

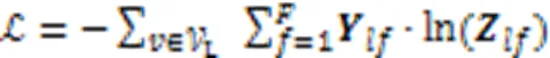
3 实验与结果分析

影响分类任务的主要因素是网络建模能力和基于注意力或门控聚合函数。其中，影响网络建模效果的因素主要是训练模型的数据集，权重矩阵的初始化，基本单元中卷积层的维度、学习率，模型中基本单元的个数、激活函数等。

3.1　数据集的选择

为评估HDGCN的有效性，使用三个引文网络数据集，包括学术网络数据集CiteSeer、DBLP（DataBase systems and Logic Programming）和SDBLP（Simplified DataBase systems and Logic Programming），它们的统计数据如表1所示。每个数据集根据关系类型划分为语义网络和结构网络，节点代表文献。在语义网络中，节点间连边关系根据词共现关系构造，即在每个节点的标题中，如果出现相同的词，则节点间存在连边关系；在结构网络中，节点间连边关系依据不同文献之间的引用关系确定。SDBLP是DBLP中删除引用数小于3的节点，即节点度小于3的节点被删除。

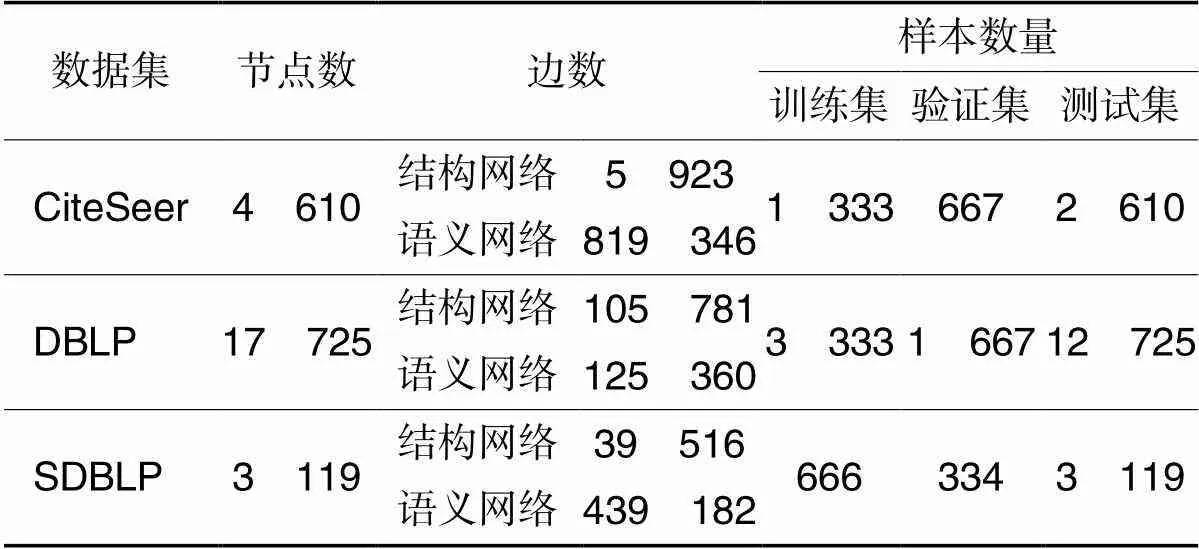
表1　数据集统计信息

3.2　节点分类

3.2.1对比实验

1）DeepWalk：一种将随机游走和Word2Vec相结合的图结构数据挖掘算法，它能够学习网络的隐藏信息，将图中的节点表示为一个包含潜在信息的向量。

2）LINE：对节点一阶相似度和二阶相似度进行建模，根据权重对边进行采样训练，可用于大规模有向图、无向图以及边有权重的网络进行节点表示。

3）Text Feature（TF）：将网络节点的文本内容转化为共现矩阵，然后使用奇异值分解（Singular Value Decomposition， SVD）去分解该共现矩阵，从而得到一个语义特征向量。

4）DeepWalk+TF：将DeepWalk和TF生成的网络表示向量按列拼接。

5）GraRep：用低维向量表示图中节点的向量，并将图的全局结构信息整合到学习过程。

如表2所示：在CiteSeer中，节点的语义特征在分类任务的准确率优于DeepWalk和LINE；将TF的特征向量与DeepWalk表示向量进行拼接，其准确率优于DeepWalk或文本特征TF；本文提出的HDGCN通过双通道图卷积网络和聚合函数将语义特征融入到网络的向量表示中，准确率优于DeepWalk+TF，也优于其他对比算法。

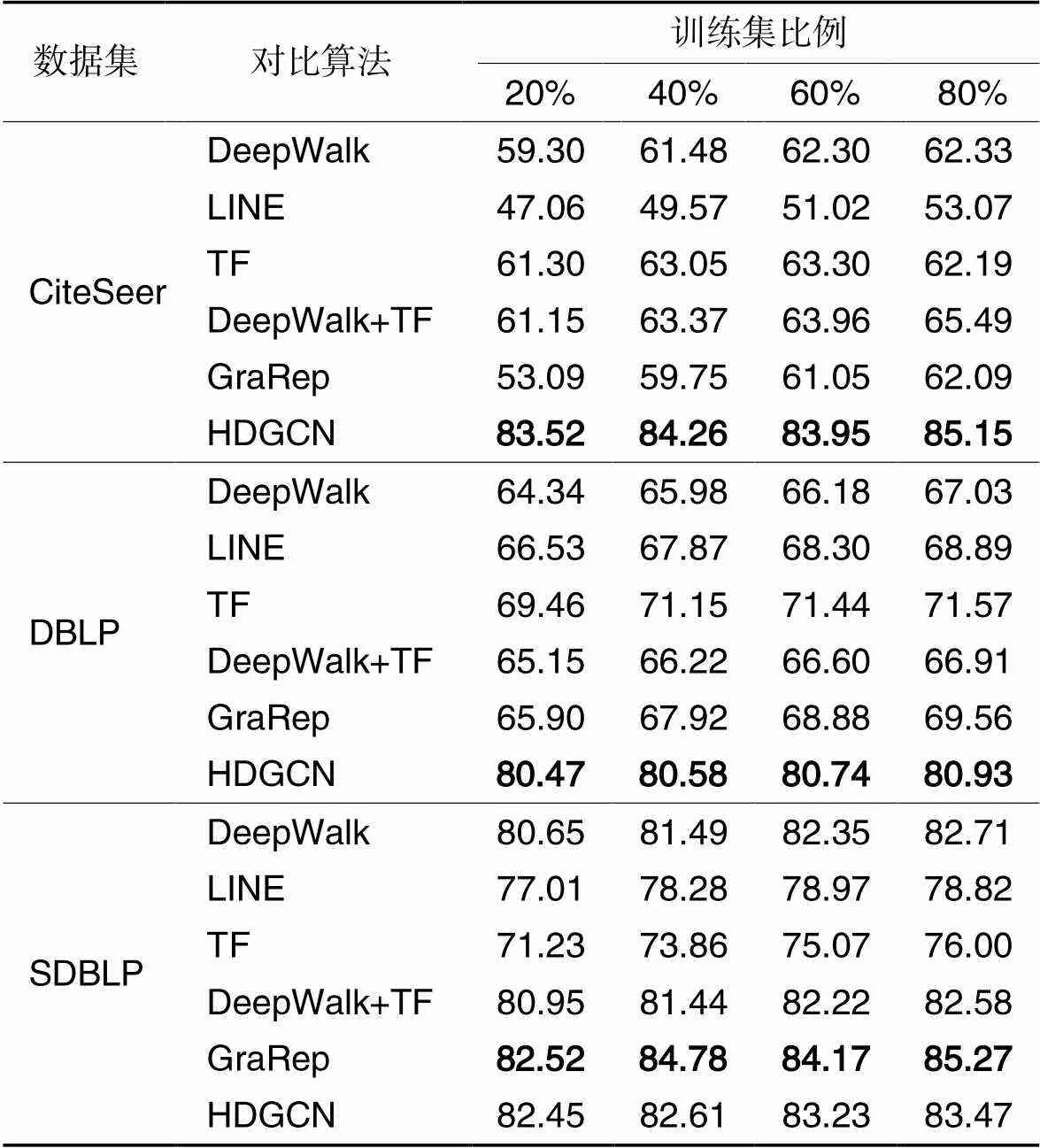
表2　不同训练集比例下的节点分类任务准确率 单位： %

在DBLP中，虽然语义特征随着训练集比例的增加，其准确率也越来越优于DeepWalk，但是，将DeepWalk与TF结合得到的结果却低于DeepWalk或TF。本文提出的HDGCN分类准确率远优于DeepWalk、LINE、GraRep等算法。

在SDBLP中，基于矩阵分解的高阶网络表示学习GraRep在分类任务中取得了很好的结果。由于SDBLP是稠密图，语义特征的节点分类准确率最差，所以，将DeepWalk和TF拼接后的分类准确率与DeepWalk相比没有优势。通过实验得到HDGCN分类性能劣于GraRep，原因是稠密图中，语义特征包含了许多噪声数据，将其融入网络的表示向量中会影响分类准确率。

3.2.2消融实验

如图2所示，在SDBLP数据集上，基于混合特征训练的HDGCN的节点分类准确率呈现了先下降后上升的趋势；但是在CiteSeer和DBLP数据集上，准确率曲线呈现显著的上升趋势。主要原因是在稠密图上：HDGCN借助密集的边连接可以充分地反映图的结构特征，但是，语义特征使许多弱关联邻节点与中心节点的关系增强甚至成为邻居节点，作为噪声数据影响HDGCN反映图语义特征的有效性，因此，特征融合后的混合特征呈现出下降趋势。由于DBLP数据集是大规模的稀疏图，HDGCN受限于其规模不能充分地反映图的不同特征，准确率的跨度低于SDBLP和CiteSeer数据集。

表3　不同训练集比例下节点分类任务的Micro‑F1和Macro‑F1对比 单位： %

图2　不同训练集比例下的节点分类准确率变化曲线

3.3　参数影响与选择

3.3.1卷积核初始化的选择

由于一般神经网络在前向传播时神经元输出值的方差会不断增大，为了使网络中的信息更好地流动，每层输出方差应该尽量相等，使用Xavier理论上可以保证每层神经元输入输出方差一致，避免了所有输出值都趋向于0。标准正态分布可以将输入值强行变为标准正态分布，使激活函数值在非线性函数中比较敏感的区域：梯度增大，收敛速度加快。截断正态分布指定平均值和标准差，但是大于平均值2个标准差的值被删除且重新选择。图3是卷积核初始化方法对模型训练的影响。如图3所示，使用Xavier初始化卷积核可以使HDGCN在最少的迭代次数情况下趋于稳定，虽然在DBLP数据集上使用正态分布方法相较于Xavier方法更快地使HDGCN达到稳定状态，但其准确率均高于使用正态分布和截断正态分布初始化卷积核情况下取得的准确率。

3.3.2输出维度的影响

3.3.3学习率的选择

学习率是通过损失函数的梯度调整指导权重矩阵的超参数。学习率越低，损失函数变化速度越慢。虽然低学习率不影响极小值的选择，但会延长收敛的时间；学习率太高，梯度下降的幅度可能会超过最优值。另外，学习速率对模型达到最优准确率的速度也有影响。图5为学习率对训练的影响，可以看出，CiteSeer和SDBLP数据集上混合网络对应的学习率为0.001，并且当学习率大于0.001时，混合网络的分类效果均优于结构网络和语义网络。为了避免因梯度下降的幅度过大而错过最优值，学习率选择0.001。

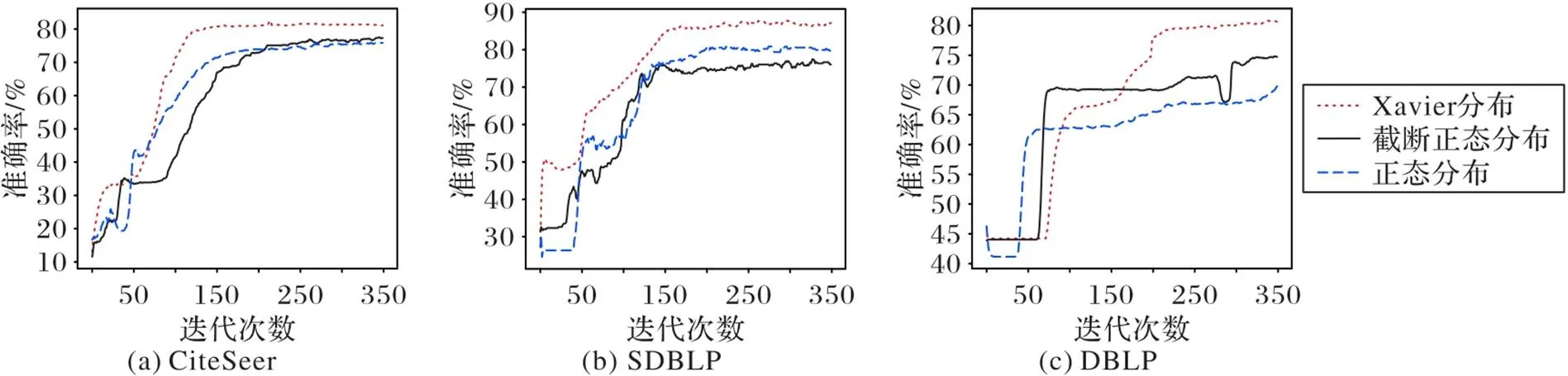
图3　卷积核初始化方法对节点分类准确率的影响

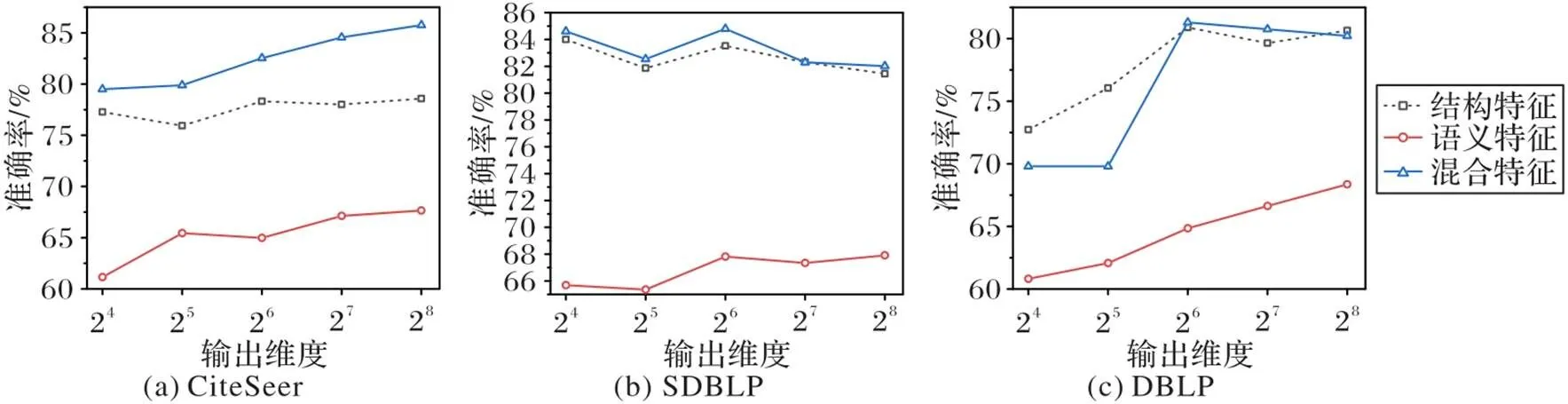
图4　输出维度对节点分类准确率的影响

图5　学习率对节点分类准确率的影响

3.3.4模型层数的选择

众所周知，GCN是一个低通滤波器，这种特性可以使信号更加平滑；但这种优势若不加以控制则过犹不及，因为多次进行信号的平滑操作容易使节点信号趋于一致，丧失节点多样性的特征，使得以GCN为基础的下游任务难以进行，这种现象被称为过平滑（over‑smoothing）。

图6为卷积层数对训练的影响，可以看出：当卷积层数增加到8后，混合网络的准确率低于结构网络的准确率，且随着层数的增加，HDGCN的准确率逐渐降低，出现过平滑现象；在SDBLP中，卷积层数为8时HDGCN的学习效果最好；当CiteSeer中结构网络和语义网络的卷积层数大于2时，分类任务的准确率逐渐降低；受制于DBLP中混合网络存在大量的噪声数据，当卷积层数为4时，准确率到达峰值。因为在每个数据集上，混合网络的分类准确率在卷积层数为2、4、8时均高于结构网络，并且上述各个网络的准确率峰值对应的层数最多为8，为了避免过拟合，HDGCN选择2层卷积层。

3.3.5注意力向量维度的选择

3.4　节点聚类

本文通过使用K‑means类方法对节点进行聚类并且计算归一化互信息（Normalized Mutual Information， NMI）和调整兰德指数（Adjusted Rand Index， ARI）测试模型性能，K‑means聚类数和节点的类别数相同。节点聚类和分类任务使用相同的模型参数，表4的实验结果为10次实验的平均值。由于SDBLP数据集中基于结构特征的节点间联系紧密，聚类程度较高，但是，基于语义特征的节点间联系包含了大量的噪声，可能会影响节点的聚类效果；因此，基于混合特征的节点聚类效果相较于结构特征差距不明显。DBLP数据集数据量较大且具有较强的稀疏性，它基于结构特征的节点聚类效果明显弱于SDBLP和CiteSeer；因此，基于混合特征的节点聚类效果比结构特征差。

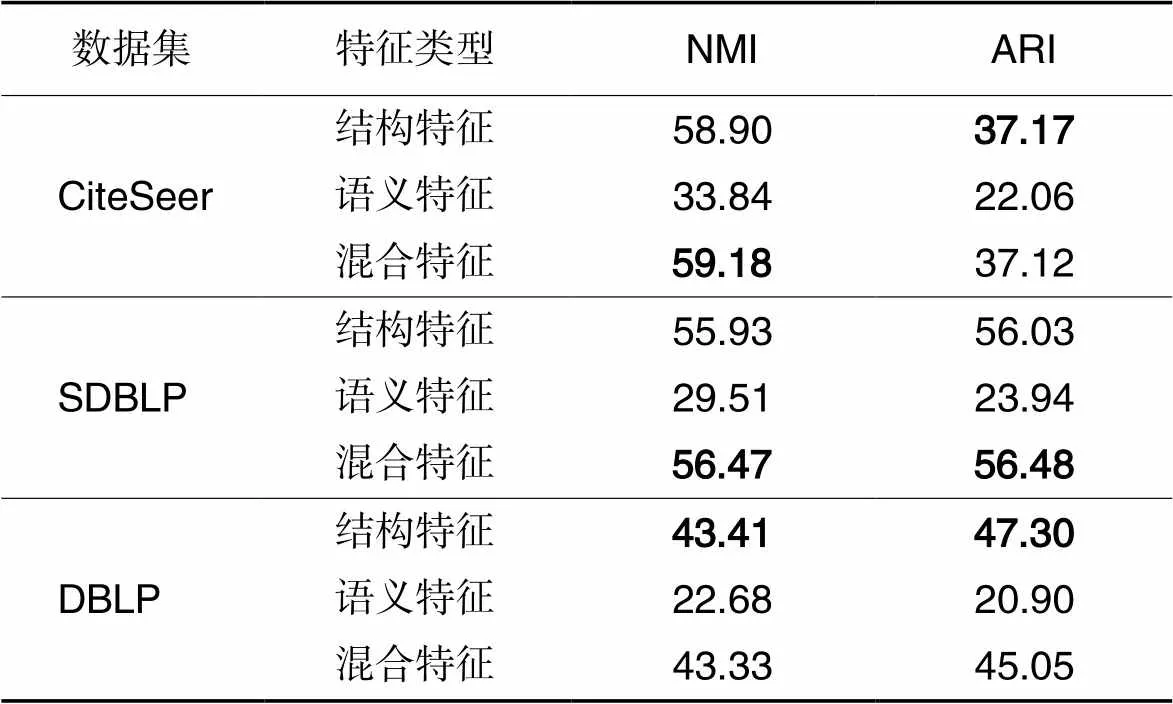
表4　三种特征在聚类任务下的NMI和ARI对比 单位： %

3.5　特征融合策略

本文将结构特征和文本特征融合为混合特征，融合策略如表5所示：在SDBLP和CiteSeer数据集上，mean作为融合策略时，模型效果最好：在DBLP数据集上，concat作为融合策略效果最好。但是，三种融合策略的结果差异性较小，不是影响模型性能的主要因素。

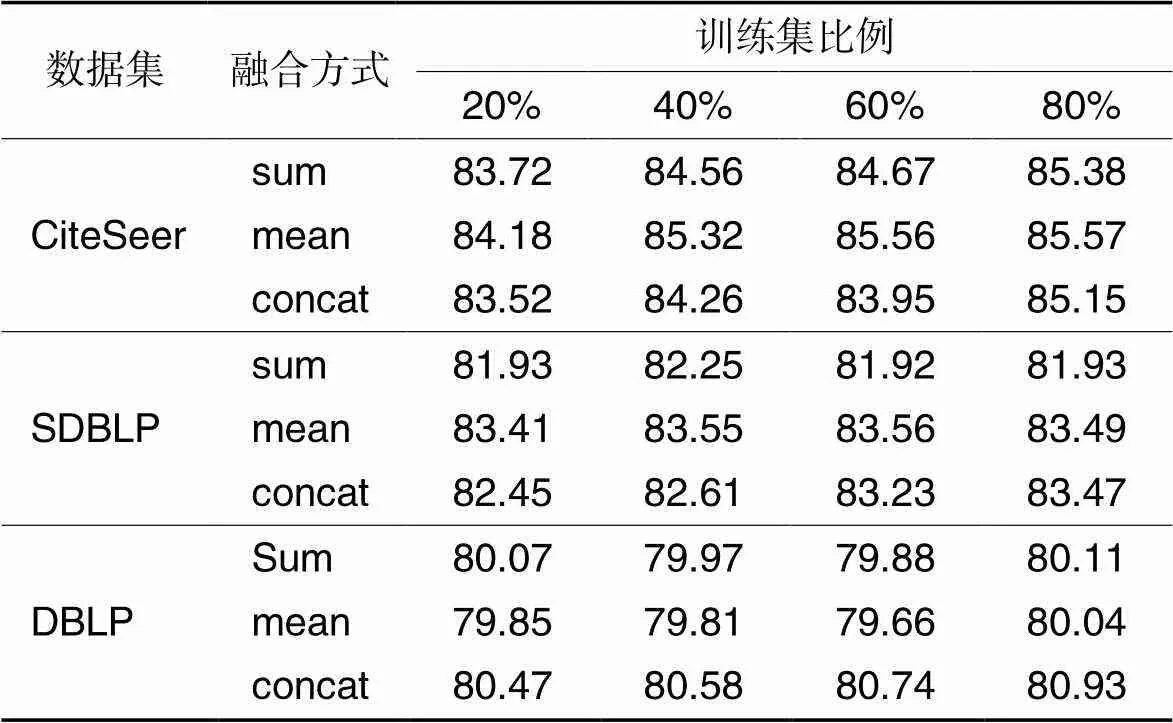
表5　不同训练集比例下三种融合方式的节点分类任务准确率 单位： %

3.6　节点分类任务可视化

为了能直观体现混合特征的优越性，本文通过t‑SNE将节点的嵌入表示映射到二维空间，在图8中，本文验证了基于混合特征、结构特征以及语义特征的节点嵌入表示，不同的颜色代表不同的研究类别。由图8可知，混合特征在下游任务中表现出众，更具体地说，基于混合特征的节点分类任务中，节点之间的相似性较高且相较于语义特征不同类别内的大部分节点具有明显的边界，并且对于基于结构特征的节点分类结果中未区分的节点，混合特征按节点所属类别对其进行分离；基于结构特征的分类任务中，部分节点没有明显的区分而紧密地聚集在一起；基于语义特征的分类任务中，由于存在大量的噪声数据，不同类别的节点之间不但没有明确的界限，还分散地交叉混合在一起。

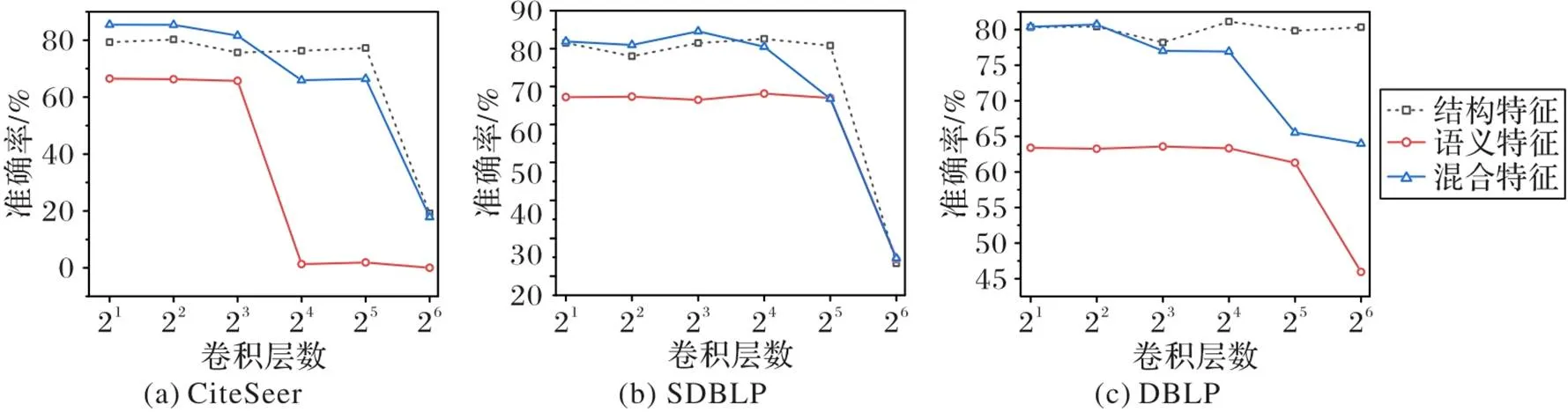
图6　卷积层数对节点分类准确率的影响

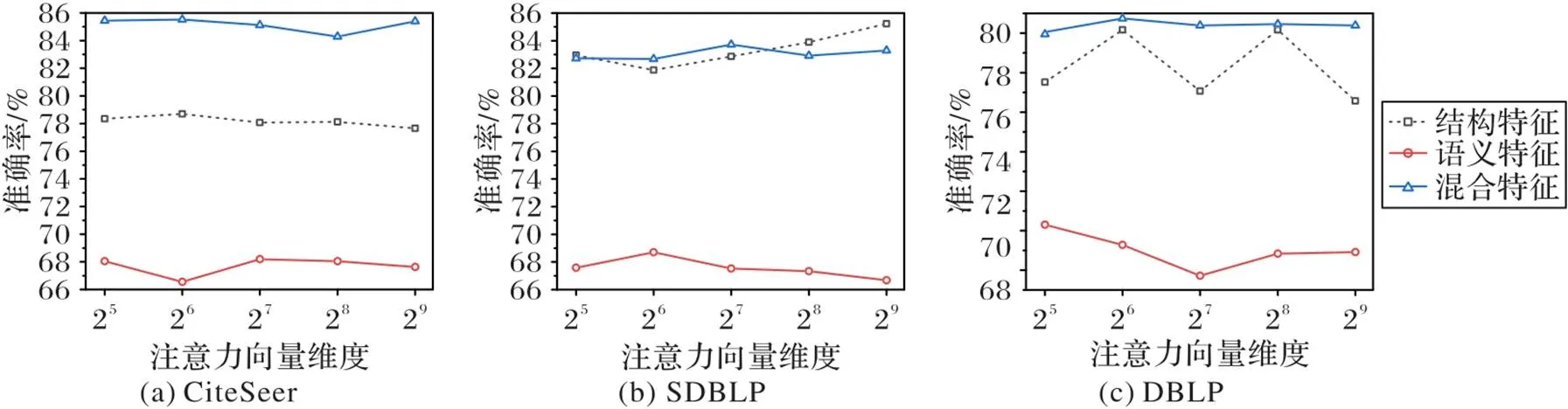
图7　注意力向量维度对节点分类准确率的影响

图8　CiteSeer数据集上特征嵌入的可视化

4 结语

本文通过构建双通道图卷积网络模型学习混合特征的节点嵌入表示。该模型首先将混合特征分解为两个单一类型特征：结构特征和语义特征；其次，将结构特征和语义特征作为图卷积层的输入抽取每个节点的特征；然后，为了提高模型泛化能力并抽取完整语义特征的节点表示，将基于注意力机制和门控机制的聚合函数作用于基于节点间语义关联的网络；最后，将聚合结果按行拼接、共享参数、协同训练得到下游任务的分类结果。实验结果表明，本文使用Xavier初始化卷积核；为了避免因梯度下降的幅度过大而错过最优值，学习率选择0.001；为了防止发生过平滑现象，设置2层图卷积；在不同数据集上，嵌入维度分别选择64和256，注意力向量维度分别选择128和64。在不同的机器学习任务中，基于HDGCN模型的混合特征节点嵌入的结果明显优于另外两种单一的特征类型。增加图卷积层的数量可以提高图卷积网络的性能，如何增加HDGCN的图卷积层数而且不发生过平滑现象也是一个潜在的研究问题。

[1] LIU Y， LIU S P， WANG Z F. A general framework for image fusion based on multi‑scale transform and sparse representation［J］. Information Fusion， 2015， 24： 147-164.

[2] EASLEY G， LABATE D， LIM W Q. Sparse directional image representations using the discrete shearlet transform［J］. Applied and Computational Harmonic Analysis， 2008， 25（1）：25-46.

[3] KALCHBRENNER N， GREFENSTETTE E， BLUNSOM P. A convolutional neural network for modelling sentences［C］// Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics （Volume 1： Long Papers）. Stroudsburg， PA： Association for Computational Linguistics， 2014： 655-665.

[4] LE Q， MIKOLOV T. Distributed representations of sentences and documents［C］// Proceedings of the 31st International Conference on Machine Learning. New York： JMLR.org， 2014：1188-1196.

[5] ZHAO M H， ZHONG S S， FU X Y， et al. Deep residual shrinkage networks for fault diagnosis［J］. IEEE Transactions on Industrial Informatics， 2020， 16（7）： 4681-4690.

[6] 李涛，段礼祥，张东宁，等. 自适应卷积神经网络在旋转机械故障诊断中的应用［J］. 振动与冲击， 2020， 39（16）：275-282， 288.（LI T， DUAN L X， ZHANG D N， et al. Application of adaptive convolutional neural network in rotating machinery fault diagnosis［J］. Journal of Vibration and Shock， 2020， 39（16）：275-282， 288.）

[7] KICK E L， McKINNEY L A， McDONALD S， et al. A multiple‑ network analysis of the world system of nations， 1995-1999［M］// SCOTT J， CARRINGTON P J. The SAGE Handbook of Social Network Analysis. Thousand Oaks， CA： SAGE Publications Ltd， 2014：311-328.

[8] LIAO L Z， HE X N， ZHANG H W， et al. Attributed social network embedding［J］. IEEE Transactions on Knowledge and Data Engineering， 2018， 30（12）：2257-2270.

[9] GLIGORIJEVIĆ V， BAROT M， BONNEAU R. deepNF： deep network fusion for protein function prediction［J］. Bioinformatics， 2018， 34（22）：3873-3881.

[10] SU C， TONG J， ZHU Y J， et al. Network embedding in biomedical data science［J］. Briefings in Bioinformatics， 2020， 21（1）：182-197.

[11] 杨力川. 基于深度学习的交通标志识别研究综述［J］. 现代计算机， 2021（15）：3-5， 11.（YANG L C. Summary of research on traffic sign recognition based on deep learning［J］. Modern Computer， 2021（15）：3-5， 11.）

[12] CUI Z Y， HENRICKSON K， KE R M， et al. Traffic graph convolutional recurrent neural network： a deep learning framework for network‑scale traffic learning and forecasting［J］. IEEE Transactions on Intelligent Transportation Systems， 2020， 21（11）： 4883-4894.

[13] BRUNA J， ZAREMBA W， SZLAM A， et al. Spectral networks and locally connected networks on graphs［EB/OL］. （2014-04-21）［2021-11-26］.https：//arxiv.org/pdf/1312.6203.pdf.

[14] DEFFERRARD M， BRESSON X， VANDERGHEYNST P. Convolutional neural networks on graphs with fast localized spectral filtering［C］// Proceedings of the 30th International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2016：3844-3852.

[15] HAMMOND D K， VANDERGHEYNST P， GRIBONVAL R. Wavelets on graphs via spectral graph theory［J］. Applied and Computational Harmonic Analysis， 2011， 30（2）：129-150.

[16] KIPF T N， WELLING M. Semi‑supervised classification with graph convolutional networks［EB/OL］. （2017-02-22）［2021-11-26］. https：//arxiv.org/pdf/1609.02907.pdf.

[17] YANG C， LIU Z Y， ZHAO D L， et al. Network representation learning with rich text information［C］// Proceedings of the 24th International Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2015：2111-2117.

[18] 冶忠林，赵海兴，张科，等. 基于多源信息融合的分布式词表示学习［J］. 中文信息学报， 2019， 33（10）：18-30.（YE Z L， ZHAO H X， ZHANG K， et al. Distributed word embedding via multi‑source information fusion［J］. Journal of Chinese Information Processing， 2019， 33（10）：18-30.）

[19] YE Z L， ZHAO H X， ZHANG K， et al. Tri‑party deep network representation learning using inductive matrix completion［J］. Journal of Central South University， 2019， 26（10）： 2746-2758.

[20] YE Z L， ZHAO H X， ZHU Y， et al. HSNR： a network representation learning algorithm using hierarchical structure embedding［J］. Chinese Journal of Electronics， 2020， 29（6）：1141-1152.

[21] PEROZZI B， AL‑RFOU R， SKIENA S. DeepWalk： online learning of social representations［C］// Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2014：701-710.

[22] TANG J， QU M， WANG M Z， et al. LINE： large‑scale information network embedding［C］// Proceedings of the 24th International Conference on World Wide Web. Republic and Canton of Geneva： International World Wide Web Conferences Steering Committee， 2015： 1067-1077.

[23] WANG D X， CUI P， ZHU W W. Structural deep network embedding［C］// Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2016： 1225-1234.

[24] GROVER A， LESKOVEC J. node2vec： scalable feature learning for networks［C］// Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2016： 855-864.

[25] LI R Y， WANG S， ZHU F Y， et al. Adaptive graph convolutional neural networks［C］// Proceedings of the 32nd AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2018：3546-3553.

[26] ZHUANG C Y， MA Q. Dual graph convolutional networks for graph‑based semi‑supervised classification［C］// Proceedings of the 2018 World Wide Web Conference. Republic and Canton of Geneva： International World Wide Web Conferences Steering Committee， 2018： 499-508.

[27] XU B B， SHEN H W， CAO Q， et al. Graph wavelet neural network［EB/OL］. （2019-04-12）［2021-11-26］.https：//arxiv.org/pdf/1904.07785.pdf.

[28] SCARSELLI F， GORI M， TSOI A C， et al. The graph neural network model［J］. IEEE Transactions on Neural Networks， 2009， 20（1）： 61-80.

[29] LI Y J， ZEMEL R， BROCKSCHMIDT M， et al. Gated graph sequence neural networks［EB/OL］. （2017-09-22）［2021-11-26］.https：//arxiv.org/pdf/1511.05493.pdf.

[30] ATWOOD J， TOWSLEY D. Diffusion‑convolutional neural networks［C］// Proceedings of the 30th International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2016：2001-2009.

[31] HAMILTON W L， YING R， LESKOVEC J. Inductive representation learning on large graphs［C］// Proceedings of the 31st International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2017：1025-1035.

[32] GILMER J， SCHOENHOLZ S S， RILEY P F， et al. Neural message passing for quantum chemistry［C］// Proceedings of the 34th International Conference on Machine Learning. New York： JMLR.org， 2017：1263-1272.

[33] MONTI F， BOSCAINI D， MASCI J， et al. Geometric deep learning on graphs and manifolds using mixture model CNNs［C］// Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway： IEEE， 2017：5425-5434.

[34] WANG X L， GIRSHICK R， GUPTA A， et al. Non‑local neural networks［C］// Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway： IEEE， 2018：7794-7803.

[35] BATTAGLIA P W， HAMRICK J B， BAPST V， et al. Relational inductive biases， deep learning， and graph networks［EB/OL］. （2018-10-17）［2021-11-26］.https：//arxiv.org/pdf/1806.01261.pdf.

[36] VELIČKOVIĆ P， CUCURULL G， CASANOVA A， et al. Graph attention networks［EB/OL］. （2018-02-04）［2021-11-26］.https：//arxiv.org/pdf/1710.10903.pdf.

[37] ZHANG J N， SHI X J， XIE J Y， et al. GaAN： gated attention networks for learning on large and spatiotemporal graphs［C］// Proceedings of the Thirty‑Fourth Conference on Uncertainty in Artificial Intelligence. Arlington， VA： AUAI Press， 2018： No.139.

[38] CHUNG J， GULCEHRE C， CHO K， et al. Empirical evaluation of gated recurrent neural networks on sequence modeling［EB/OL］. （2014-12-11）［2021-11-26］.https：//arxiv.org/pdf/1412.3555.pdf.

[39] LIANG X D， SHEN X H， FENG J S， et al. Semantic object parsing with Graph LSTM［C］// Proceedings of the 2016 European Conference on Computer Vision， LNCS 9905. Cham： Springer， 2016：125-143.

[40] ZHANG Y， LIU Q， SONG L F. Sentence‑state LSTM for text representation［C］// Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics （Volume 1： Long Papers）. Stroudsburg， PA： Association for Computational Linguistics， 2018：317-327.

[41] HOCHREITER S， SCHMIDHUBER J. Long short‑term memory［J］. Neural Computation， 1997， 9（8）：1735-1780.

[42] LI X H， WEN L J， QIAN C， et al. GAHNE： graph‑aggregated heterogeneous network embedding［C］// Proceedings of the IEEE 32nd International Conference on Tools with Artificial Intelligence. Piscataway： IEEE， 2020：1012-1019.

Graph convolutional network method based on hybrid feature modeling

LI Zhuoran1，2，3，4， YE Zhonglin1，2，3，4， ZHAO Haixing1，2，3，4*， LIN Jingjing1，2，3，4

（1，，810016，；2（），810008，；3，（），810008，；4（），810008，）

For the complex information contained in the network， more ways are needed to extract useful information from it， but the relevant characteristics in the network cannot be completely described by the existing single‑feature Graph Neural Network （GNN）. To resolve the above problems， a Hybrid feature‑based Dual Graph Convolutional Network （HDGCN） was proposed. Firstly， the structure feature vectors and semantic feature vectors of nodes were obtained by Graph Convolutional Network （GCN）. Secondly， the features of nodes were aggregated selectively so that the feature expression ability of nodes was enhanced by the aggregation function based on attention mechanism or gating mechanism. Finally， the hybrid feature vectors of nodes were gained by the fusion mechanism based on a feasible dual‑channel GCN， and the structure features and semantic features of nodes were modeled jointly to make the features be supplement for each other and promote the method􀆳s performance on subsequent machine learning tasks. Verification was performed on the datasets CiteSeer， DBLP （DataBase systems and Logic Programming） and SDBLP （Simplified DataBase systems and Logic Programming）. Experimental results show that compared with the graph convolutional network model based on structure feature training， the dual channel graph convolutional network model based on hybrid feature training has the average value of Micro‑F1 increased by 2.43， 2.14， 1.86 and 2.13 percentage points respectively， and the average value of Macro‑F1 increased by 1.38， 0.33， 1.06 and 0.86 percentage points respectively when the training set proportion is 20%， 40%， 60% and 80%. The difference in accuracy is no more than 0.5 percentage points when using concat or mean as the fusion strategy， which shows that both concat and mean can be used as the fusion strategy. HDGCN has higher accuracy on node classification and clustering tasks than models trained by structure or semantic network alone， and has the best results when the output dimension is 64， the learning rate is 0.001， the graph convolutional layer number is 2 and the attention vector dimension is 128.

attention mechanism; gating mechanism; dual channel graph convolutional network; structure feature; semantic feature

This work is partially supported by National Key Research and Development Program of China （2020YFC1523300）， Natural Science Foundation of Qinghai Province （2021‑ZJ‑946Q）， Middle‑Youth Natural Science Foundation of Qinghai Normal University （2020QZR007）.

LI Zhuoran， born in 1996， M. S. candidate. His research interests include data mining， graph neural network.

YE Zhongli， born in 1989， Ph. D.， associate professor. His research interests include question answering system， network representation learning.

ZHAO Haixing， born in 1969， Ph. D.， professor. His research interests include complex network， network reliability.

LIN Jingjing， born in 1986， Ph. D. candidate， lecturer. Her research interests include data mining， hypergraph neural network.

1001-9081（2022）11-3354-10

10.11772/j.issn.1001-9081.2021111981

2021⁃11⁃22；

2022⁃01⁃12；

2022⁃01⁃14。

国家重点研发计划项目（2020YFC1523300）；青海省自然科学基金资助项目（2021‑ZJ‑946Q）；青海师范大学自然科学中青年科研基金资助项目（2020QZR007）。

TP391

A

李卓然（1996—），男，内蒙古乌兰察布人，硕士研究生，CCF会员，主要研究方向：数据挖掘、图神经网络；冶忠林（1989—），男，青海民和人，副教授，博士，CCF会员，主要研究方向：问答系统、网络表示学习；赵海兴（1969—），男，青海湟中人，教授，博士，CCF会员，主要研究方向：复杂网络、网络可靠性；林晶晶（1986—），女，甘肃临洮人，讲师，博士研究生，CCF会员，主要研究方向：数据挖掘、超图神经网络。