基于主成分分析法的福建某滨海场地地下水水质评价

郭新强

(1.福建省197地质大队，福建 泉州 362011；2.长江大学继续教育学院，湖北 荆州 434023)

随着我国经济社会的快速发展，水环境污染问题日益突出，如何合理、客观地评价水质现状显得尤为重要，评价水质过程中因复杂多样的环境因素使得研究工作变得繁重，数据分析也相当困难，有时找不到水质恶化的原因[1]。目前国内外常用的水质评价方法有综合指数法[2]，污染指数法[3]，模糊综合评价法[4]，主成分分析法[5]，神经网络法[6]，物元评价法[7]等。

由于地区差异，水质污染的指标各不相同，真实的原始数据非常多，它们并不服从正态分布，通常是共线性或自相关的，由于这个原因，使用主成分分析、因子分析等多元方法[8]。主成分分析方法是一种降维的统计学方法，它将收集到的水质数据，在尽可能多地保留原始书记信息的情况下，用较少的几个综合因子来解释水质信息，进行水质综合评价。

本文以福建某滨海场地9个水质监测点采样数据作为研究对象，基于主成分分析法评价该场地地下水的水质，为保护和改善该场地地下水水环境质量提供指导。

1 研究方法

本研究使用SPSS软件对某滨海场地7项地下水质量指标进行主成分分析，其分析步骤如下：

(1)水质评价指标选取。选取溶解性总固体、硫酸盐、氯化物、高锰酸盐指数、硝酸盐、亚硝酸盐、氨氮等7个评价指标。

(2)对原始数据进行标准化处理。数据标准化的方法为Z-Score标准化法，消除不同水质指标之间量纲和数量级的影响。

(3)计算相关系数矩阵。

(4)计算主成分贡献率和累计贡献率，确定主成分个数。一般根据累计贡献率和特征值判断，累计贡献率达到80%以上，特征值大于1即可。

(5)计算主成分分值，确定综合函数，综合函数值越高，表明污染越严重，从而对各个监测点进行水质排序。

2 结果与分析

2.1 原始数据标准化

为消除原始数据不同水质指标之间量纲和数量级的影响。对数据进行标准化处理，处理结果见表1。

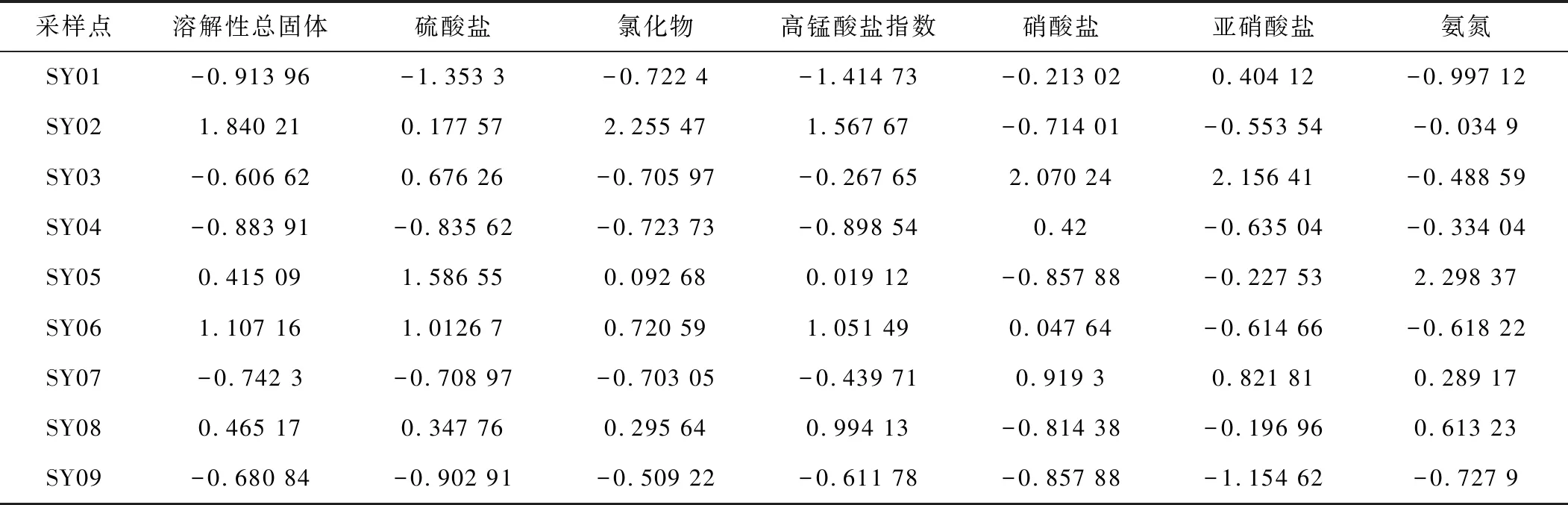
表1 标准化后数据

2.2 相关系数矩阵

运用KMO检验统计量和球形检验，判断标准化后的数据是否适合因子分析。使用统计软件SPSS计算得到KMO检验统计量为0.546，大于0.5；Bartlett球形度检验显著性概率P值为0.001，小于0.01。计算结果表明原始变量存在相关性，适宜做主成分分析(表2)。

表2 KMO和Bartlett检验结果

在标准化数据的基础上，计算相关系数矩阵，相关系数结果见表3。绝对值越大的相关系数，两个指标之间的相关性越强，相关系数呈正值，表明其呈正相关；相关系数呈负值，表明其呈负相关。溶解性总固体与氯化物相关系数(R)为0.965，是研究区内相关性最强的一组水质指标，说明溶解性总固体与氯化物来源相似性高；溶解性总固体与高锰酸盐指数(R=0.939)，氯化物与高锰酸盐指数(R=0.884)，硝酸盐与亚硝酸盐(R=0.822)具有较强的正相关关系；溶解性总固体与硫酸盐(R=0.622)，硫酸盐与高锰酸盐指数(R=0.633)、氨氮(R=0.622)具有中等的正相关关系；硫酸盐与氯化物(R=0.430)具有弱的正相关关系；溶解性总固体与硝酸盐(R=-0.441)、亚硝酸盐(R=-0.353)，氯化物与硝酸盐(R=-0.465)、亚硝酸盐(R=-0.389)，高锰酸盐指数与硝酸盐(R=-0.301)，硝酸盐与氨氮(R=-0.316)具有弱的负相关关系；其余水质指标之前的相关关系极弱或者无相关关系。

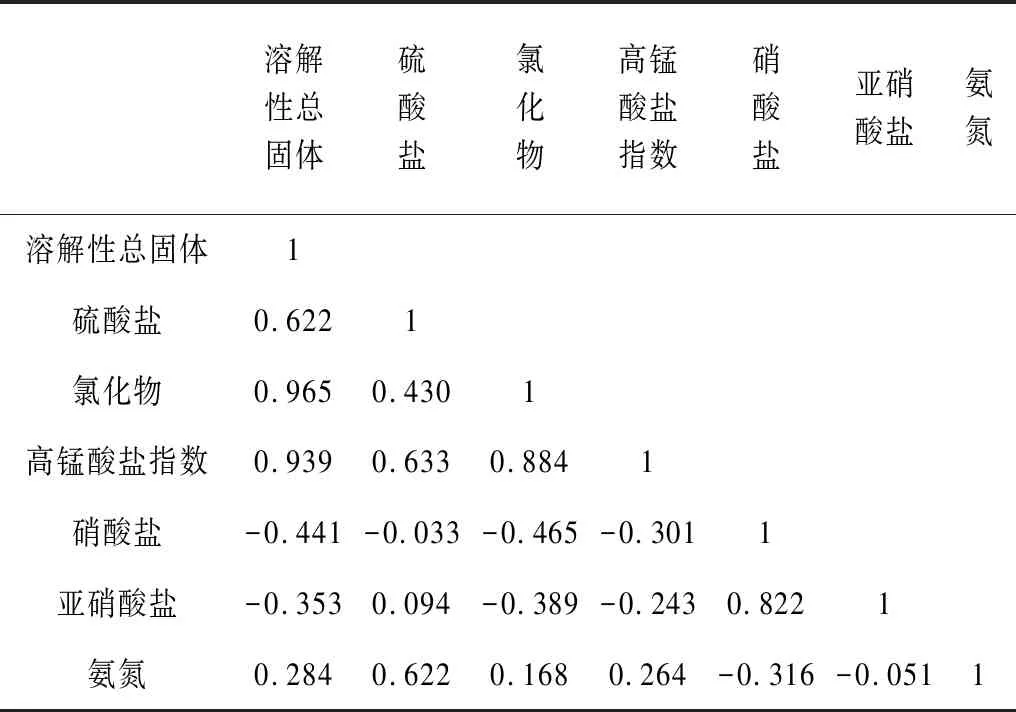
表3 相关系数矩阵

2.3 主成分确定

特征值λ在一定程度上影响主成分大小的指标，特征值λ>1的主成分具有较好的解释力度[5]。根据计算主成分特征值、方差及累积贡献率(表4)，结果显示特征值大于1的为前3个主成分，第一个主成分F1特征值λ1为3.806，第二个主成分F2特征值λ2为1.667，第三个主成分F3特征值λ3为1.082，对应的方差依次为：54.373%、23.812%、15.462%，第一主成分的方差值较大，超过50%，第二和第三主成分的方差值相对较小，说明本区地下水化学数据的收敛比较快，同时也表明影响该场地水质的污染源具有复杂多样性的特点。第一、第二和第三主成分累积方差贡献率为93.648%，凸显对变量的解释能力非常好，因此前3个主成分(F1、F2、F3)包含了原始数据7个水质指标的大多数信息，即提取3个主成分是合理的。

表4 特征值、方差及累积贡献率

根据主成分特征值曲线的碎石图(图1)，前3个主成分特征值曲线相对比较陡峭，所以提取前3个主成分对原始变量的信息有较好的解释力度；第四个主成分特征值λ4小于1，且该特征值后的曲线趋于平缓，说明其解释力度变弱。因此，确定主成分的数量为3个(F1、F2、F3)，可利用他们来评价地下水水质。

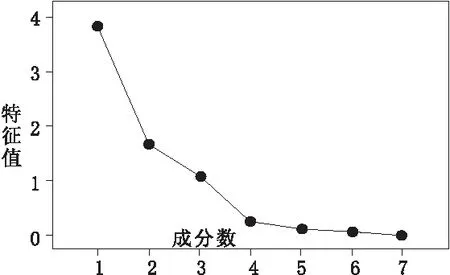
图1 主成分碎石图

2.4 初始因子载荷矩阵

初始因子载荷矩阵系数揭示水质指标和主成分之间的相关程度，用于比较不同主成分变量之间的变异程度。相关系数呈正值，表明其呈正相关；相关系数呈负值，表明其呈负相关；相关系数绝对值越接近1，相关程度越强，可作为地下水水质评价的主要控制指标[9-10]。主成分初始因子载荷矩阵结果显示(表5)。

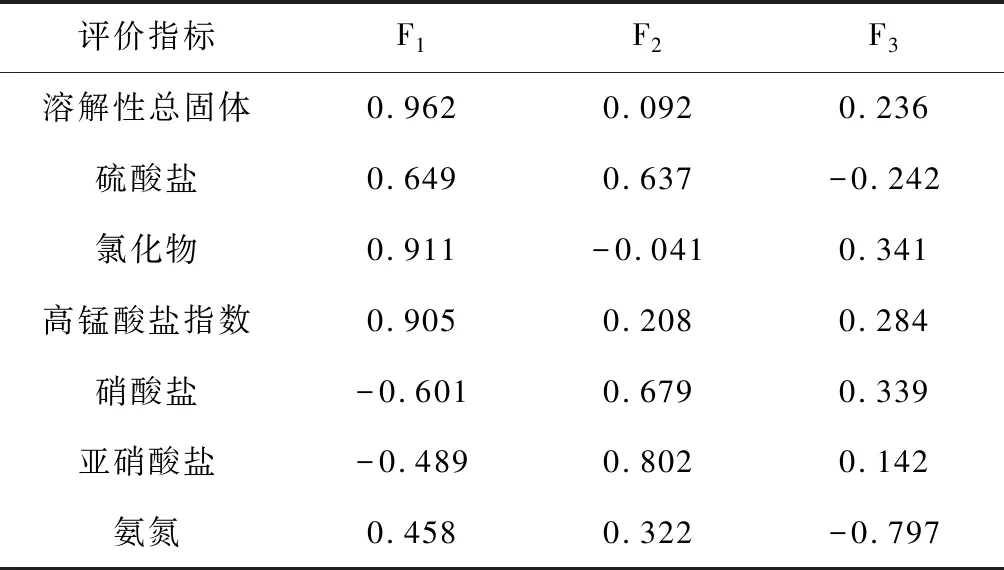
表5 主成分初始因子载荷矩阵

第一主成分F1：在F1具有较高载荷的主要水质指标为溶解性总固体(0.962)、氯化物(0.911)、高锰酸盐指数(0.905)、硫酸盐(0.649)，其方差贡献率达54.373%，是区内的主要影响因子。氯化物主要来源于海水入侵；高锰酸盐指数主要来自于生活和工业排放的废水；硫酸盐主要来源于工业排放的废水；溶解性总固体与氯化物、高锰酸盐指数具有较强的相关关系，溶解性总固体会随着氯化物、高锰酸盐指数浓度的增高而一同增高。F1属于海水入侵、生活和工业等综合污染因子。

第二主成分F2：在F2具有较高载荷的主要水质指标为硝酸盐(0.679)、亚硝酸盐(0.802)，其方差贡献率达23.812%。硝酸盐、亚硝酸盐主要来源于农业生产使用农药化肥、生活污水、 生活垃圾等，F2属于农业生活污染因子。

第三主成分F3：在F3具有较高载荷的主要水质指标为氨氮(-0.797)，其方差贡献率达23.812%。氨氮主要来源于农业生产使用农药化肥、生活污水、 生活垃圾等，F3属于农业生活污染因子。

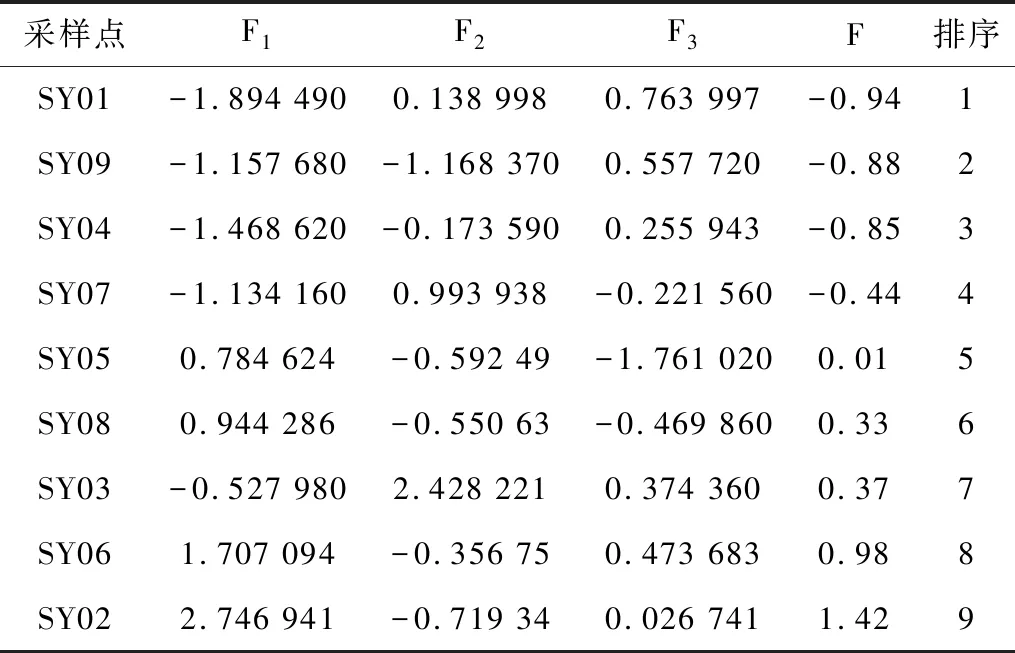
表6 F值综合得分

2.5 主成分表达式建立及水质评价

各个主成分的得分Fi由标准化处理后的数据ZXi乘以每个指标对应的系数K确定，每个指标对应的系数K由主成分初始因子载荷矩阵系数除以主成分对应特征值平方根得到，各个主成分得分表达式为：

F1=0.493 106ZX溶解性总固体+0.332 667ZX硫酸盐+0.466 965ZX氯化物+0.463 889ZX高锰酸盐指数

F2=0.525 899ZX硝酸盐+ 0.621 164ZX亚硝酸盐

F3=-0.766 204ZX硝酸盐

由各个主成分表达式及特征值λ1=3.806、λ2=1.667、λ3=1.082确定综合水质评价函数[9-11]：

F=[λ1/(λ1+λ2+λ3)] F1+[λ2/(λ1+λ2+λ3)] F2+[λ3/(λ1+λ2+λ3)] F3=0.580 625F1+0.254 310F2+0.165 065F3

由上述公式，计算得到研究区9个采样点的主成分得分和综合得分，结果见表6。依据综合得分的大小定量描述水质的污染程度，综合得分越高，水质污染越严重，由此可对采样点水质进行排序，由优至劣为SY01>SY09>SY04>SY01>SY07>SY05>SY08>SY03>SY06>SY02。

3 结语

本研究以福建某滨海场地地下水为研究对象，选取7个水质指标运用主成分分析法进行分析，得到综合水质评价函数，对水质进行评价。

(1)运用主成分分析法可以将7个水质指标综合为3个主成分进行解释，累积方差贡献率为93.648%，第一主成分的方差值54.373%较大，第二主成分的方差值23.812%和第三主成分的方差值15.462%相对较小，说明影响水质的污染源具有复杂多样性的特点，3个主成分包含了原始数据的大多数信息，可利用他们来评价地下水水质。

(2)分析初始因子载荷矩阵系数结果显示：主成分F1控制指标为溶解性总固体、硫酸盐、氯化物、高锰酸盐指数；主成分F2控制指标为硝酸盐、亚硝酸盐；主成分F3控制指标为氨氮。

(3)通过确定综合水质评价函数计算得到各个采样点水质综合得分，对水质进行综合评价，水质由优至劣顺序为SY01>SY09>SY04>SY01>SY07>SY05>SY08>SY03>SY06>SY02。