COSINE系统分析程序并行耦合计算研究

胡硕文，林 萌*，刘 京，陈冠宇

(1. 上海交通大学核科学与工程学院，上海 200240；2. 国家电力投资集团科学技术研究院有限公司，北京 100029；3. 中国核动力研究设计院，四川 成都 610213)

1 引言

全范围模拟机可以用于仿真核电站运行过程，并对核电站的事故工况进行安全分析[1-3]。全范围模拟机是培训核电站的操纵员的关键设备，同时也是核电站的标准配置，准确性和实时性是其关键参数[4]。当模拟机中的单一仿真模型节点庞大时，会导致程序计算速度变慢影响实时性，开展并行计算研究以提高其计算速度具有重要的工程意义。

热工水力仿真程序是开发全范围模拟机的基础，国外在该方面起步早，现已研发了多个知名的热工水力计算程序。例如，轻水堆系统的瞬态分析最佳估算程序RELAP5可以模拟两相流，用于全范围模拟机模型开发，是核电厂分析的重要工具[5]。陈俊杰等针对换热问题，基于RELAP5程序，使用壁面温度作为耦合参数，研究了热构件壁面温度耦合并行技术，提高了计算速度[6]。但是，目前针对国产自主化的核电厂热工水力仿真程序并行计算的研究较少。

为提高全范围模拟机的计算速度，并促进我国核电热工水力仿真程序的发展，本文使用具有我国自主知识产权的COSINE(COre and System INtegrated Engine for design and analysis)软件包里的cosSyst(系统分析程序)[7]，进行了热工模型搭建，通过并行计算，缩短了计算时间，全范围模拟机更容易满足实时性的要求。

2 流体热工水力基础方程

在全范围模拟机中，热工水力程序并行耦合计算通过子系统间的参数传递实现。典型的传递方法如下，在耦合时刻和物理空间耦合节点处，一方面，子系统A通过流体热工水力基础方程将计算的内部节点参数传递给子系统B用于更新子系统B的边界参数；另一方面，子系统B在接收更新的边界参数后，同样调用流体热工水力基础方程完成求解后，也将子系统B的内部节点参数传递给子系统A用于更新子系统A的边界参数；依此往复，实现热工水力程序并行耦合计算。因此，具体耦合的参数依赖于所选用热工水力程序的基础方程。

本文使用的是cosSyst程序，其采用一维瞬态非热平衡非力平衡的两流体模型，基于半隐式差分离散格式，求解基础变量压力、液相焓值、气相焓值、液相速度、气相速度和空泡份额等。

流体在封闭空间内流动，满足质量守恒，即

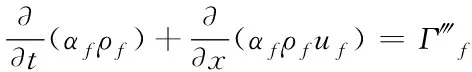
(1)

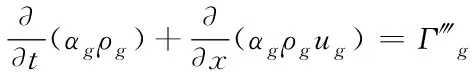
(2)

在计算过程中，流体满足能量守恒，即

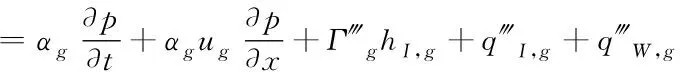
(3)

(4)

另外，流体保持动量守恒，即

+Γ‴fuI+F‴I，f+F‴W，f+F‴L，f

(5)

+Γ‴guI+F‴I，g+F‴W，g+F‴L，g

(6)

式中，下标f是液相，下标g是气相，α是空泡份额，ρ是密度，u是速度，Γ‴是由于相变的质量生成率，p是压力，g是重力加速度，θ是控制体与竖直方向之间的夹角，F‴I是相间摩擦力，uI是相界面速度，F‴W是壁面摩擦力，F‴L是局部阻力，h是焓，hI是相界面焓，q‴I，f是相界面传到液相的热流，q‴I，g是相界面传到气相的热流，q‴W，f是壁面传到液相的热流，q‴W，g是壁面传到气相的热流，t是时间，x是距离。

压力、两相焓值、两相流速与空泡份额是上述方程重要的因变量，因此选择压力、焓值、质量流量与空泡份额作为模型耦合参数。

3 耦合方案

模拟机热工水力建模使用的基本模块包含管道、阀门和加热器等模块，由多种模块组成复杂的热工水力系统。cosSyst在求解模块的热工参数时，都是使用上述方程进行求解，求解原理是相同的。因此，本文以管道、阀门和加热器为基础建立简单模型，验证耦合方案在cosSyst的适用性。模型拆分前为整体模型，将模型进行拆分得到的两个模型为耦合模型。整体模型如图1所示，耦合模型如图2所示。部件#1、#5、#6与#10为边界，部件#2与#9模拟由5个控制体组成的管道，部件#3与#8模拟阀门，部件#4与#7模拟单控制体管道，部件#11模拟加热器。

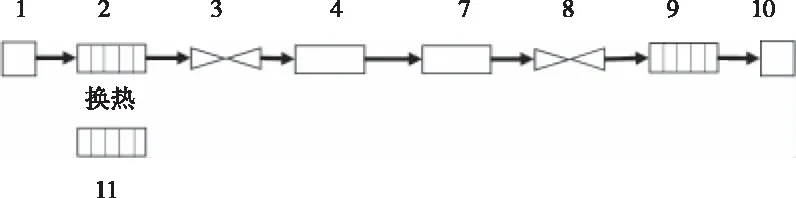
图1 整体模型节点

耦合模型之间通过传递参数进行耦合，计算时间每过100毫秒(设置的同步周期)上游模型与下游模型的压力P、焓值h、空泡份额α和质量流量F会通过数据库进行数据交互，耦合方案如图2所示。

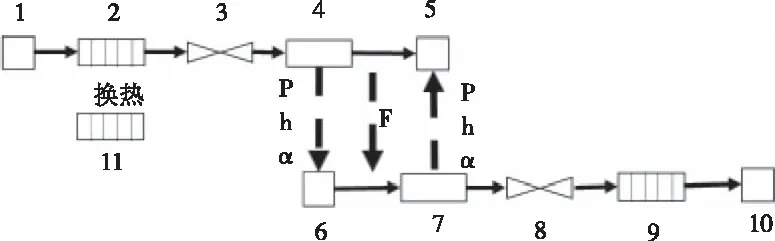
图2 耦合模型节点

在核电厂流体系统中，流体存在单液相、单气相与两相这三种典型状态，故本文对整体模型与耦合模型在上述三种流体状态下仿真，对比整体模型与耦合模型的参数偏差。同时，并行耦合计算的热工水力程序需要在稳态工况下和瞬态工况下均能得到准确的计算结果，测试将覆盖稳态和瞬态工况。针对图1和图2所示的热工模型，在达到稳定计算的基础上，调节阀门#3的开度。在50至60秒期间，阀门开度由0.5线性降至0.25；在200至210秒期间，阀门开度由0.25线性升至0.5，阀门#3开度变化如图3所示。通过调节阀门开度改变局部阻力造成流体流速与压力场分布变化，以制造典型的瞬态工况。

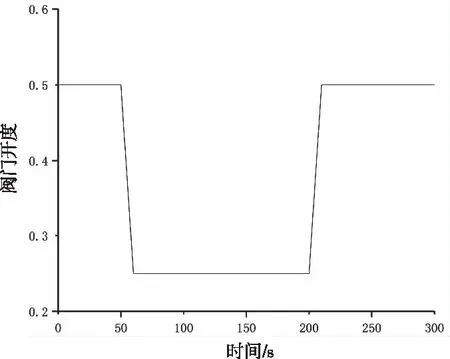
图3 阀门#3开度随时间变化

4 数值计算分析

为研究耦合方案的适用性，本文选取了耦合处的管道#4和管道#7的质量流量、压力、温度，将耦合模型与整体模型的上述参数分别在初始稳态40秒时刻、中间稳态190秒时刻、最终稳态300秒时刻及0-300秒过程内进行对比。

4.1 单液相流体耦合

单液相流体为过冷水，设置入口边界#1压力为7.0 MPa，液相比焓为1214 kJ/kg，设置出口边界#10压力为6.8 MPa。

在50秒时刻，由于阀门开度减小，质量流量减小，故管道#4和#7温度开始升高。在200秒时刻，由于阀门开度增大，质量流量也增大，故管道#4和#7温度开始降低，最终恢复至初始状态。节点质量流量、压力和温度如图4、图5和图6所示，参数偏差如表1所示，其中，F代表质量流量，P代表压力，T代表温度。从表1可以看出，稳态下单液相流体的整体模型和耦合模型之间的偏差不超过0.2%，整个仿真过程内最大偏差不超过2%。

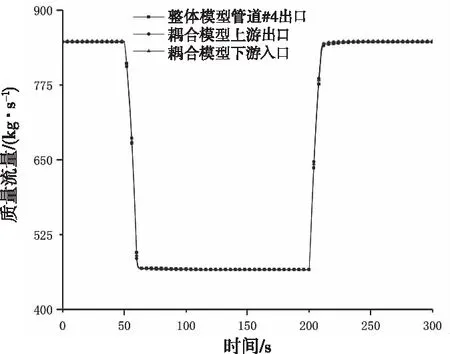
图4 节点质量流量

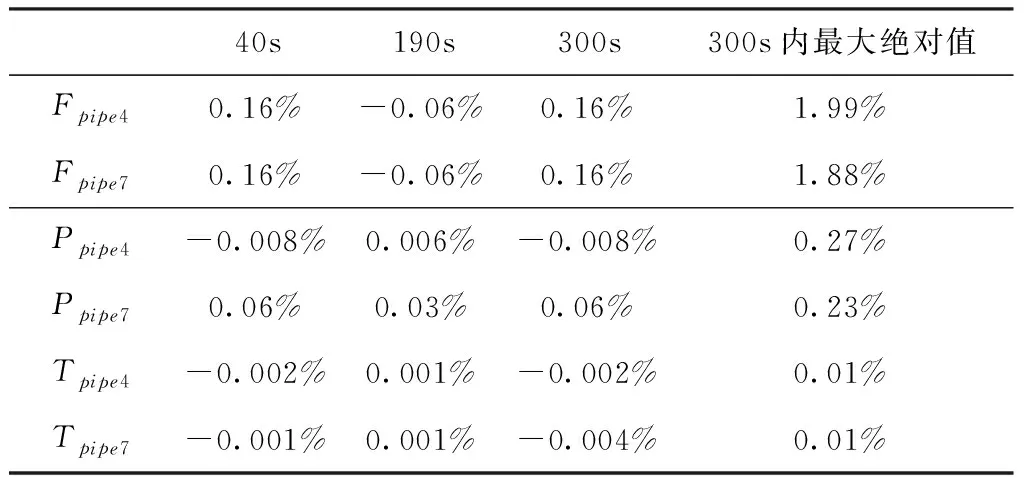
表1 单液相流体整体模型与耦合模型参数偏差

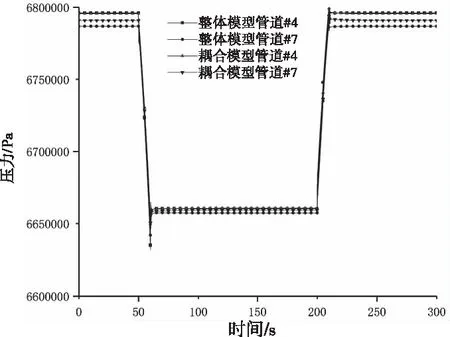
图5 节点压力

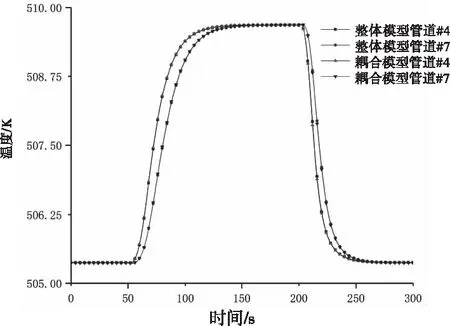
图6 节点温度

4.2 单气相流体耦合

单气相流体为过热蒸汽，设置入口边界#1压力为6.0MPa，气相比焓为2975kJ/kg，设置出口边界#10压力为5.6MPa。

质量流量、压力和温度仿真结果如图7、图8和图9所示，参数偏差如表2所示。从表2可以看出，稳态下单气相流体的整体模型和耦合模型之间的参数偏差不超过3%，整个过程偏差最大不超过4%。

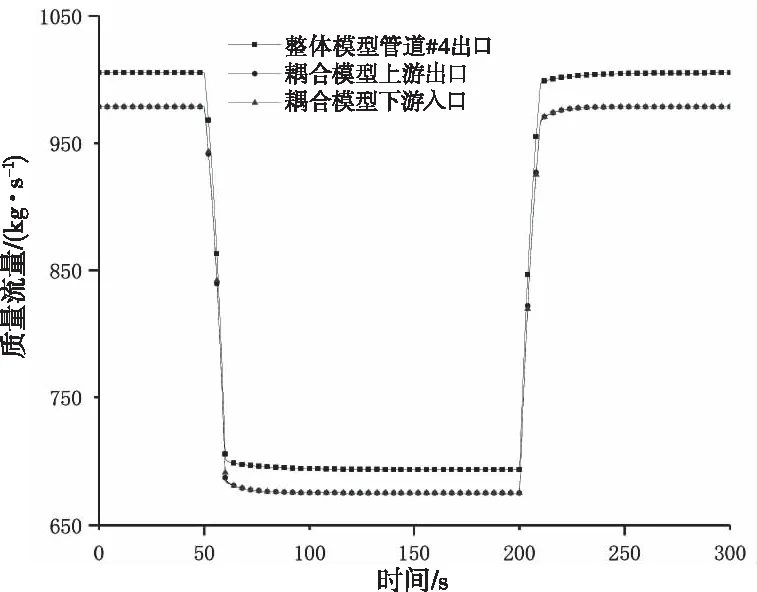
图7 节点质量流量

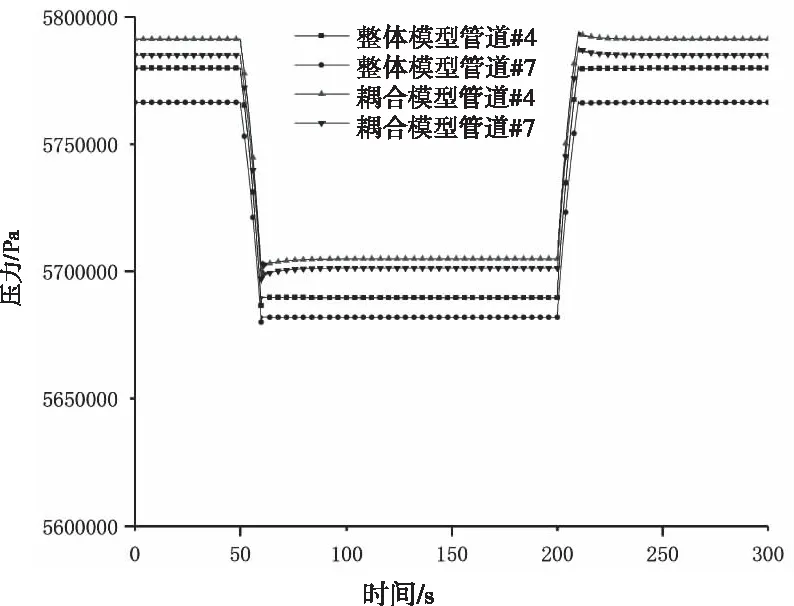
图8 节点压力

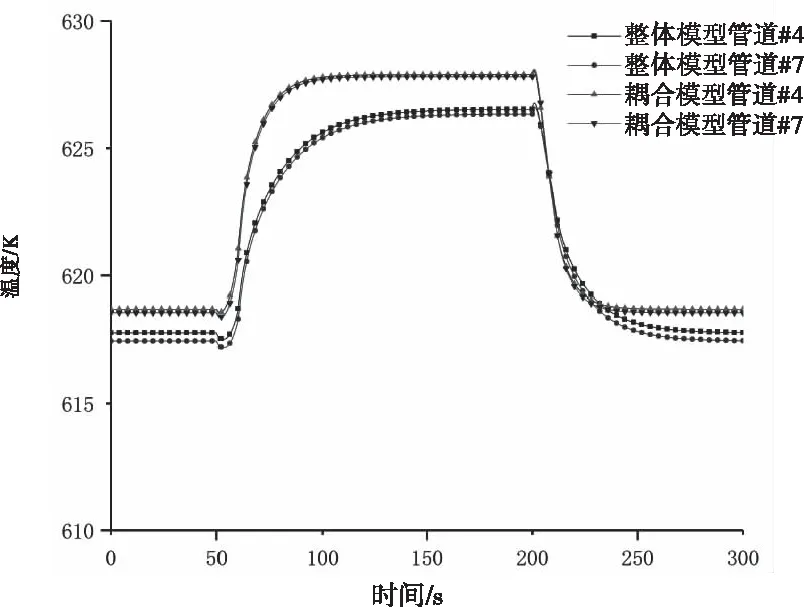
图9 节点温度

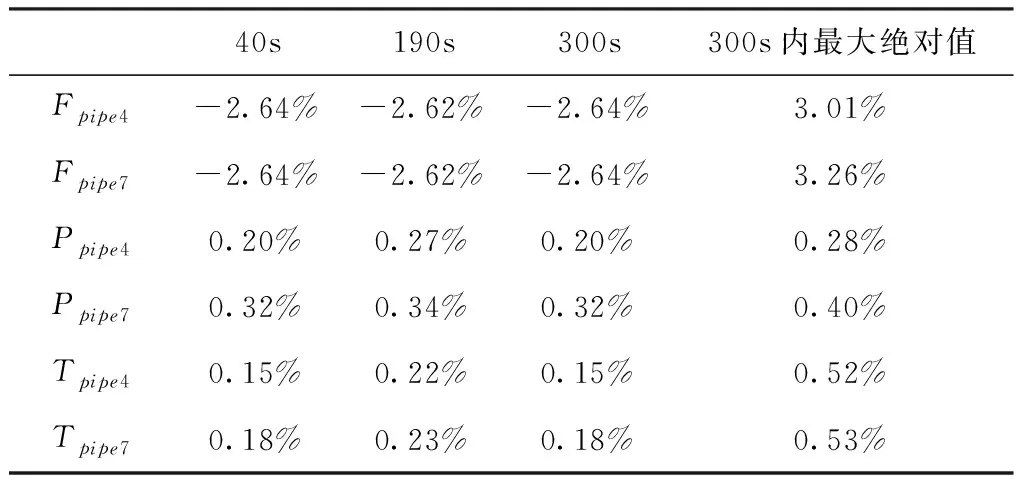
表2 单气相流体整体模型与耦合模型参数偏差

4.3 两相流体耦合

流体为饱和水与饱和蒸汽的混合物，设置入口边界#1压力为6.0MPa，液相体积份额为0.5，气相体积份额为0.5，设置出口边界#10压力为5.6MPa。

质量流量、压力和温度仿真结果如图10、11和12所示，参数偏差如表3所示。管道#4和#7压力降低，故管道#4和#7温度出现了下降趋势。从表3可以看出，稳态下两相流体的整体模型和耦合模型之间的参数偏差不超过3%，整个过程偏差最大不超过6%。

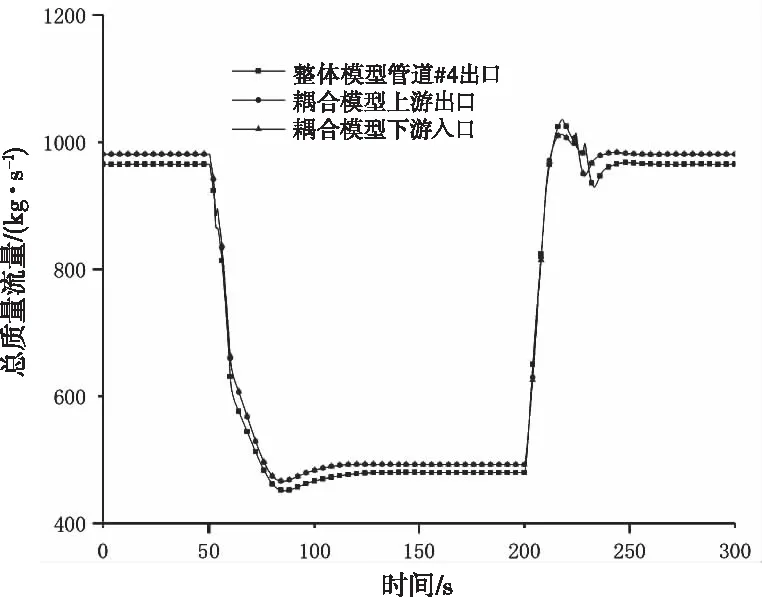
图10 节点总质量流量

图11 节点压力

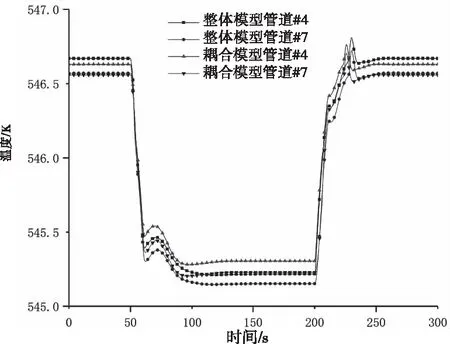
图12 节点温度

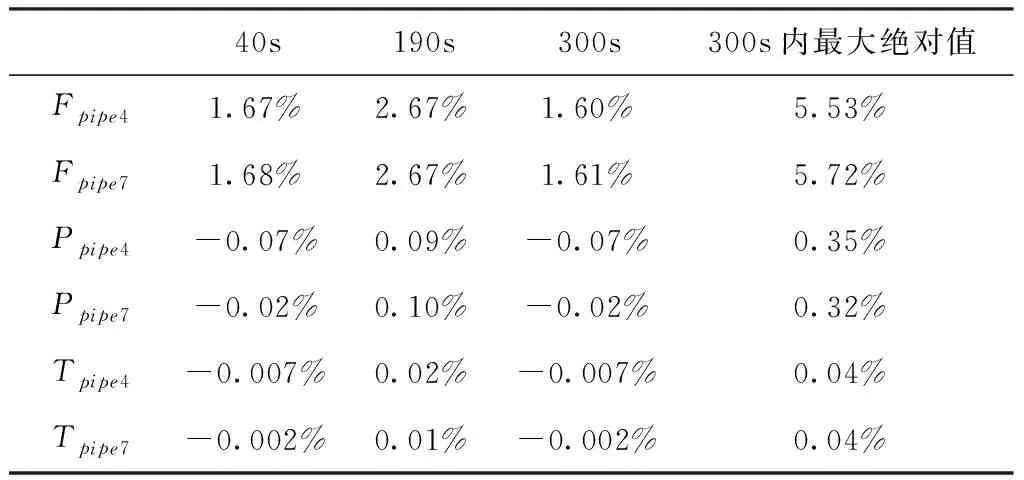
表3 两相流体整体模型与耦合模型参数偏差

单液相、单气相与两相模型仿真300秒的CPU计算消耗时间如表4所示。由表4可以看出，将模型拆分为耦合模型，通过并行计算可以缩短CPU计算消耗时间，提高计算速度。

表4 CPU计算消耗时间

4.4 耦合方法适用性理论分析

本文所采用的耦合方案实质是基于热工水力程序基础守恒方程的一种边界值动态显式耦合方法，通过不断传递和修改不同热工水力系统边界上的参数值实现。即，被计算的热工水力系统的边界值在本计算时间步长内保持不变，该边界值由另一热工水力系统在前一耦合时刻根据计算动态确定。根据原理分析，此种耦合方法对于系统内部的节点数或系统运行状态的改变并无依赖。因此，理论上该方法既适用于小节点规模，也适用于大节点规模的热工水力模型，既适用于稳态或瞬态计算，也适用于事故工况计算。值得注意的是，此种耦合方法由于采用显式耦合方式，耦合频率对耦合计算结果有影响。对于参数变化剧烈的过程(参数变化响应时间与耦合周期相当，一般为0.1s)，如果耦合频率过低，可能会造成模型参数计算震荡。

在上述耦合方案基础上，针对热工水力模型，本文以简单对象为例进行了三种典型算例计算，包括单相液、单相气和气液两相。对于两流体的热工水力程序而言，虽然本文采用的对象简单，但从计算节点守恒方程的角度进行了全覆盖，同时也测试了方程中所涉及的热工水力参数的主要状态。相较于全范围模拟机更复杂的热工水力系统模型、更多的计算节点和状态，其计算方法和原理与本文的简单对象模型是完全一致的。因此，理论上本文所采用的耦合方法可推广至全范围模拟机的热工水力模型耦合中，此适用性在目前已开展的全范围模拟机热工水力建模与耦合中得到了部分证实。

5 结论

全范围模拟机模型庞大时计算速度会下降，难以达到实时仿真。为此，将整体模型进行拆分，采用耦合方案进行模型耦合，通过并行计算仿真了模型在单液相流体、单气相流体和两相流体下的工况。通过整体模型与使用并行计算的耦合模型之间的节点参数对比，得到如下结论：

1)整体模型与耦合模型的参数在稳态下的最大偏差不超过3%，瞬态下最大偏差不超过6%。

2)通过并行计算，CPU消耗时间节省了18%以上，计算速度得到了提高。

3)本文所采用的耦合方案适用于全范围模拟机的模型耦合，有利于全范围模拟机实现实时模拟。