一种通信网拓扑脆弱性评估算法设计与仿真

刘赟宇，徐 晟

(天津中德应用技术大学软件与通信学院，天津 300350)

1 引言

通信网络通常作为电力、交通等系统的支撑网络，如果某部分出现故障，就会导致信息丢失或传输中断，影响系统正常运行。随着通信系统的智能化发展和通信规模的不断扩大，网络拓扑结构越来越复杂，业务承载量也随之增加，其中一些通信业务呈现出星形结构，对信息传输的实时性和可靠性提出更高要求。为加强通信系统安全保障，网络拓扑脆弱性评估尤为重要。拓扑脆弱性表示某个或集群信息资产具有被攻击的可能，是因硬件或软件等方面管理不当导致的缺陷，违背安全策略，容易造成通信安全事故。

为合理评估拓扑脆弱性，相关学者提出如下解决方案。文献[1]建立力学模型完成通信网络脆弱性评估。将业务数据往来占有的带宽容量和节点业务往来数量称作节点相关性；在统计业务时利用均分时隙的最大似然估计，并以松柏过程为统计背景明确估计参数，通过节点之间的逻辑距离判断网络拓扑是否存在脆弱性。除此之外，还有学者利用基于社团结构的方式评估通信网的脆弱性。以某地区通信网络为例，探究该网拓扑最短路径，结合网络内部构造，将其划分为多个子区域，建立可靠性评估模型，若可靠度较低，则表明具有脆弱性。

上述方法为通信网脆弱性评估提供了有效工具，但是当网络结构极其复杂时，难以获得准确的评估结果。因此，本文基于分形机理评估通信网拓扑结构的脆弱性。分形一词由古希腊学者提出的，原意指不规则的意思。分形机理就是将非规则几何形态当作研究目标的几何学，其具备一些自相似性[2，3]，通常情况下分形维数高于其拓扑维数。通信拓扑分形模型，能选取最佳评估指标，确立评价函数，得出精准的评估结果。

2 基于分形机理的通信网拓扑脆弱性评估

2.1 通信网拓扑分形模型构建

建立通信网络拓扑模型时，需将整个通信网络看作一个有权无向网络[4]，且不考虑节点和配线架等设备。假设通信网络中共包括N个节点和M条边，共同形成有权网络G=(V，E)，其中V={v1，v1，…，vN}代表节点集合，E={eij}为边集合。建立的通信网络连接矩阵[5]如下：

A={aij}⊂RN×N

(1)

如果节点i和j间存在连接，表示为aij=1，反之aij=0。构建的节点权重矩阵如下：

W={wij}⊂RN×N

(2)

公式中，R代表集合元素。

由上述可知，在通信网络中，任意两个节点间均存在业务关联性，将此种特征记作Fij，其计算公式如下

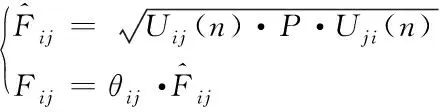
(3)

式中，θij代表修正系数，Uij(n)描述两节点间的业务数量，P表示节点间余弦相似度。

已知节点间连接情况和业务相关性，基于分形机理的关联特征建立通信拓扑传输模型。分形维数[6]的计算公式如下

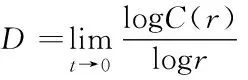
(4)

式中，C(r)代表分形体s和t两个点间距，也可以记作dst，其计算公式如下

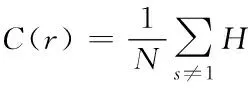
(5)

式中，r表示分形半径，dst与r之间存在下述关系

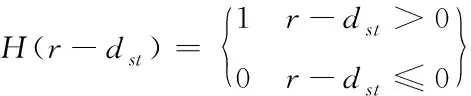
(6)

通信网络是由多个节点汇聚形成的，汇聚节点一般具备较强的数据计算能力，能够有效处理汇聚信息[7]。在层级分明的路由协议中，将子网络集团称作簇，许多很小的簇能构成大簇，该性质满足通信网络分形结构特性，也就是自相似性特征。

当通信网络的结构较为简单时，上述分形维数计算公式可直接使用，但当网络非常复杂时，需结合分形机理提出盒维数计算方法。假设将边长是LB的盒子作为分形体，盒子数量表示为NB(LB)，此处“盒”的概念表示其维度，如一维表示长度是LB的线段，二维则描述长度是LB的矩形，盒维数表达式如下

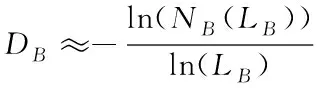
(7)

在建立拓扑模型时，可结合网络节点分布特征[8]，利用盒维数准确体现出参与通信的节点和网络结构。详细步骤如下

将通信网络区域分割成N′个子区域Si(i=1，2，…，N′)，假设每个小区域均为正方形，边长是l。在设置节点位置时，忽略节点物理尺寸[9]，节点在区域Si内的几率为pi。通过测度指数[10]di描述

pi≈ldi(i，1，2，…，N′)

(8)

如果子区域面积产生变化，即当l改变小时，子区域数量就会增多，上述公式可转换为以下形式

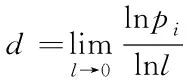
(9)

利用上述方法将通信网络划分为若干个子区域，选取每个区域中的传输节点，确定拓扑传输架构，更有利于分析网络拓扑的脆弱性。

2.2 评估指标选取

1)节点连接紧密度

通常利用富者俱乐部系数[11]来表示节点之间的连接程度，计算公式如下

Φ(r′/n)=2L/r′(r′-1)

(10)

式(10)表达的含义为：前r′个紧密度最大的节点间，真实存在的边数L和可能存在的边数r′(r′-1)之间的比值。若有Φ(r′/n)=1，则这些节点可以建立一个完整的连通图。富者俱乐部指数表现出节点的小团体结构，若该指数太低，网络结构不稳定，过高容易造成流量集中，具体适应度值应根据网络实际情况确定[12]。

2)网络结构有序度

熵是描述网络节点有序性的指标，针对任意已知序列的概率分布[13]{p1，p2，…，pk，….，pn}，都可以获得与其相对的熵表达式

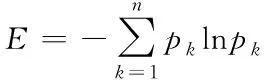
(11)

如果序列概率均一致，即pk=1/n，则最大熵表示为lnn。

评估通信网络脆弱性时，可同时计算网络中节点、链路的熵值，评估它们的分布是否有序。

例如计算通信网结构熵时，假设n为节点总数，ki是第i个节点度，则该节点的重要程度计算公式如下

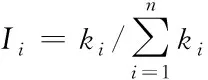
(12)

将(I1，I2，I3，…，IN)当作分布序列，就能够计算出网络结构熵

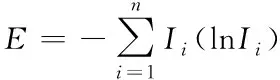
(13)

因此，能够获得网络有序度

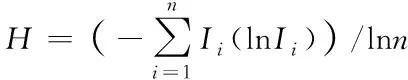
(14)

3)节点中心化程度

通过节点度描述中心化程度[14]，该指标表示节点具有的邻居节点数量，邻居节点越多，表明中心化程度越高。假设任意一节点度是K的几率表示为

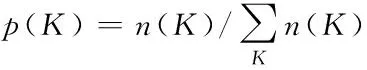
(15)

式中，n(K)表示节点度是K的节点数量，p(K)值越高，表明节点中心化程度越高，重要节点越多。

4)链路介数

介数是反映通信网络流量是否异常的指标。假设链路eij的介数表示为βeij，其代表此条链路作为整个网络最短链路的比例，计算公式为

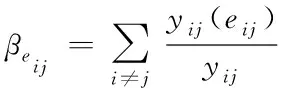
(16)

式中，yij代表节点i和j存在的最短路径。

5)传输延时

已知通信网络传输的时间序列为

X=[x1，x2，…，xn′]T

(17)

利用自相关函数获取xi′与xi′+τ的相关性，即可获得网络传输的延迟时间τ，自相关函数表达式如下

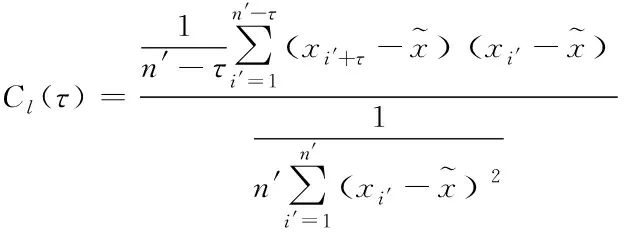
(18)

2.3 脆弱性评估函数确立

基于以上评估指标，构建如下脆弱性评估模型。在通信过程中，会根据选择的路径传输信息，通过的链路越少，通信成功率也就越大。因此，在通信拓扑分形网络基础上计算两节点的路由集合和所有路径包含的链路数量，进而能够得到经过第α条路径的几率ρα。

已知i和j两个节点的路由集合表示为φij，共包含g条路径，且每条路径中含有z条链路，则通信选取第α条路径的几率表示为

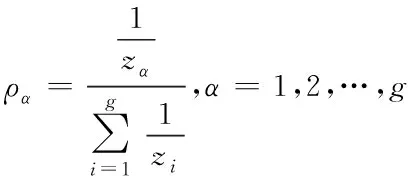
(19)

上述公式符合以下条件

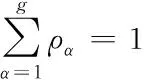
(20)

确定传输路径后，假设利用该路径完成通信，在此情况下评估整体网络的脆弱性，确立下述评价函数。

在物理拓扑与业务双重约束下[15]，建立能效函数E(G)，获取最终网络脆弱性综合评估结果。物理拓扑方面效能函数为

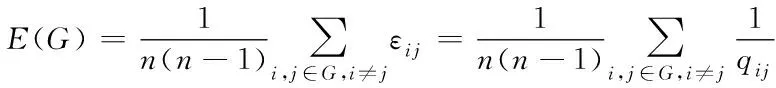
(21)

式中，εij代表不同节点间通信效率，并和通信最短距离存在反比关系，即εij=(1/qij)。当qij=∞时，εij=0。

针对通信网业务而言，网络能够承载的数量和种类是一定的，如果因去除某节点或某边造成业务失效，说明网络具有一定脆弱性。综合物理层与业务层得到下述评估通信网络拓扑性能的综合指标GNP(G)

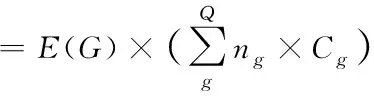
(22)

式中，Cg代表业务类型是g的重要程度，Q表示业务种类。

3 仿真数据分析与研究

仿真以某市电力通信网络为目标，网络拓扑结构如图1所示。所有链路带宽都设置为50Mbit/s，该通信网络包括的业务类型有：安稳业务、电话调度、视频会议、数据调度、不同级别信息传输业务。每种业务的重要程度均不同，且各链路带宽设置为50Mbit/s。

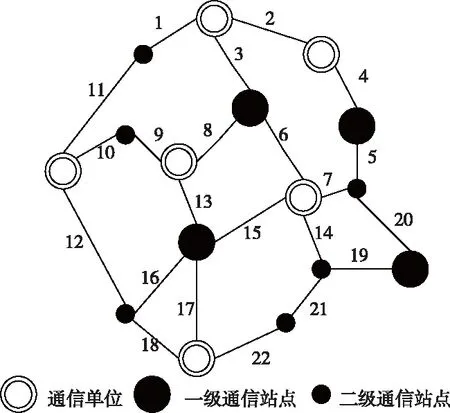
图1 仿真目标通信拓扑结构图

仿真平台整体架构如图2所示。

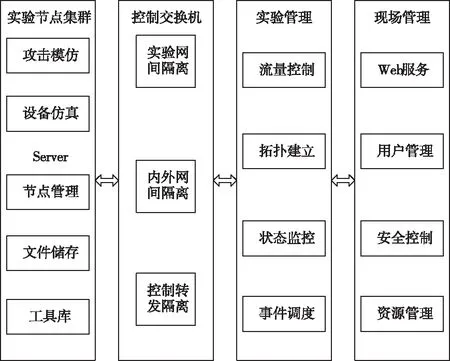
图2 仿真平台整体结构图

仿真平台由以下设备构成：

交换机：主要任务是连接所有控制系统，提供内外网隔离等服务，是整个平台的支撑；

通信节点：是仿真终端，能够展现设备仿真模型，可建立实验容器环境；

Boss Server：主要负责用户管理、资源管理、状态监控等工作，还能控制交换设备；

服务器：控制无线设备；

OPS Server：可实现信息储存、传输、共享等功能；

AC/AP：管理通信协议，包括Fit AP以及Fat AP。

首先，只针对图1所示的通信网拓扑，分析不同攻击模式下各链路的脆弱性。假设不同攻击模式所选择的链路情况如下：

随机攻击：链路集合为{1，3，4，8，13，17，22，18}；

高阶数攻击：链路集合为{2，4，5，20，19，14，6，8}；

高压力攻击：链路集合为{12，16，15，7，5，4，2，1}；

高脆弱性攻击：链路集合为{9，8，6，14，19，20，5，7}。

在上述仿真环境中，基于分形机理分析不同攻击模式下通信网拓扑的脆弱性，实验结果如图3所示。

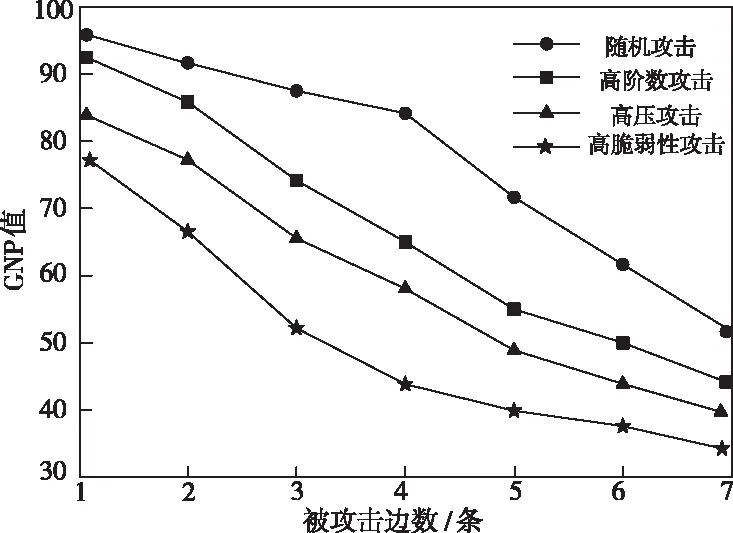
图3 不同攻击模式下网络脆弱性对比

针对上述四种攻击模式，攻击强度排序情况为高脆弱性攻击>高压攻击>高阶数攻击>随机攻击。由图3可知，随机攻击模式下脆弱性评估结果的GNP值最高，表明网络综合性能良好，脆弱性特征较弱，但随着被攻击边数的增多，脆弱性逐渐增强，其它模式下的脆弱性评估结果和实际情况相符，其中高脆弱性攻击对网络造成的危害最大，因此今后需对此种攻击类型加以防范。

上述是针对一个网络中不同攻击模式下的脆弱性评估，下面对于三种不同静态网络的利用所提方法完成脆弱性评估。假设所有网络被攻击的速率是600pps，且每五个评估指标所占权重相同，分析不同网络的脆弱性指标，如表1所示。

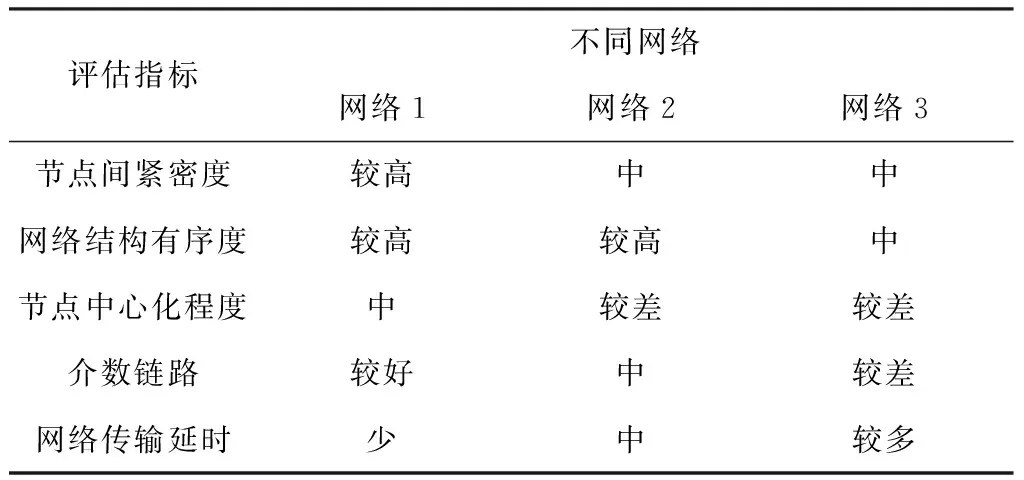
表1 不同网络的脆弱性评估结果表

结合表1的脆弱性指标分析结果，通过GNP值描述三种不同网络的综合评价结果，如图4所示。

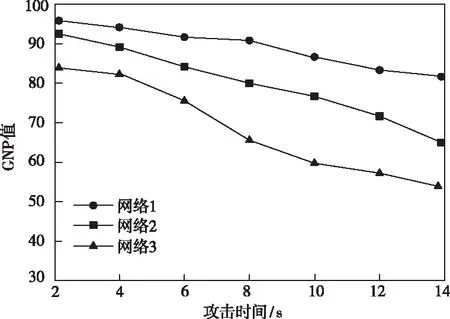
图4 不同网络脆弱性评估结果

图4显示，通信网络1的GNP值最高，其次是网络2和网络3。该评估结果和表1显示的不同网络各项指标评估结果相符，其中网络1的综合性能最好，因此其没有表现出较强的脆弱性，GNP值始终保持在较高水平。这是因为本文利用分形机理建立了通信网络拓扑传输模型，更加准确描述出参与通信的链路和节点，有利于全方面评估网络脆弱性，提高评估结果精度。

4 结论

面对复杂的通信系统，网络脆弱性始终是阻碍通信发展的关键问题。本文围绕分形机理开展通信网络拓扑脆弱性评估。基于分形技术的关联特征，建立通信网传输模型，准确描述参与通信的链路与节点，将节点紧密度、中心化程度以及传输延时情况等作为评估指标，构建评估函数，得出最终评价结果。仿真结果表明，分形机理适用于网络脆弱性评估，得到的结果和符合网络实际状态。在下一步研究工作中，应结合信息论与控制论等内容，针对通信网络展开更加深入的评估。