基于近似消息传递的VLC非线性均衡器

刘 希，苗 圃*，姚 誉

(1. 青岛大学电子信息学院，山东 青岛 266071；2. 华东交通大学信息工程学院，江西 南昌 330013)

1 引言

无线通信系统由于频谱资源的紧缺而面临较大的发展限制。可见光通信(VLC，Visible Light Communication)系统以其无需授权的光频段、成本低、信息安全性高和空间复用性高等优点[1]吸引了诸多研究者的目光。但是VLC系统中存在严重的非线性失真，主要源于发光二极管(LED，Light Emitting Diode)的非线性特性，其影响系统整体性能的提升。为了满足VLC系统传输正实数单极性信号的要求，调制方式之一直流偏置-正交频分复用(DCO-OFDM，DC-biased Optical Orthogonal Frequency Division Multiplexing)应用较为广泛。但是DCO-OFDM信号不仅具有较高的均峰比，且对LED的非线性特性非常敏感[2]，所以补偿LED非线性失真对DCO-OFDM有效的数据传输非常重要。目前非线性失真补偿大致分为预失真补偿技术和后失真补偿技术[3]，其中基于后失真补偿技术的非线性均衡器由于具有较好的非线性补偿性能而应用较为广泛[4-6]。

均衡器是根据传输信道的逆特性构造非线性功能模块，并将其放置在接收端，对LED非线性和无线多径信道进行补偿，进而达到提升系统数据传输性能的目的。均衡器行为模型多以沃尔特拉级数(VS，Volterra Series)为基础建立，但是VS结构复杂，内核个数随着非线性阶数和记忆深度呈指数增长，增加了内核参数计算难度。因此降低计算复杂度、提高计算精度成为VS内核参数提取的关键问题。

压缩感知(CS，Compressed Sensing)是一种有效的稀疏重构方案[7-8]，重构算法是CS的核心。CS的可行性要求重构信号在变换域中是稀疏的或本身是稀疏的，且观测矩阵应满足有限等距性质(RIP，Restricted Isometry Property)。而基于VS的非线性后失真均衡器(VS-NPE，Volterra Series-Nonlinear Post-distortion Equalizer)满足上述条件，证明CS可用于VS-NPE内核参数提取[9-10]。AMP[11]是一种高效的CS重构算法，它不需要复杂的矩阵求逆，具有计算复杂度低、重构精度高的优势。然而，它在VS-NPE内核提取的应用中也具有局限性，因为AMP算法的有效性需观测矩阵满足独立同分布(i.i.d，Independently Identically Distribution)的条件，但VS-NPE的观测矩阵有高度的列相关性，因此无法直接使用AMP算法进行VS-NPE内核参数提取。

在文献[12]-[14]工作的基础上，本文提出一种基于支持集修正的AMP(SSR-AMP，Support Set refined Approximate Message Passing)算法来计算VS-NPE内核参数。算法首先修正内核参数观测矩阵以降低其列间相关度，然后通过引入阻尼技术改进AMP算法的迭代过程；在得到可靠支撑集基础上，最后采用LS计算VS-NPE内核参数。所提方案可以克服AMP算法无法直接用于VS-NPE内核参数计算的缺点，并提高VS-NPE内核参数辨识性能。

2 基于后失真均衡器的VLC系统

2.1 LED模型

当输入电压小于开启电压时，LED会进入截止区，电流不导通。为了让LED工作在有效范围区，需加直流偏置，但会导致输入电压幅度过大，使LED进入非线性工作区，进而展现显著的非线性特性。另外，由于载流子密度的响应受频率影响，通带内不平坦的频率响应又会引入LED的记忆效应[15]。因此，借助Wiener模型对LED的传输特性进行建模，该模型由线性时不变(LTI，Linear Time Invariant)模块和非线性(NL，Nonlinear)模块组成[15]。LTI模块可表示为

y(n)=exp(-2πnfc)

(1)

(1)式中，fC=20MHz为截止频率。根据商用LED(Cree PLCC4)的测量，NL模块可由一个三阶多项式来描述，建模为

f(n)=0.2855y3(n)-1.0886y2(n)

+2.0565y(n)-0.0003

(2)

取最小开启电流Imin=0.1A、最大前向电流Imax=1A、直流偏置IDC=0.4A。实际的LED具有单向导电性和非线性，建模后的LED设置最大前向电流和直流偏置，使LED工作在有效工作区。

2.2 VLC信道模型

参考IEEE 802.11协议的室内可见光光多径信道模型搭建以视线传输(LOS，Line of sight)为主的信道模型，其信道脉冲响应(CIR，Channel Impulse Response)可表示为

(3)

其中，Pn是第n射线的光功率，τn是第n射线的传播时间，δ(t)是狄克拉函数，Nr是探测器接收到的射线数量。利用均方根延迟扩展来量化hNr的时间分散特性，计算表达式为

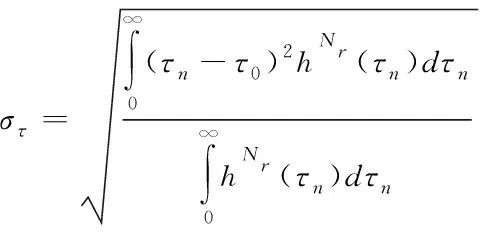
(4)

式中的平均延迟扩展τ0可由下式计算得

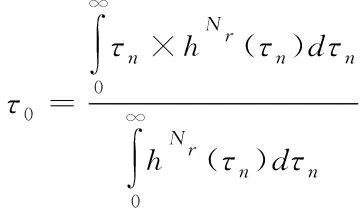
(5)

假设RPD为响应度，则可以将PD的冲激响应建模为

hPD(n)=RPDδ(n)

(6)

z(n)=RPDf{(x(n)+IDC)*y(n)}*hNr+e(n)

(7)

其中*表示卷积运算，而e(n)表示信道噪声，RPD取值为1。

2.3 后失真均衡器行为模型

本篇采用VS建立后失真均衡器模型。VS等效于向泰勒级数添加记忆项，它是用于非线性系统的通用功能模型，可以较高精度地逼近任意非线性函数。由于VS的输出与内核系数是线性关系，故可得其表达式的矩阵形式

x=Z·h+e

(8)

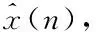
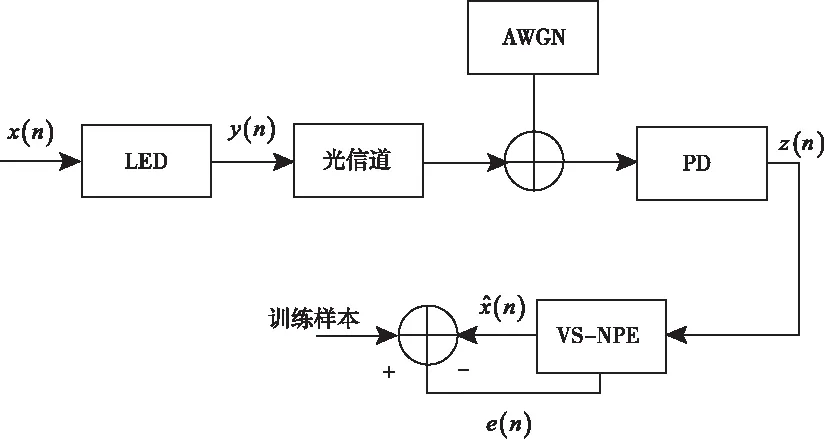
图1 VS-NPE内核参数计算学习框架

2.4 基于SSR-AMP算法的VS-NPE参数计算

CS理论的关键是通过解决以下优化问题来实现重构：

=arg minh‖h‖1s.t.‖Ah-y‖2<ε

(9)

其中，ε是信号重构的上限误差。

AMP[11]算法是解决问题(9)的一种有效方法。该算法从0=0、0=y迭代开始，在迭代t次时，AMP算法可表示为

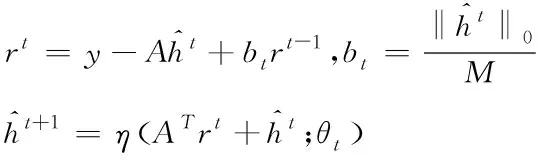
(10)

(10)式中，t∈N是h迭代t次时的当前估计，rt∈M是迭代t次时的残差，而‖t‖0是t的非零数。另外，η(·；·)是软阈值函数，其定义为

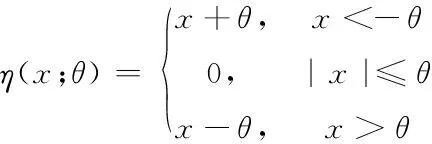
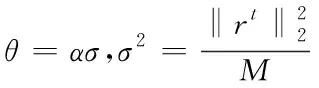
(11)

其中，α是通过迭代固定的调整常数，σ是残差rt的经验度量。

AMP算法有效的前提是观测矩阵应满足i.i.d[13]。由于VS-NPE观测矩阵的列高度相关不满足i.i.d的要求，无法保证AMP算法迭代计算的准确性。因此，提出一种SSR-AMP算法用于VS-NPE内核参数计算，所提算法的原理框图如图2所示。首先归一化处理观测矩阵，然后引入阻尼因子以改进AMP算法的迭代过程，进而追踪稀疏支撑集，最后结合LS计算VS-NPE的内核参数。

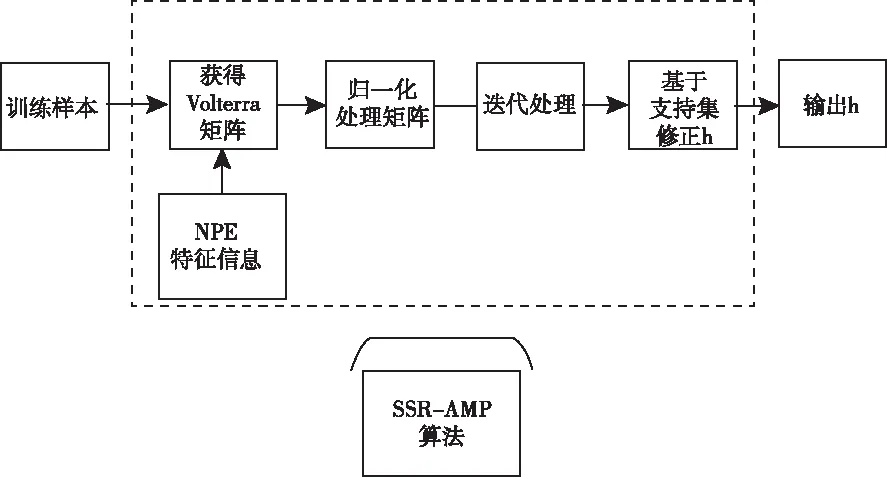
图2 SSR-AMP算法原理框图

根据训练样本的输入信号，基于VS-NPE模型信息生成VS观测矩阵。本文根据观测矩阵的列特征计算归一化因子[12]，先以列向量的形式改写测量矩阵Z

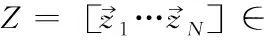
(12)

再以Z中每个列向量的l2范数计算归一化因子

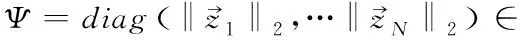
(13)

利用归一化因子将等式(8)重写为

x=ZΨ-1Ψh+e=ZΨhΨ+e

(14)

通过归一化处理Z，使得新矩阵ZΨ克服矩阵Z列高度相关的缺点。

另外，需要注意的是AMP算法迭代计算的准确性在Z归一化处理后仍然无法保证。为了解决这个问题，本文引入阻尼思想[14]，其迭代过程如下

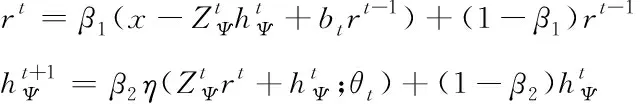
(15)

其中，β1，β2∈(0，1]是阻尼因子，经过多次仿真比较和综合分析后，本文采用β1=β2=0.008。

然后，提取支撑集h=Ψ-1hΨ。其中稀疏支撑集是h的大系数分量的下标集

Ni={i：|(h)i|>μ}

(16)

这里μ是系数阈值。提取Ni后，用LS计算基于Ni的uΨ，其中uΨ=h(Ni)。迭代可得

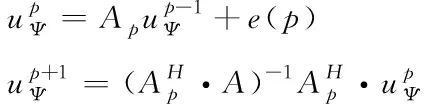
(17)

最后，根据Ni的信息对h进行重构，即得到VS-NPE内核参数。借助阻尼技术，可有效提升AMP算法收敛性、保证局部稳定性，从而降低AMP算法发散的可能性。

3 仿真分析

本文借助Matlab搭建基于DCO-OFDM的VLC系统。仿真中训练样本和测试样本均是长度为62400的DCO-OFDM信号，取VS-NPE非线性阶数k=5、记忆深度D=3，阈值函数中的调整常数α为1.39。

首先对比研究LS、RLS、Kalman滤波[15]、OMP[16]、SSR-AMP等5种算法的VS-NPE内核参数提取性能。以平均归一化均方误差(NMSE，Normalized Mean Square Error)来衡量各个算法计算精度。

无噪情况下，选取25组训练长度Υ=400和Υ=800的训练样本，采用上述5种算法计算VS-NPE内核参数，仿真得到各个算法NMSE对比如图3所示：当Υ取值不同时，各个算法相应的NMSE变化幅度也不同；LS和Kalman滤波的NMSE受训练长度的限制较为明显，波动幅度较大；而RLS、OMP、SSR-AMP等都表现了较好的稳定性；另外，RLS和SSR-AMP的NMSE表现最优，可近似达到-30dB，参数计算精度最高。

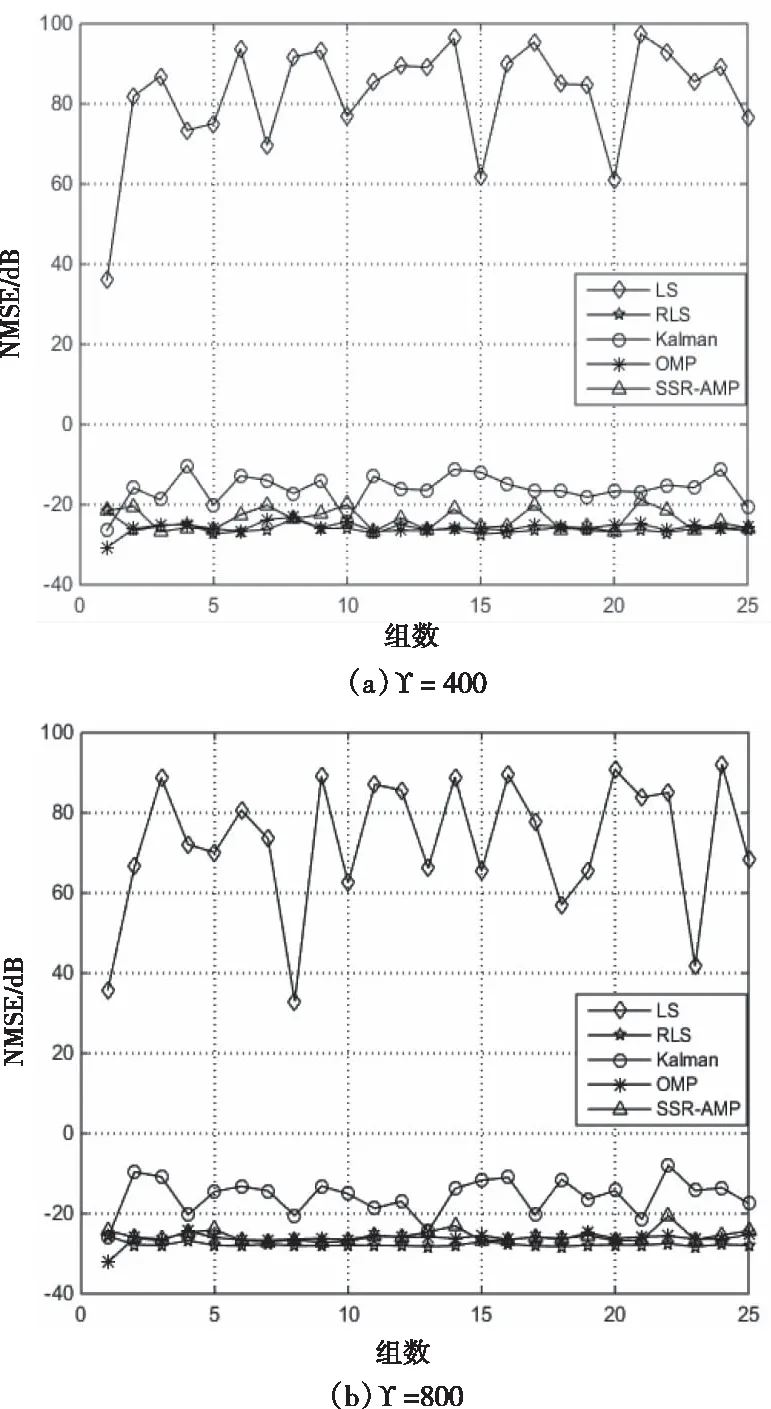
图3 不同训练长度时NMSE结果

另外，实验选取Υ=400和Υ=800时两组NMSE对比结果如表1所示。如前所述，由于VS-NPE观测矩阵列高度相关，因此一定数量的训练样本才能确保基于CS的算法辨识参数正确，这将给信号处理模块带来负担。但是根据表1结果可知，SSR-AMP即使在长度较短的训练样本条件下NMSE也表现出色，以Υ=400为例，其NMSE仍然可达-31.55dB。

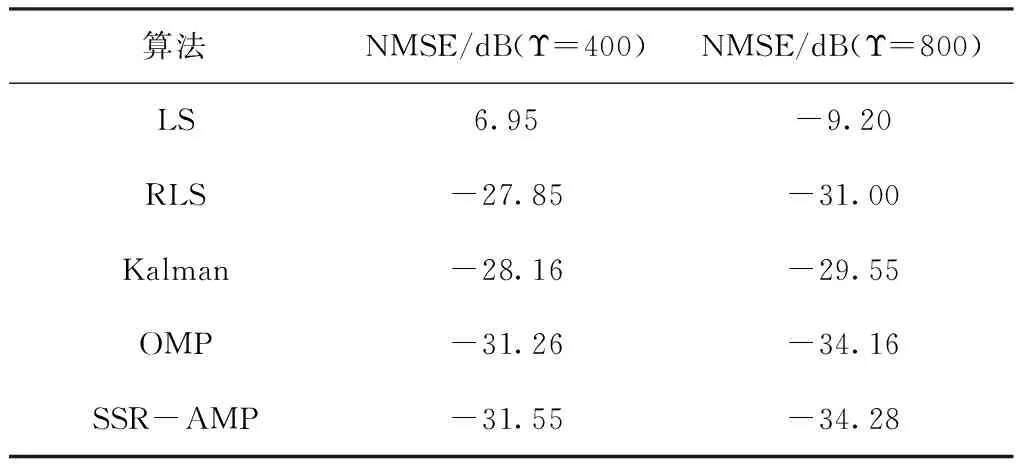
表1 Υ=400和Υ=800时2组NMSE

其次，在Υ=400的条件下对比上述5种算法提取的VS-NPE内核参数数量，对比结果如表2所示：SSR-AMP算法提取VS-NPE内核参数个数最少，比LS、RLS、Kalman滤波和OMP计算所得VS-NPE内核数量分别降低了约83.2%、97.3%、97.3%、27.5%。因此，SSR-AMP算法构架的VS-NPE内核参数少、结构简单，进而可大幅度减少VS-NPE的硬件资源开销。

表2 Υ=400时各算法辨识参数数量

最后，由于缩短训练样本长度可进一步减小训练开销，因此含噪情况下设置Υ=100，对比上述5种算法的NMSE与SNR的变化关系如图4所示：随着SNR的增加，除RLS算法外，其它上述4种算法的NMSE都不同程度的减小，其中SSR-AMP算法的NMSE下降速度显著快于其它4种算法；并且在相同NMSE条件下，SSR-AMP算法更节省SNR需求，以5种算法的NMSE均等于-30dB为例，SSR-AMP的SNR需求比其它4种算法降低约10dB。因此，SSR-AMP算法较其它算法具有更优异的参数提取性能。

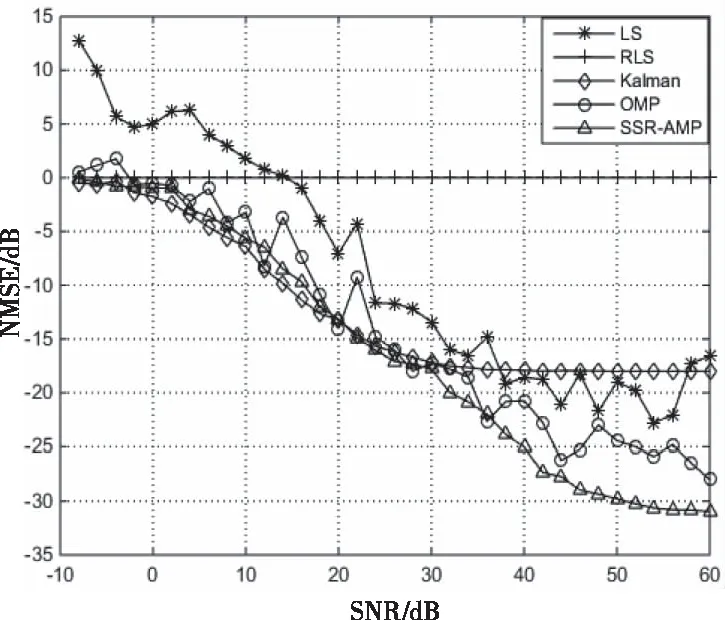
图4 Υ=100时NMSE和SNR关系曲线

4 结论

本文提出一种SSR-AMP算法用于计算VS-NPE内核参数，该算法结合了CS中改进的AMP算法及LS算法，通过有效稀疏支撑集提高VS-NPE内核参数提取准确性。仿真结果表明，相较于传统LS、RLS、Kalman滤波和OMP等算法，SSR-AMP算法具有更高的精确性和稳健性。针对短训练样本的苛刻条件下，SSR-AMP计算所得VS-NPE内核数量最少，同时所得NMSE最小且最稳定，展示了该算法强健的参数提取能力。在后续工作中，需对SSR-AMP算法迭代过程进行优化，从而进一步地降低算法计算复杂度。