集成PSO-NN模型在房价预测中的应用研究

段永辉，高 绅，郭一斌，王 翔

(1. 河南工业大学土木工程学院，河南 郑州 450001；2. 郑州航空工业管理学院土木工程学院，河南 郑州 450015)

1 引言

经过二十多年的快速发展，中国房地产市场已经逐步趋于成熟。高额的住宅价格一直是政府部门和人民群众关注的热点。如何准确预测住宅价格走势和价格波动区间一直是学术界关注的重要的经济课题。准确的预测住宅价格不仅可以为消费者与投资者提供购房意向参考，同时也可以为政府相关部门发布购房政策提供理论依据。因此，探索一套快速高效的商用住宅价格预测模型对房地产市场的健康发展十分重要。

针对商用住宅价格的预测的问题，国内外学者进行了各种各样的尝试，旨在寻求一种快捷高效的预测方法。目前，以自回归移动平均模型(Auto-Regressive and Moving Average Model，ARMA)为代表的传统预测模型虽有强大的数学理论基础支撑，但仍存在准确度相对较低的问题。近年来，速率更快准确度更高的机器学习模型已被多位学者引入住宅价格预测问题的研究中，显示出良好的效果。

在众多住宅价格预测的研究中，文献[1-3]采用线性回归模型进行预测，但是该模型不能进行有效处理非线性数据，同时其重点是解释而非预测，且对类似工程数据样本大小与工程项目相似程度依赖性较大[4]。支持向量机模型(Support Vector Machines，SVM)[5-7]是一种基于结构风险最小化原理的统计学习算法，该算法理论基础扎实，泛化能力强，能够有效处理非线性问题，但是也存在处理大样本数据速度较慢，以及参数及核函数选取对模型预测结果影响较大等问题。文献[8，9]将集成学习模型(Ensemble Learning)应用于住宅价格预测问题的研究中，并取得良好的预测效果，但该模型仍然存在理论框架不统一、集成标准难于确定、训练样本不足、集成算法之间度量差异等问题[10]。

人工神经网络(Artificial Neural Network，ANN)[11]是目前最流行预测算法之一，它对于建模的限制较少，只要拥有足够样本就可以进行预测。目前，针对住宅价格预测问题，已经有很多学者利用ANN进行了一些有益的尝试，且取得优异的预测效果[12-15]。但是ANN模型也存在容易陷入局部极值的缺陷。

综合以上分析，本文针对商用住宅价格预测问题主要进行了以下两项创新工作。

第一，提出了一种基于粒子群优化的神经网络算法(Particle swarm optimization Neural Networks，PSO-NN)，用于克服ANN模型易于陷入局部极值的缺陷。

第二，为了进一步提升PSO-NN算法的泛化性能，本文基于集成学习的bagging思想，提出了一种集成PSO-NN算法。

2 模型概述

2.1 集成学习

集成学习是一种通过集成策略将多个模型的预测结果融合，从而提高预测精度的方法。它对于模型泛化能力提升具有显著的效果，近年来一直是机器学习领域的研究热点。bagging方法(bootstrap aggregation，Bagging)是集成学习中最经典的策略之一。

Bagging集成策略旨在通过集成多个基学习器，进而提升模型的稳定性和准确性，并有效避免过拟合现象的发生。该策略的基本思想是通过bootstrap方法对训练集采取有放回抽样的方式抽取多个子训练集，并分别对子训练集进行训练，得到相对应的基学习器。本文借助Bagging策略建立集成PSO-NN模型，流程如图1所示。

图1 集成PSO-NN模型

在训练完所有基学习器之后，采用softmax函数对基学习器结果进行加权平均，最后输出结果。softmax函数通过归一化方式，使基学习器的权重均为小于1的正数，且所有基学习器的权重之和为1。该函数能凸显出相对重要的基学习器，即对预测精度更高的基学习模型赋予较大的权值。假设共有n个基学习器，第i个基学习器中预测结果与真实值的百分比误差小于10%的比例为mi，则第i个基学习器的权重xi的计算公式如下所示。

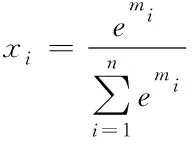
(1)

(2)

2.2 人工神经网络

ANN模型是一种模拟人类大脑信息处理过程的人工智能技术，具有较强的自学习或自组织能力，特别适用于处理非线性现象间的复杂关系。在ANN模型中，信息通过相互连接的神经元进行处理和传递，同时相互连接的神经元分别位于不同的的网络结构层中。典型的网络结构由输入层、隐藏层和输出层构成[16]。

ANN的性能取决于网络结构中各层包含神经元节点的数量。常见的ANN学习过程是学习神经元节点连接的权重，它包含正向传播与反向传播两个步骤，正向传播是输入信息由输入层经隐含层到输出层的过程，若输出层得到的预测结果与真实值之间的误差过大或不满足要求时，则启动反向传播过程，所得的误差信息通过网络从隐藏层传回输入层，进而调节神经元连接的权值与阈值。如此反复的多次训练直至预测结果满足要求为止。目前，较为常用的三层ANN结构如图2所示。

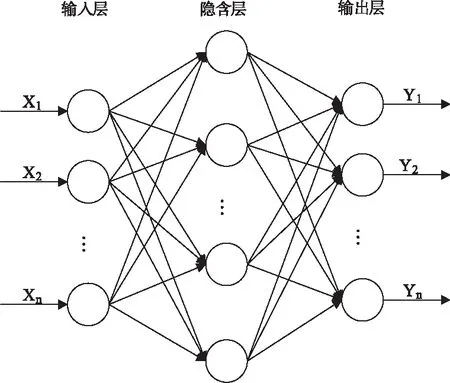
图2 神经网络结构

2.3 粒子群优化算法

1995年提出的粒子群优化算法[17](Particle Swarm Optimization，PSO)是一种基于鸟类捕食行为的进化算法，主要用于求解无约束优化问题。PSO算法是基于种群中个体间的相互合作和信息共享进行寻优求解，它具有操作简洁、参数较少等优点。在PSO算法中，一群粒子代表一个需要优化的个体，每个粒子具有速度和位置两个性质。粒子通过适应度函数衡量当前位置的优劣，进而基于适应度值选择个体的历史最优位置和群体的历史最优位置，最终在连续迭代中找到最优解。标准粒子群算法的数学表达式如下：

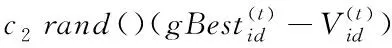
(3)

(4)

其中i=1，2，…，n表示粒子编号；d=1，2，…，D表示问题维度；t表示迭代次数；rand()表示取值为介于0到1的随机数；ω为惯性权重；c1和c2为学习因子。本文设置ω=0.72984，c1=c2=1.496172。pBest为个体历史最佳位置，gBest为群体历史最佳位置，pBest与gBest通过式(5)和式(6)进行更新。在每个粒子进行搜寻时，其移动速度和位置也同样受到搜寻空间的限制，即，V∈[Vmin，Vmax]，X∈[Xmin，Xmax]。

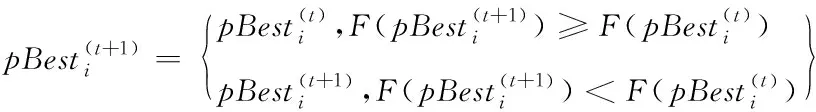
(5)

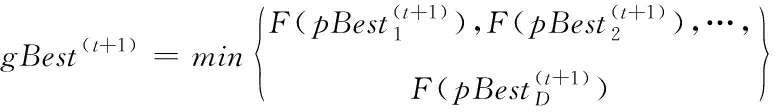
(6)

3 实验准备

3.1 建立指标体系

本文通过整理分析相关文献资料，进而选取了对住宅项目价格具有影响的指标。首先，以“住宅价格特征分析”为关键词在CNKI进行检索，共计得到55篇文献。其次，针对其中29篇核心期刊文献进行重点分析，结果发现土地成本价格是最重要的影响因素之一，由于土地价格受其所在区位影响较大，又考虑到本文仅选取郑州市区内的50组数据进行研究，故本文不对其进行深入研究。最终，将影响住宅特征指标归结为四类：建筑特征、邻里特征、区位特征以及政府调控。针对指标对进一步分析发现，在三篇以上文献中的指标共计18个，占指标总数的80%，需要特别指出的是多位学者对建筑特征类指标进行了重点研究。

基于以上研究，结合专家访谈法和线上咨询法进一步指标筛选，最终确定商用住宅售价影响指标分为以下三类：建筑特征类，邻里特征类和区位特征类，具体包含16个指标，如表1所示。以下所有实验都以郑州市50栋住宅样本的16个指标量化数值作为输入，整个住宅项目的价格作为输出。

表1 商用住宅价格影响因素分析

3.2 评价函数

为了评价不同模型的预测能力强弱，本文选取均方误差(mean-square error，MSE)和平均绝对误差(Mean Absolute Error，MAE)两个最常用的损失函数作为标准。若MSE与MAE值越小，则表明模型预测性能越好；反之模型预测效果越差。MSE和MAE的具体公式如下

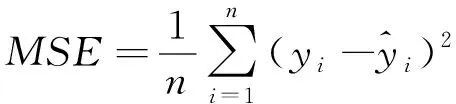
(7)

(8)

3.3 设置对比模型

为检验集成PSO-NN模型预测效果，本文以四类经典机器学习模型针对郑州市50组住宅价格数据进行对比实验。以下是对各模型的简单描述。

集成学习[18]集成学习模型是由多个具有独立决策能力的分类器按照一定的策略组合进行决策分析与预测。根据个体分类器之间的关系，可将集成学习模型分为同质集成和异质集成两类。

线性回归该模型是进行回归分析时一种重要的统计技术，通过建立函数分析多个自变量与因变量之间的线性关系，在小样本情况下效果同样显著。

支持向量机[19]支持向量机模型是以一种监督式学习方法对数据集进行线性分类的分类器。此算法本质上是在三维空间中寻找一个最大边缘超平面(其超平面为二维平面)使得超平面与最近的数据点之间的距离最大。

神经网络模型[11]人工神经网络模型是受生物神经系统启发而建立的智能非参数数学模型。近三十年来，人工神经网络模型在分类、模式识别、回归和预测问题中得到了广泛应用。

4 结果讨论

4.1 单模型预测

对上述给出的集成学习、线性回归、支持向量机和神经网络四类模型分别进行住宅价格预测。为保证实验效果的准确性，在每类模型中分别选出两种常见的子模型进行建模。其中，神经网络模型中ANN模型和PSO-NN模型为三层网络结构，输入层神经元均设置为16个，并通过多次实验对比显示当ANN模型隐含层神经元个数为16、PSO-NN模型隐含层神经元个数为4时两模型预测效果最佳。表2给出了子模型选取以及在三项指标中的预测情况，各模型预测效果如图4所示。

图3 单模型预测结果

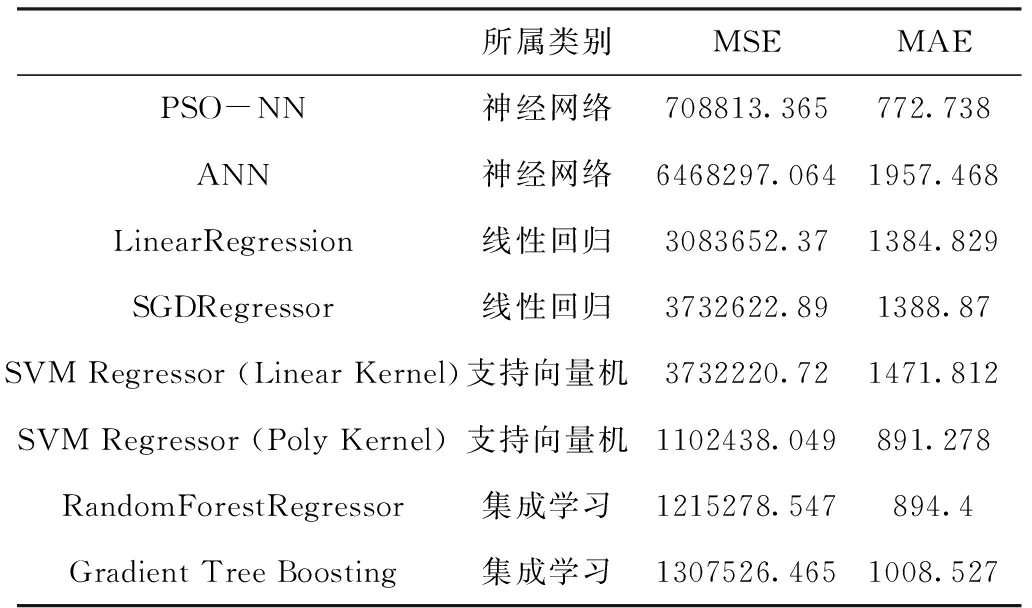
表2 对比模型选取

通过表2和图3可知，四类模型预测中各子模型预测效果各不相同，集成学习模型、支持向量机模型与神经网络模型整体差异不大。为进一步提高对商用住宅价格的预测精度，本文提取四类模型中预测效果更好，且与真实曲线更为贴合的子模型进行进一步分析，分别为集成学习类中的Gradient Tree Boosting模型、线性回归类中的LinearRegression模型、支持向量机类中的SVM Regressor (Poly Kernel)和神经网络类中的PSO-NN模型。

4.2 组合模型预测

在得到四类模型中预测精度较高的子模型后，本文采取以下组合策略进行进一步的预测精度提升：①采取bagging集成策略对PSO-NN模型进行集成优化；②对上述四种表现最好的单模型结果进行算数平均法组合；③采取softmax函数思想对四种单模型进行加权平均法组合。各模型在MSE和MAE评价指标中的预测结果如表3所示。

表3 各模型实验结果对比

通过表3可知，经过组合策略优化的模型精度整体上优于单模型预测，其中集成PSO-NN模型在上述模型中的两项指标排名均为第一，相较于单模型中预测效果最优的PSO-NN模型在两项指标中分别提升了26.14%和27.61%；在组合模型中，集成PSO-NN模型比排名第二的softmax加权平均法预测精度分别提升了35.11%和24.41%。综上所述，经bagging集成策略优化的PSO-NN模型在商用住宅价格预测问题中效果最佳。

4.3 bagging集成效果分析

为清晰展示集成PSO-NN模型对住宅价格预测效果的提升程度，本文对集成PSO-NN模型及其子模型从拟合曲线效果和可信度分析两个角度进行效果对比。

图4为集成PSO-NN模型、PSO-NN模型与ANN模型的预测结果与测试集真实样本的拟合曲线，通过对三条曲线的对比分析，集成PSO-NN模型与真实曲线更为贴合，ANN模型贴合程度最差。

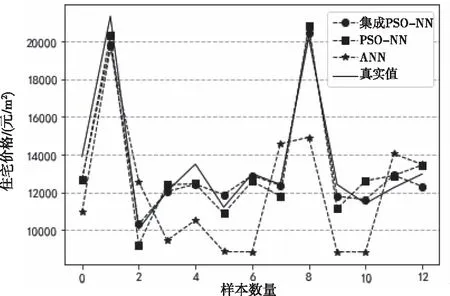
图4 bagging集成策略拟合效果

可信度分析是指通过设置百分比误差来衡量模型预测结果与真实样本之间的差距[20]，并定义当百分比误差在区间[0，10%]时具有较高的可信度，当百分比误差在区间(10%，20%)时模型预测结果可信度为中等，当百分比误差在区间[20%，100%]时结果可信度较低。百分比误差计算公式为

(10)

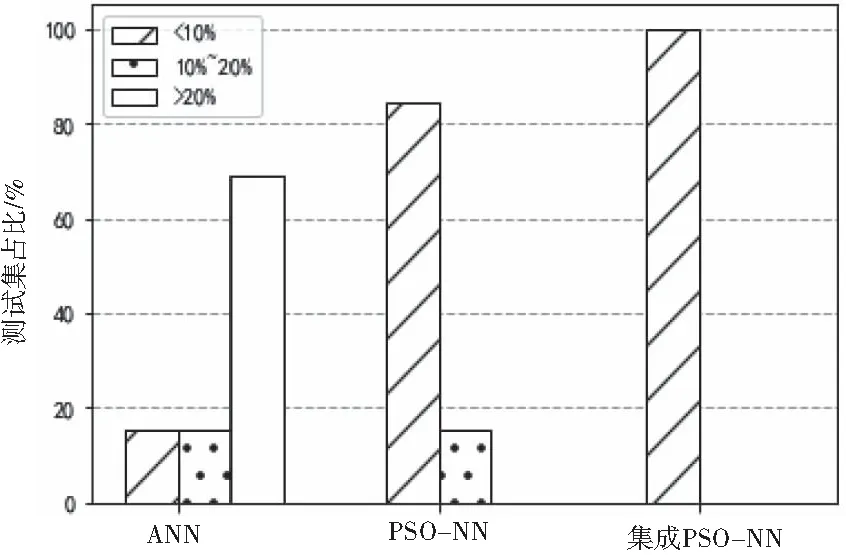
图5 可信度分析

图5为本文三种模型的可信度分析结果，从图中可以看出，集成PSO-NN模型在10%以内的百分比误差相较于PSO-NN模型和ANN模型分别提升了15.38%和84.62%，集成模型的全部预测结果都处于可信度较高的区间范围内，进一步说明该模型在住宅价格预测问题中优势较大。

综上所述，在商用住宅价格预测问题中，对于神经网络模型中收敛速度慢，易陷入局部极值等问题导致的模型预测结果较差，粒子群优化算法具有较好的解决能力，同时使用bagging集成策略对单模型预测精度具有明显的提升效果。

5 结论

本文针对住宅价格预测问题，提出一种基于bagging集成策略的PSO-NN模型，通过对郑州市50组商用住宅项目数据进行仿真，得出以下结论：

1)相对于神经网络模型、集成学习模型、支持向量机模型和线性回归模型这四类传统机器学习模型，集成PSO-NN模型具有较高的预测精度，并在均方误差、平均绝对误差两项指标上相较于最优的单模型算法分别提升了26.14%和27.61%；

2)使用算术平均法和softmax加权平均法组合策略对上述四种单模型进行模型组合，预测结果精度整体上有一定幅度的提升，但预测效果与bagging集成学习策略有一定的差距；

3)集成PSO-NN模型在可信度分析角度相对于PSO-NN模型和ANN模型预测精度分别提升了15.38%和84.62%，且集成模型全部预测结果都处于可信度较高的区间范围，从而反映出本文提出的集成模型在商用住宅价格预测问题中具有较高的实用性。