能耗控制视角下的MOPSO爆破参数优化研究
过 江,赵培东,张 琛,李萍丰,刘 翼,张兵兵
(1.中南大学资源与安全工程学院, 长沙 410083;2.宏大爆破工程集团有限责任公司, 长沙 410083)
爆破手段是现阶段露天矿开采、隧道建设、废弃建筑物拆除等工程作业进行的首选方式,爆破参数的合理设计是爆破作业的重要环节。传统的矿山爆破参数优化方法以理论计算与现场实验相结合为主[1],近年来理论计算、数值模拟、工程实证相结合的研究方式[2-3]因成本较低而受到更多关注,基于大量数据分析的神经网络等智能算法在矿山爆破参数优化[4]和成本控制研究[5]方面也取得显著成果,矿山全作业链生产数据的综合分析运用的重要性愈发突出。国外学者Behrouz等[6]利用随机森林分析了Detour Lake露天矿2013年至2016年的爆破数据,并以铲装和运输环节的载量和效率为爆破效果评价指标优化爆破参数。特别指出的是,生产实际中理想爆破效果的取得是通过在合理范围内调整孔网参数等可调参数的取值来实现的[7-8],而参数的取值存在依赖于生产经验的不足。
粒子群优化算法(PSO)在处理多参数指标寻优方面拥有强大功能。在露天矿山运输路径优化和运输成本控制研究上,粒子群算法因其算法简单和寻优结果精度高、收敛快的特点,有效的实现了露天矿山运输路径优化[9-11],改善露天矿山运营现状。岳中文等[12]提出粒子群算法与支持向量机结合的 PSO-LSSVM 模型,在露天矿爆破振动效应预测方面取得较好结果。目前,多目标粒子群优化理论和应用研究取得丰富成果,MOPSO 算法的核心内容包括非劣解集中粒子的密度信息估计、Pareto 最优解搜索算法和解的多样性保持技术[13]。
在矿山的相关研究和生产实践中,越来越多的学者意识到着眼于矿山生产全作业链,将钻爆、铲运、破碎作为整体来研究矿山效益优化问题是必要和重要的[14-15],且普遍认为钻爆环节直接影响爆破效果,进而影响着铲运、破碎过程的效率、能耗及综合成本[16-18]。但由于爆破机理复杂,影响因素与指标之间往往是非线性关系,很少有研究直接将爆破参数与铲运及破碎指标建立联系。因此,将爆破设计参数作为输入量,选取作业链上某一环节的关键指标作为输出量进行研究,对露天矿山降本增效和能耗控制具有十分重要的意义。
在能耗控制和节能减排标准日益严格的背景下,基于上述现状,提出一种爆破参数优化和爆破效果评价新思路,即建立爆破可调参数与粗碎、中碎及细碎3个骨料加工破碎阶段能耗指标的MOPSO模型,并将能耗指标作为爆破效果的评价指标,结合修正Kuz-Ram模型,通过理论计算和对比分析佐证了寻优结果的正确性。
1 基本原理
1.1 MOPSO基本原理
粒子群优化算法属于智能群体算法(SI),即来源于对自然界中昆虫群体的观察和模拟,粒子群优化算法是对鸟群觅食的模仿。基本原理是粒子根据自身最优位置和全局已知最优位置来动态调整下一步运动速度和位置,被优化函数即适应度函数决定着粒子的适应值。实现动态调整的核心是速度更新公式和位置更新公式。MOPSO的发展基于常规粒子群优化算法(PSO),搜索时只考虑粒子速度和位置的变化,由Coello[19]等人提出。
多目标粒子群算法(MOPSO)具有检索高效、帕累托前沿分布良好的优点,被广泛用来优化工程实际中的数学问题。与常规粒子群算法(PSO)不同,多目标粒子群优化(MOPSO)的一组解由帕累托前端作为标准来衡量该组解中每个解的独特优势,且MOPSO能迅速收敛到帕累托前沿[20]。速度和位置更新公式见式(1)、式(2)。
(1)
(2)
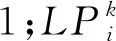
1.2 爆堆块度预测基本原理
多目标粒子群优化算法求解得到相对最优解集的帕累托前端和对应参数取值。结合砂石矿山爆破实际,对爆破块度预测理论Kuz-Ram模型加以修正,验证寻优结果的正确性和以能耗指标作为爆破效果评价指标的合理性。
Kuz-Ram模型是由研究爆破平均块度的库兹涅佐夫(Kuznestov)模型和研究块度分布特征的罗森雷姆勒(Rosin-Rammler)模型结合而来,并利用Rosin-Rammler模型曲线把Kuz方程变成预报爆堆级配的数学模型。鉴于工程实例选取的是砂石骨料露天矿山,爆破参数设计时需考虑爆后最大矿石块度的限制,故参考文献[17]引入矿块允许最大块度Xm这一参数,对Kuz方程进行修正,见式(3)。
(3)
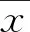
Rosin-Rammler曲线用于描述被爆岩石破碎情况[21]:
(4)
式中:R为筛上矿石占比,即块度大于x的矿石所占的比率;x为筛孔尺寸,表示筛下最大块度或筛上最小块度;xe为特特征尺寸,由Kuz方程计算给出;β为均匀度指标,经验系数,取0.8~2.2,值越高表示爆堆块度越均匀,值偏低归因于粉矿和大块率占比较大,计算公式见式(5)。
(5)
式中:W为最小抵抗线;φ为炮孔直径;ΔW为凿岩精度的标准误差,即孔底偏离设计位置的平均距离;A为孔距与最小抵抗线之比;L为底板标高以上药包长度;H为台阶高度。
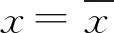
(6)
2 基于数据离散化处理的MOPSO模型建立
通过数据预处理和参数数据离散化处理,并运用回归分析建立能耗指标适用度函数代理模型,利用MATLAB软件运行MOPSO算法进行寻优,最后以修正的Kuz-Ram模型计算优化参数的爆堆块度理论值,佐证寻优参数的合理性和以研磨破碎环节的能耗指标作为爆破效果评价指标的适用性。
基于数据离散化处理的能耗指标与爆破参数MOPSO模型建立步骤如下:①现场数据收集并数据预处理;②可调参数数据离散化处理;③回归分析建立能耗指标与可调参数的代理模型;④初始化粒子群;⑤迭代更新粒子的速度和位置及更新储存库,产生新一代粒子群和新的全局和局部最优位置;⑥最大迭代次数为Maxlt时结束迭代,得出帕累托最优前沿和其他解;⑦借助MATLAB提取帕累托前沿上的多个最优解;⑧选择3组具有代表性的解,用修正Kuz-Ram模型佐证优化结果的合理性。
3 能耗指标与爆破参数MOPSO模型的运用与分析
3.1 数据处理及指标选取
大皇山凝灰岩矿开采爆破采用中深孔爆破技术,运用数码电子雷管实现逐孔延时起爆。砂石骨料加工经过3个阶段的破碎,即粗碎、中碎、细碎,共配置有17台破碎机,是主要耗电设备。其中粗碎和中碎过后经一道筛分将块度大于31.5 mm的矿石输送经由细碎阶段进一步破碎为31.5 mm以下的骨料。
原始数据来源于大皇山凝灰岩露天矿生产现场统计,选取的数据有研磨破碎3个阶段能耗数据和3个可调参数(孔排距、钻孔超深、炸药单耗)数据。由于每日生产计划不同,需要破碎的进矿量也就不同。为减小破碎量不同造成的能耗差异,选取耗量比HL(kwh/m3)作为回归分析指标,反映破碎1 m3进矿量需要消耗的电量。经异常数据剔除后,现场统计的完整数据有25组。经分析发现如下规律:
1)孔排距与能耗指标呈现正相关关系,孔排距越大,耗量比越大;
2)炸药单耗与能耗指标呈现负相关关系,炸药单耗越大,耗量比越小;
3)钻孔超深与能耗指标呈现负相关关系,钻孔超深越大,耗量比越小;这与超深增加,在填塞长度不变的情况下,实际炸药量增加有关;
4)细碎阶段的能耗受骨料产品生产尺寸要求影响更大,与粗碎和中碎的耗量比成负相关。
以上规律与爆破参数对爆破块度的影响规律[6]相似,说明以研磨破碎环节的能耗作为评价爆破效果的间接指标有一定的适用性。
根据生产实际,可调参数调整范围不大,将统计到的参数数据离散化为4组,并对应赋予1到4的整数指针编码。特别的,将孔排距整体作为一个参数,选取6.2 m×3.0 m、6.2 m×3.2 m、6.5 m×3.2 m、6.5 m×3.3 m 4组数据。本研究目的之一是在现有的爆破可调参数范围内寻优,回归分析建立的代理模型能否最佳拟合现有参数与能耗指标是关键。故选取MATLAB散点图中相关关系最好的7组数据用于建立代理模型。指标数据及指针编码如表1所示。
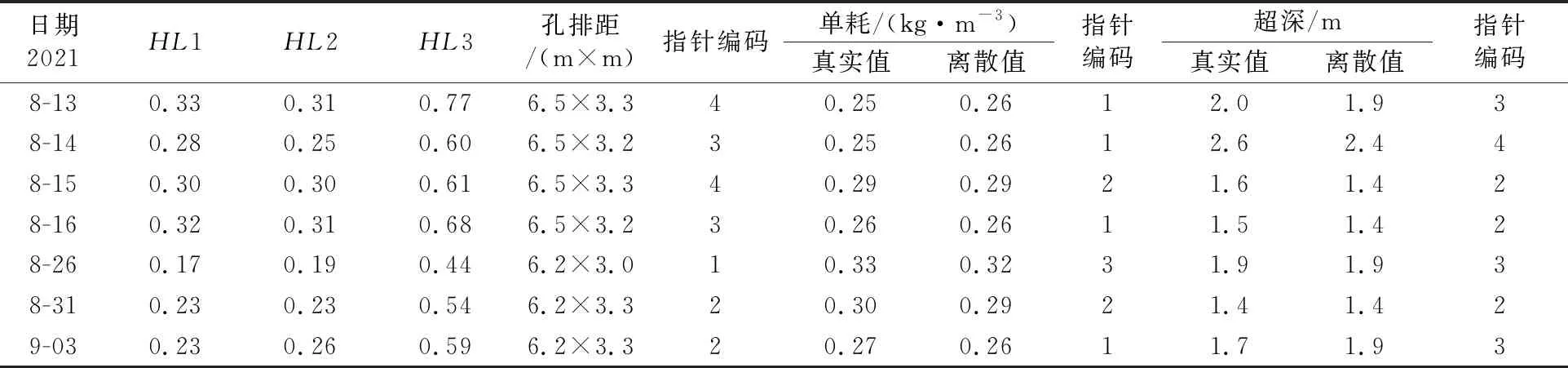
表1 指标数据及指针编码
3.2 能耗指标代理模型建立
在多参数与指标,即自变量与因变量之间的函数关系不明确的情况下,其函数关系用多项式函数模型表示为Y=f(x1+x2+x3)+ε,即
y=b0+b1x1+b2x2+b3x3+…(线性项)
b12x1x2+b13x1x3+b23x2x3+…(交互项)
(7)
b11x12+b22x22+b33x32+…(二次项)
ε~N(0,σ2)
根据参数现实意义,孔排距、炸药单耗、超深3个参数的两两组合没有对应的量纲,故回归分析不考虑含交互项的代理模型。建立线性代理模型和非线性代理模型(含线性项)即纯二次模型,并通过比较线性模型和非线性模型的相关系数和显著水平来确定代理模型的最佳形式。一般认为,判定系数越大,即越接近1,显著水平P越小,回归分析建立的模型越符合原始数据趋势。设孔排距为x1,炸药单耗为x2,钻孔超深为x3,粗碎耗量比为HL1(x1,x2,x3),中碎耗量比为HL2(x1,x2,x3),细碎耗量比为HL3(x1,x2,x3),回归分析得到的系数、判定系数r2、显著水平概率p如表2所示。

表2 回归分析建立模型的相关参数
在显著水平为 0.05 时,表2线性代理模型和纯二次代理模型反映能耗控制指标与影响因素之间关系。从对应的判定系数、概率值p的比较来看,纯二次模型的p值均不理想,尤其是细碎耗量比的代理模型p值最差,这主要是数据点不足导致的纯二次回归分析显著性不高;而纯二次代理模型的判定系数均大于0.95,说明对已知数据点的拟合效果很好,与原始数据的反映规律相关性更高,这也与爆破各因素之间关系呈现非线性的实际情况相符。线性代理模型显著水平均小于0.05,判定系数均大于0.92。从显著性和相关性判断出线性模型更能拟合当前已知数据,作为适应度函数在MOPSO算法中的寻优结果更为准确。因此,对现有数据来说,线性模型优于纯二次模型,故反映能耗控制指标与影响因素之间关系的代理模型为线性模型,即
HL1(x1,x2,x3)=0.194 3+0.041 3x1-0.020 9x2-0.001 8x3
(8)
HL2(x1,x2,x3)=0.265 3+0.026 4x1-0.026 0x2-0.010 3x3
(9)
HL3(x1,x2,x3)=0.560 5+0.052 4x1-0.076 4x2+0.012 0x3
(10)
3.3 能耗指标与爆破参数MOPSO寻优结果与分析
根据3.1的分析规律,粗碎耗量比和中碎耗量比与细碎耗量比呈负相关,故建立两个适应度函数和三个适应度函数的MOPSO寻优模型,表达式见式(11)。
Min{[HL1(x),HL3(x)],[HL2(x),HL3(x)],[HL1(x),HL2(x),HL3(x)]}
X=[x1,x2,x3]T1≤x1≤4,1≤x2≤4,1≤x3≤4
(11)
基于MATLAB R2019(b)仿真软件运行能耗指标与爆破参数MOPSO模型,并求解式(11)中3类组合的帕累托前端。
2目标组合和3目标组合寻优的帕累托前端如图1、图2和图3所示。
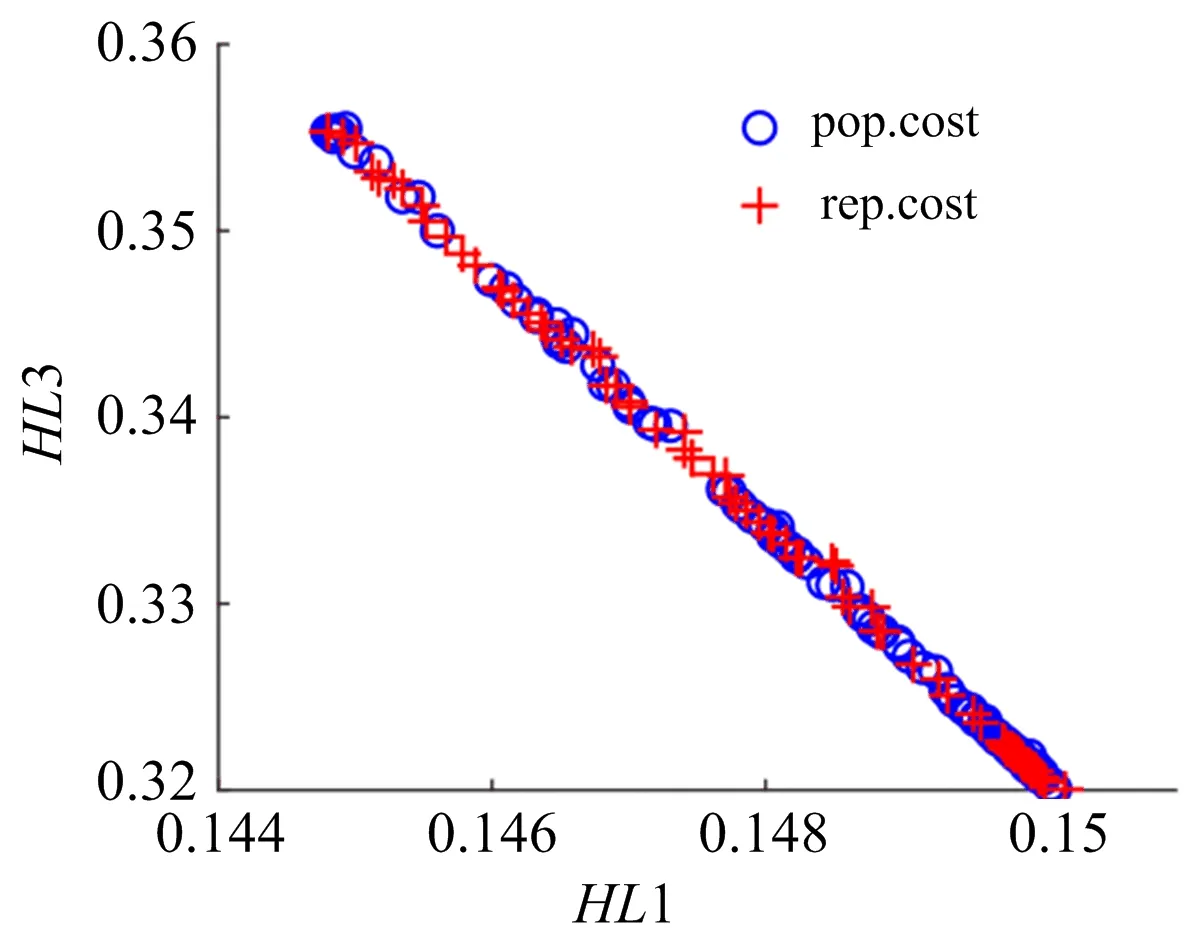
图1 粗碎与细碎耗量比两目标帕累托前端
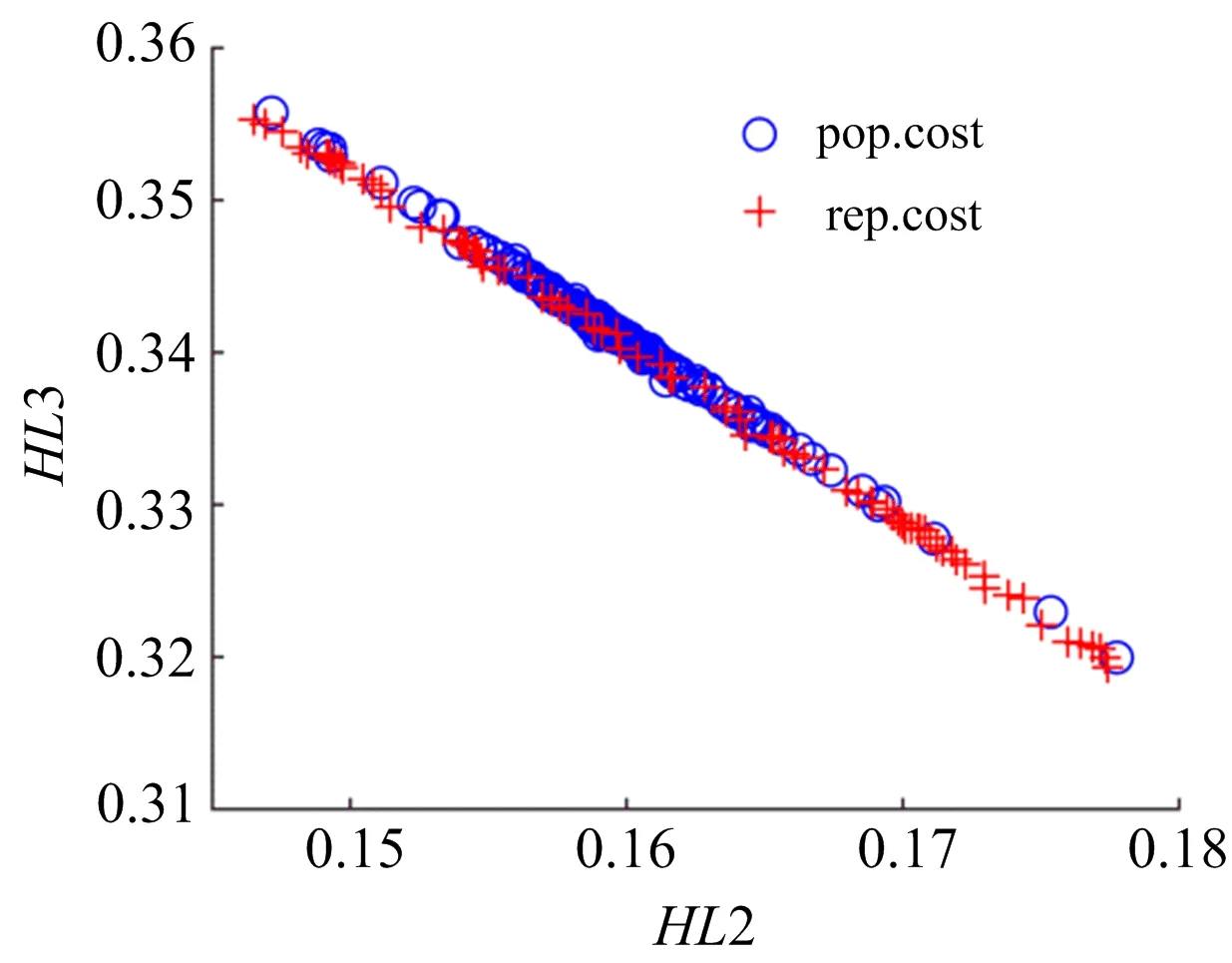
图2 中碎与细碎耗量比两目标帕累托前端
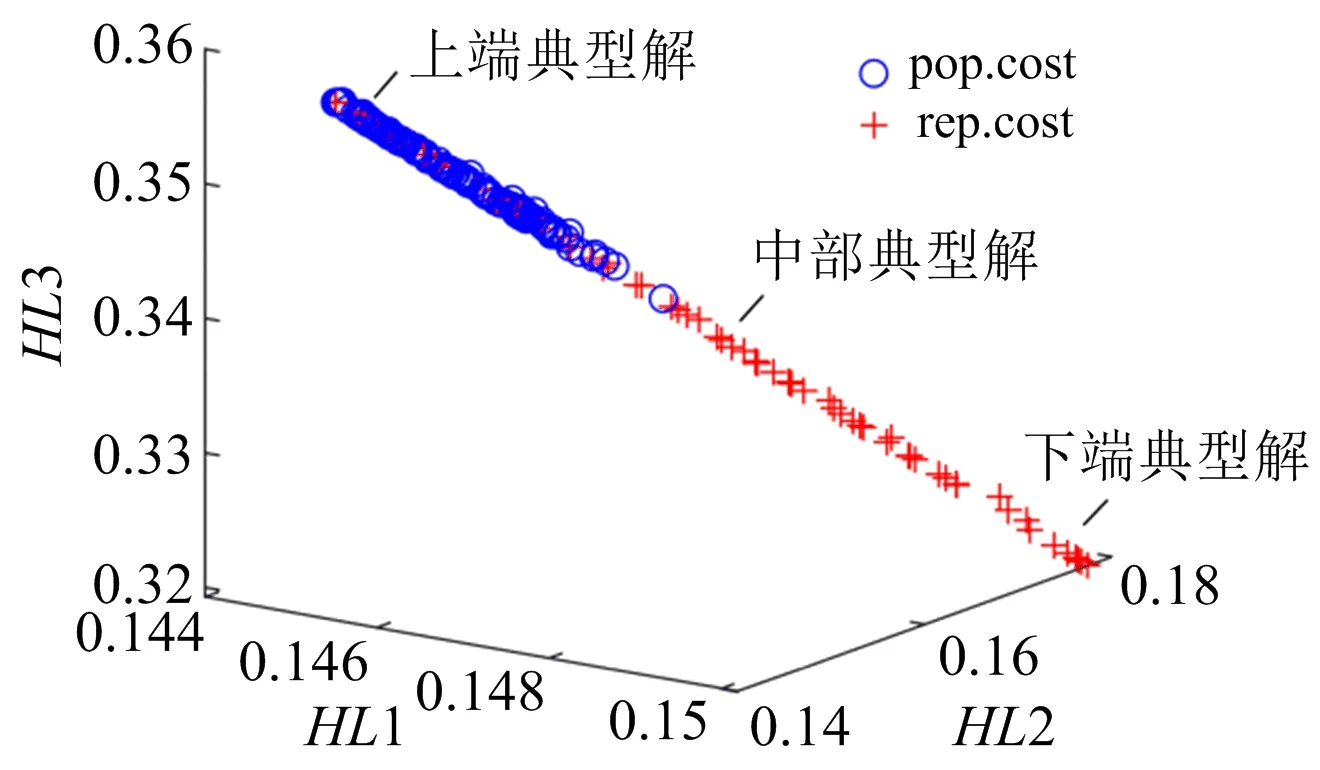
图3 三目标帕累托前端
当迭代次数为200时,图1、图2、图3为耗量比代理模型寻优得到的帕累托前端,图中显示最优解集分布均匀,表明研磨破碎三阶段的耗量比代理模型在MOPSO算法中获得准确的寻优结果。
多目标粒子群优化算法得到的解是1组相对最优解,2目标适应度函数和3目标适应度函数并非同时获得最优解,即通过帕累托最优前沿来确定每个解相对其他解所具有的独特优势。故选取帕累托前沿曲线或曲面的上端、中部、下端3组典型解来代表帕累托最优,不用全部提取帕累托最优解来分析研究便满足研究需要。最优解提取如表3所示。
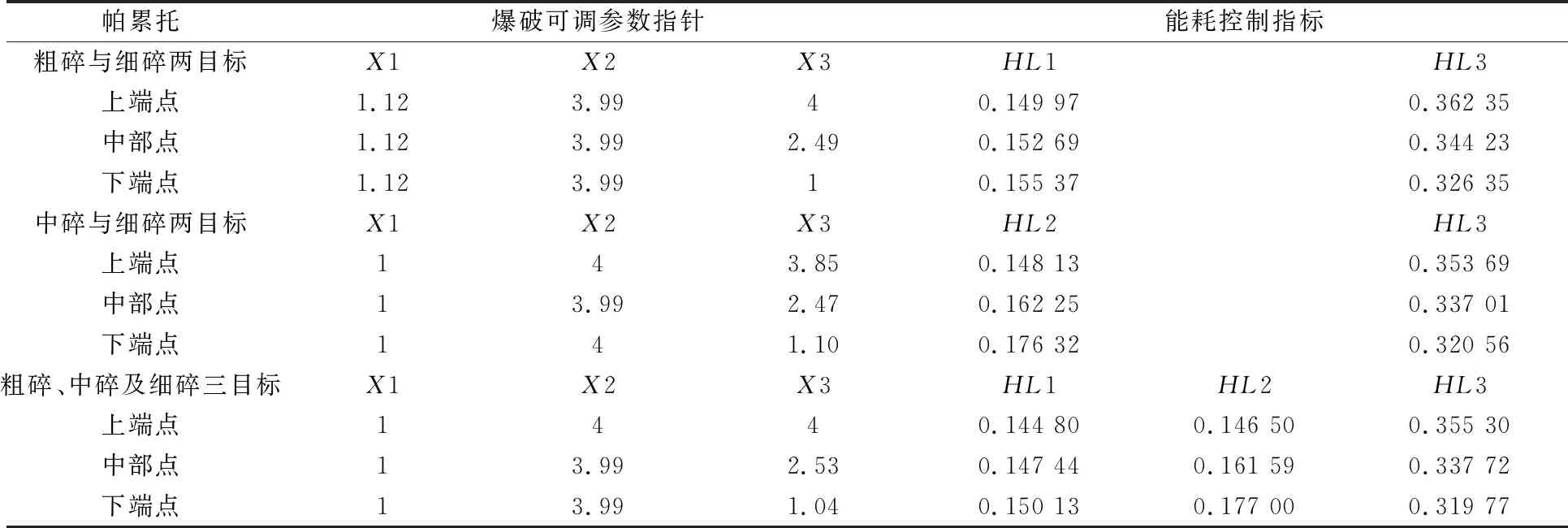
表3 3组典型解提取
从2目标、3目标帕累托前沿分布和3组典型解提取分析可知:
1)在现有爆破参数选择范围内,粗碎耗量比指标取值范围在0.148~0.155 37 kwh/m3,中碎耗量比指标取值范围在0.146 5~0.177 kwh/m3,细碎耗量比取值范围在0.319 77~0.362 35 kwh/m3。
2)研磨破碎三阶段中,细碎耗量比指标最大,破碎1 m3的进矿,HL3超过HL1和HL2约50%;可见保证前两阶段破碎的高效进行,对控制细碎阶段能耗有重要影响。
3)2目标和3目标优化的帕累托前沿分布均说明孔排距越小、炸药单耗越大,研磨破损三阶段的耗量比就越小。
4)在相对最优耗量指标范围内,超深越大,粗碎和中碎耗量比越小,细碎耗量比越大。即在合适的填塞长度下,增加超深使得底部岩石破碎程度增加[22],从而岩石整体平均破碎程度更佳。最终粗碎和中碎的耗量比变小,矿块破碎效率变得更高,破碎环节整体能耗减少。
由MOPSO算法帕累托前端结果可知,在相对最优的能耗控制指标下,孔排距和炸药单耗参数指针分布为1和4,对应参数真实值孔排距为6.0 m×3.0 m,炸药单耗为0.35 kg/m3。从研磨效率提高的角度看,超深在合理范围内取值应偏大,在1.7~2.0 m之间。
3.4 Kuz-Ram模型验证优化结果
大皇山凝灰岩矿采区内岩层主要为凝灰岩类岩石,岩石节理、裂隙不发育。属于坚硬岩石类,故岩石计算系数K取13。为达到预期的爆破效果选用爆速较高的乳化炸药药卷直径d=115 mm。硝铵乳化炸药不含梯恩梯成分,对环境友好。炸药相对威力E取值100。石料允许最大块度取值0.8 m。修正的Kuz-Ram模型中,孔距与最小抵抗线比值A、单孔装药量Q、单孔破碎岩石体积V03个参数因孔排距和炸药单耗不同而取值不同,其他参数取值如表4所示。

表4 Kuz-Ram模型参数取值
由3.3MOPSO优化结果可知,孔排距取6.0 m×3.0 m,炸药单耗取0.35 kg/m3,利用式(1)至式(4)修正的砂石露天矿Kuz-Ram模型对优化结果进行理论上的对比验证。参数优化结果与表1中爆堆平均块度和块度特征尺寸的比较如图4所示,爆堆级配即筛上各块度矿石占比的对比数据如图5所示。
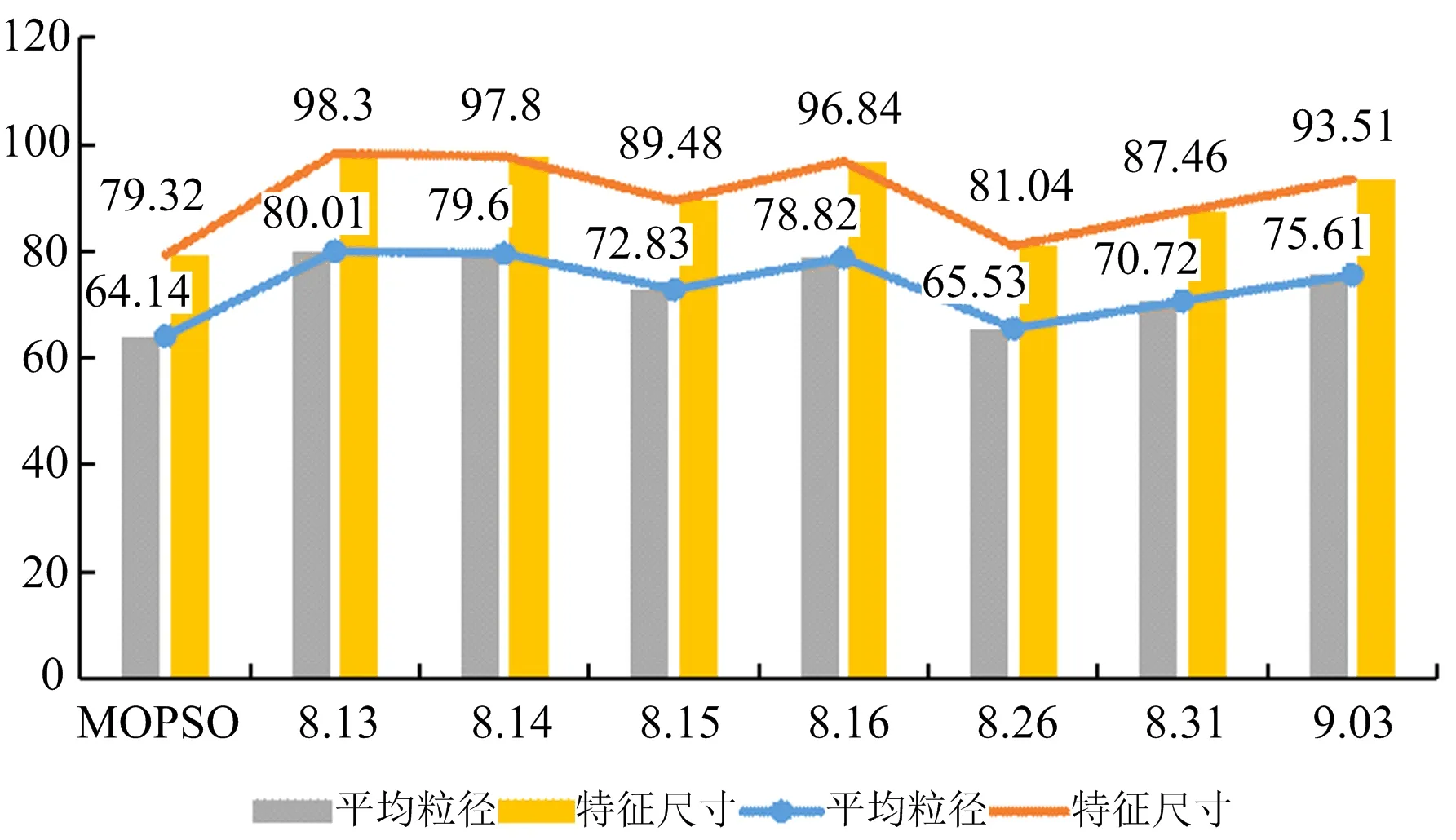
图4 爆堆平均块度和特征尺寸的比较
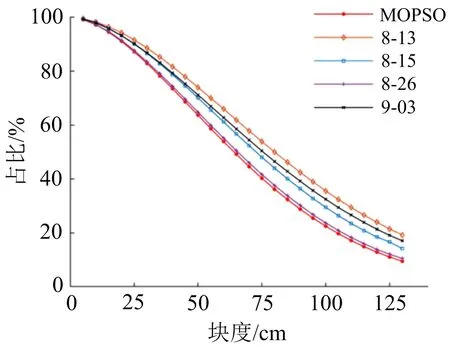
图5 筛上各块度矿石占比R值描点对比
从平均块度和特征尺寸对比结果分析来看:
1)MOPSO算法寻优在满足耗量比能耗指标相对最优的情况下搜寻到参数值对应的爆堆平均块度小于未经优化的参数对应的值,表明该参数在实际爆破中将取得较为良好的岩石破碎效果,块度分布更为均匀。
2)优化结果对应的筛上矿石占比曲线下降速率快于其他4组数据对应的曲线,表明爆堆级配优于未经优化的4组参数对应的爆堆级配;当块度为130 mm时,优化结果对应筛上矿石占比为9.5%,小于其他4组数据对应的值,表明优化参数将取得较小的大块率。
综上,以多目标粒子群寻优得到的爆破可调参数经理论计算和比较能够取得良好的爆破效果,也说明以研磨破碎阶段的能耗控制指标耗量比为爆破效果的间距评价指标是可行的。
4 结论
1)建立研磨破碎能耗指标与爆破可调参数的优化模型,并以耗量比适应度函数两目标和三目标组合的方式,运用MOPSO算法对爆破可调参数进行寻优,得到可调参数的最优组合为孔排距取6.0 m×3.0 m,炸药单耗取0.35 kg/m3,超深根据实际情况在1.7 ~2.0 m之间取值;同时还得到研磨破碎的细碎阶段是主要耗能环节,耗能指标超粗碎和中碎50%,超深的合理取值能够提高研磨破碎环节的效率。寻优结果为爆破参数的合理选择和露天矿山破碎能耗控制提供了理论支撑,减少对人工经验的依赖。
2)运用修正Kuz-Ram模型对MOPSO算法寻优参数与未经优化参数理论上的对应爆堆块度进行分析比较,得出优化后的爆破参数对应的平均块度为64 cm,筛上130 cm块度矿石占比为9.5%,均小于未经优化参数对应的值;为破碎能耗指标作为露天矿山爆破效果的评价指标提供理论依据,即较低的耗量比指标能够说明爆破效果比较好;研磨破碎能耗指标作为爆破效果评价指标相较于其他爆破效果评价指标更有利矿山的降本增效和节能减排。
3)受露天矿山现场数据收集涉及的影响因素较多的限制,以及能耗指标与爆破参数的寻优研究对现场各工种及整体施工组织和调度有较高要求,加之人工数据统计存在的不足,本次收集到的实际工程数据主要用于现有参数指标寻优。此外,影响研磨破碎能耗的因素众多,爆破参数作为始端输入因素与其他环节可能存在的影响因素之间的主次关系还有待进一步研究。对爆破参数与能耗指标的进一步预测还有待更多数据样本的获取和指标模型的进一步完善。

