双线冻结隧道下穿车站冻胀特性模型试验与工程实测
王延廷,王 磊,李方政,刘志强
(1.中国矿业大学(北京),北京 100083;2.煤炭科学研究总院,北京 100013;3.北京中煤矿山工程有限公司,北京 100013;4.中国铁路工程集团有限公司,北京 100055)
人工冻结法是矿井建设中的一种特殊施工方法,主要应用于矿山井筒施工。1997年,冻结法成功应用于中国市政工程,并在含水软弱地层地下工程建设中得到了广泛应用,解决了许多其他工法难以解决的工程难题[1]。近年来,中国轨道交通大规模建设,新建地铁隧道下穿地面建筑、区间隧道等工程数量逐年增加,城市地表建筑密集的地区,不同轨道交通线路、地下结构之间的隧道穿越工程逐年增多。冻结法作为富水地层新建隧道下穿既有结构施工的重要方法[2–3],具有隔水性好、施工灵活、无需降水等诸多优势,但冻结过程中会产生冻胀现象,是冻结工法的最大弱点。富水地层含水量大、水分补给充沛,人工冻结产生的冻土体量大、冻结速度快,冻胀应力容易引发上覆地表和相邻建筑物出现不均匀变形,造成上覆结构损坏,如图1所示。
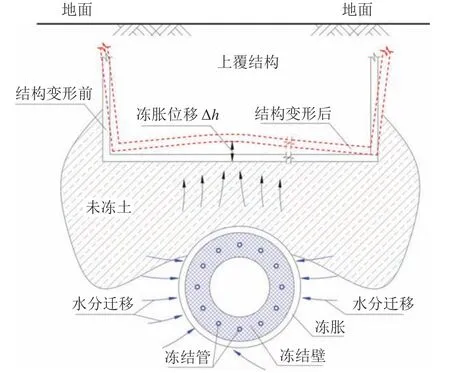
图1 冻结隧道下穿上覆结构冻胀作用示意图Fig.1 Schematic diagram of frost heaving effect of freezing tunnel under and overlying station
为保证冻结隧道下穿上覆结构施工安全,有必要对上部结构在冻结下穿过程中的变形规律进行研究,对冻胀作用下的上覆结构变形进行定量估算,避免结构出现冻胀破坏。人工冻结法最早应用于国外隧道下穿工程建设。1991年,维也纳地铁3号线区间隧道下穿大厦,隧道顶部距离大厦结构底板2 m,Hinkel[4]监测结构不同位置的冻胀量为1~2 mm,开挖后上部结构沉降量为7~9 mm。2002年,德国Fürth市新建双线隧道冻结法下穿历史建筑,隧道顶部距离结构底板5 m,施工过程中上部结构最大冻胀量为20 mm,开挖完成后最大沉降量为10 mm[5]。2005年,奥地利维也纳地铁6号线双线隧道冻结下穿电信大楼,隧道顶部距离结构底板1.6 m,Semprich[6]监测得出大楼底板最大冻胀量为13 mm,开挖后冻胀量降低为3.0~8.5 mm。山田正男[7]基于某冻结工程,计算土体冻结引起的地表位移,得出地表位移计算的经验公式。
国内在冻胀抬升方面研究多聚焦于冻胀引起的地表隆起。蔡海兵等[8]基于随机介质理论建立隧道冻结施工引起地表冻胀位移的历时预测模型,得出了双线隧道采用依次冻结方式可在一定程度上减小地层冻胀位移等结论。阳军生[9]、陶德敬[10]等基于随机介质理论对冻结法施工引起的地表冻胀进行研究,取得了大量有意义的结论。但这些研究的对象是地表变形,无法将地表变形预测公式应用于冻结下穿结构变形计算。上海明珠线二期上体场站区间隧道穿越地铁1号线上体馆站工程是中国冻结法下穿上部构筑物的经典案例,李方政[11]基于该工程得出冻胀与结构相互作用的位移及接触压力,并采用实测数据进行验证。2014年,无锡地铁某区间隧道水平冻结下穿某商场,隧道顶部距离商场基础底板3.7 m,施工完成后商场基础底板沉降2.6 mm[12]。2017年,深圳轨道交通7号线某区间隧道冻结下穿两层建筑及人行道工程[13],施工监测最大冻胀量为5.5 mm。2021年,南京市地铁7号线下穿既有10号线中胜站采用MJS+人工冻结法加固,隧道交叠区结构净距0.6 m,赵宇辉等[14]对MJS加固后的冻结土体温度场进行数值模拟研究。常州地铁1号线某区间隧道冻结下穿常州火车站基础底板,隧道顶部距基础底板3.75 m,马俊等[15]使用冻结壁外围卸水措施对冻胀抬升进行控制。
以上工程可为冻结隧道下穿上覆结构研究提供参考,但相关研究侧重于冻结温度场变化规律及工程效果评价,对冻土与结构在不同工况下的相互作用规律的研究较少,难以为其他冻结下穿工程设计施工提供参考。
上海轨道交通18号线新建隧道穿越地铁10号线国权路车站工程是上海地铁建设中的特级风险工程,拟建隧道处于富水软土地层,采用冻结+矿山法开挖,开挖荒径顶部距离车站底板1.4 m,隧道冻胀对上覆车站影响较大,施工风险极高。为保证隧道冻结下穿上覆车站的施工安全,本文基于该工况进行模型试验和工程实测研究,对比不同施工方案引发上覆结构的变形规律,为冻结下穿工程提供设计参考。
1 工程概况
上海轨道交通新建18号线双线隧道下穿运营地铁10号线车站,暗挖隧道与10号线车站竖直方向斜交,隧道长度为42.0 m,直径为7.7 m,隧道中心线埋深22.2 m。冻结地层位于第⑤11灰色黏土层位,土体含水丰富,承载力低,土体性质见表1。

表1 冻结土体参数Tab.1 Frozen soil parameters
工程设计冻结壁厚2 m,积极冻结期为45 d,在隧道内部设计“十”字型冻结壁作为开挖支撑,上下行线隧道根据施工条件划分为Ⅰ、Ⅱ两个区段。隧道与车站位置如图2所示。
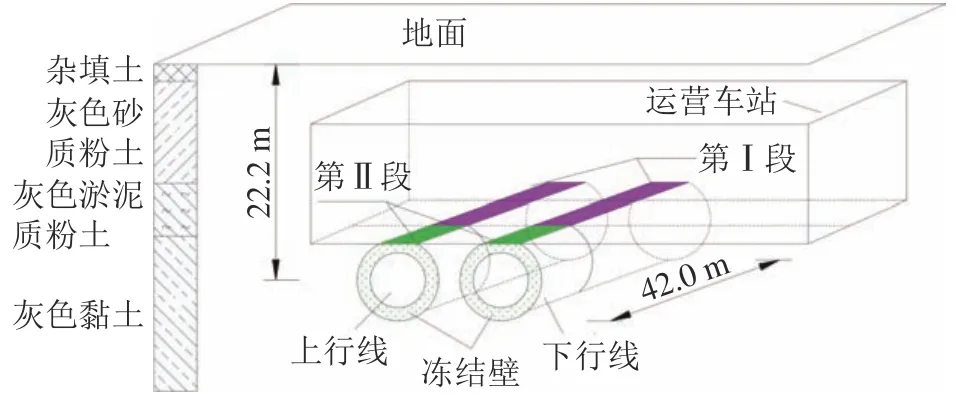
图2 隧道与车站位置示意图Fig.2 Schematic diagram of the tunnel and station location
由图2可知,冻土与车站底板近距离接触,不同冻结模式将对车站底板造成不同的冻胀变形。冻结盐水温度变化、取土卸压、冻结三角区卸压等冻胀控制措施也会对上部车站底板变形产生影响。为研究不同冻结模式引发上覆车站底板变形规律,根据设计方案提出以下两种冻结模式:
1)全长冻结模式,全长冻结即同时开启冻结的长度为上下行线全长(图2中第Ⅰ段+第Ⅱ段),同时冻结上下行线的第Ⅰ段和第Ⅱ段,全长冻结45 d后冻结壁到达设计厚度。全长冻结工序简单,可在短时间内形成稳固冻结壁,工期短;但单位时间所需冷量大,对冻结设备要求高。
2)分段冻结模式,即将上下行线基于Ⅰ、Ⅱ区段进行错时冻结。考虑实际施工过程中积极冻结时间和开挖工序衔接,将不同施工段错开冻结时间设定为30 d。分段冻结方案可以减小单位时间供冷量,有利于工期组织和设备安排;但工期较长,分段冻结及开挖工序如图3所示。首先,开始冻结上行线第Ⅰ段;错时30 d后,开始冻结上行线第Ⅱ段;45 d后,上行线第Ⅰ段到达设计冻结壁厚度,进行开挖;60 d后,开始冻结下行线第Ⅰ段;75 d后,上行线第Ⅱ段到达设计冻结壁厚度,进行开挖;90 d后,开始冻结下行线第Ⅱ段;105 d后,下行线第Ⅰ段冻结壁到达设计厚度,进行开挖;135 d后,下行线第Ⅱ段到达冻结壁设计厚度并开挖。
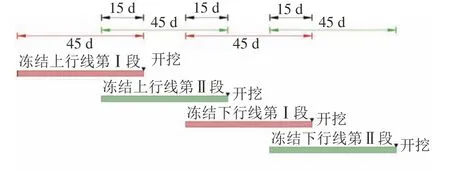
图3 分段冻结试验方案Fig.3 Experiment scheme of segmental freezing construction
双线隧道冻结近接穿越上覆车站引发变形破坏的风险较大,两种冻结方案对上部车站底板产生的冻胀规律尚不明确。为保证冻结隧道施工安全,有必要对两种方案进行模型试验研究,对比不同施工方案引发上覆结构变形规律,为施工提供设计参考。
2 物理模型试验
试验时,物理模型必须满足温度、湿度、应力、位移等一系列相似准则。1980年,Jumikis对人工冻结过程中的相似准则进行了研究,推导了诸多相似准则,使模型试验成为一种研究人工冻结规律的有效方法;1990年,崔广心教授对煤矿建井过程中的人工冻结相似准则进行了研究,并研发了冻结相似模拟试验台[16–17]。基于以上研究,试验推导了人工冻结下穿上覆结构工况下的各参数相似准则方程。
2.1 相似准则
1)低温盐水从土体中吸收热量,然后将孔隙水冻结成冰,温度场的相似准则方程[16,18]可以表示为:
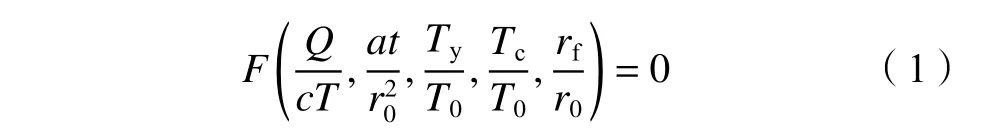
式中:Q为单位土体的潜热,J/kg;c为土体比热容,J/(kg·℃);T为温度,℃;a为热扩散系数,m2/s,t为时间,s;r0为径向坐标,m;rf为冻结管的外半径,m;T0为初始温度,℃;Ty为土体的冰点,℃;Tc为冻结管的表面温度,℃。
试验土体取自于现场,试验过程中重新配置,调整密实度和含水量与原状土一致。故可认为内摩擦角、泊松比、孔隙率等参数与原状土相同。
湿度场的相似准则方程[19]为:
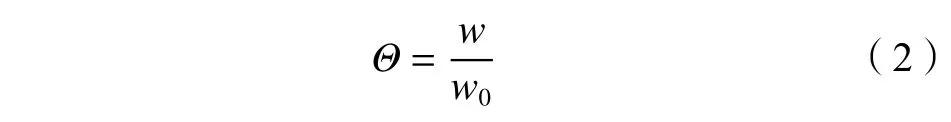
式中:w为土体冻结后的湿度,%;w0为土体原始湿度,%。由湿度准则可知,水迁移过程与导热过程在数学上相似,两者均遵循傅里叶准则,因此在几何相似的条件下,只要温度场相似,湿度场可以达到“自模拟”而相似[17]。
2)冻结和开挖引起土体变形,应力及位移场可以用无量纲形式表示[20],即:
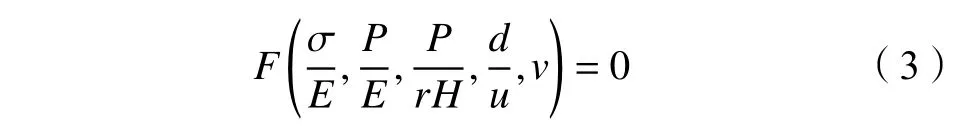
式中:σ为应力,Pa;E为弹性模量,Pa;P为载荷,N;r为堆积密度,kg/m3;H为隧道深度,m;d为冻土的厚度,m;u为位移,m;ν为泊松比。
3)结构因冻胀或融沉产生变形。由弹塑性力学可知,结构挠度us与刚度K成反比,即:
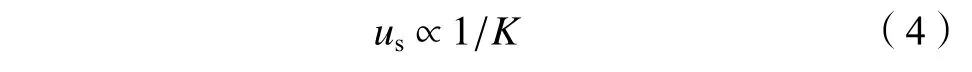
式中:K=EsI;Es为上覆结构底板的弹性模量,Pa;I为静矩,N·m。
基于以上相似准则,各参数的相似比为:
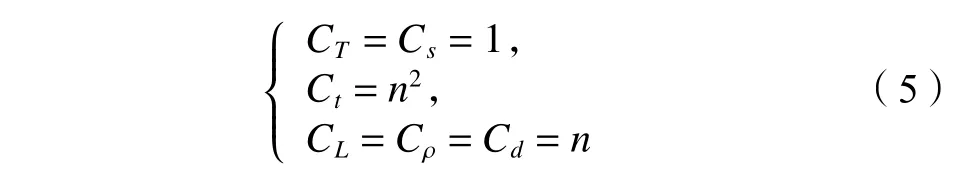
式中,n为常数,CT、Cs、Ct,CL、Cρ和Cd分别为温度、应力、时间、长度、密度和位移的相似比。
2.2 试验设计
根据冻结施工范围及车站尺寸,边界条件取冻结核心区域直径的3~5倍;试验同时考虑模型试验的经济性和可行性,确定模拟施工边界为长×宽×高=75 m×36 m×36 m。设定几何相似比n=1/25,则试验模型的尺寸为3.0 m×1.5 m×1.5 m,隧道模型直径φ=280 mm。冻结温度设定为−28 ℃,冷媒采用体积质量为1 265 kg/m3的CaCl2溶液。时间比例n2=1/625,即模型试验过程中的1 h相当于实际过程的625 h。工程中积极冻结时间设定为45 d,换算得出试验时间为104 min。根据总散热量相等的原则,将实际布设的冻结管路换算为24根φ18的冻结管,材质与工程中冻结管材质相同,布置如图4(a)所示。为实现分段冻结及开挖,在试验土箱两侧布设冻结管,土箱两侧开挖,采用2个配液圈供冷,配液圈A为第Ⅰ区段提供冷量,配液圈B为第Ⅱ区段提供冷量。配液圈A、B上分别安装有控制阀门,可以单独控制隧道Ⅰ、Ⅱ区段的冻结循环。循环后的高温盐水汇集至集液圈返回冷冻机,如图4(b)所示。在全长冻结模式中,第Ⅰ、Ⅱ区段配液圈同时开启;在分段冻结模式中,上下行线Ⅰ、Ⅱ区段配液圈按试验方案错时开启。
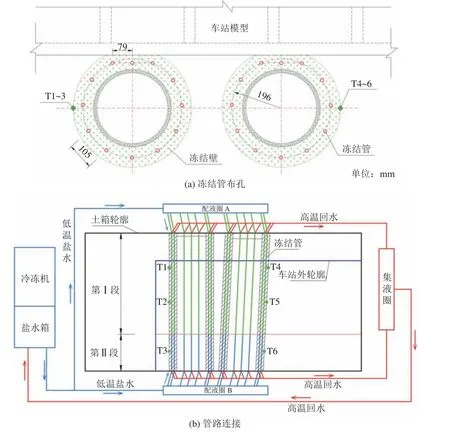
图4 模型试验管路系统示意图Fig.4 Schematic diagram of the pipeline system in the similar simulation experiment
根据相似准则,模型土体的重力密度应为现场土体重力密度的25倍;因模型材料与原型相同,需采用离心[21]或者施加上覆荷载[22–25]的方法满足土体重力密度相似比。试验使用施加上覆荷载方法,根据上覆车站及土体总重量计算得出需加载80 t压力,即反力架上安装两个伺服液压油缸,每个油缸施加40 t压力以满足土体重力密度相似比,使用两块1.5 m×1.5 m的压板将上覆荷载均匀分布在土体上,如图5所示。

图5 模型试验系统示意Fig.5 Schematic diagram of the similar simulation experiment
混凝土车站等比例缩小后容易被上覆载荷压碎,因此,根据刚度相等准则将车站模型材料由C35混凝土改为钢材。顾宝和[26]、孙家乐[27]等认为:由于上部结构的刚度是在施工过程中逐步形成的,上部结构刚度的贡献有限,只有最下面几层的刚度能够发挥,故本次试验取保守值;刚度换算仅考虑结构底板的刚度,不考虑车站上部结构的刚度。通过改变钢底板的厚度以保证刚度相等,继而使变形相等。混凝土和钢的弹性模量分别为31.5和210.0 GPa。车站底板为矩形结构,由矩形的静矩可知:
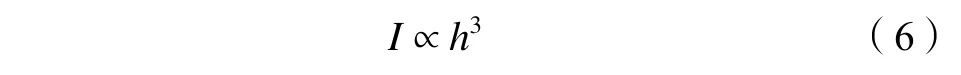
式中,h为车站底板厚度,根据刚度相等准则得出钢制车站底板厚度为21 mm。
采用精度为0.1 ℃的DS18B20微型温度传感器进行监测,将其布设在设计冻结壁的外缘,如图4和6中的T1~T6。在车站底板宽度方向3等分处安装6个精度为0.01 mm的百分表监测底板变形,代号为A1、A2、B1、B2、C1、C2(图6)。土箱开挖区域外侧面为20 mm厚亚克力板,开挖时将亚克力板破拆,使用取芯钻机凿出土体模拟隧道开挖。
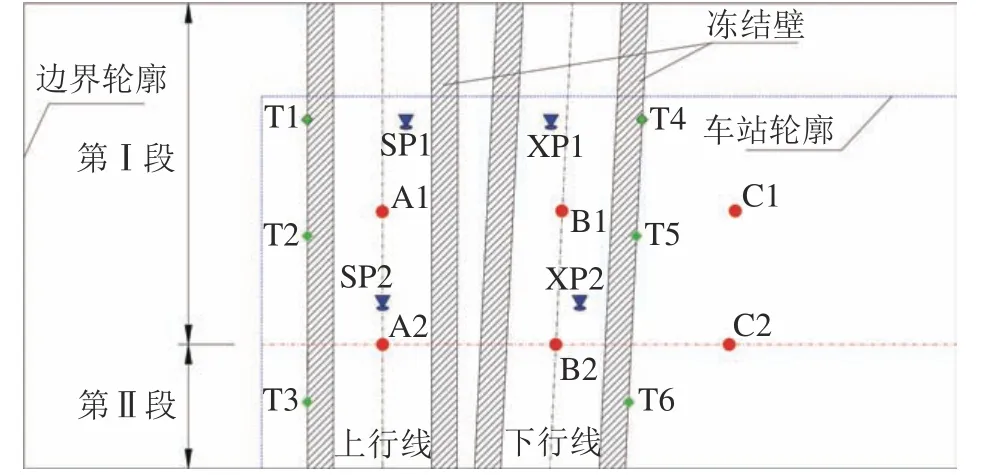
图6 试验开挖顺序及位移传感器位置Fig.6 Excavation sequence and the position of displacement sensors
2.3 试验方案
连接试验各系统,进行3组试验,应变、位移、温度数据均由数据采集系统自动采集。试验于2018年10—12月进行,工程于2018年12月进场施工。
第1组试验为全长冻结试验,加载压力80 t,不分段冻结,不开挖,试验时间为104 min,对应工程实际冻结时间为45 d。
第2组试验分段冻结试验,仅冻结,不开挖,加载压力80 t,各段积极冻结完成以后转入维护冻结,试验时间为315 min,对应工程实际冻结时间为135 d。
第3组试验为分段冻结试验,加载压力80 t,采用分段冻结、分段开挖方法模拟实际工况,开挖模拟采用取芯钻机掘进。试验时间315 min,对应工程实际冻结时间135 d。
3 试验结果及分析
提取温度传感器数据,可得积极冻结后,3组试验冻结壁边缘平均温度分别为–4.60、–4.48和–4.42 ℃,表明分段冻结与全长冻结形成的冻结壁厚度可达到设计厚度。
3.1 全长冻结对车站底板产生的抬升
提取第1组(全长冻结)试验数据,得出车站底板位移传感器数据随时间的变化曲线,如图7所示。
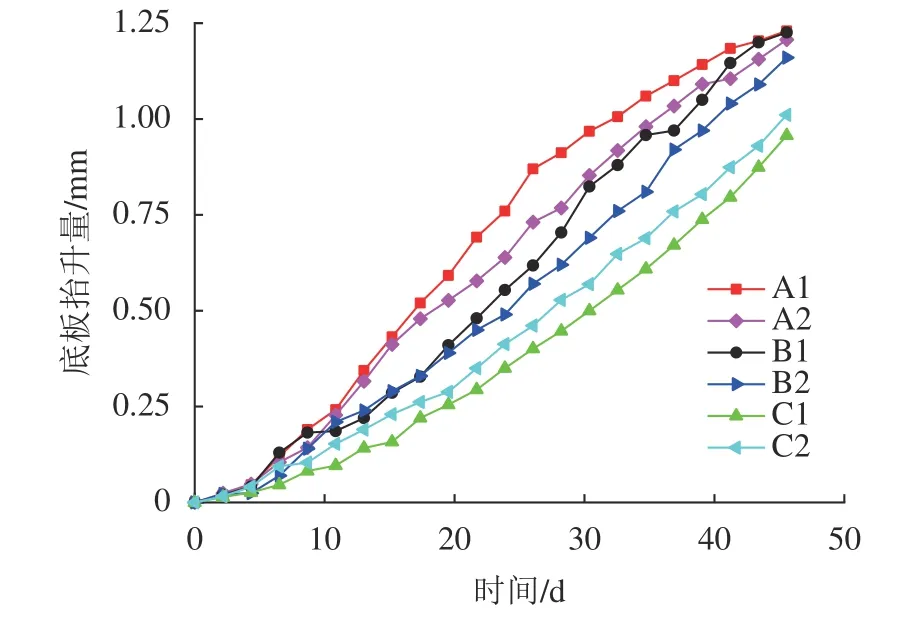
图7 全长冻结模式下车站底板位移随时间变化Fig.7 Displacement of station base slab versus time induced by simultaneous freezing
由图7可知:全长冻结模式下,6个传感器数据偏差不大,但冻结壁正上方的底板抬升位移(A1、A2、B1、B2)大于下方无冻结壁的底板位移(C1、C2);车站底板抬升模式为整体抬升,试验得出抬升平均值为1.2 mm,可以换算得出实际工程平均抬升量为30.0 mm。
3.2 分段冻结对车站底板产生的抬升/沉降
试验得出分段冻结与开挖过程中的车站底板位移量,将试验时间换算为实际施工时间,车站底板在不开挖和开挖工况下的位移曲线如图8所示,位移传感器A2的数据因设备短路舍去。
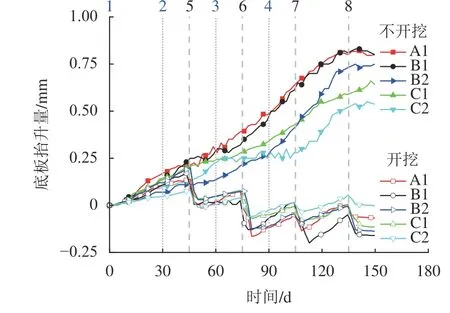
图8 不同施工工序下车站底板位移随时间变化Fig.8 Displacement of station base slab versus time in different construction processes
图8中,竖线1~4分别为冻结上行线第Ⅰ段和第Ⅱ段、下行线第Ⅰ段和第Ⅱ段的开始时间,虚线5~8为开挖上行线第Ⅰ段、第Ⅱ段、下行线第Ⅰ段和第Ⅱ段的开始时间。由图8中不开挖工况下的试验数据可知:上行线积极冻结、下行线未冻结时,下行线上部的车站底板仍然产生抬升,平均抬升位移为0.15 mm,换算后工程抬升量为3.75 mm,平均抬升速度为0.08 mm/d;当下行线积极冻结时,处于维护冻结阶段的上行线上方的底板也产生抬升。试验中,分段冻结模式下的最大抬升位移为0.82 mm,换算为工程中的抬升量为20.50 mm,平均抬升速度为0.12 mm/d,约为全长冻结模式下冻胀位移的68%。分段冻结模式下的积极冻结时间135 d,可知分段冻结可以有效减少上部结构的抬升位移但延长了工期。
由图8中开挖工况下的试验数据可知:隧道开挖引起上覆车站底板产生了明显沉降,但是沉降后,车站底板再次被抬升,使底板位移曲线呈现锯齿形。产生这种现象的原因为:当上行线隧道开挖导致上部车站沉降时,下行线隧道上部底板仍处于积极冻结阶段,冻胀对整体车站仍有较大的作用,因此,开挖区域的上部结构沉降速度逐渐减小并再次抬升,造成上部车站底板的沉降和抬升交替出现。
分段开挖时,使用大功率取芯钻机开挖土体,得出开挖4个区域的平均沉降分别为0.18、0.23、0.17和0.15 mm,相当于工程中的4.50、5.75、4.25和3.75 mm。换算得出工程开挖约8 d后,结构沉降趋于稳定。根据平均沉降量可知,上行线Ⅱ段开挖时沉降最大。这是由于上行线隧道土体开挖后,上覆压力完全由冻结壁支撑,造成下行线开挖后的沉降少于上行线开挖后的沉降。由于试验开挖未考虑支护作用,且实际工程中采用台阶法开挖,试验由于时间相似缩比难以做到相同条件,故该沉降规律仅作为参考。
4 工程实测数据分析
模型试验得出的车站变形规律为后续施工方案的选择提供了重要参考。工程于2018年12月至2020年8月期间完成了双线隧道的冻结与开挖构筑。为准确监测上覆车站底板抬升情况,施工期间在双线隧道上方的车站底板上部布置一系列自动化监测传感器,监测数据实时上传至控制中心。因上部车站施工期间正常运营,无法将传感器全部布置在隧道中心线正上方,布设位置如图6所示。图6中,SP1、SP2位于上行线上方车站底板,XP1、XP2位于下行线上方车站底板。
施工中,为保证冻结质量,对积极冻结时间进行延长,根据冻结壁扩展情况实时调整了盐水流量。监测得出上覆车站底板冻胀变形数据如图9所示,工序时间节点在图中以编号1~8的形式进行了标注。时间节点及工序介绍见表2。
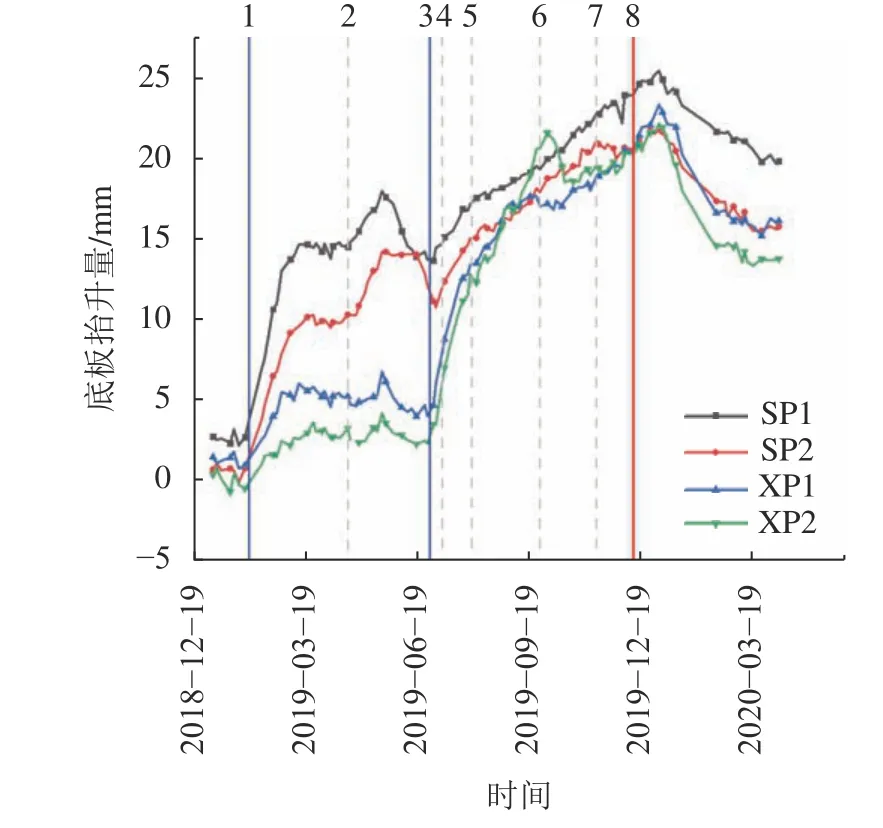
图9 实际施工监测数据Fig.9 Monitored data in actual engineering project
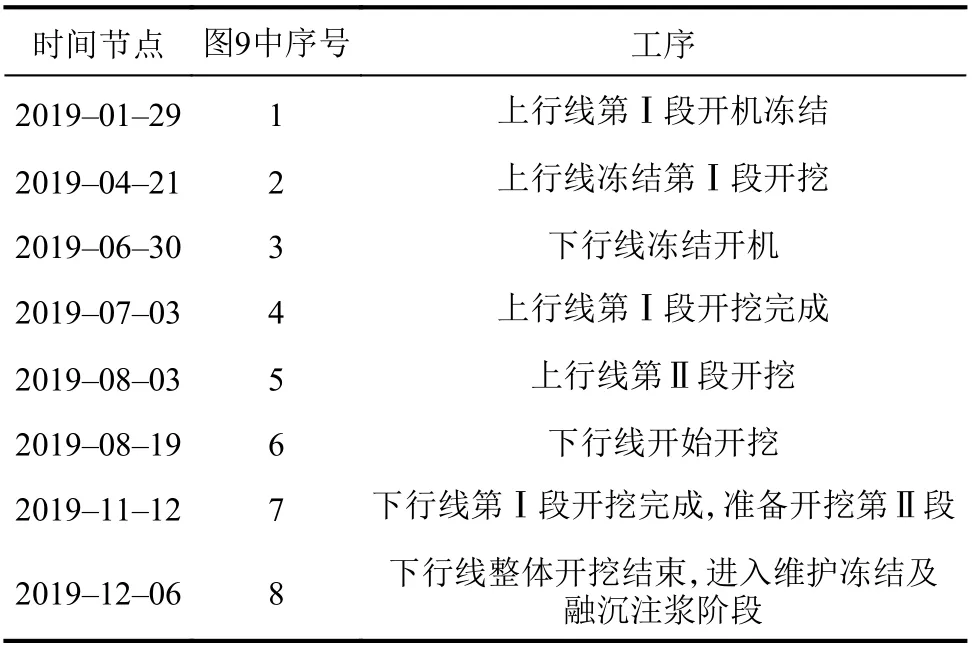
表2 时间节点及工序Tab.2 Timetable and construction procedures
由施工数据可知:
1)在冻结上行线第Ⅰ段时,下行线测点也出现了抬升,但抬升位移较小,如图9中实线1到虚线2段间的曲线所示。该规律与试验得出的规律相同,即分段冻结时车站底板同时抬升。
2)图9中,上行线中实线1到虚线2段间的平滑段是因为工程中采用了取土卸压、三角区卸压、开挖等冻胀控制措施,有效控制了上行线上方车站底板的抬升。
3)上行线第Ⅰ段开挖时,上行线第Ⅱ段正在积极冻结,起始开挖速度低于冻结速度,因此上行线上方车站底板继续迅速抬升;后因开挖致使抬升趋势逐渐平缓,如图9中虚线2到实线3之间的曲线所示。
4)下行线开机冻结后,冻胀位移增长速度较快,此时车站周围土体温度较低,下行线隧道的冻结壁迅速形成,产生较大的冻胀量,加之冻结上行线隧道时车站底板变形蓄能及土体与结构之间的静摩擦力减弱,使车站底板迅速抬升,该规律与模型试验规律相似。由于人工冻土体量大、水分迁移剧烈,施工前期采用的取土卸压、三角区卸压等方法已经难以缓解上覆车站的冻胀抬升。该阶段车站底板最大抬升量为25.41 mm,尽管上行线正在开挖,但车站底板仍产生较大抬升,下行线开挖后抬升趋势减弱,该规律与试验呈现的规律一致。
5)实际工程中未出现试验开挖中的迅速沉降现象,主要原因为:模型开挖时,取芯钻机钻出土体速度较快,在上覆压力作用下,隧道出现较大沉降。实际施工中为避免出现隧道过大沉降,采用了台阶法开挖,将开挖隧道分为上、下两个断面,随挖随支,有效控制了上部结构底板的沉降。
5 结论与讨论
5.1 结论
本文基于上海轨道交通18号线新建隧道冻结穿越地铁10号线国权路运营车站工程工况,依据相似准则进行了模型试验,研究了全长冻结和分段冻结两种模式下,双线水平冻结隧道对上部车站底板冻胀位移变化规律,并将试验得出的规律与工程施工数据进行比对分析,主要得出以下结论:
1)模型试验中,分段冻结模式对上覆结构产生的最大抬升量为20.5 mm,出现在下行线隧道冻结期间,小于全长冻结模式产生的抬升量30.0 mm。分段冻结模式产生的冻胀量小于全长冻结模式,在工期宽松时,应采取分段冻结的方式减小冻胀对上部结构产生的影响;当工期严格时,可以采用全长冻结方式进行施工,同时应注意冻胀对上覆结构的影响。
2)模型试验中,双线隧道冻结下穿运营车站工程中,车站整体刚度较大,基础底板受冻胀作用的抬升模式为整体抬升。模型试验中,采用分段冻结、分段开挖施工时,冻胀抬升和开挖沉降交替产生,使结构基础底板抬升位移曲线呈锯齿形。实际施工过程中,可采用台阶法开挖,随挖随支,保障上覆结构的安全。
3)模型试验中,双线隧道冻结过程中,下行线隧道积极冻结期间的抬升速度为0.12 mm/d,大于上行线冻结时的抬升速度0.08 mm/d。主要原因为:上行线隧道冻结时,车站底板变形蓄能及土体与结构之间存在静摩擦力,减缓了抬升速度;下行线隧道冻结时,蓄能及静摩擦效应均已减弱,且冻结过程中的水分迁移更加剧烈,造成下行线隧道冻结期间更大的冻胀速度和冻胀量。
4)实际工程中采用取土卸压等方法降低冻胀,得出车站底板最大抬升量为25.41 mm。试验得出的上覆车站底板变形规律与施工数据得出的规律相似,在底板抬升趋势、开挖降低冻胀、分段冻结抬升规律等方面具有较好的指导意义,最终工程采用了分段冻结的方法进行施工。
研究为冻结双线隧道冻结近接下穿上覆结构变形规律提供了参考,提高了工程设计的可靠性。试验可以较好地预测施工风险,为本工程和类似工程提供设计参考和数据支撑。
5.2 讨论
1)本次模型试验未考虑融沉影响,实际施工过程中,可以采用跟踪注浆、多点注浆的方法减小融沉造成的地层沉降。
2)随着中国城市地下空间的进一步开发,冻结近接穿越工程数量将进一步增多。诸多冻胀控制措施中,分段冻结可有效控制冻胀的抬升,但其背后的机理仍需进一步探索。在未来研究中,可基于冻胀的时空效应,对分段冻胀与上覆结构的相互作用机理进行深入研究。

