基于模型响应功率谱密度预测的强迫振荡扰动源设备定位法

栾某德，甘德强，李振垚，许 昊，李尚远

（1. 浙江大学电气工程学院，浙江省 杭州市 310027；2. 国家电网有限公司国家电力调度控制中心，北京市 100031）

0 引言

电力系统强迫振荡会造成电力设备过度使用和疲劳、发输电功率受限、电能质量下降、设备故障及损坏等后果，增加系统的运行维护成本；严重时还会造成切机切负荷、继电保护误动作、不受控制的系统解列和大停电等严重后果，甚至在一些极端情况下，还可能造成灾难性后果。

通常，发电机内扰动源所在控制设备的定位称为扰动源的设备级定位，如励磁系统（包括励磁调节器和电力系统稳定器等）、原动机系统（包括原动机和调速器等）。目前，扰动源定位研究主要定位到发电机，为避免直接切除发电机造成功率不平衡并形成新的大扰动，精确到设备级的定位对于精准地切除扰动源更具有实际应用价值。

文献［1-3］将众多强迫振荡案例的扰动源归纳为同步机、原动机及其驱动力矩、调速器、励磁调节器、电力系统稳定器等发电机侧设备，以及负荷波动等产生的周期性扰动，并指出发电机侧的周期性扰动源才是引发强迫振荡最主要、后果最严重的扰动源来源。扰动源定位目前主要有混合动态仿真法［4］、能量函数法［5-6］、行波法［7］、频域特性法［3，8-11］、机器学习法［12］等。文献［4］利用系统模型和测量数据，通过混合仿真法，比较由仿真得到的响应和实际响应的差别，来定位扰动源。文献［5-6］通过确定能量流的传播方向实现了扰动源的定位。文献［7］把强迫振荡视为一种行波，利用行波传播到各发电机的先后顺序定位扰动源。文献［3，8-11］分析强迫振荡响应的幅频和相频特性，利用不同响应的频域关系来定位扰动源。文献［12］用深度学习的方法进行扰动源的定位。文献［13］对现有定位方法进行了详细评述，并且指出目前缺少既有严谨理论基础，又有实际可行性和很强适应性的定位方法，同时，扰动源设备的定位问题也需要解决。

本文基于发电机“模型响应”的定义，推导了发电机模型响应的关系式，给出了模型响应功率谱密度（power spectral density，PSD）的计算步骤（即预测）。模型响应是利用发电机模型和测量所得的边界数据，在给定假设条件下构造的特征响应。通过比较模型响应PSD 和实际PSD 的匹配程度可实现扰动源的定位。通过不同位置扰动源造成的模型响应PSD 和实际PSD 不匹配程度，对扰动源进行精确的设备级定位。

1 模型响应PSD 预测与扰动源定位

1.1 发电机的运算电抗和等值电路

计及发电机纵轴和横轴上的励磁绕组、各阻尼绕组、定子等效绕组，得到磁链方程为：

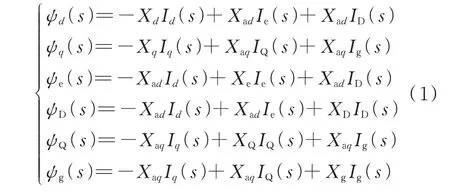
式中：s为拉普拉斯算子；ψd和ψq分别为d、q轴定子等效绕组的磁链；ψe、ψD、ψQ、ψg分别为转子上的励磁绕组、D 阻尼绕组、Q 阻尼绕组、g 阻尼绕组的磁链；Id、Iq、Ie、ID、IQ、Ig分 别 为d轴 等 效 绕 组、q轴 等 效 绕组、励磁绕组、D 阻尼绕组、Q 阻尼绕组、g 阻尼绕组的电流；Xd和Xq分别为d、q轴同步电抗；Xe、XD、XQ、Xg分别为励磁 绕组、D 阻尼绕组、Q 阻尼绕组、g 阻尼绕组的电抗；Xad和Xaq分别为d轴和q轴电枢反应电抗。

定子等效绕组的电压方程表示为：

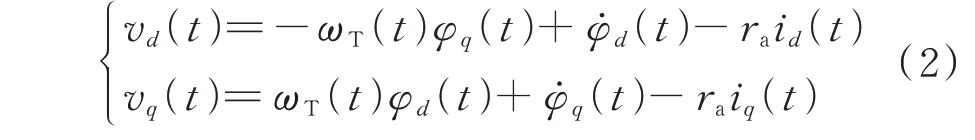
式中：vd(t)、vq(t)和id(t)、iq(t)分别为d轴、q轴绕组电压和电流时域量；ωT(t)为转速时域量；ra为电枢电阻；φd(t)和φq(t)分别为d轴和q轴磁链的时域量。

定子等效绕组中的电磁动态能快速衰减，故可以忽略定子绕组的变压器电势，得到定、转子上绕组的电压平衡关系为：

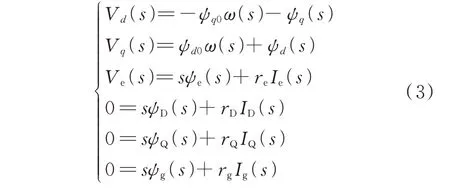
式中：Ve为励磁电压；Vd和Vq分别为d轴等效绕组和q轴等效绕组电压；ψd0、ψq0、Vd0、Vq0分别为相应变量初值，且ψd0=Vq0，ψq0=-Vd0；re、rD、rQ、rg分别为励磁绕组、D 阻尼绕组、Q 阻尼绕组、g 阻尼绕组的电阻；ω为转速。

强迫振荡稳态响应中不含初始项，故式（1）和式（3）中忽略了与初始状态量有关的项。根据式（1）和式（3），用Id和Ve来表示Ie和ID，并代入式（1）的d轴磁链方程中，可得：

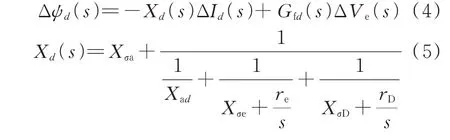
式中：Xd(s)为d轴运算电抗［14］；Gfd(s)为定子到磁场的传递函数；Xσe、XσD、Xσa分别为励磁绕组、D 阻尼绕组、定子绕组的漏抗；Δψd、ΔId、ΔVe分别为相应变量的偏差，因为强迫振荡研究时各变量需用偏差量的形式表示，下同。

类似的，q轴定子绕组磁链可表示为：

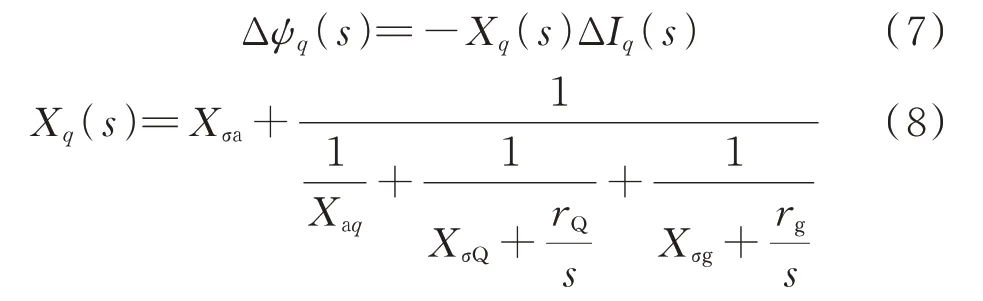
式中：Xq(s)为q轴运算电抗［14］；XσQ和Xσg分别为Q阻尼绕组、g 阻尼绕组的漏抗；Δψq和ΔIq分别为相应变量的偏差。

由式（5）和式（8）可见，Xd(s)和Xq(s)可用如图1 所示等效电路图来阐释。

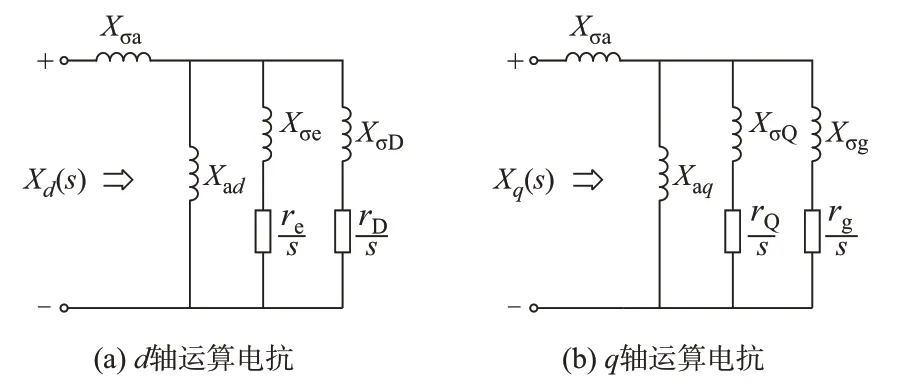
图1 运算电抗的等值电路Fig.1 Equivalent circuits of operational impedances

运算电抗根据发电机模型及参数可以得到，也可以应用适当的频率响应测试法获得。根据运算电抗，可以进一步定义常用的发电机d轴和q轴实用参数。例如，d轴同步电抗Xd定义为s→0 时的Xd(s)，即稳态运行时定子d轴电路呈现的内电抗；d轴暂态电抗X'd定义为D 绕组支路开路（忽略D 绕组）、re=0 时的Xd(s)；d轴次暂态电抗定义为rD=0、re=0 时的Xd(s)；类似的，可以得到q轴实用参数。

运算电抗的概念将为发电机模型响应的定义提供理论基础；在不能直接测量励磁电压时，间接获取励磁电压也需要用到运算电抗的概念。

1.2 发电机模型响应

1.2.1 发电机模型响应的推导

根据运算电抗的概念，可以进一步定义发电机模型响应。将式（3）中的定子电压写为增量形式：

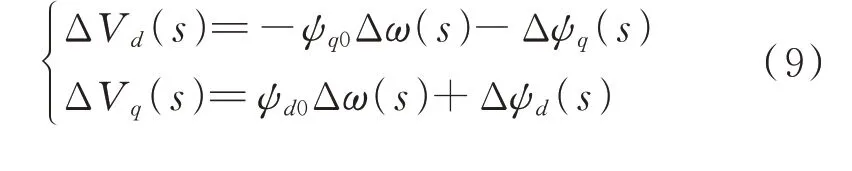
式中：Δω、ΔVd、ΔVq分别为相应变量的偏差。将式（4）和式（7）代入式（9）可得：

发电机电磁转矩偏差ΔTe的拉普拉斯运算形式为：

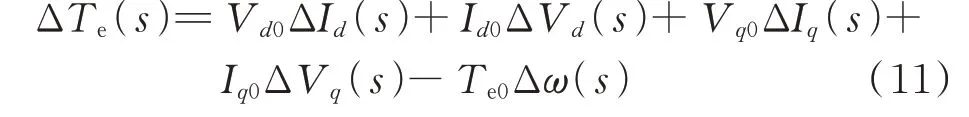
式中：Id0、Iq0、Te0分别为相应变量初值。

结合式（10）和式（11），可以得到：

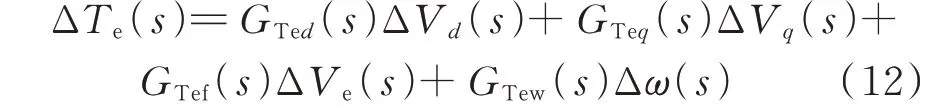
式中：GTed(s)、GTeq(s)、GTef(s)、GTew(s)为传递函数项，具体表达式见附录A。

用Ggov来描述原动机系统传递函数，调速器反馈信号为转速；用Gavr(s)和Gpss(s)分别表示励磁调节器和电力系统稳定器传递函数，电力系统稳定器的反馈信号为转速。假设原动机输出的机械转矩和励磁机输出的励磁电压中分别存在周期性扰动fM和fE，此时机械转矩偏差ΔTm和励磁电压偏差ΔVe可以分别描述为：

式中：Pt0和Vt0分别为机械功率、机端电压的初值。

将式（12）至式（14）代入发电机转子运动方程式（15）中，获得转子角偏差Δδ的表达式为：

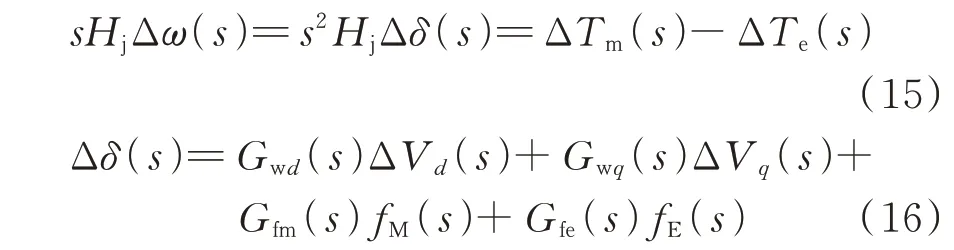
式 中：Hj为发电机惯性时间常数；Gwd(s)、Gwq(s)、Gfm(s)、Gfe(s)为传递函数项，具体表达式见附录A。

由于vd(t)和vq(t)与发电机端电压的幅值和相角有如下关系：

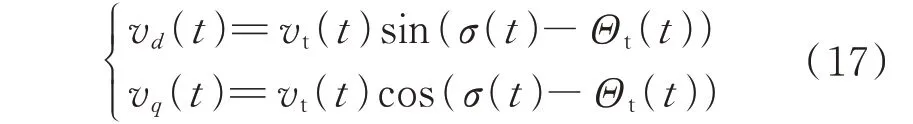
式中：vt(t)和Θt(t)分别为发电机端电压的幅值和相角时域量；σ(t)为转子角时域量。

结合式（16）和式（17），可得转子角偏差Δδ的表达式为：

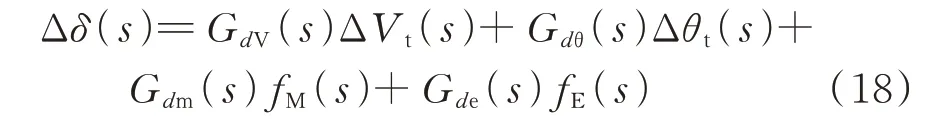
式中：ΔVt和Δθt分别为发电机端电压的幅值和相角的偏差；GdV(s)、Gdθ(s)、Gdm(s)、Gde(s)为传递函数项，具体表达式见附录A。

根据式（18）可得Δω(s)=sΔδ(s)，代入式（14），可得ΔVe的表达式为：

式 中：GEV(s)、GEθ(s)、GEm(s)、GEe(s)为 传 递 函 数项，具体表达式见附录A。

若调速器和电力系统稳定器采用其他信号作为反馈信号，推导类似。将式（18）和式（19）中转子角、励磁电压含fM和fE的项称为强迫项，含电压分量的项称为因变项。只有包含周期性扰动的Δδ和ΔVe中才会含fM和fE项，代表由发电机2 类不同控制系统产生的周期性扰动源。扰动源发电机响应中显性存在周期性扰动相关的强迫项；而发电机不是扰动源时，内部不存在扰动源fM和fE，故响应中不再显性含有强迫项。强迫项和因变项的分类，在将发电机强迫振荡归因于内部扰动源和外部电网影响的归类中，具有关键作用。

如果发电机系统内不含有周期性扰动，则可以将其转子角偏差和励磁电压偏差分别描述为：

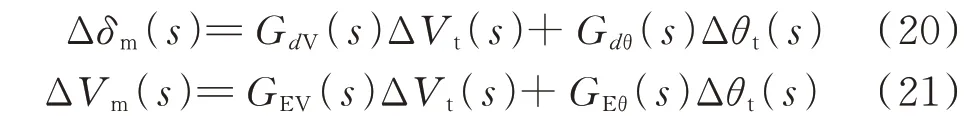
式中：Δδm和ΔVm分别为转子角偏差和励磁电压偏差的模型响应。

电压及其分量即为发电机的边界数据。本文将式（20）和式（21）给出的转子角和励磁电压关于电压分量（幅值和相角）的关系式称为转子角和励磁电压的模型响应。模型响应表示发电机所接入的电网振荡导致的发电机响应因变项，是不含周期性扰动的机组根据数学模型就可以确定的响应部分。若忽略发电机的非线性特性，则不含周期性扰动的发电机模型响应和实际信号是相等的；而扰动源机组含有的强迫项，会导致其模型响应和实际情况不再一致。本文计算发电机响应的PSD 来比较模型响应和实际信号是否吻合。

1.2.2 模型响应的状态空间计算法

针对某台发电机及其控制单元，对其进行线性化，可获得状态空间方程为：

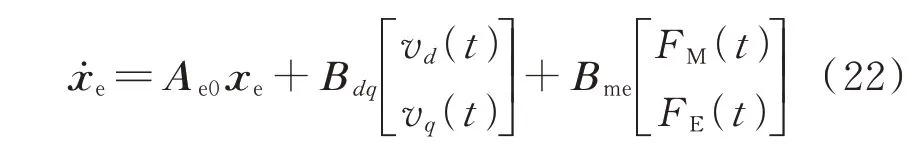
式中：xe为状态向量；Ae0为系统矩阵；Bdq和Bme为输入矩阵；FM(t)和FE(t)分别为原动机输出的机械转矩和励磁机输出的励磁电压中分别存在的周期性扰动时域量。

通过式（17）中不同坐标系下电压分量关系，可以将式（22）表示为：

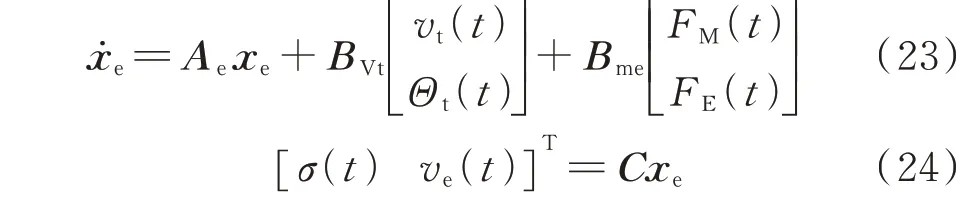
式 中：Ae为系统矩阵；BVt为输入矩阵；C为输出矩阵；ve(t)为励磁电压时域量。

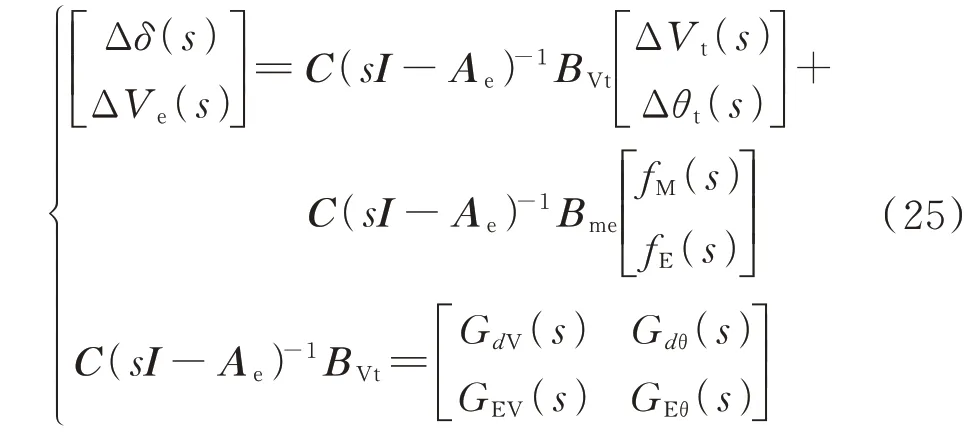
对式（23）和式（24）进行拉普拉斯变换，可得：式（22）用发电机电流d轴分量和q轴分量时域量id(t)、iq(t)描述，类似的，可获得采用机端电流幅值时域量it(t)和相角时域量βt(t)表示的模型响应。

1.3 发电机模型响应的PSD 预测

式（18）和式（19）的发电机响应表明，扰动源发电机响应中除包含模型响应外，还含有强迫项，因此，模型响应和实际信号不相等，但非扰动源发电机响应中不含强迫项，故模型响应与实际信号相等，从而可以将判断发电机内是否含有扰动源的问题转换为衡量模型响应和实际信号是否相等。本文通过计算信号的PSD，然后根据频域的PSD 判断模型响应和实际信号是否匹配，以辨识发电机内周期扰动源的存在性。强迫振荡响应是周期信号，是功率信号，PSD 分析是评估功率信号在频域能量分布的恰当方法，PSD 的定义可见文献［15］。

这里将针对式（20）转子角表达式，利用发电机端电压及其PSD，推导转子角模型响应PSD 的预测值。令GdV(s)和Gdθ(s)的单位冲击响应为gdV(t)和gdθ(t)，将端电压和单位冲击响应w(t)、g(t)分别表示为：

式中：I为单位矩阵。

式（25）等号右侧第1 项是Δδ和ΔVe的模型响应，与 式（20）和 式（21）相 同，GdV(s)、Gdθ(s)、GEV(s)、GEθ(s)也与式（20）和式（21）相同；等号右边与fM和fE有关的项仅出现在扰动源发电机中。若

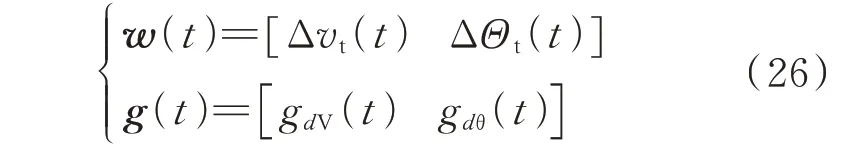
Δδm的时域表达式为：

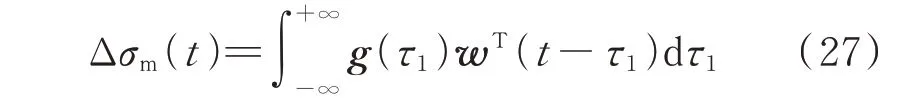
根据式（27），可得Δσm(t)的自相关函数为：

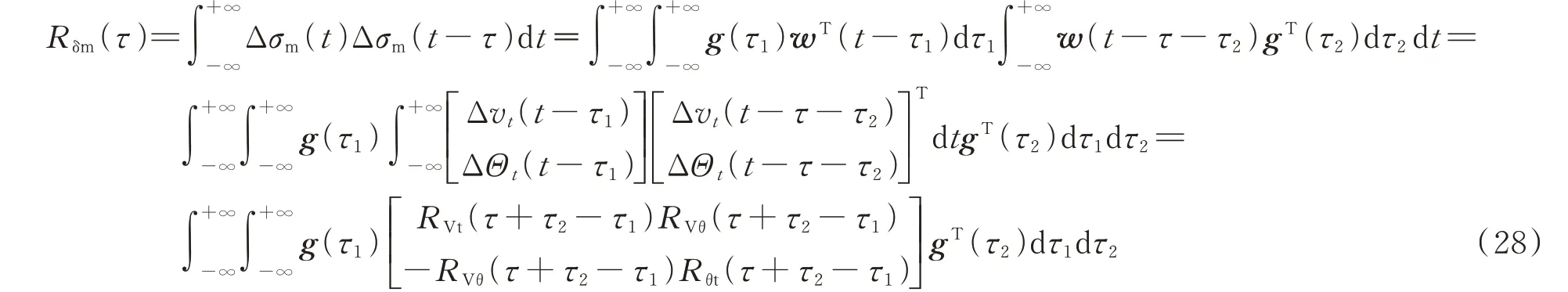
式中：Rδm、RVt、Rθt分别为转子角模型响应、机端电压幅值、机端电压相角的自相关函数；RVθ为发电机端电压幅值和相角的互相关函数。

根据PSD 的定义有：

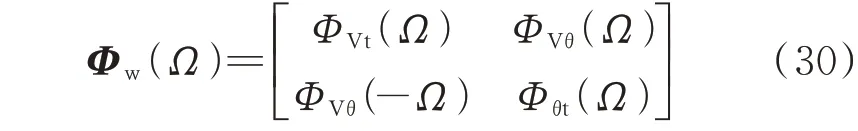
式中：Φδm(Ω)、ΦVt(Ω)、Φθt(Ω)分别为转子角模型响应、发电机端电压幅值、发电机端电压相角的PSD；ΦVθ(Ω)为发电机端电压幅值和相角之间的互功率谱密度；Ω为角频率。

也可将式（29）展开，得到转子角模型响应Δδm的PSD 为：

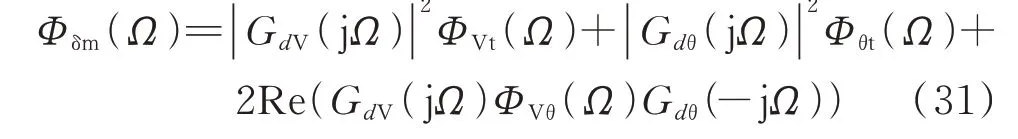
式中：Re（·）为求实部函数。

同理，可得励磁电压模型响应ΔVm的PSD 为：

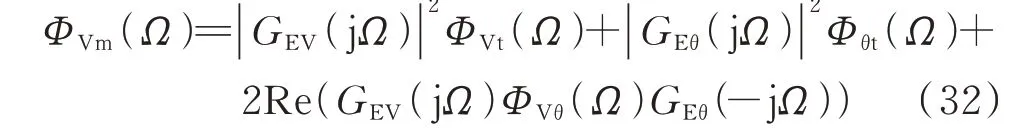
式中：ΦVm(Ω)为励磁电压模型响应的PSD。

式（31）和式（32）将模型响应PSD 表达为电压分量PSD 共同决定的形式，建立了电压各分量与模型响应之间的PSD 耦合关系。根据式（10）和类似归纳，也可将各变量表达成ΔId和ΔIq的函数，最终建立用电流幅值和相角描述的Δδm和ΔVm，从而给出用电流分量表达的模型响应PSD。

对于非扰动源发电机，δ和Ve的模型响应等于实际信号，依据式（31）和式（32），可以预测出δ和Ve的模型响应PSD，且预测值等于实际信号PSD。而对于扰动源机组，以Δδ为例，根据其响应表达式（18），依据PSD 推导过程式（26）至式（29）可得此时Φδ(Ω)的公式如附录A 式（A12）所示，一部分Φδm(Ω) 是 转 子 角 模 型 响 应 的PSD，另 一 部 分Φδf(Ω)是与发电机内周期性扰动源有关的PSD 分量，其会造成Φδ(Ω)和Φδm(Ω)不相等。因此，对扰动源发电机，模型响应PSD 和实际信号PSD 不会相同。对于扰动源发电机，δ和Ve依据式（20）和式（21）计算得到的模型响应PSD 不再等于δ和Ve的实际PSD。扰动源的存在，导致δ、Ve和机端电压的关系不再如式（20）和式（21）所述，而是如式（18）和式（19）所示，包含了扰动源的影响。如果仅用ΔVt、Δθt来表述Δδ和ΔVe，其系数关系也不再是式（18）和式（19）中所示的GdV(s)、Gdθ(s)、GEV(s)、GEθ(s)，这些系数会随着扰动源fM和fE的变化而变化。

针对所有机组，依靠机组模型、电压分量（或电流）和式（31）和式（32），经过计算得到δ和Ve的模型响应PSD，这一过程在本文中称为“模型响应的PSD 预测”。根据推导结论，机组内无周期扰动和各种噪声等干扰时，模型响应PSD 预测值将会与实际信号PSD 精确相等。反之，如果强迫振荡频率处计算得到的模型响应PSD 与实际信号PSD 吻合，则印证机组内没有周期性扰动源；两者若不相等，则印证机组内存在额外的周期性扰动源导致两者不等。计算信号PSD 的方法有周期图法、Bartlett 法和Welch 法等改进的周期图方法等［15］，MATLAB 提供了多种可直接调用的函数来计算信号的PSD。

在实际应用中，考虑到同步机的非线性、噪声、模型不准确等实际影响，会导致不含周期性扰动源的机组模型响应PSD 和实际信号PSD 不能完全相等。计及实际影响，引入判断预测的模型响应PSD和实际信号PSD 不匹配性程度（power spectrum mismatch，PSM）的评估指标。转子角和励磁电压的PSM 分别定义如下：

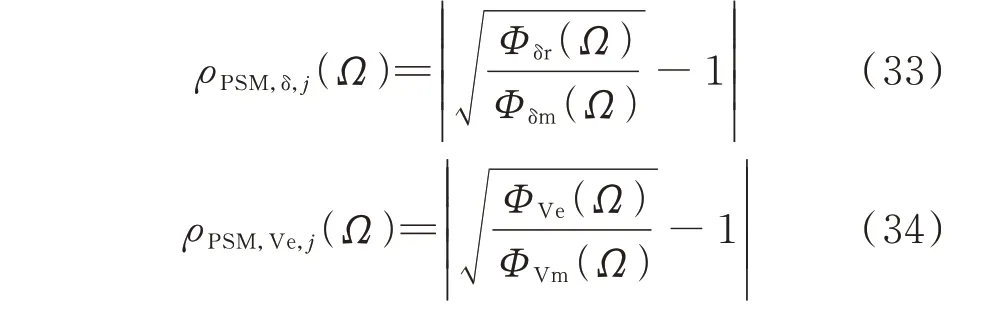
式中：ρPSM，δ，j(Ω)和ρPSM，Ve，j(Ω)分别为第j台发电机的转子角和励磁电压在Ω处的PSM；ΦVe(Ω)和Φδr(Ω)分别为Ve和δ的实际信号PSD。

若发电机内不含周期性扰动源，则ΦVm(Ω)和Φδm(Ω)与ΦVe(Ω)和Φδr(Ω)对 应 吻 合，Ve与δ的PSM 为0。当考虑实际影响因素后，PSM 会是一个较小的值。若发电机内含周期性扰动源，则ΦVe(Ω)和Φδr(Ω) 不 仅 含 有 模 型 响 应PSD（ΦVm(Ω)、Φδm(Ω)），还 含 有 强 迫 项 引 起 的 附 加PSD，使ΦVm(Ω)、Φδm(Ω)和ΦVe(Ω)、Φδr(Ω)间存在明显的差异，故包含周期性扰动的发电机PSM 会是一个显著增大的正值。综上，较大的PSM 能印证发电机内含有引起PSM 变大的附加强迫项，说明此发电机即为扰动源。

ρPSM，δ，j(Ω)和ρPSM，Ve，j(Ω)的定义已经消除扰动源幅值对PSM 的影响；不同频率响应在频域是解耦的，显然各频率处PSM 不会受扰动源频率的影响。因此，PSM 的定义不受扰动源幅值、频率等影响。另外，实际影响因素是随机的，不会产生周期性响应，其功率谱在整个频段是扁平的，每个频率处都较小，当考虑实际因素时，实际因素造成的误差很小，甚至可忽略，在算例部分也会验证。

1.4 励磁电压的重构

本文所提出的定位方法中需要使用发电机转子角和励磁电压等信号，这些信号可以从发电厂获取。现代电网广泛安装的同步相量测量单元（synchrophasor measurement unit，PMU）也会对转子角、转速、励磁电压等信号进行实时采集、传输和监控。对于励磁电压测量单元仍未配备和投入运行的机组，可根据发电机端电压幅值和相角时域量vt(t)、Θt(t)，电流幅值和相角时域量it(t)、βt(t)，转子角σ(t)间接获取和重构励磁电压。结合式（3）和式（4）有：

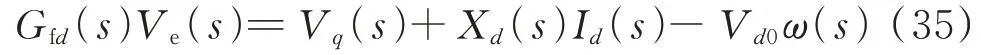
根据vq(t)和id(t)与端电压和电流的关系：

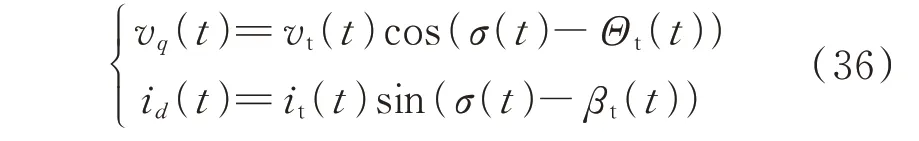
根据式（35）和式（36），可得Ve的频域重构公式如下：

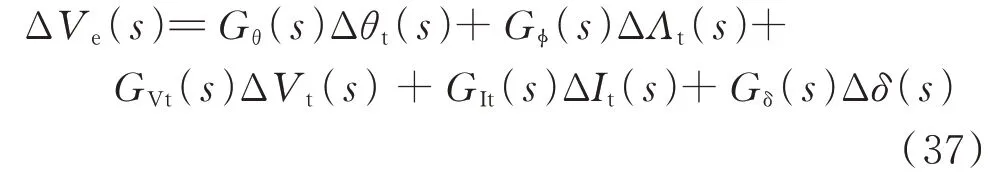
式中：Gθ(s)、Gϕ(s)、GVt(s)、GIt(s)、Gδ(s)为传递函数项，具体表达式如附录A 所示；ΔIt和ΔΛt分别为发电机端电流幅值和相角的偏差。

vt(t)、Θt(t)、it(t)、βt(t)、σ(t)是发电机运行监测需要重点关注的数据。根据测量数据，利用式(37)可以获得Ve的频谱和PSD。

1.5 扰动源的控制设备定位

为实现精准消除扰动源，应该进一步定位到产生扰动源的控制器。虽然Ve和δ的振荡是由各自所在的励磁系统和原动机系统分别直接驱动的，但这2 个控制系统中的任一控制系统中存在扰动源都必然会引起Ve和δ中都出现强迫项。然而，不同控制器的周期性扰动对Ve和δ强迫项的作用强度差异 明 显，这 将 决 定ΦVm(Ω)、Φδm(Ω) 和ΦVe(Ω)、Φδr(Ω)的吻合度和PSM 存在差异。原动机系统和励 磁 系 统 中 的 周 期 性 扰 动 对ρPSM，Ve，j和ρPSM，δ，j作 用程度的差异给辨识产生扰动源的具体控制器提供了信息。以励磁系统扰动源为例，假设第j台发电机的周期性扰动位于励磁系统中，其会显著地作用于Ve强迫项，相比较而言，对δ强迫项的作用强度就很微弱。换而言之，产生周期性扰动的第j台发电机的ρPSM，Ve，j和 其 他 发 电 机ρPSM，Ve，k（k=1，…，j-1，j+1，…，n，n为 发 电 机 台 数）的 区 别 将 比ρPSM，δ，j和ρPSM，δ，k的区别更加显著。至于周期性扰动由原动机系统产生的场合，也有同样的结论。因此，定位扰动源发电机后，根据Ve和δ的PSM，可以进一步根据以下规则辨识产生扰动源的控制器：

模型响应PSD 预测法定位扰动源流程如图2 所示。为判断扰动源发电机PSM 与非扰动源发电机PSM 之间的差别，引入系数α，根据计算经验，一般取α=3 ～5。α根据波形完整性、模型准确性等可以不限于该范围而适当调整。

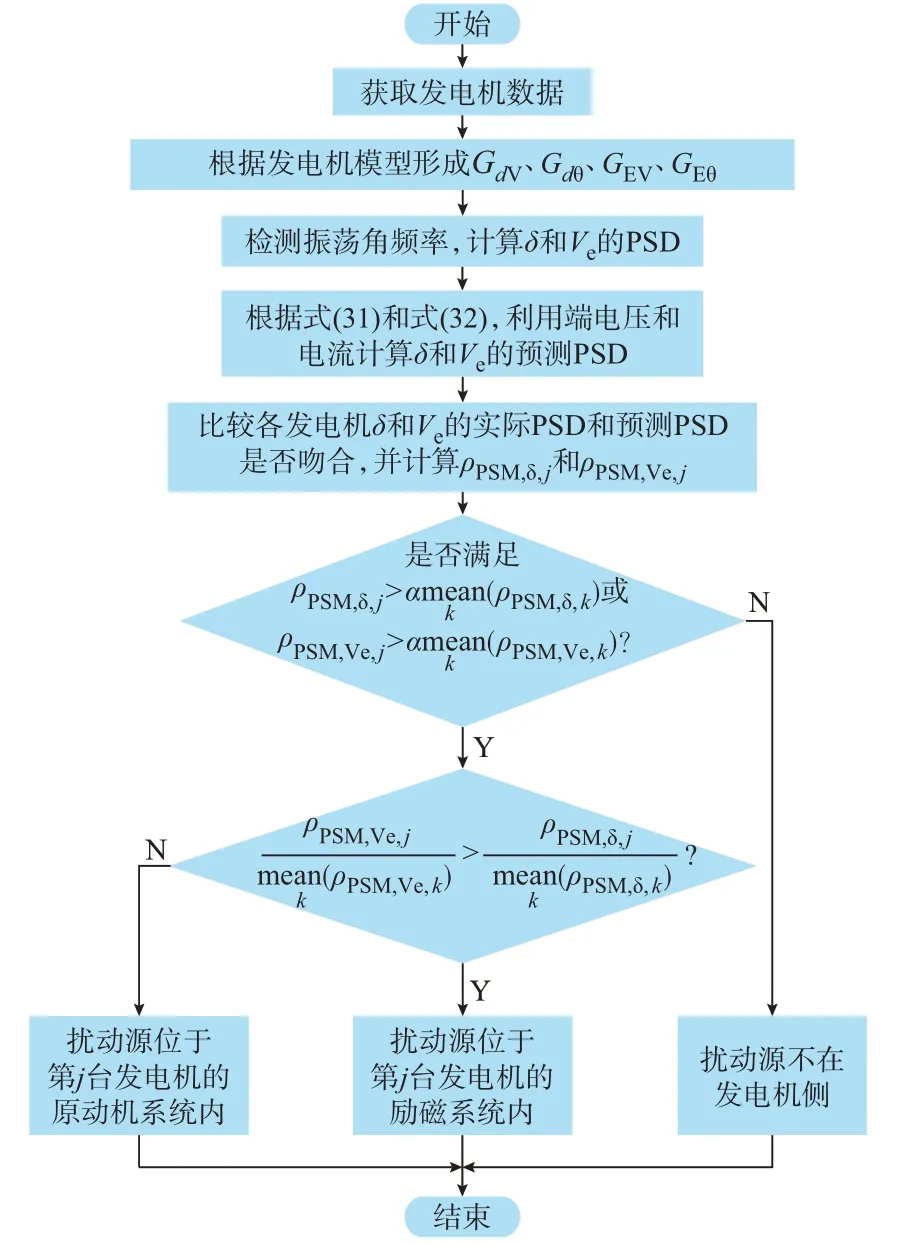
图2 扰动源定位流程图Fig.2 Flow chart for locating oscillation source

2 算例验证

本文基于DIgSILENT PowerFactory 平台进行仿真，以10 机39 节点系统［16］和华北电网［12］为算例验证本文的定位方法。

发电机采用6 阶模型，并都装有励磁调节器、电力系统稳定器、原动机及调速器。系统有2 个弱阻尼模式：一个是0.64 Hz 的区域间振荡模式，阻尼比为1.65%；另一个是1.31 Hz 的本地振荡模式，阻尼比为2.82%。本文以0.64 Hz 的强迫振荡为例，验证本文方法。

2.1 励磁系统扰动源引发强迫振荡

为产生0.64 Hz 强迫振荡，在发电机G6 的励磁系统参考信号（初始值1.49 p.u.）中注入0.15 p.u.、0.64 Hz 的正弦扰动。为模拟负荷波动等类噪声信号的影响，将各负荷的1% 用高斯白噪声代替。图3（a）给出了所有发电机（G1 至G10）的电磁功率振荡曲线。

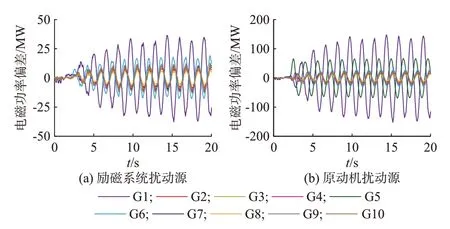
图3 发电机电磁功率Fig.3 Electromagnetic power of generators

首先，对本文提出的模型响应PSD 预测的正确性进行检验，计算Φδm(Ω)和ΦVm(Ω)时忽略模型不准确性、噪声等实际因素。根据式（30）和式（31），获得转子角和励磁电压在所有频率处预测的模型响应PSD 和实际PSD。转子角和励磁电压的预测PSD（Φδm(Ω) 和ΦVm(Ω)）和 其 实 际PSD（Φδr(Ω) 和ΦVe(Ω)）如图4 所示。由图4 可见，除发电机G6 外，其他所有发电机转子角和励磁电压的实际PSD 和模型响应PSD 近乎重合，误差很小，表明对于非扰动源机组，模型响应等于其真实响应，非扰动源发电机响应的PSD 可以由机端电压预测。而扰动源发电机内部由于周期性扰动的存在，两者不再相等，如G6 的实际PSD 和预测PSD 有很大差别。

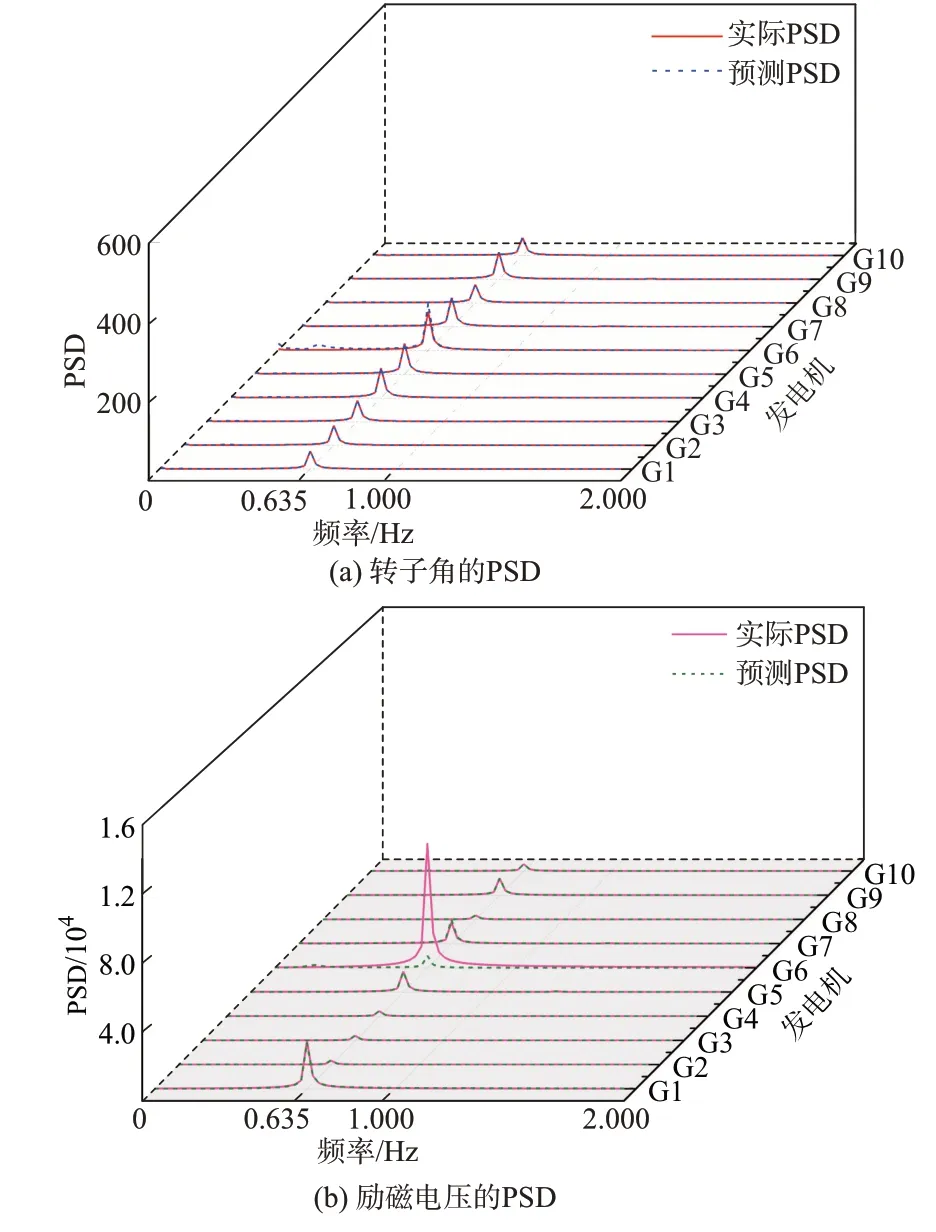
图4 励磁系统扰动下发电机转子角和励磁电压的PSDFig.4 PSD of rotor angle and excitation voltage of generators with excitation system disturbance

图5 给出了在0.64 Hz 的振荡频率处，实际响应和模型响应归一化的PSD。除扰动源发电机G6外，其他发电机的功角和电压的预测PSD 与实际PSD 高度吻合，只有很小的误差。很小的误差是由发电机的非线性引起，例如励磁机饱和就是一个典型的非线性因素。

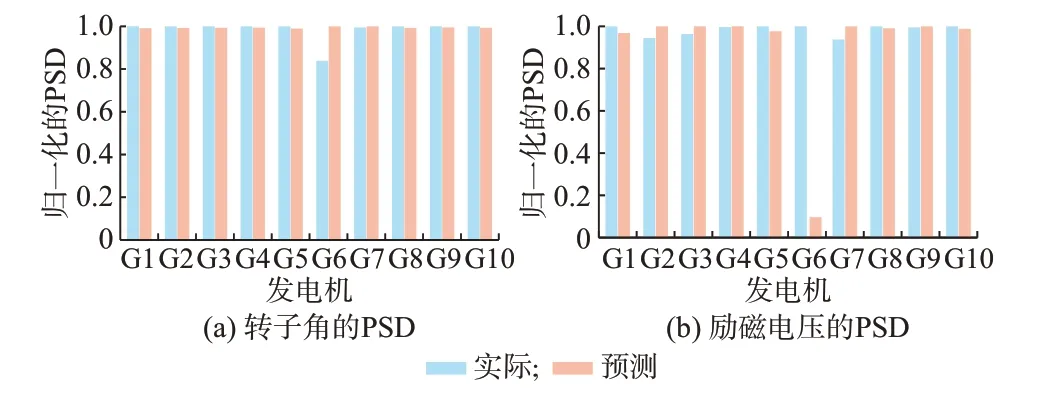
图5 振荡频率处的PSDFig.5 PSD at oscillation frequency

其次，对所提出的方法在更多影响因素下的有效性进行检验，包括发电机模型不准确性、信号噪声等。在模型响应PSD 计算中使用的发电机参数选为含10%以上误差的参数。考虑到噪声的影响，将发电机测量数据vt(t)、Θt(t)、it(t)、βt(t)、σ(t)中加入-30 dB 高斯白噪声。附录B 给出了发电机G10 注入噪声后的电流信号。在这些实际影响因素作用下，计算出0.64 Hz 处预测的模型响应PSD 和实际PSD。图6 给出了归一化的转子角和励磁电压的PSD 和PSM。

图6 励磁系统扰动下各发电机转子角和励磁电压的PSD 和PSMFig.6 PSD and PSM of rotor angle and excitation voltage of generators with excitation system disturbance

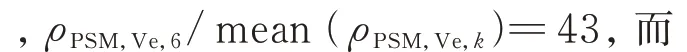
2.2 原动机扰动源引发的强迫振荡

为引发0.64 Hz 的强迫振荡，在发电机G5 的原动机输出（基值为598 MW）中注入0.64 Hz、45 MW的正弦机械功率波动。图3（b）给出了所有发电机的电磁功率振荡曲线。

所考虑的实际因素同2.1 节，用不准确的模型参数和含噪声数据，计算所有发电机的模型响应PSD 和含噪声信号的转子角和励磁电压的PSD，在0.64 Hz 处各发电机功角和电压的预测PSD 和实际PSD 如 图7 所 示。

图7 原动机扰动下发电机功角和电压的PSD 和PSMFig.7 PSD and PSM of rotor angle and excitation voltage of generators with prime mover disturbance

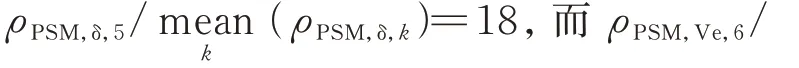
本文方法对方波信号扰动源的有效性表明了定位法对其他形式扰动源的普遍适用性，具体结果见附录B。华北电网算例的结果进一步说明了本文方法的有效性，具体结果见附录C。

3 结语

本文提出了发电机模型响应的概念，并在此基础上通过发电机模型响应PSD 预测，实现具体到发电机和控制设备的扰动源定位。本文从频域角度提出了具有清晰、明确理论基础的扰动源定位法，直观且易于理解。模型响应PSD 的计算中所需的发电机边界数据（电压或电流）和满足要求的发电机模型也较易获取，重点分析实际强迫振荡中振荡明显的发电机即可，且对实际影响因素具有一定的鲁棒性。

本文的扰动源定位是对发电机内部控制器中扰动源引发的强迫振荡进行定位，负荷中的周期性扰动源造成的强迫振荡扰动源定位是未来工作中需重点研究的问题。如何将扰动源定位到更精确的输入信号也需要深入研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。