基于多能互补的医院带菌污水排放预测模型

刘峰

(中国人民解放军总医院，北京100048)

1 引言

由于每个地区经济发展程度存在差异，目前我国城市水管网构建水平也存在差异，管网设计与管理情况毫无规律可言[1-3]。城市水管网中，医院的带菌污水排放十分关键，医院病患较多，带菌污水若处理不当将对城市水资源存在严重威胁，而医院带菌污水排放的高效、准确处理的前提是污水排放的高精度预测[4]。

多能互补属于一类能源政策。多能互补的综合能源供应系统整合了污水热能和电能，实现医院污水排放能源利用最大化，该供应系统分为污水处理、污水源热泵和分布式光伏发电3 个部分。根据差异资源条件与用能目标，使用多样化的能源相互填充，可以降低能源供需矛盾，维护自然资源的均衡，保证生态环境不出现恶性循环。本文构建一种基于多能互补的医院带菌污水排放预测模型，分析医院的多能互补运行机理，对此种情况下的医院带菌污水排放实施高精度预测[5]。

2 基于多能互补的医院带菌污水排放预测模型

医院污水是一种巨大的低温余热源，同时是水-水源热泵的理想低温热源。医院带菌污水排放量巨大，电费占日常运行成本的一大部分，因此设计电储能模型，解决用电问题。医院若采用多能互补的综合能源供应系统，采用污水作为热源，根据污水夏季温度低于室外温度，冬季高于室外温度的特点，实现蓄冷、储热设备内部制冷剂的物态循环变化，消耗少量的电能，从而达到制冷制暖效果的一种技术，具有零污染，稳运行，高效能，不产生废渣、废水、废气和烟尘的特点。

2.1 考虑多能互补的医院综合能源系统

医院属于一种具备冷、热、电3 类符合的综合能源系统，它的储能具有蓄冷、储热、储电和混合储能四类差异模式[6]，多能互补的医院综合能源供应系统整合了蓄冷、储热、储电和混合储能四类差异模式，实现医院污水排放能源利用最大化。

2.1.1 电储能模型

顾及到基于多能互补的医院综合能源系统电池能充放电的最高功率、容量约束和充放电速度与互补约束，电储能能量伴随储能时间的损耗能够省略分析[7-8]。假定Qchar(h)与Qdis(h)依次描述电储能基于h 时刻的充电功率与放电功率；h时刻储能的剩下电量设成ZE(h)，那么：

式中，电储能的充电速度设成αc；电储能的放电速度设成αd；电储能的开始阶段剩余电量设成ZE(0)；电储能充电最高功率设成Qmax；电储能的相互约束设成Qdis(h)×Qchar(h)=0，约束储能状态的一致性。

电储能的经济性大多是基于“低储高发”模式实施套利，基于常规的峰谷电价里，一天仅可以充放电1 回实施套利，盈利空间不大，其功能属于抑制新能源波动、优化电能质量[9]。

2.1.2 蓄冷、储热设备模型

相变储能与显热储能属于常见的冷/热储能模式，显热储能属于典型的储能模式，成本较少。相变储能的成本较高，它的存储热量与释放热量大多是基于材料出现物理状态优化时实现的，温度不存在较大变动[10-11]。和显热储能对比，相变储能存在下述两种优点：储能密度大，基于一样的蓄热量与同一温差条件中，相变材料蓄热相对体积只有显热材料的一半，甚至更少；存/释能时温度恒定，不存在不可控性[12]。

储热和蓄冷模型存在类似性，都存在下述属性：储能、释能过程中具有能量损耗。例如储热而言，它的常规模型是：

式中，h时刻储热装置的剩余热量设成ZH(h)；储热装置的储热与放热速度依次设成αT1、αT0；储热装置通过单位时间后的耗损度设成αT；储热装置的容量最高值设成SHS；h时刻储热装置的储热与放热功率依次设成TT1(h)、TT0(h)；储热装置的储放热功率最高值设成Tmax。

2.1.3 熔融盐压缩空气混合储能模型

由于储能系统内部的能量存在补充性，熔融盐储热的非补燃压缩空气储能系统能够耦合熔融盐储热和压缩空气储能两类模式。此混合系统使用熔融盐储热系统里的热量是涡轮机进口空气加热，完成局部热能变换成电能；并且能够配置电热装置把电能变成热能，最后完成混合储能将热、电两类能量流的四象限工作。

按照混合储能系统的四象限工作机理，假定混合储能的电、热输入功率依次是Qin、Tin，电、热输出功率依次是Qo、To；δ1、δ2依次描述能量输入、输出时间间隔，那么系统模型是：

式中，压缩机与涡轮的速度依次设成αCom、αTur；储热速度设成αHs；涡轮机进口空气加热与电热器速度依次设成αH-E、αHeat。

2.2 基于灰色马尔柯夫的带菌污水排水预测模型

2.2.1 马尔柯夫预测模型

马尔柯夫预测的理论基础为马尔柯夫流程，其表达一种非指定时间序列的动态变动流程。按照马尔柯夫链，把基于多能互补的医院综合能源系统中带菌污水数据序列分为多种状态，将其设成P1，P2，…，Pm，根据时序把转移时间设成h1，h2，…，hm，带菌污水数据序列从状态Pt通过h步变成Pi的几率设成，则：

如果初始状态Pj的初始向量设成B(0)，那么通过t 步转移后：

2.2.2 灰色马尔柯夫预测模型

使用2．2．1小节构建的马尔柯夫预测模型，将医院带菌污水排放量设成时间序列，构建灰色马尔柯夫预测模型。灰色马尔柯夫预测模型的预测步骤是：

相对差值是：

(2) 将相对差值序列构建马尔柯夫模型，获取拟合值，判断带菌污水排放状态几率转移矩阵。因为预测医院带菌污水排放量时，状态界面存在不可判断性，所以选择一组临界值，把非未知的相对差值序列实施计算，获取几率转移矩阵，将非一直数据实施检验，满足率大的便设成转移几率矩阵。本文将界限依次设成-2%、-0．2%、0．2%、2%，把相对差值序列设成5种范围，详情见表1：

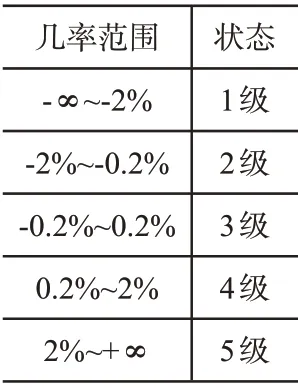
表1 几率状态设定

(3) 获取基于多能互补的医院综合能源系统中带菌污水排放预测趋势后，将相对差值实施马尔柯夫修正，能够获取二次拟合值，以此获取二次残差。

(4) 将构建的灰色马尔柯夫模型实施低误差概率与后验差比检验，若合格便实施医院带菌污水排放预测。

3 实验结果

大连市医科大学附属第二医院2010～2019年带菌污水排放量的整理资料如表2、表3所示，使用2010～2016年的数据实施建模，2017～2019年的数据设成预测检验。

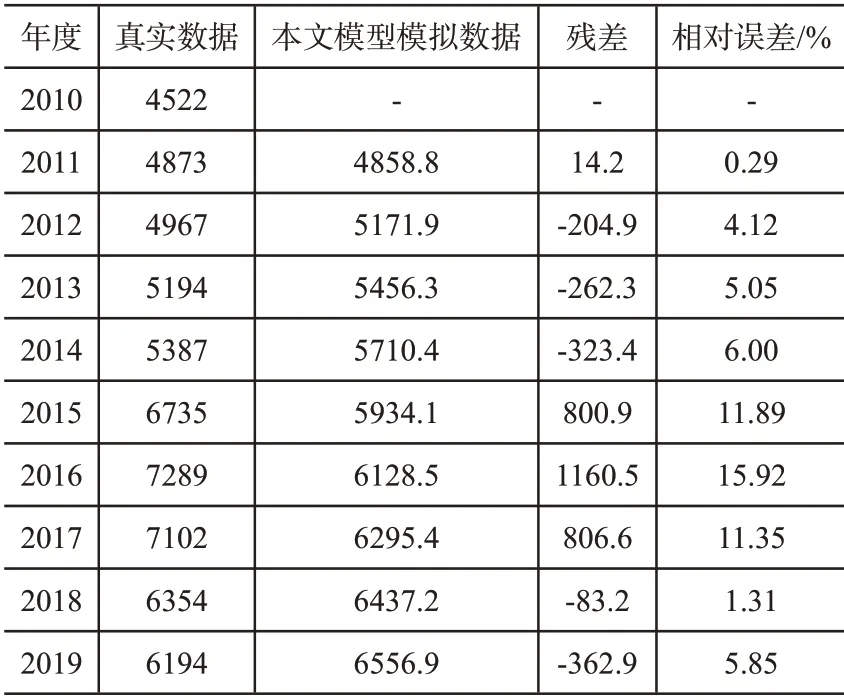
表2 模拟和误差检验表

检验后可知，后验差比值是0．204，相对误差最大值是11．89%，则本文模型可以符合污水排放预测精度的需求。使用本文模型对该医院带菌污水排放预测后，结果如表3所示：

分析表3可知，本文模型预测的相对误差最大值仅有6．05%，预测精度较高，对医院带菌污水排放量的模拟预测存在有效性。

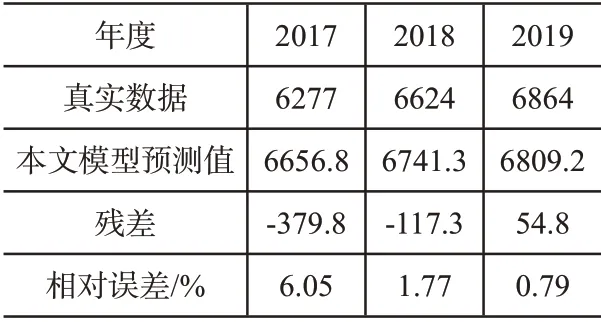
表3 预测结果精度测试

为了深入测试本文模型的应用优势，设定对比模型依次是基于灰色Verhulst 的城市污水排放量预测模型、等维灰数递补动态模型。设定该医院的带菌污水类型依次是病原体污水、重金属污水、消毒剂污水、有机溶剂污水、放射性污水，使用三种模型对该医院2019年的污水排放实施预测，测试三种模型的查全率与查准率，结果如图1、图2所示：

分析图1、图2可知，三种模型预测该医院中病原体污水、重金属污水、消毒剂污水、有机溶剂污水、放射性污水排放时，本文模型的查全率高达99．01%，基于灰色Verhulst的城市污水排放量预测模型、等维灰数递补动态模型的查准率小于本文模型；本文模型的查全率高达0．99，和基于灰色Verhulst 的城市污水排放量预测模型、等维灰数递补动态模型相比，本文模型在预测医院多种带菌污水时，预测范围充分。

采用基于灰色Verhulst 的城市污水排放量预测模型、等维灰数递补动态模型对该医院2010～2019年10年间的带菌污水排放实施预测，并将预测结果和表2结果实施对比，结果见表4：

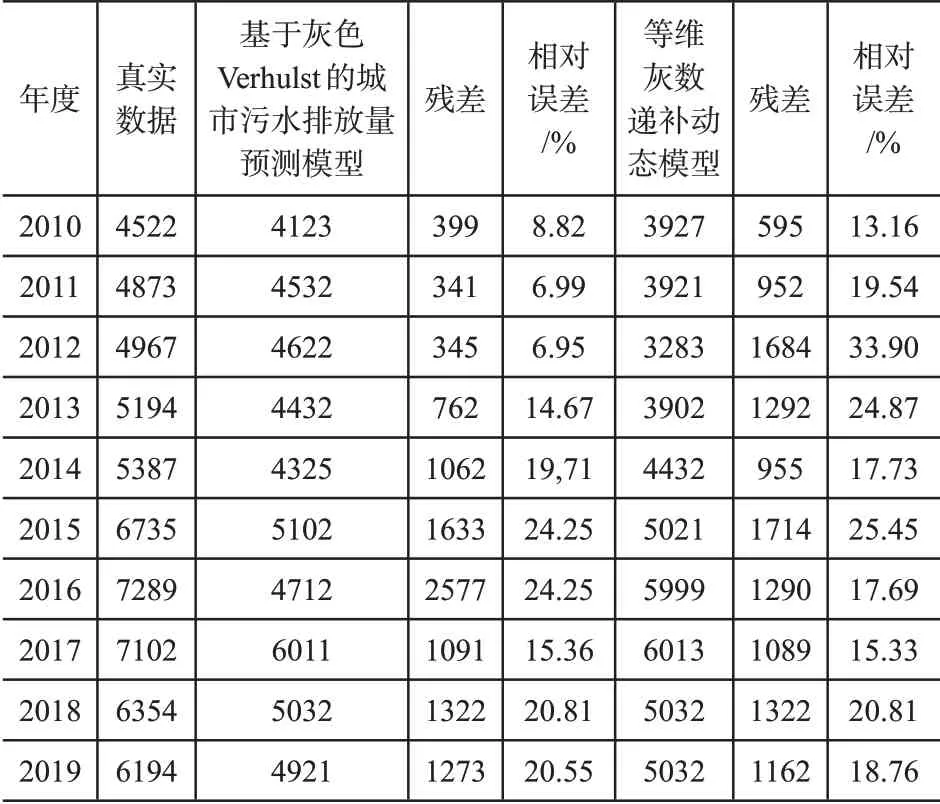
表4 两种对比模型的预测结果

分析表中数据可知，基于灰色Verhulst 的城市污水排放量预测模型、等维灰数递补动态模型对该医院2010年～2019年带菌污水预测后，基于灰色Verhulst 的城市污水排放量预测模型预测结果的相对误差最大值高达24．55%，和本文模型相比，其相对误差高出18．2%；等维灰数递补动态模型预测结果的相对误差最大值高达33．90%，高出本文模型27．85%。由此可知，相比之下，基于灰色Verhulst 的城市污水排放量预测模型、等维灰数递补动态模型的预测精度低于本文模型。

为了测试本文模型的应用效果，将本文模型分别使用在青岛阜外心血管病医院、复旦大学附属肿瘤医院、南方医科大学口腔医院、抚顺市结核病院中，并通过四种医院的满意度判断本文模型的应用效果，结果见图3：

分析图3，青岛阜外心血管病医院、复旦大学附属肿瘤医院、南方医科大学口腔医院、抚顺市结核病院对本文模型的应用效果均高度认可，满意度均大于0．97。

4 结束语

本文构建一种基于多能互补的医院带菌污水排放预测模型，并对大连市医科大学附属第二医院2010～2019年带菌污水排放实施预测，经验证，本文模型的预测精度较高，查全率与查准率均优于基于灰色Verhulst 的城市污水排放量预测模型、等维灰数递补动态模型。当本文模型使用于不同类型医院后，青岛阜外心血管病医院、复旦大学附属肿瘤医院、南方医科大学口腔医院、抚顺市结核病院对本文模型的应用效果均高度认可。由此验证本文模型的有效性与应用优势。