考虑摩擦耗能的桥梁盆式橡胶支座三维有限单元构建

魏思聪，李鹏飞，董振华，梅 波，罗吉庆

(1.交通运输部公路科学研究院，北京 100088；2.广东省公路建设有限公司，广东 东莞 510660)

0 引言

滑动型桥梁支座相较于传统钢铰支座，有可动性好、耐久性高的优点，被广泛应用于国内外各类公路桥梁结构中。其中，盆式橡胶桥梁支座是滑动型桥梁支座的代表之一。现代盆式橡胶支座的滑动面上通常有聚四氟乙烯(PTFE)涂层，此类盆式橡胶支座被称为聚四氟乙烯盆式橡胶支座。聚四氟乙烯化学性质稳定，是一种优秀的工程材料，特别是在与金属材料相互摩擦时，聚四氟乙烯-金属摩擦面上的摩擦系数小于金属-金属摩擦面。所以，支座滑动面上的聚四氟乙烯涂层可以减小支座损耗，提升支座耐久性。

在桥梁结构动力分析中，支座滑动面一般被认为是光滑面，而支座摩擦则被包含进结构阻尼中，通过设置结构阻尼比予以考虑。一些精细化桥梁结构动力分析则采用Coulomb摩擦模型模拟支座摩擦。随着对摩擦力学的深入研究，很多学者指出，钢-聚四氟乙烯界面的摩擦机理与Coulomb摩擦模型所表征的线性摩擦存在较大差异，前者的动摩擦系数并非是一个由界面材料特性确定的常数，而是随滑动速度和界面正压力变化而变化，即存在明显的速变和压变特征，体现出较大的非线性[1]。

在滑动加速度较小和界面正压力较稳定时，钢-聚四氟乙烯界面摩擦可以采用Coulomb摩擦模型表征。但在车辆通过引发振动、风振、地震等公路桥梁振动场景中，钢-聚四氟乙烯界面摩擦的非线性特征对结构动力响应影响较大，应当予以考虑。同时，随着对桥梁支座摩擦研究的深入，部分学者发现桥梁支座摩擦对桥梁自振频率、结构阻尼等振动特性有显著影响[2]。李爱丽、高日[3]，魏标、刘义伟、蒋丽忠等[4]进行不同支座类型桥梁的地震响应分析，讨论了支座摩擦对结构地震响应的影响。王常峰、朱春林、陈兴冲[5]对活动支座摩擦作用对桥梁弹塑性地震方向的影响进行了数值模拟研究。

随着隔振器、阻尼器等减振技术发展以及材料科学进步，很多学者致力于应用非线性数学模型描述振动能量耗散的物理过程，其中就包括滑动摩擦耗能。Mokha和Constantinou等[1]提出了钢-聚四氟乙烯界面滑动摩擦系数的计算方法，并应用改进的Bouc-Wen模型，模拟聚四氟乙烯基础隔振器的动力摩擦响应，其成果被广泛应用。张文芳、程文瀼[6]考虑了滑动速度对动摩擦系数的影响，提出了相应的数学关系式。刘少波、李爱群[7]对泡沫铝-聚氨酯复合材料摩擦阻尼器进行了试验研究，并应用修正的Bouc-Wen模型模拟了试验所得的摩擦滞回曲线。李悦、纪梦为、李冲[8]就温度对板式橡胶支座摩擦滑移性能的影响进行了有限元模拟分析，提出了滑动摩擦耗能与环境温度间的关系。Lomiento等[9]研究了地震激励下滑动支座的摩擦模型。

图1 盆式橡胶支座半剖面图

以上研究富有成效，从不同方面丰富完善了支座摩擦理论，加深了关于支座摩擦对桥梁动力响应影响的理解。但由于结构振动分析中考虑支座摩擦效应所涉及因素较多，计算难度较大，如何充分考虑支座摩擦的速变、压变等非线性特征，以及在工程实践中，有效考虑支座摩擦对结构阻尼的影响，仍需进一步研究。

本研究基于Bouc-Wen滞回模型和以往对钢-聚四氟乙烯(PTFE)界面摩擦机理的研究及相关摩擦试验数据，针对公路桥梁振动场景，对盆式支座的滑动摩擦进行分析，构建了一套完整描述桥梁盆式支座任意方向滑动摩擦的数学模型，并基于该数学模型，开发了一种适用于桥梁有限元动力分析的三维盆式支座有限单元。

1 盆式橡胶支座钢-聚四氟乙烯滑动面摩擦机理

以往摩擦试验显示[1，10-11]，钢-聚四氟乙烯滑动面上的滑动摩擦存在两个阶段：相对滑动发生前的静摩擦和相对滑动发生后的动摩擦。相对滑动发生前，界面处于固结状态(静摩擦)，静摩擦力随外力增大而增大，直至达到静摩擦极限Fs,max=μs,maxN，μs,max为最大静摩擦系数，由界面性质决定。随后，静摩擦力被克服，界面进入滑动状态(动摩擦)，滑动摩擦力Fk=μkN，μk为滑动摩擦系数。这一过程被称为“固结-滑动状态转变 (stick-slip transition)”。

Mokha和Constantinou等学者的早期试验研究显示[1]，钢-聚四氟乙烯滑动面的滑动摩擦系数并非如Coulomb摩擦理论所假设，在滑动过程中为恒定常数，而是具有速变性和压变性的特点。Constantinou等提出，滑动摩擦系数可表示为如式(1)所示的速度的函数：

(1)

式(1)并未体现出滑动摩擦系数的压变性特点，Constantinou等[1]给出了4种压力条件下，μmax，μmin和α的取值，如表1所示。

表1 不同压力下μmax，μmin和α的取值

作用在支座顶部的压力随桥梁竖向振动而连续变化，这种参数取值方法，显然，无法满足桥梁振动时任意时刻的摩擦系数计算。本研究对表1数据，采用压力p的对数函数和二次多项式函数进行拟合，得到式(2)参数取值的连续表达式，具体拟合过程详见文献 [12]。

μmax=-0.033 27ln(p)+0.178 2，μmax=-0.009 356ln(p)+0.043 62，α=-2.39×10-5p2+0.001 2p+0.015。

(2)

2 盆式橡胶支座三维有限单元构建

2.1 盆式橡胶支座摩擦数学模型

2.1.1 Bouc-Wen滞回模型与钢-聚四氟乙烯界面摩擦固结-滑动转变过程模拟

Bouc-Wen滞回模型是一种常用的描述黏弹性材料滞回曲线的模型，由Bouc[13]首先提出并由Wen[14]在随机振动和滞回现象分析中拓展和应用。该模型描述恢复力Fr和变形u之间存在以下黏弹性关系：

Fr=ak0u+(1-a)Dk0z,

(3)

式中，k0为材料初始(弹性)刚度；a=ky/k0为材料完全屈服后刚度；ky为与初始刚度的比值；D为变形屈服极限，z被称为滞回参数。其值由以下微分方程确定：

(4)

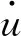
(5)

Bouc-Wen滞回模型可由以下示例解释，如图2所示，材料完全屈服后，总恢复力Fr,1可表示为：

图2 Bouc-Wen滞回模型的力-位移关系曲线

Fr,1=kyu1+Fy-kyD，

(6)

式中，u1为材料完全屈服时的变形；Fy为材料的屈服极限力;Fy=k0D。记ky为k0的线性函数，即ky=ak0，式(6)可写为：

Fr=ak0u1+(1-a)Dk0。

(7)

比较式(3)和(7)可以发现，滞回参数z取值±1时，材料进入完全屈服状态。而|z|<1时，材料处于由线弹性状态向完全屈服状态转变的过程中。因此，滞回参数z可以被视为一个状态控制参数，z的取值确定了材料处于何种工作状态，以及材料展现出何种变形方式。

钢-聚四氟乙烯界面摩擦在发生界面相对滑动前，需要克服最大静摩擦力，由固结状态转变为滑动状态。这一过程在考虑支座摩擦的桥梁振动分析中起到控制性作用。如果采用Coulomb摩擦模型考虑这一过程，则需要建立一个分段函数，将滑动力和最大静摩擦力的比值作为判定条件，确定支座界面是否发生滑动，如图3(a)所示。当桥梁振动分析中自由度较多，支座滑动方向不确定时，Coulomb摩擦模型需要不断判定界面是否发生滑动，将增加数值计算量，并造成收敛困难。同时，在经典Coulomb模型中，支座固结-滑动状态转变是发生在一瞬间的，无法模拟盆式橡胶支座发生宏观相对滑动前，由于聚四氟乙烯层发生剪切变形而产生的钢-聚四氟乙烯界面微小相对位移[1]。

为解决Coulomb摩擦模型在钢-聚四氟乙烯界面摩擦模拟中存在的上述问题，考虑Bouc-Wen滞回模型中滞回参数z具有状态控制的特点，本研究采用Bouc-Wen滞回模型参数z实现摩擦界面的固结-滑动状态转变控制。同时，由于参数取值z是连续的，通过调整式(3)参数D的取值，可以较好地模拟出盆式橡胶支座发生宏观相对滑动前，由于聚四氟乙烯层发生剪切变形而产生的钢-聚四氟乙烯界面微小相对位移。

2.1.2 基于拓展Bouc-Wen滞回模型的盆式橡胶支座摩擦数学模型构建

以动摩擦力Ff,k=μkN代替Bouc-Wen模型中的屈服极限力Fy，得到下式：

μkpAPTFE=k0D，

(8)

式中，p为均匀作用在钢-聚四氟乙烯界面上的压强；APTFE为钢-聚四氟乙烯界面面积。对于钢-聚四氟乙烯界面，μk的取值由式(1)，(2)确定。

将式(8)代入式(3)，设a=0，则Bouc-Wen滞回模型可以用于从数学上表征钢-聚四氟乙烯界面的滑动摩擦，本研究称为拓展Bouc-Wen滞回模型，如下式：

Fr=μkpAPTFEz。

(9)

由式(8)可知，变形屈服极限D可写为：

(10)

根据Bouc-Wen滞回模型中变形屈服极限D的定义和钢-聚四氟乙烯界面发生宏观相对滑动的瞬间力学平衡条件可以推出，在拓展Bouc-Wen模型中，D是滑动前因聚四氟乙烯层剪切变形而产生的钢-聚四氟乙烯界面微小相对位移，通常取值为0.13～0.5 mm[1]，k0为聚四氟乙烯层的抗剪刚度。

当动摩擦系数μk为常量，且k0取值足够大，D取值足够小时，式(9)所示的拓展Bouc-Wen滞回模型与Coulomb摩擦模型相近，如图3所示。

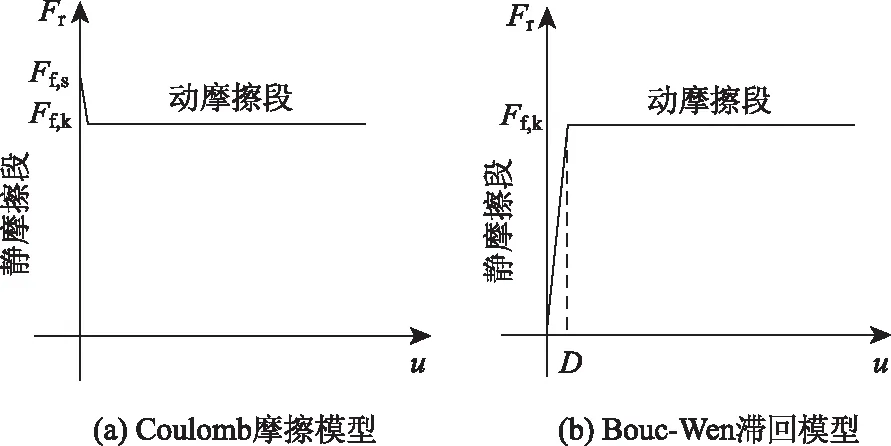
图3 Coulomb摩擦模型和拓展Bouc-Wen滞回模型的摩擦力-位移关系曲线

滞回参数z控制钢-聚四氟乙烯界面的状态。当界面发生宏观相对滑动时，|z|=1，对应Bouc-Wen滞回模型中的材料进入完全屈服状态；当界面没有发生宏观相对滑动时，|z|<1，对应Bouc-Wen滞回模型中材料由线弹性状态向完全屈服状态转变的过程。

2.1.3 盆式橡胶支座摩擦数学模型在滑动平面内的任意方向上的应用

式(9)所示的盆式橡胶支座摩擦数学模型仅适用于方向确定的单向滑动，而实际公路桥梁中使用的多向盆式橡胶支座顶板可以向平面内的任意方向滑动。因此，需要将式(9)所示数学模型从线运动扩展为面内运动，用以表征盆式橡胶支座顶板在平面内任意方向滑动时的摩擦力和滑动位移。

建立平面内正交坐标系，在坐标系内，平面内任意方向滑动可由2个沿坐标轴方向正交的位移自由度表征，如图4所示。

图4 平面内任意方向滑动

Park等[15]和Mosqueda等[16]将Bouc-Wen滞回模型的应用范围从单向运动拓展到平面内正交的双向运动。平面内正交的双向运动条件下的滞回曲线可以由如式(11)的微分方程组描述：

(11)

式(11)也可以写为如下矩阵形式：

(12)

在如图4所示，对于盆式橡胶支座滑动平面内任意方向的滑动，其任意时刻滑动方向与x轴的夹角为θ，则其运动变量在2个坐标轴上的分量为：

(13)

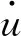
(14)

将式(4)中的参数n取值2，即得到式(14)。式(11)和(14)说明，平面内正交的双向运动条件下的滞回曲线可由任意时刻滑动方向上的滞回参数和合速度描述。

当盆式橡胶支座处于滑动状态下，且x和z方向上的速度分量均不为0时，滞回参数zx和zz取其最大值即1，则下式成立：

(15)

则式(11)可写为一下微分方程组：

(16)

zx=cosθ,

zz=sinθ。

(17)

由式(9)和式(17)可知，x和z方向上的滑动摩擦力分量为：

Ff,x=μkpAPTFEzx,Ff,z=μkpAPTFEzz。

(18)

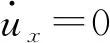
Ff=μkpAPTFEz。

(19)

由式(11),(18)和(19)组成的方程组，即为平面内任意方向上的盆式橡胶支座摩擦数学模型。

2.2 盆式橡胶支座三维有限单元

2.2.1 单自由度体系盆式橡胶支座摩擦数学模型数值求解

对于仅有1个滑动自由度的盆式橡胶支座，其恢复力(即滑动摩擦力)的方向与运动方向相反，起阻碍滑动的作用。应用2.1.2节推导的拓展Bouc-Wen滞回模型计算滑动摩擦力，则单自由度盆式橡胶支座滑动方向上的运动方程为：

(20)

式中，m和c分别为盆式橡胶支座顶板的质量和滑动方向上的阻尼；F(t)为外力。联立式(4)和式(20)，得到下列矩阵形式的微分方程组：

(21)

(1)隐示解法

(22)

式(22)可写为以下形式：

(23)

式中，w是变量u，v和z组成的向量，w=[u,v,z]T；f(w,t)为w关于时间t的函数。式(23)所示形式通常被称为系统的状态空间表达式。

采用Crank-Nicolson有限差分法对式(23)进行离散。时间步长为Δt，任意时刻ti和ti+1间，式(23)可写为：

(24)

将式(24)写为ti+1时刻的求根函数形式，即求解使F(wi+1)=0的wi+1值。

(25)

采用Newton-Raphson法求解式(25)，每个时间步内的求解迭代如式(26)～(28)所示：

Jδw=-F(w-)，

(26)

δw=-F(w-)J-1，

(27)

(28)

式中，w-为每次迭代中函数F(wi+1)的根；J是函数F(wi+1)的雅可比矩阵；δw是w-在每次迭代中的增量。

通过以上方法求解状态空间表达式(23)，即可得到任意时刻盆式橡胶支座顶板的滑动和摩擦状态。

(2)显式解法

目前，桥梁结构振动分析通常使用已成熟的商业有限元软件进行数值计算，此类软件一般预留了用户自定义有限单元接口。将盆式橡胶支座作为一个用户自定义有限单元，在有限元建模中应用，相比于采用上述隐式解法同时求解运动方程和盆式橡胶支座摩擦数学模型，具备更大的适用范围。

在显式解法中，将滞回参数z作为任意时刻t时，方程式(4)的唯一变量。此时方程式(4)由二元一阶微分方程变为一元一阶微分方程。

采用Euler差分法对式(4)进行离散，得到式(29)：

(29)

将式(29)ti+1写为ti+1时刻的求根函数形式，即求解使F(zi+1)=0的zi+1值。

(30)

采用Newton-Raphson法求解式(30)，每个时间步内的求解迭代如式(31)～(33)所示：

F′(z-)δz=-F(z-)，

(31)

(32)

(33)

通过以上方法求解式(4)可得到任意时刻的滞回参数z，再应用常规数值方法求解式(20)所示单元运动方程，得到运动变量，求解过程不再累述。由此即可确定任意时刻盆式橡胶支座顶板任意方向滑动的位移和摩擦状态。

2.2.2 盆式橡胶支座三维有限单元构建

(1)假设和简化

在构建盆式橡胶支座三维有限单元过程中，本研究做出以下假设和简化：

①由于盆式橡胶支座的几何尺寸相较于桥梁结构几何尺寸很小，因此忽略盆式橡胶支座的几何尺寸和形状，仅将支座视为由2个节点连接而成的1个单元。

②忽略盆式橡胶支座钢-聚四氟乙烯界面的不均匀性，假设此界面的材料均匀且各向同性，则支座的摩擦力大小与滑动方向无关。

③忽略支座磨损和支座接触温度变化对摩擦的影响。

④由于在正常使用极限状态下，支座滑动和转动通常较小，因此假设桥梁上部结构压力均匀作用在钢-聚四氟乙烯界面上，忽略支座滑动造成的上部结构偏心压力。

(2)盆式橡胶支座有限单元

盆式橡胶支座三维有限单元由2个节点连接而成，分别模拟盆式橡胶支座的顶板和底板，如图5所示。两节点间相对滑动由盆式橡胶支座摩擦数学模型控制，调节模型参数可约束任意滑动自由度ux和uz，从而模拟单向滑动支座和任意向滑动支座；由于橡胶三向受约束时，抗压强度极大，表现为刚性[17-18]，因此在模型中约束节点间竖向相对位移uy；允许绕滑动平面内两轴转动，即θxy和θyz；约束绕法向轴转动，即θxz。节点间运动约束构成虚拟连接，模型空间中不存在连接实体。

图5 盆式橡胶支座三维有限单元示意图

(3)支座工作中的恢复力与滑动位移关系变化

桥梁结构振动中，盆式橡胶支座滑动界面不断地在滑动和固结状态间变化。同时，对于任意向滑动支座，其滑动方向也受桥梁振动影响而不断改变。支座工作中的恢复力与滑动位移关系发生如下变化。

状态1：界面固结。此状态下，支座没有发生任何宏观滑动位移，处于静摩擦状态。但由于聚四氟乙烯层发生剪切变形，顶板和底板间仍存在微小的相对位移，并随着滑动趋势增大而增大，直至滑动力超过最大静摩擦力Ff,k，如图6(a)所示。

状态2：界面滑动。此状态下，支座开始发生宏观滑动位移，处于动摩擦状态。但由于聚四氟乙烯层发生剪切变形，顶板和底板间仍存在微小的相对位移，并随着滑动趋势增大而增大，直至滑动力超过最大静摩擦力，如图 6(b)所示。

状态3：界面滑动转向。随着桥梁结构振动，支座滑动速度逐渐减小，动摩擦系数随之减小，直至桥梁结构振动达到最大位移，此时支座滑动停止。随着桥梁结构振动转向，支座滑动转向，并在相反方向上重复状态1和状态2。在坐标图上体现为曲线从第1象限进入第3，4象限，并呈现滞回现象，如图6(c)所示。

图6 支座工作中的恢复力与滑动位移关系变化情况

状态4：界面滑动二次转向。随着桥梁结构振动在另一方向上达到最大位移并发生转向，支座滑动再次转向，并在相反方向上重复状态1、状态2和状态3。在坐标图上体现为曲线从第3象限进入第2象限，直至回到第1象限，完成一个完整的滞回环，如图6(d)所示。

3 有限单元工作能力计算验证

设计3组支座摩擦动力工况，应用本研究构建的盆式橡胶支座有限单元进行支座摩擦响应计算分析，验证该有限单元的工作能力。

3.1 任意方向滑动的摩擦响应一致性验证

由于假设钢-聚四氟乙烯界面是均匀且各向同性的，所以任意方向上的滑动摩擦力因具有一致性。当不同方向上滑动速度大小相同时，对应的滑动摩擦力大小也应相同。

(1)工况设置

向顶部节点输入简谐位移波。通过调整位移波在x和z轴上分量振幅大小调整合位移方向，如式(34)所示。简谐位移波输入参数见表2。

表2 简谐位移波输入参数

(34)

(2)支座单元边界条件设置

固定单元底部节点，约束所有滑动和转动自由度；约束单元顶部节点的竖向位移uy和绕法向轴转动θxz允许顶部节点沿x，z坐标轴滑动和绕x，z坐标轴转动。

(3)支座摩擦响应计算结果

计算结果显示，应用本研究构建的盆式橡胶支座三维有限单元计算得到的3个滑动方向(滑动方向与x轴夹角分别为0°，30°和45°)上的滑动摩擦力大小完全一致，如图7所示，其摩擦力-位移滞回曲线完全重合。本研究构建的盆式橡胶支座三维有限单元计算不同方向上的滑动摩擦响应结果符合理论预期。

图7 3个不同方向上的摩擦响应计算值

3.2 滑动方向连续改变条件下的摩擦响应计算能力验证

在实际公路桥梁振动分析中，支座的滑动方向随桥梁振动不断改变，因此盆式橡胶支座三维有限单元应具备计算滑动方向连续改变条件下支座摩擦响应的能力。

(1)工况设置

固定单元底部节点，向顶部节点输入2个坐标轴方向的简谐位移波。调整x和z轴方向位移波的圆频率ω，如式(35)所示：

(35)

如图8所示，输入滑动位移轨迹在滑动平面上呈现“∞”字形。

图8 输入滑动位移轨迹

(2)支座单元边界条件设置

边界条件与3.1中的设置相同。

(3)支座摩擦响应计算结果

如图9所示，x轴方向摩擦力-位移滞回曲线上的点1～5对应图8滑动位移轨迹上的点1～5。由于z方向上的滑动速度始终是x方向上的两倍，在滑动路径1～2上，滑动方向与x轴夹角θ从45°逐渐减小到0，此过程中x轴方向上的摩擦力分量逐渐增大，z轴方向上的摩擦力分量逐渐减小。滑动达到点2时，θ=0，x轴方向上的摩擦力分量达到最大值，z轴方向上的摩擦力分量为0。在滑动路径2～3上，x轴方向上滑动速度减小至0，z轴方向上滑动速度改变方向并逐渐增大，x轴方向上的摩擦力分量减小至0，z轴方向上的摩擦力分量增大至最大值。滑动路径3～5是路径1～3的重复。图9所示计算结果说明，本研究构建的盆式橡胶支座三维有限单元计算滑动方向连续改变条件下的摩擦响应结果符合理论预期。

图9 “∞”字形滑动位移的摩擦响应结果

3.3 计算摩擦响应结果与试验结果对比

(1)工况设置

为验证本研究构建的盆式橡胶支座三维有限单元计算结果的准确性，参考Dolce等[10]，Li等开展的盆式橡胶支座滑动摩擦试验。如表3所示，按上述试验工况输入单元顶部节点位移和单元参数，计算单元摩擦响应。

表3 支座摩擦试验参数

(2)支座单元边界条件设置

边界条件与3.1中的设置相同。

(3)支座摩擦响应计算结果及与试验结果的对比分析

计算结果如图10所示。

图10 试验数值模拟结果

试验1如图10(a)所示，试验结果和数值模拟对比显示，数值模拟得到的滞回曲线与试验结果得到曲线吻合较好。两者最大滑动位移存在一定偏差，原因实际试验中位移控制存在偏差，使试验最大滑动位移略大于设定的位移幅值±50 mm。摩擦力数值计算结果最大误差为9.71%，出现在支座发生固结-滑动状态转变时，随后误差随滑动位移增大而逐渐减小。

试验2，3如图10(b),(c)所示，试验结果和数值模拟对比显示，数值模拟得到的滞回曲线与试验结果得到曲线吻合较好。试验2摩擦力数值计算结果最大误差为35.4%，出现在支座发生固结-滑动状态转变时；进入滑动摩擦阶段后误差较小，最大为9.3%；支座滑动逐渐停止，并再次发生固结-滑动状态转变时，误差明显增大。试验3摩擦力数值计算结果最大误差为48.1%，出现在支座滑动逐渐停止，并再次发生固结-滑动状态转变时；滑动摩擦阶段误差较小，最大为15.6%。

试验结果与数值模拟计算结果对比分析说明，试验参数设置准确时，滑动摩擦阶段的试验结果与数值模拟计算结果误差较小，该有限单元可以较好地模拟桥梁盆式橡胶支座在实际条件下的支座摩擦响应。

4 结论

本研究基于Bouc-Wen滞回模型和以往对钢-聚四氟乙烯界面摩擦机理的研究及相关摩擦试验数据，开发了一种适用于桥梁有限元振动分析的盆式橡胶支座三维有限单元。主要研究工作及结论如下：

(1)对动力条件下盆式橡胶支座的滑动摩擦进行分析，通过拓展Bouc-Wen滞回模型应用范围，结合以往对钢-聚四氟乙烯界面摩擦机理的研究，构建了一套完整描述桥梁盆式橡胶支座任意方向滑动摩擦的数学模型，并给出了该数学模型的显式和隐式数值解法。

(2)基于盆式橡胶支座任意方向滑动摩擦的数学模型及其数值解法，对支座本身及其力学性能适当简化，构建了一种适用于桥梁有限元振动分析的桥梁盆式橡胶支座三维2节点有限单元，该有限单元各项工作性能符合理论预期。

(3)盆式橡胶支座三维有限单元计算结果和以往支座摩擦试验结果吻合较好，说明试验参数设置准确时，该单元能够较好地模拟桥梁盆式橡胶支座在实际条件下的摩擦响应，可以应用于桥梁振动分析中。