基于鬼成像的手写字体分类方法

闫茹钰，王肖霞，习江涛，2，杨风暴，包达尔罕

（1 中北大学 信息与通信工程学院，太原 030051）（2 伍伦贡大学电气计算机与通信工程学院，澳大利亚伍伦贡NSW2522）（3 西安微电子技术研究所，西安 710054）

0 引言

手写字体自动识别作为计算机视觉领域中一种高效的判别方法，可在大幅减少人力的情况下提升字体识别效率，在试卷判别、财务报表等涉及大规模手写字体的自动识别中具有重要的实用价值。实际上，由于个人字体风格迥异、书写习惯不同等常常导致不同手写字体存在较大差异，而不像印刷字体有统一的判别标准。因此，在利用自动识别技术进行字体识别时，常常出现判别效率低甚至失效的问题，严重制约了其实用化进程。

近年来，通常利用机器学习、深度学习等对手写字体的字体特征进行提取与匹配，进而基于分类的思想对字体进行识别。例如：文献［1］针对手写数字在人为判别过程中存在识别效果差的问题，提出一种K-最近邻算法（K-Nearest Neighbor，KNN），用于根据投票法则训练手写数字特征，该方法将未知样本和k个手写相邻样本中所属类别占比较多的归为一类，从而对MNIST数字图像进行分类，由于采用惰性算法，计算简单；文献［2］开发了一种CNN和SVM相结合的混合模型，该方法将CNN作为特征自动提取器，SVM用于二元分类，进而识别MNIST数据集中的数字，由于CNN的感受野易自动提取到最可区分的特征，因此该混合模型有着较高的准确率；文献［3］针对传统机器学习中模型泛化能力差的问题，基于深度神经网络，依据BP算法在训练过程中传递误差值进行权重值和偏置项的值的更新，最终使得输出手写数字的分类结果越来越接近预期值。该类方法虽然一定程度上解决了人工判读所造成的识别效率低、甚至误判的问题，但由于手写字体在提取特征时常常存在边缘、纹理等细节信息的缺失，导致识别中易出现分类结果的错误。此外，在字体识别时均需要对获取的字体图像进行如平滑、去噪等预处理。然而在进行这些处理时易造成图像细节信息丢失，影响识别效率。

鬼成像［4-8］作为一种反直觉间接成像方式，无需事先获取物体的细节信息，可在不直视目标物体的情况下实现对目标物体的快速成像，将其与手写字体自动识别技术相结合，可在不提取特征的前提下，实现对手写字体的识别，有效避免了由于特征细节信息的缺失导致的分类结果不准确或错误的出现。鬼成像在该领域的优势已引起了研究学者的关注，如文献［9-10］分别以MNIST、Fashion数据集为例，将鬼成像与深度神经网络相结合提出了一种不需要提取目标物体特征信息的方法从而提升了识别效率。由于该类方法输入量为一维向量，相比二维图像作为神经网络的输入可以减少对目标物体的探测数量从而缩短训练时间。这为特征细节信息缺失导致的低识别效率提供了有效的解决途径。

同时，基于鬼成像的分类方法输入均为系列桶探测器的值转换成的一维向量。该方法的优势在于：桶探测器的值易探测且探测速度快；以少于手写字体像素值（32×32）的一维向量代替二维图像作为输入时，可简化设计的网络结构，大大降低识别的复杂性；直接利用一维向量对手写字体进行分类识别可跳出识别物体就是识别图像的既存思路，为无成像分类的实现提供可能。然而，这些方法都是基于全连接网络结构所提出的，易导致参数膨胀使得在训练过程中出现过拟合现象，进而直接导致手写字体分类错误。可见，如何避免网络的过拟合现象、提升模型的泛化能力是提升手写字体识别效率的关键。与全连接神经网络相比，卷积神经网络（Convolutional Neural Network，CNN）由于卷积核可参数共享，大大减少网络权重的参数大小，从而有效解决网络在训练过程中的过拟合现象，并且该网络具有更强的自适应性，在识别手写字体时准确率更高。因此，将鬼成像与CNN结合来提升手写字体的识别效率、避免分类错误具有现实意义。

鉴于此，本文将鬼成像原理与CNN结合提出一种解决网络过拟合现象的手写字体自动识别方法。该方法以桶探测器值为输入量，通过数据向量化将残差块［11］加入网络中，利用跳跃连接实现输入的一维向量绕道传输到输出，通过保护输入信息的完整性提高识别效率。

1 结合鬼成像和CNN的手写字体识别

1.1 本文方法

手写字体自动识别方法实现流程如图1所示，其中图1（a）为实现原理流程，图1（b）为实验室开发的探测实验装置。其中，探测系统主要由10uj-5 KHz-532 nm脉冲激光器、像元尺寸为13.67 μm且分辨率为1027×768的数字微镜阵列（Digital Mirror Device，DMD）、频带宽度直流（Direct Current，DC）：DC-11.0 MHz的单像素探测器、光学镜头等组成。DMD作为鬼成像系统的光源调制模块，是产生散斑的核心部件。经DMD调制后产生的光场为哈达玛散斑场。鬼成像作为一种特殊的成像方式，不需要提前知道目标物体的信息，通过照射散斑就可以对目标物体进行成像。而目标物体是被散斑照射的物体，并不是生成的。本文的目标物体是手写图像，选择公开的MNIST、EMNIST数据集。以32×32的手写字体作为被照物体，在全采样时（探测次数为1024次），单像素探测时间约为0.75 s，速度很快并不会对后续的分类识别造成时间上的大量消耗。

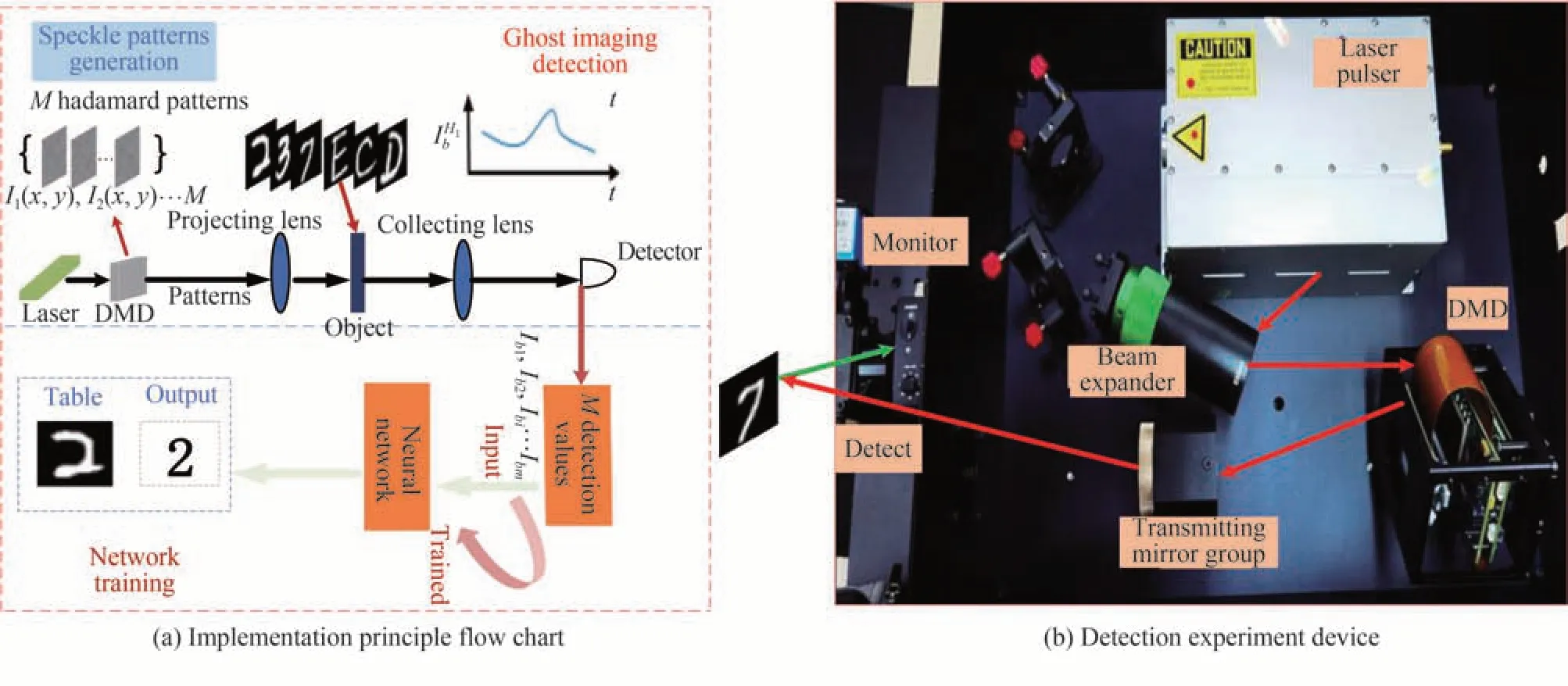
图1 手写字体自动识别方法实现流程Fig.1 The realization process of automatic recognition method of handwritten digit

该方法主要由鬼成像探测和网络训练两部分组成。基本实现过程：利用532 nm的激光器照射像元尺寸为13.67 μm且分辨率为1027×768的DMD设备来产生系列正交的哈达玛（Hadamard）散斑［12-14］，目的是为了减少散斑间的冗余，并利用频带宽度DC-11.0 MHz的单像素探测器来获得物体透射的总光强值。设计的CNN网络由输入层、卷积块、残差块、全连接层、Dropout层和输出层6部分组成。将桶探测器的测量值作为输入并基于CNN网络进行学习，进而给出手写字体的分类结果。具体步骤为：

步骤1：利用532 nm的激光器产生赝热光源，经过DMD调制器来获得不同时刻下照射目标物体且分辨率为32×32的Hadamard散斑图案，即t时刻时Hadamard散斑图案可表示为Ia(x，y：ti)，其中ti为不同的时刻，i=1，2，……M，i表示测量次数。

步骤2：选用公开手写数字数据集MNIST中包含的0～9十类手写数字和公开手写字母数据集EMNIST［15］中包含的字母为被照物体，将生成的系列Hadamard散斑图案分别照射某一手写图像并以桶探测器的值来测量被照物体所透射的总光强值。重复上述过程m次以获得m幅手写图像所对应的桶探测器的值。

步骤3：将探测后的系列桶探测器的值转换为一维向量Ib该一维向量可表示为Ib=[Ib1，Ib2，Ibi……Ibm]，m=1，2，……M。并对转换后的一维向量进行归一化处理，采用最小最大规范的方法（min-max normalization）可表示为

使其映射到0～1范围之内从而加快网络的收敛性。

步骤4：将步骤3获得的一维向量作为CNN网络的输入端进行训练。本方法的卷积神经网络用来连接输入与输出端，其主要由卷积块、残差块、和全连接层3部分组成。

步骤5：利用训练好的CNN分类模型对步骤2中提到的两个数据集中部分手写字体进行测试，最终输出10个神经元对应的10类手写字体。

1.2 基于CNN神经网络架构设计

CNN一般由卷积层、池化层、全连接层构成，可解决全连接网络结构的参数膨胀导致的过拟合问题，并广泛应用于图像分类领域。为解决网络层数增加导致训练时出现梯度消失、梯度爆炸及过拟合现象，将残差块［16］、Dropout层［17］加入其中。

设计的CNN网络模型架构如图2所示，其分类模型由输入层、卷积块、残差块、全连接层、Dropout层和输出层6部分组成。其中，输入部分为长度为M的归一化桶探测器的值；输出为模型预测的手写字体分类结果。连接输入和输出端的中间模块，其主要由卷积块、残差块、全连接层及Dropout层4部分组成。

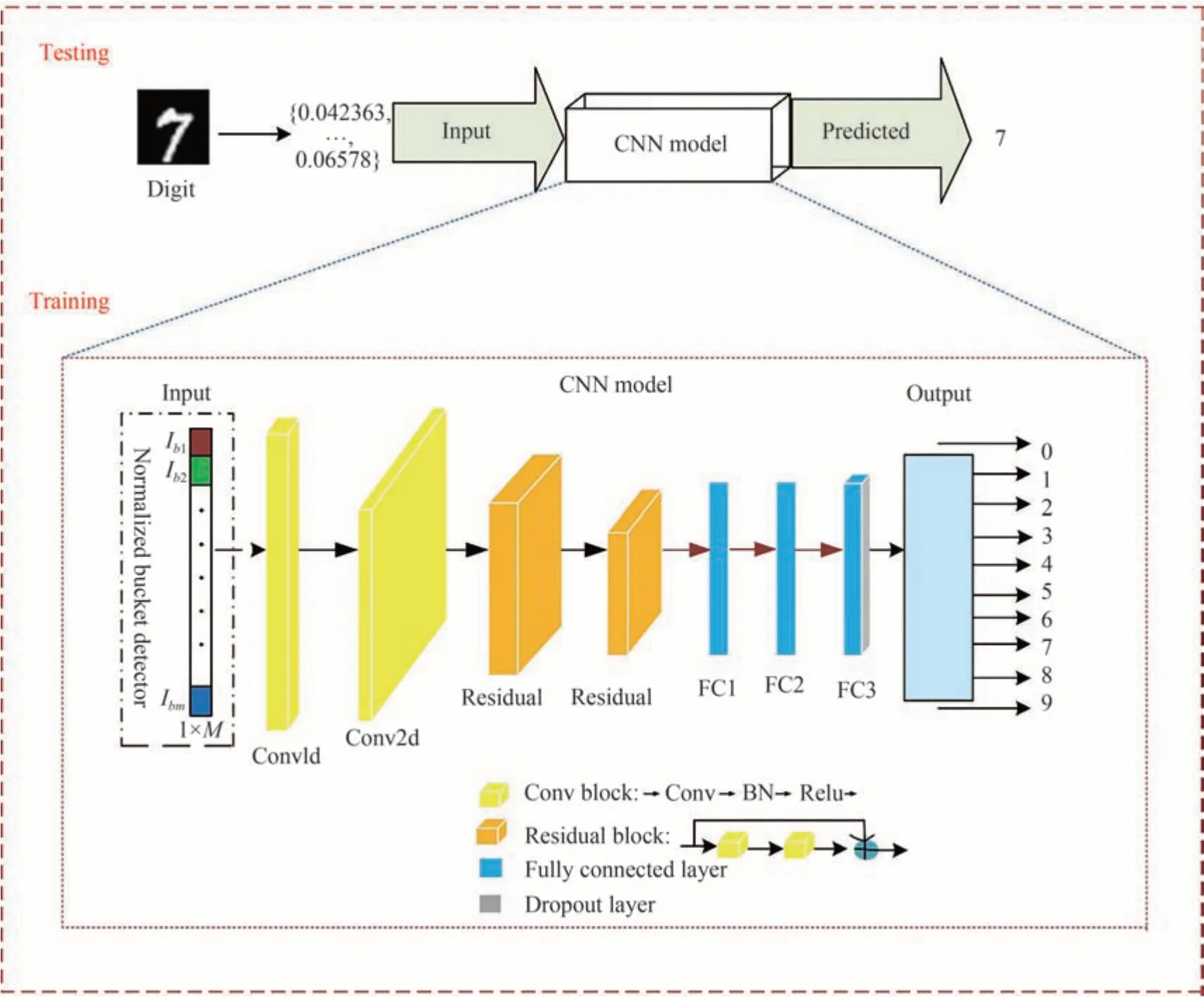
图2 CNN神经网络架构模型Fig.2 CNN neural network architecture model

卷积块由卷积层、批量归一化层（Batch Normalization，BN）［18］和修正线性单元（Rectified Linear，Relu）［19］激活层组成。为了保证卷积前后尺寸不变、padding能够平均分配到卷积张量两边，卷积核的个数一般都设置为奇数，因此，在一维、二维卷积层分别选择卷积核大小为5×5、3×3的滤波器。另外，本文CNN网络架构的输入为系列光强值，为能更好地处理该系列光强值选择一维卷积层。同时，BN层能优化对权重的调整从而加快网络的训练和收敛速度、控制梯度爆炸防止梯度消失。

基于卷积层的残差学习，其中的skip机制可将输入信息由浅层传递到网络的更深层，避免网络层数增加造成大量手写字体信息丢失及梯度消失的问题，也可提高网络的泛化能力从而提升手写字体的识别准确性。

为实现手写字体的多分类任务，在输出部分连接了三层全连接层，作为CNN结构中的多分类器。

Dropout层也可有效防止网络在训练过程中出现的过拟合问题，提高网络的泛化能力。经过多次实验验证，本文选择的Dropout的比例为0.6。

设计的框架使用操作系统为Win10（64位），编程语言python版本3.8（64位），基于PyTorch框架实现了CNN神经网络分类模型。

1.3 数据集准备

鬼成像无需事先获取目标物体的信息，通过散斑照射到目标物体进行成像。被散斑照射的物体就是目标物体。

本文的数据集是从公开的MNIST、EMNIST数据集中分别随机选取其中的17239幅、1442幅手写字体图片经过数据扩充28×28到32×32，然后再经过1.1节的探测方法得到。MNIST是一个公开的手写数字的图片数据集，内容范围为0～9十类手写数字，由60000个训练样本和10000个测试样本组成，每个样本都是一张28×28像素的灰度手写数字图片，且EMNIST为MNIST的扩展数据集，其由26类字母组成。

1.4 评价指标的选取

为了验证和分析所提方法的有效性和合理性，以设计的CNN模型对手写字体部分数据集进行测试。并用准确率A、召回率R、精密度P、F1值作为评价指标，即

根据分类器在测试数据集上预测的正确或不正确可以分为4种情况［20］，其中，真正（True Positive，TP）表示被模型预测为正的正样本的数量；假正（False Positive，FP）表示被模型预测为正的负样本的数量；假负（False Negative，FN）表示被模型预测为负的正样本的数量；真负（True Negative，TN）表示被模型预测为负的负样本的数量。

2 实例验证与结果分析

2.1 基于CNN框架下的实验

实验部分是以图1（b）所给出的鬼成像探测系统来获得测量值。分别从MNIST、EMNIST数据集中随机选取共计17239幅手写字体图像作为该系统中的被照物体，并利用图1（b）探测装置中的DMD生成Hadamard散斑，分别照射目标物体1024次（非欠采样）、256次（欠采样）。为了说明该方法的实用性，分别对非欠采样、欠采样条件下的模型进行训练。由于本文方法采用监督学习，因此，将桶探测器的值及对应的真实手写字体图片作为标签输入到网络中进行训练。

实验结果选取的有效训练周期为100，以交叉熵损失函数来计算实际输出值与真实值之间的误差。计算原理表示为

式中，Loss表示损失函数，参数w、b分别表示各层线性关系中的权重和偏差，x是维数为M的输入一维向量，y对应手写字体的分类输出结果，softmax为输出层的函数，j是神经元的个数。为了对损失函数进行优化，利用自适应矩（Adaptive Moment Estimation，ADAM）优化器［21］，通过使用参数的梯度值对权重和偏置进行更新。同时，学习率作为训练过程中重要的超参数，过小或过大都会对收敛速度和效果造成影响。在经过多次实验后，此模型选择的初始学习率为10-4。

为了验证所构建模型的合理性和有效性，以1442幅手写字体为例分别在全采样和欠采样的情况下将对应的桶探测器的值作为测试集并对训练结束的模型进行验证。

2.2 实验结果及对比分析

本文中的全采样为1024（32×32）次探测，同样地，0.25的采样率代表256（32×32×0.25）次探测。为验证该方法的有效性，以MNIST数据集（随机选取该数据集的12039个训练集，1242个测试集）的0～9十类数字为目标物体进行实验来说明不同采样率下CNN、DNN两种模型准确率分析的结果。图3（a）和（b）分别为采样率1.0、采样率0.25下的0～9每类数字的准确率。

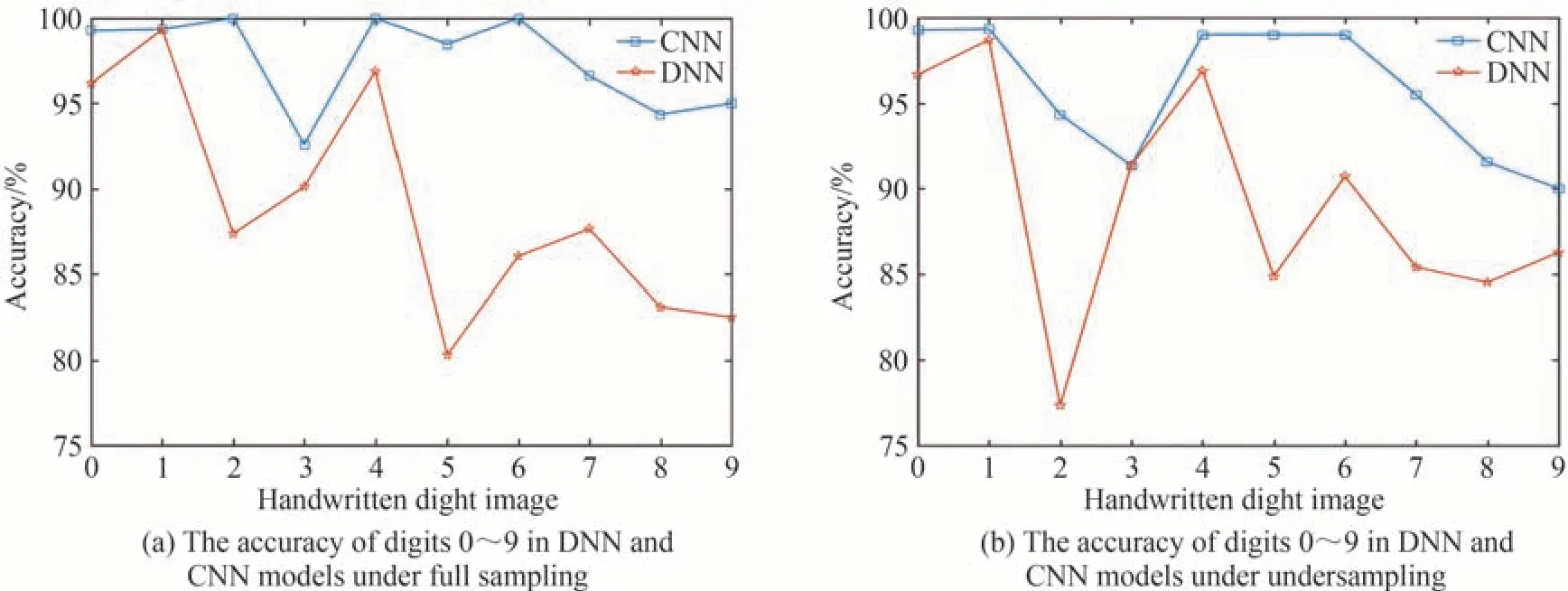
图3 不同采样率CNN、DNN模型下数字0～9的准确率Fig.3 The accuracy of digit from 0 to 9 under different sampling rates of CNN and DNN models

观察图3可知，在相同采样率下，CNN模型对0～9手写数字识别的准确率均高于DNN模型。分别测试了全采样和0.25采样率下DNN、CNN模型中10类数字的准确率，其中全采样时DNN、CNN模型中0～9每类数字的准确率为96.18%/99.28%、99.34%/99.36%、87.36%/99.99%、90.12%/92.59%、96.88%/99.99%、80.30%/98.48%、86.05%/99.98%、87.64%/96.62%、83.10%/94.36%、82.50%/95%；采样率为0.25时两种模型下每类数字的准确率为96.66%/99.28%、98.7%/99.34%、77.36%/94.33%、91.36%/91.35%、96.88%/99%、84.85%/99%、90.70%/99%、85.39%/95.50%、84.51%/91.54%、86.25%/90%。其中，数字2、5、6、7、8、9在全采样和欠采样两种情况下CNN模型比DNN模型有着显著的提升，全采样时分别提升12.63%、18.18%、13.93%、8.98%、11.26%、12.5%；欠采样时分别提升16.97%、14.15%、8.3%、10.11%、7.03%、3.75%。由此可见随着采样率增加识别的准确率也随之提升。因此，定量分析结果与定性分析结果一致。

同时，为了减小实验误差，进一步说明CNN模型在所提方法下的优势，记录了两个模型的最低、最高、平均准确率如表1所示。

表1 基于CNN、DNN模型准确率比较Table 1 Comparison of accuracy based on CNN and DNN models

由表1可见，CNN模型的最低、最高、平均准确率均高于DNN模型下的，且分别提升了8.09%、5.48%、5.31%，验证了CNN模型在该方法下的合理性和有效性。

为了更好地比较两种模型的性能，根据混淆矩阵，在测试部分测试了两种模型的精密度、召回率、F1值，如表2所示。可见，相比DNN模型，CNN模型的精密度、召回率、F1值分别提升了10.75%、11.63%、11.09%，进一步验证了利用桶探测器的值作为网络输入的方法搭建CNN模型的合理性。

表2 DNN、CNN模型下的精密度、召回率、F1值对比分析Table 2 Comparative analysis of precision，recall rate and F1 score under DNN and CNN models

从表2的实验结果可以看出，基于CNN模型的手写数字分类模型具有更好的测试稳定性，表明构建的模型显著提高了分类性能。

为了验证所搭建CNN模型对不同数据集都有一定的学习效果，以EMNIST数据集为例随机选取其中l、v、y、z、m、n、o、r、s、h十类（本文所搭建模型为十分类网络）字母图像作为目标物体分别在采样率为1.0、0.25的情况下对其所对应的桶探测器的值进行训练和测试。采样率1.0/0.25下每类字母对应的准确率的测试结果如图4（a）、（b）所示。CNN模型在不同采样率下的精密度、召回率、F1值如图4（c）、（d）所示。

由图4（a）、（b）可知，全采样和欠采样情况时l、v、y、z、m、n、o、r、s、h十类手写字母在本文提出的CNN分类模型下的准确率分别为90%/60%、90%/85%、100%/70%、90%/60%、95%/95%、70%/75%、85%/90%、95%/85%、100%/70%、85%/80%。除了字母n、o以外，其他字母在全采样时均高于欠采样时的准确率，对比分析说明随着采样率的增加准确率也随之提升。实验结果图4（c）表明在全采样时精密度、召回率、F1值分别为91.87%、90%、90.23%。说明CNN在以字母为目标物体时有较好的分类结果，进一步提高了网络的通用性。

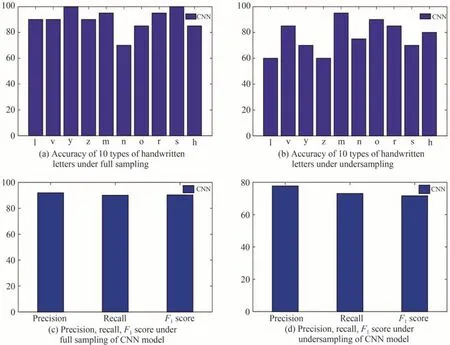
图4 不同采样率下10类字母的准确率及CNN模型精密度、召回率、F1值Fig.4 Accuracy rate of 10 letters under different sampling rates and CNN model precision，recall rate，F1 score

2.4 损失函数分析

研究中发现在统一的损失函数下，CNN比DNN有更强的收敛性。为了说明这一问题，以交叉熵损失函数为例对CNN、DNN模型下的收敛速度进行对比分析，训练误差曲线如图5所示。

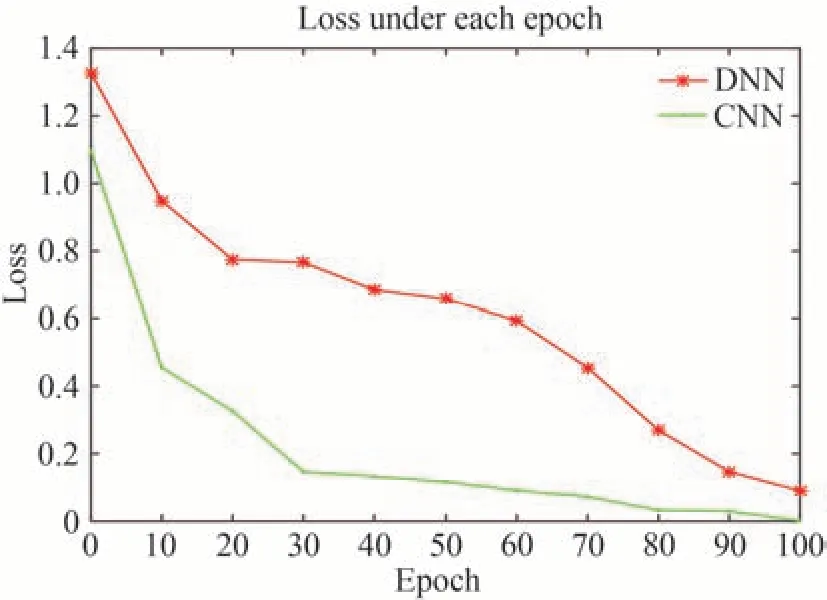
图5不同模型采用交叉熵损失函数下的损失误差曲线Fig.5 The loss error curve of different models using the cross-entropy loss function

图5 表明，训练迭代步数为100时两种模型都可以收敛到一定的误差范围内，CNN的收敛效果明显比DNN的更好，且曲线的收敛速度更快，在训练集训练所获得的损失函数最小值约为0.0014。

3 结论

本文提出一种基于卷积神经网络的鬼成像手写字体分类识别方法，能够解决网络训练中的过拟合问题。与全连接神经网络相比，该方法在低采样率的情况下，仍有着较高的准确率，并且卷积神经网络模型的精密度、召回率、F1值均有明显提高。通过实验，进一步验证了本方法的有效可行性，为提升手写字体识别效率提供了新的解决方案，可推动手写字体识别在实际生活中的应用。在后续的研究中，将进一步优化卷积神经网络结构，使得当目标物体来自其他类型的数据集时仍能达到很好的分类结果。