重传承 显规范 消疑惑
——以“线段的长短比较”为例*
刘清清 黄建福
(安徽省肥西县上派初级中学 231200)
1 问题提出

图1
AD
AD
AB
BD
AD
AC
CD
AD
AB
BD
AD
AC
CD
2 原生态课堂
该教师在讲解线段的比较、线段的和差、线段的倍分时,提出以下几个问题.
问题1 图2中两条线段AB,CD的大小关系怎样表示?
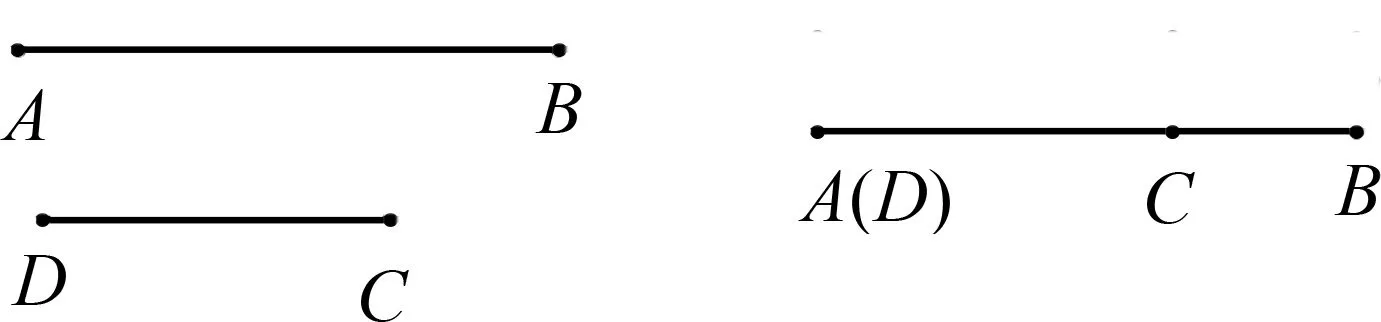
图2 图3
生1:根据叠合法可知AB>CD,或是CD 问题2 图2中叠合后的图形如图3,则图3中有几条线段?它们之间有怎样的数量关系? 生2:共有三条线段,分别是AC,BC,AB.它们三者之间满足AB=AC+BC,AC=AB-BC,BC=AB-AC. 问题3 点C是线段AB上的点,可能会出现一种特殊的位置,你知道是什么吗? 生3:是线段AB的中点. 以下将从两个方面阐述“痴傻”问题产生的客观因素. 本节课看似教师充当着引导者,所有的问题都具有引导性、启发性,但是从知识层面来看,这些问题跨度大、思维深,问题之间衔接不流畅、转折僵硬,没有体现出探究知识的逻辑性与必要性,导致学生出现心理和思想上的巨大分歧. 首先,本节课的难点之一就是要求学生会将图形语言转化成形如AD=AB-BD的几何语言,而在此之前,学生对几何语言知之甚少,甚至对几何语言的认知是空缺的.在“线段的长短比较”之前,学生仅仅学习了点、线段、射线、直线的相关知识,从未涉及用几何语言表示线段的数量关系.因此,突兀地提问“线段的数量关系”已然超出学生理解和认知的范畴.在文[1]中,作者采用了“留白”的方式:先让学生自己解答,列出算式,通过活动学生会发现失去了几何语言的“帮助”,单纯的算式就变得死气沉沉、毫无意义.自然而然,学生会发觉几何语言的必要性.事后,笔者也故意“留白”,让学生大开脑洞,自由选择符号、字母等表示AB,AC,BC三者长度之间的数量关系,学生会给出各种新奇的表示,如AB=AC⊕BC,AB=ACvBC.笔者认为,只要学生能够理解各自选择符号的含义、熟练地使用符号表达图形就是合情合理的.但是,为什么最终选择AB=AC+BC的形式来表示图3的图形语言呢?因为在漫长的数学发展史中,数学家为了研究问题的方便,更是为了传播数学文化知识,统一使用了形如AB=AC+BC的形式来表达图3,这体现了知识的继承性和传承性,对后人快速建立知识体系、继承与发扬数学知识起到了不可替代的作用.而学生具有个人特色的符号仅限于个体理解,不便于他人传阅,这就是为什么最终选用=、+、-等符号来表达AB,AC,BC三者的数量关系.这种表示体现了继承与发展,有着严格的规范性,理应由教师作出示范性的解说,而非是由学生一说了之.教师是数学知识的传播者,亲自解说具有权威性与示范性,更具有说服力,可以减少学生的疑惑与质疑. 除此之外,原生态课堂中教师提出的三个问题跳跃性很大,也是学生产生“痴傻”问题的一个原因.针对问题2,根据学生已有的知识,可以轻易获得图3有三条线段,但是三者的数量关系对学生来说却是质的转变.在问题1中,学生刚刚认知了线段长短比较的简记方法,但是问题2中,由两条线段飞跃成三条线段,由不等的数量关系生成相等的数量关系,不能生硬地、人为地“生成”,更不能由学生的回答草草收场,还需要巧妙的过渡与引导,问题3就是典型的人为(教师)“诱导”.从数学知识的逻辑性来看,问题1、问题2、问题3之间缺乏关联,存在着逻辑的断层,教师亦不能对这种断层给出合情合理的讲解,仅仅用学生的回答匆忙结束,难免让学生心生疑窦. 以上简述了学生“痴傻”问题产生的原因,据此,在课堂上试图让学生与教师达到思想共鸣,这需要在原有的教学理念下“修复”原生态课堂,对接学生思想,让课堂问题做到最大限度的合情合理、自然连贯. 问题① 请用叠合法比较图2中线段的长短.哪条线段的长度较长,哪条线段的长度较短? 生4:根据叠合法可知,线段AB的长度比较长,线段CD的长度比较短. 师:像线段AB和CD长度的长短关系,我们可以用AB>CD表示,它既表示线段AB与线段CD的长度比较的结果,又可以表示线段的长短关系.你还能写出类似的式子吗? 生5:CD 师:在问题1中,两条线段叠合的图形如图3,请你观察,图中有几条线段? 生6:共有三条线段,分别是线段AB、线段AC和线段BC. 问题② 线段AB比线段AC长了多少? 生7:根据叠合法可知,线段AB比线段AC长了线段BC. 师:我们可以用BC=AB-AC表示这种图形语言.你可以写出类似的式子吗? 生8:AC=AB-BC,AB=AC+BC. 问题③ 在图3中,若点C是线段AB上的动点,点C从点A向点B运动的过程中,线段AC,BC,AB三者的数量关系如何?线段AC与线段BC的大小关系又发生怎样的变化? 生9:无论点C如何运动,线段AC,BC,AB始终满足AB=AC+BC,AC=AB-BC,BC=AB-AC.但是线段AC与线段BC的大小关系随着点C的运动而变化,先是AC>BC,接着AC=BC,最后AC 师:点C在线段AB上自左向右运动的过程中,出现了AC>BC,AC=BC和AC 生(众):AC=BC. 师:像这样的点C叫做线段AB的中点.请你用自己的语言尝试描述中点的定义. 在讲解“AB>CD”时,再生态课堂采用的问题是“哪条线段的长度较长,哪条线段的长度较短”,替代了“两条线段AB,CD大小关系怎样表示”,注重了学生的认知基础.在此问题的回答中,再生态课堂是教师首先示范了“线段AB比线段CD长”用“AB>CD”表示,再明晰AB>CD表示的两种含义:既表示线段长度比较的结果,又可以表示线段的长短关系.这里,不是借助学生的回答告知全体学生,而是教师本人直接讲授.学生可能会回答出“AB>CD”,但是对其蕴含的两种含义不能深入地领悟,这种深层次的理解与表达需要教师的讲解. 学生在初学线段的和差关系时,仅仅知道线段AB,AC,BC三者长度之间的数量关系,但是不知道如何用式子表示.在课堂上,我们不排除有学生会想到用“AB=AC+BC”的形式表示,但是这只是一部分学生,并不能代表全部的学生均认可这种表示方法.若是在初学时,教师没有示范和规范图3的几何语言,就会导致学生心理上认同而思想上质疑的现象.因此在再生态课堂中,教师提问“线段AB比线段AC长了多少”,替换了原生态的问题2(它们之间有怎样的数量关系?),将几何语言揉碎成学生能够理解的文字语句,接着教师再规范板书“线段AB比线段AC长了线段BC”可以用式子“BC=AB-AC”表示.教师在此处讲授的作用不仅仅是强调式子的规范性,更是用学生的认知语言解释了式子的书写,达到了获取新知与学生认知的统一. 原生态的课堂中,问题3的提出略显生硬和刻意,线段上特殊位置或特殊点繁多,而本节课为什么要研究中点,中点的存在性和唯一性没有解释透彻,学生完美无瑕的回答是对教师违心地“迎合”.将问题3改换成问题③,利用“线段AC与线段BC的大小关系”让中点的存在性和唯一性曝光在点C的运动过程中,通过运动的观点解释了中点的客观性、特殊性和学习的必要性. 在教学中,我们时常会遇到与学生不能达到感情与思想共鸣的情况,教师认为显而易见的问题,是容易理解或不需要解释的内容,偏偏学生就是不理解、不能领悟.这时,我们当以初学者的眼光阅读课本,去发现问题的根源.翻阅课本时便会发现,“线段的长短比较”一节中有一个词因反复出现而显得特别醒目.课本在讲解线段的长短比较时是这样描述的:当点D在线段AB内部时,线段AB大于线段CD,记作AB>CD;在讲解线段的和差时,表述如下:点D在线段AB上,那么线段AD就是AB与BD的差,记作AD=AB-BD[2].诸如此类的表述还有很多,这里“记作”二字意味着“约定俗成”,类似于“三角形ABC”可以记作“△ABC”.因此此处应该由教师规范书写,阐述知识的传承性与统一性,不能由学生替代教师的示范作用,以免引发不必要的误会,从而引发学生产生“痴傻”问题. 透过“原生态问题解决”环节,可以探知“痴傻”问题产生的客观原因,因为教学过程中,教学问题跨度大、台阶高,教师过高地预估了学生的认知,过多依赖于看似能够自主学习的学生,没有正确认知教师的主导地位.在再生态课堂中,教师充分研读学情,准确评价学生的学情(问题①),作出正确示范(问题②),将本节课的难点转化为学生易于理解的方式表达(问题③),探索了学习知识的必要性和特殊性(问题③),从而引导认知与获取的和谐,避免学生产生思想质疑与心理认同的不协调,防止痴傻问题的产生. 数学知识的学习过程其实就是学生继承先人遗志并发扬光大,而先人遗志的播撒者就是教师.因此,我们倡导学生主体性并非是“一刀切”和盲目的,当遇到需要教师作出规范性讲解时,不能由学生代劳.教师应该将知识掰开了、揉碎了,使用学生的认知语言将知识讲解透彻,才能尽可能减少“痴傻”问题的提出.因为继承与发展对学生来说,不是一时的热情,而是持久的恒温,“痴傻”问题的背后是对约定俗成的未知以及教师规范性讲解的欠缺,恰恰这份“痴傻”是学生继续探究知识的不竭动力和永久“保鲜剂”.3 “痴傻”现象剖析
3.1 知识认知层面
3.2 课堂问题层面
4 再生态课堂
5 原生态问题解决
5.1 再生问题1
5.2 再生问题2
5.3 再生问题3
6 教学反思
6.1 对原生态的反思
6.2 对再生态的反思

