雨水入渗条件下地基瞬态极限承载力解析解及其应用

徐瑞麟，秦卫星,3，胡惠仁，刘泽辰，熊轩宇

(1.长沙理工大学 国际工学院，湖南 长沙，410114；2.长沙理工大学 水利与环境工程学院，湖南 长沙，410114；3.水沙科学与水灾害防治湖南省重点实验室，湖南 长沙，410114；4.长沙理工大学 交通运输工程学院，湖南 长沙，410114)

基质吸力对地基承载性能有较大影响，合理考虑基质吸力贡献，能有效挖掘非饱和地基承载潜能，确保工程设计安全，节约建设成本[1-6]。然而，在施工过程中，裸露地基经常遭遇降雨，雨水入渗会导致地基中上部土体基质吸力减小，进而引起地基承载性能降低，给工程安全造成不利影响[7-11]，因此，准确预测雨水入渗影响下地基基质吸力变化过程，揭示地基极限承载力演化规律，对正确评价雨季地基承载性能、及时采取针对性措施防止施工期地基失稳破坏具有重大现实意义。研究雨水入渗影响下地基基质吸力演化特性以及基质吸力对地基承载性能的影响，一直是非饱和地基领域的研究热点。SRIVASTAVA 等[7]基于Richards一维非饱和渗流方程，研究了降雨过程中土体基质吸力演化规律，获得了均质和双层土体的瞬态渗流解析解。吴礼舟等[8]推导了单层和双层土体渗流与变形耦合的基质吸力解析解，分析了雨强与土体参数变化对基质吸力分布的影响。胡惠仁等[11]探究了降雨条件下均质黏土地基基质吸力演化规律，并基于正交试验方法分析了土体水力参数和降雨特征参数影响基质吸力的显著性。VANAPALLI 等[2-3]通过室内试验研究了基质吸力对非饱和砂土地基极限承载力的影响，试验结果表明基质吸力为2～6 kPa区间的地基极限承载力为饱和时的5～7倍。李艳等[4]通过理论分析发现地基承载力在低基质吸力范围内随基质吸力增大而快速呈线性增加，在高基质吸力范围内随基质吸力增大而呈非线性缓慢降低，并逐渐趋于稳定。赵炼恒等[12]根据Fredlund非饱和抗剪强度理论提出了基质吸力沿深度均匀分布和沿深度线性减小时的非饱和地基极限承载力计算方法。VAHEDIFARD等[13]推导了稳定渗流情况下非饱和土浅基极限承载力计算公式，对比了不同降雨强度雨水稳定入渗情况下砂土、淤泥质土以及黏土地基的极限承载力。谢研[14]采用有限元分析方法研究了降雨条件下地基基质吸力演变特性，并利用可靠度分析理论进一步探究了地基极限承载力变化规律。张常光等[15]基于平面应变条件下非饱和土的抗剪强度统一解，推导了不同基质吸力分布时条形地基太沙基极限承载力公式。上述研究成果表明雨水入渗对黏土、砂土等各种地基极限承载力均有显著影响，采用的研究手段为进一步深入研究和评价非饱和地基承载性能提供了有益借鉴，但当前研究多假定基质吸力为线性分布，这与实际雨水入渗过程的基质吸力非线性分布存在较大差异，也未能直接揭示雨水非稳定入渗过程中非饱和地基承载性能演化规律，影响了对雨季地基承载性能的快速、准确评价。为此，本文作者以非饱和均质地基为研究对象，针对恒定雨强非稳定入渗情况下地基基质吸力和承载性能演化规律问题进行研究。首先，基于Richards 瞬态非饱和渗流方程，引入Gardner 土-水特征曲线模型，获得雨水入渗过程均质地基瞬态基质吸力解析解，并利用有限元模拟结果进行了考证。然后，基于非饱和土抗剪强度理论，推导基质吸力沿深度非线性分布时的地基极限承载力表达式，并利用试验数据证明其正确性。最后，以某非饱和均质地基为例，根据建立的地基基质吸力解析解和极限承载力计算公式，揭示恒定雨强非稳定入渗影响下均质地基基质吸力和极限承载力演化规律。

1 降雨条件下地基基质吸力与极限承载力表达式

1.1 雨水入渗过程地基基质吸力求解

1.1.1 基本假定

进行如下假定：1) 地基土体均质且各向同性，雨水入渗过程土体孔隙保持不变；2) 雨水入渗过程地下水位保持不变；3) 地基遭遇降雨强度不大于土体饱和渗透系数的均匀型降雨(降雨强度与渗透系数的量纲相同)，雨水以恒定降雨强度入渗[7-8]。基于上述假定，绘制雨水入渗作用下地基基质吸力计算示意图，如图1所示。

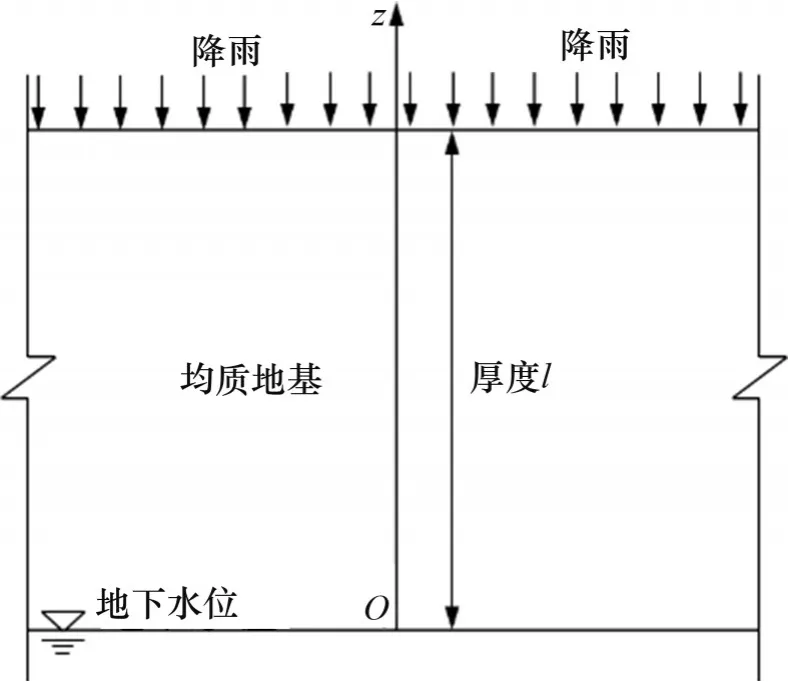
图1 地基基质吸力计算示意图Fig.1 Schematic diagram of calculation of matric suction for foundation

1.1.2 控制方程及方程化简

由Richards瞬态非饱和渗流方程，结合上述假定条件可得混合格式的地基渗流控制方程：

式中：k为非饱和土体渗透系数，cm/h；z为研究点相对地下水位对应深度，cm；hm为z处基质吸力水头，cm；θ为体积含水量，cm3/cm3；t为时间，h。

为解决非饱和土渗透系数与基质吸力高度非线性关系给式(1)求解造成的困难，采用GARDNER 等[16]提出的渗透系数函数和土-水特征曲线模型来描述地基渗透系数k、体积含水量θ与基质吸力水头hm的关系：

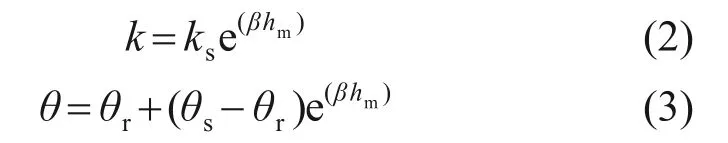
式中：ks为饱和渗透系数，cm/h；β为去饱和系数，cm-1；θr为残余体积含水量，cm3/cm3；θs为饱和体积含水量，cm3/cm3。

由式(2)可知hm=(lnk-lnks)/β，将其代入式(1)，化简后可得

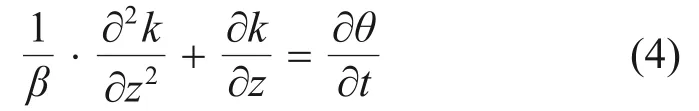
由式(2)和(3)可知θ=θr+k(θs-θr)/ks，将其代入式(4)，整理后可得

1.1.3 初始条件及边界条件

地基初始基质吸力状态对雨水入渗过程基质吸力大小及其分布有重要影响。国内外研究者常以较小的前期降雨强度qA稳定入渗形成的基质吸力分布状态作为初始条件[7-8,17]。本文采用该方法得到地下水位埋深小于10 m 的均质地基初始基质吸力分布：

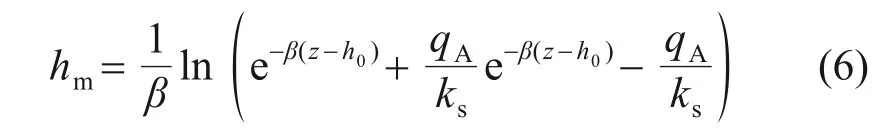
式中：h0为地下水位处的基质吸力水头，通常h0取0 cm。

式(6)直观反映了土体特性、地下水位以及雨水稳定入渗强度等内外部因素对地基基质吸力的影响。当前期降雨强度qA=0 cm/h时，地基基质吸力水头hm沿深度方向呈线性分布；当qA≠0 cm/h时，地基基质吸力水头hm沿深度呈现明显的非线性分布特征。

根据前面基本假定，计算模型的边界条件设定为地下水位处基质吸力hm恒为h0，地表处入渗流量为后期降雨强度qB。

1.1.4 基质吸力解析解

参照文献[7]的处理方法，将式(5)、初始条件与边界条件化简，再通过拉普拉斯变换得到土体瞬态非饱和渗透系数[18]，代入式(2)可求得任意时刻非饱和地基基质吸力水头解析解：

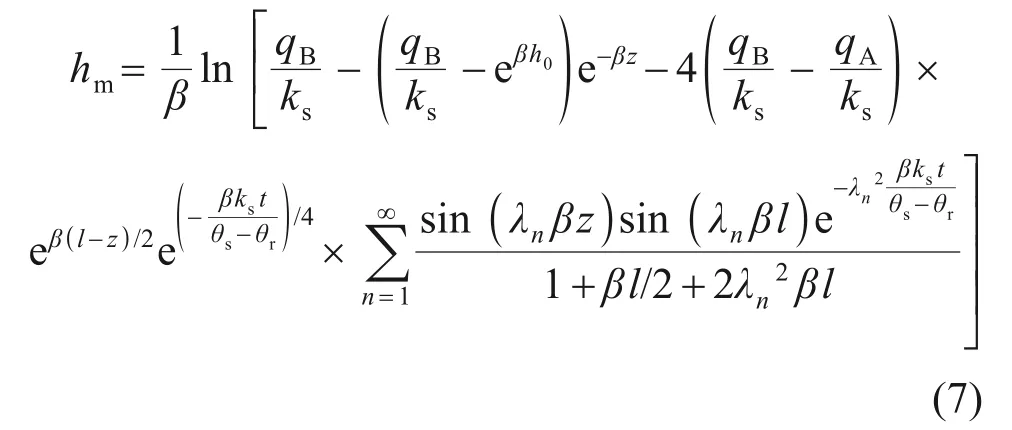
式中：λn为方程tan(λβl)+2λ=0 的第n个根，可编制MATLAB 计算程序求解。为便于后文计算地基极限承载力，将式(7)中基质吸力水头转化为压力形式表示：

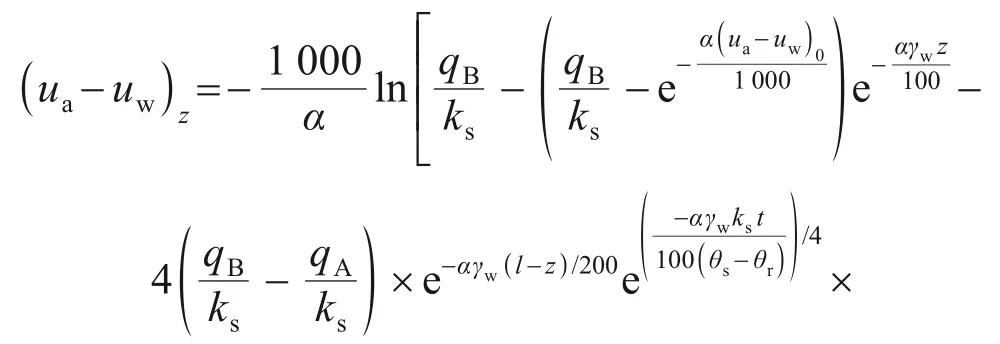
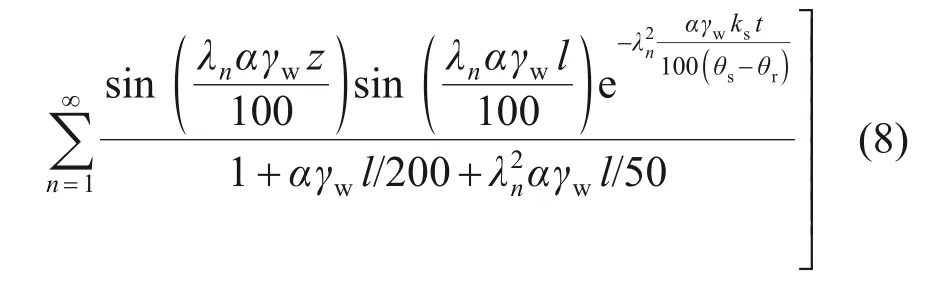
式中：α为与去饱和系数β相关的参数，α=100β/γw；γw为水的重度。

1.1.5 解析解考证

某非饱和均质地基地下水位距离地表5 m，降雨过程保持不变，土体物理力学参数如下：饱和渗透系数ks为0.36 cm/h，去饱和系数β为0.001 65 cm-1，进气值(ua-uw)a为26.32 kPa，储水量(θs-θr)为0.27 cm3/cm，残余含水量θr为0.20 cm3/cm，重度γ为20 kN/m，有效黏聚力c′为18 kPa，有效内摩擦角φ′为16°。假设地基分别遭遇无前期降雨和较小降雨2种初始状态，即qA分别为0 cm/h和0.1 cm/h。后期遭遇降雨持续24 h、总雨量为72 mm 的大雨，可知后期平均降雨强度qB为0.3 cm/h。

取长为10 m、高为5 m范围内的地基为研究对象，建立如图2所示的均质地基雨水入渗分析有限元数值模型。分别利用Geo-Studio软件的渗流有限元计算模块SEEP/W 和式(8)所示基质吸力解析解，计算降雨过程地基基质吸力，对比二者计算结果，即可验证非饱和地基基质吸力解析解的正确性。

图2 降雨入渗有限元数值模型Fig.2 Finite element numerical model under rainfall infiltration

整个降雨过程非饱和地基基质吸力的演化规律如图3所示，图中点对应数值模拟结果，线对应解析解。从图3可以看出2种方法获得的雨水入渗作用下地基基质吸力大小及其变化规律几乎一致：前期无降雨发生时初始基质吸力沿地基深度呈线性分布，但前期有降雨发生时初始基质吸力沿地基深度呈非线性分布；在遭遇同样降雨强度和雨量的后期降雨入渗后，前期有降雨发生时地基沿深度的基质吸力明显比无降雨发生时的小，充分体现了基质吸力初始状态对最终状态的影响；无论地基是否遭遇前期降雨入渗，降雨过程中地基上部土体基质吸力均随时间推移不断减小，基质吸力受影响深度持续增加，基质吸力沿深度演化呈现明显非线性特点。因此，本文推出的非饱和地基基质吸力解析解可实时反映雨水入渗过程地基基质吸力分布状况，为非饱和地基极限承载力计算提供了支持。

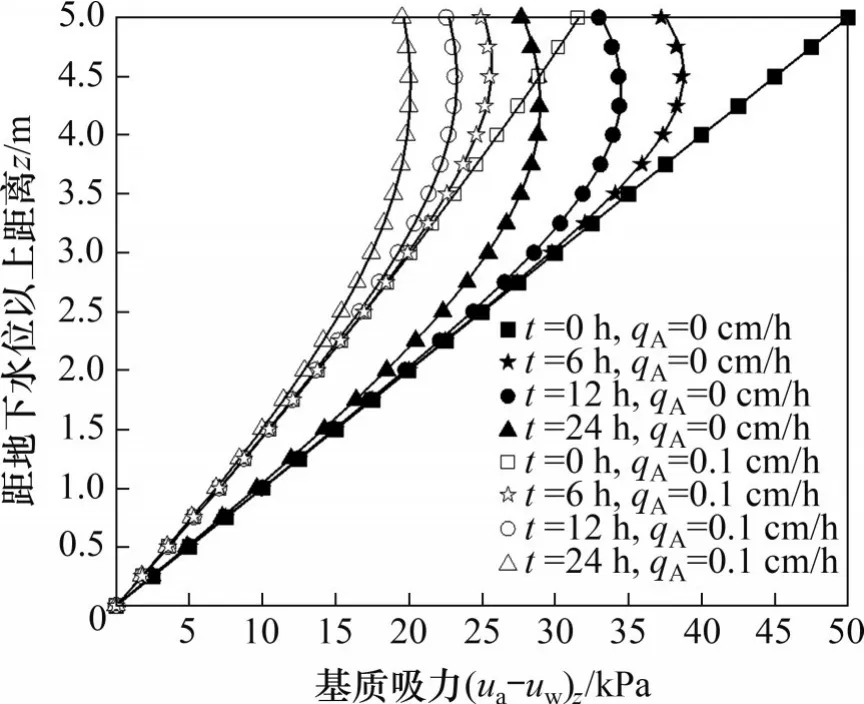
图3 不同前期降雨强度qA下地基基质吸力演化对比Fig.3 Comparison of evolution of matric suction for foundation under different previous rainfall conditions

1.2 非饱和土地基极限承载力计算

1.2.1 非饱和土地基极限承载力表达式推导

对于非饱和地基极限承载力，应合理考虑基质吸力的影响。国内外学者通常基于Bishop 非饱和土抗剪强度理论，采用下列方法考虑基质吸力对地基极限承载力的贡献[2-3,15]。

1) 基质吸力产生的吸附强度与一般黏聚力的性质相似，可由下式计算：

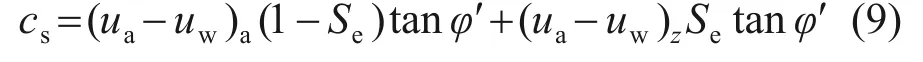
式中：Se为有效饱和度，Se=(θ-θr)/(θs-θr)。

2) 在非饱和地基极限承载力计算中，将吸附强度cs与土体有效黏聚力c之和作为总黏聚力来考虑基质吸力的贡献。根据经典太沙基地基极限承载力计算理论，可得基质吸力沿深度均匀分布时宽为b、埋深为d的基础，非饱和地基极限承载力计算公式为

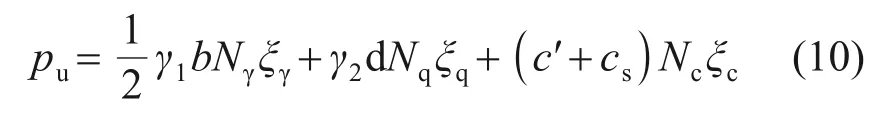
式中：γ1为基底以下土体重度，kN·m-3；γ2为基底以上土体重度，kN·m-3；Nγ，Nq和Nc分别为重度、荷载、黏聚力对应的承载力系数；ξγ，ξq和ξc分别为重度、荷载、黏聚力对应的形状系数，其求解方法和过程可参照文献[3]。

由于降雨条件下地基基质吸力呈现明显非线性分布特征，式(10)不能直接用于计算雨水入渗时地基的极限承载力。POULOS 等[19]通过研究指出上部荷载传递到地基时，对地基应力的影响范围集中在基底以下1.5倍基础宽度的球形区域。基于此研究成果，文献[2]和文献[13]分别在地基承载性能的试验和理论研究中将基底下应力球内平均基质吸力用于地基极限承载力计算，较好解决了基质吸力沿深度非线性分布时地基承载性能分析与评价问题。因此，本文采用该方法来分析和计算降雨条件下地基基质吸力非线性分布时地基极限承载力。以基础中心线与地下水位线交点为坐标原点，z轴铅直向上，x轴水平向右，建立如图4所示的坐标系。降雨任意时刻基质吸力的分布函数可通过式(8)转化为函数x=f(z)表示。如图4 所示，在基底以下1.5 倍基础宽度b范围内画应力球，该应力球范围内基质吸力分布曲线与坐标轴z围成图形形心O处的基质吸力即为该时刻平均基质吸力。图中所示阴影部分形心O的纵坐标zO可由下式计算：

图4 非饱和地基平均基质吸力确定Fig.4 Determination of average matric suction in unsaturated foundation

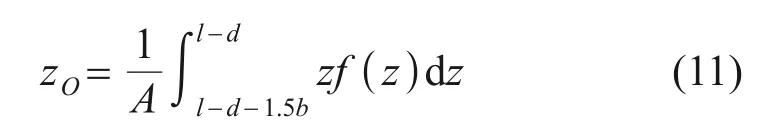
式中：A为阴影部分面积。

将式(11)代入式(8)得到平均基质吸力(ua-uw)zO，结合式(3)所示土水特征曲线模型，得到降雨过程非饱和地基极限承载力计算公式：

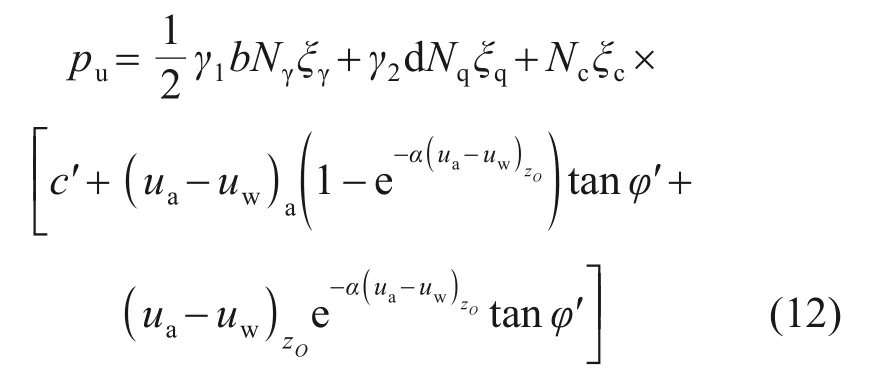
式(12)反映了极限承载力与地基土体物理力学参数、基础形状和尺寸、降雨强度和降雨历时、地下水位位置之间的映射关系，反映了沿深度非线性分布基质吸力对地基极限承载力的影响。当平均基质吸力(ua-uw)zO为0 kPa时，式(12)退化为传统饱和抗剪强度理论下的太沙基地基极限承载力计算公式。

1.2.2 解析解考证

VANAPALLI 等[2]开展了非饱和粗粒砂性土地基极限承载力模型试验。试验模型槽长×宽×高为900 mm×900 mm×750 mm。土体参数如下：重度γ为19 kN/m3，有效黏聚力c′为0.6 kPa，有效内摩擦角φ′为39°，β为0.131 4 cm-1，进气值(ua-uw)a为5.68 kPa。试验中采用埋深d为0 mm、宽b为100 mm、长f为100 mm 的矩形基础，测试得到基质吸力为0，2，4 和6 kPa 时对应的实际基础承载力分别为121，570，715和840 kPa。

采用式(12)计算基质吸力在0～30 kPa范围内的地基承载力，与文献[2]测试的地基极限承载力试验结果进行对比，结果如图5 所示。由图5 可知：当基质吸力为0，2，4和6 kPa时，据式(12)计算的地基承载力与试验结果非常接近，两者的归一化均方根误差为7.8%，低于10%，表明式(11)的地基承载力计算结果准确率高[20]。从图5 还可以发现：基质吸力对地基极限承载力影响显著，基质吸力位于2～6 kPa区间的地基极限承载力为饱和时极限承载力的5～7倍；当基质吸力较小时，地基承载力与基质吸力随基质吸力增大几乎呈线性关系快速增大；当基质较大时，地基承载力随基质吸力增加先非线性缓慢减小，然后趋于稳定，这一规律与文献[2-4]的研究结论一致。综上所述，本文推导的地基极限承载力计算表达式(12)可反映降雨导致的基质吸力改变对地基极限承载力的影响，为快速获取降雨入渗过程地基实时极限承载力提供了一种简便方法。

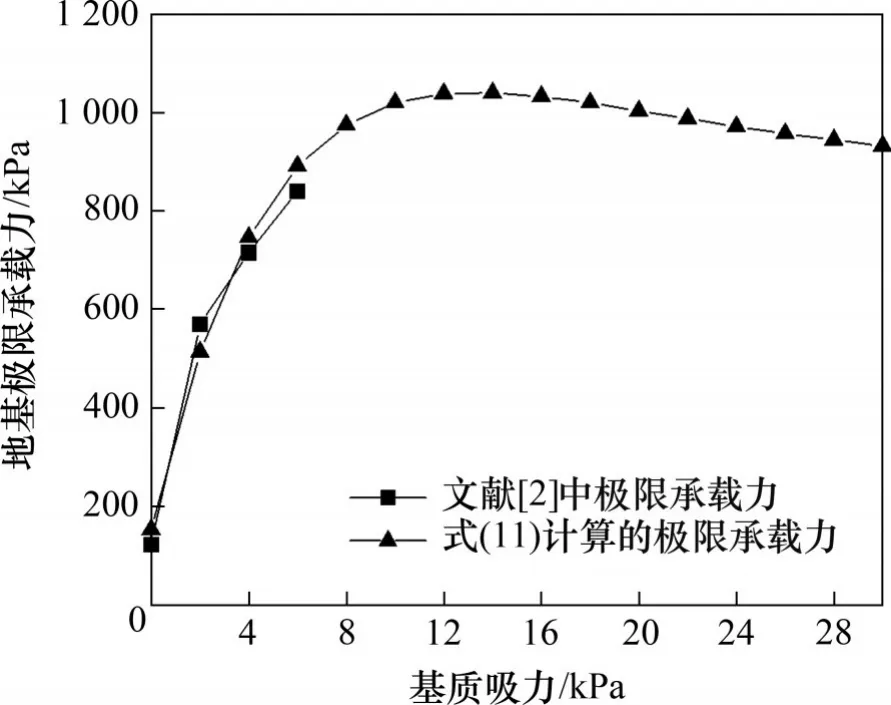
图5 地基极限承载力对比Fig.5 Comparison of ultimate bearing capacities for foundation

2 降雨过程地基承载性能演化分析

2.1 计算模型及计算条件

以1.1.5节采用的非饱和均质地基为研究对象，计算示意图见图4。条形基础宽b为1 m，长f为10 m，埋深d为0 m，基底完全粗糙。地表距地下水的高度l为5 m，应力球沿深度范围为[0，1.5b]。前期降雨强度qA为0 cm/h，初始时刻基质吸力沿深度线性分布。在后期降雨过程中，地下水位保持不变，直接以降雨强度qB作用在地基表面。通过计算不同降雨历时、降雨强度组合方案下地基基质吸力和极限承载力，揭示雨水入渗过程地基基质吸力和极限承载力的演化规律。

2.2 降雨历时对地基极限承载力的影响

为探究降雨过程地基基质吸力和承载力的演化规律，选取降雨强度qB=0.36 cm/h的暴雨，对比分析降雨历时0，12，24，48，96，168，240 和360 h 的地基基质吸力和极限承载力。在降雨过程中，地基基质吸力沿深度演化过程如图6所示，基底以下1.5倍基础宽应力球范围内平均基质吸力以及饱和与非饱和地基极限承载力演变过程如图7所示。由图6和图7可知：

图6 降雨过程中地基基质吸力沿深度演化过程Fig.6 Evolution of matric suction along depth for foundation during rainfall

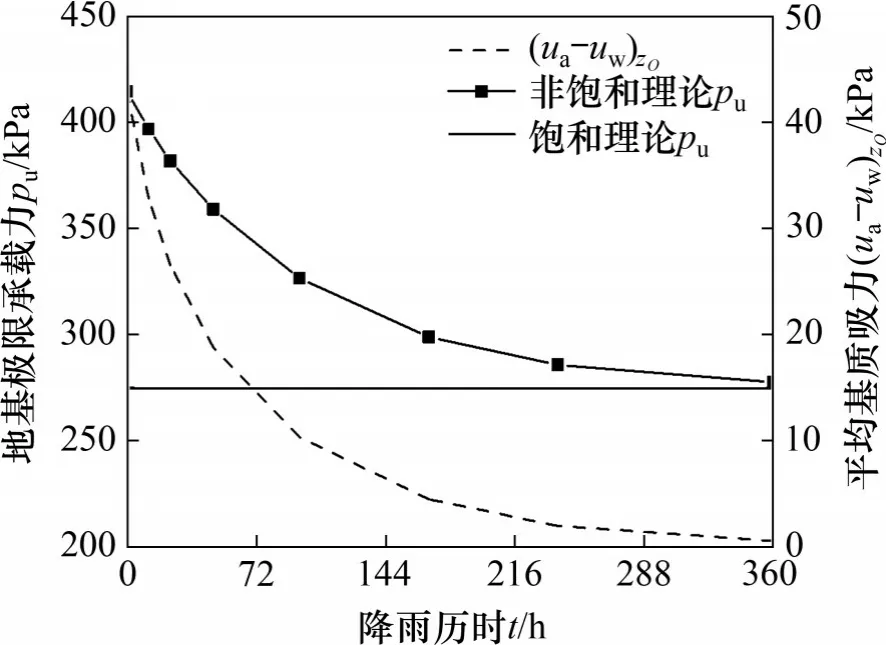
图7 降雨过程中地基平均基质吸力和极限承载力演化Fig.7 Evolution of average matric suction and ultimate bearing capacity for foundation during rainfall

1) 随着雨水入渗，地基基质吸力沿深度快速呈现非线性分布特征，中上部土体基质吸力不断减小，地表处基质吸力从初始的50 kPa降低至15 d后的0.5 kPa；基质吸力受影响深度持续增加，下渗雨水历时2 d左右到达地下水位附近。地基应力球内的平均基质吸力随雨水入渗呈现先快后慢的减小趋势，雨水入渗2 d 后平均基质吸力下降42%，15 d后基底应力球范围内土体逐渐饱和，平均基质吸力最终将降为零。

2) 降雨入渗前非饱和地基极限承载力为414.6 kPa，约为饱和地基极限承载力的1.5 倍。随着雨水入渗，地基极限承载力随基质吸力减小而降低。雨水入渗15 d 后，基底应力球范围内平均基质吸力将逐渐降为零，地基极限承载力最终降至饱和抗剪强度理论计算的极限承载力274.5 kPa。地基极限承载力降低趋势随降雨历时整体呈现先快后慢的特点，因此，应重点加强降雨初期基底基质吸力和承载性能的监测预报，防止降雨过程中地基承载力快速下降诱发工程灾害。

2.3 降雨强度对地基极限承载力的影响

分别选取0，0.04，0.10，0.20，0.30和0.36 cm/h共6种降雨强度作为后期降雨强度qB，用于分析地基基质吸力和极限承载力的演化规律。经过5 d雨水入渗后，各种降雨强度对应的地基基质吸力沿深度分布如图8所示，基底应力球范围内平均基质吸力以及饱和与非饱和地基极限承载力对比如图9所示。

图8 不同降雨强度下入渗5 d的基质吸力沿深度分布对比Fig.8 Comparison of matric suction distribution along depth at different rainfall intensity infiltrations after 5 d

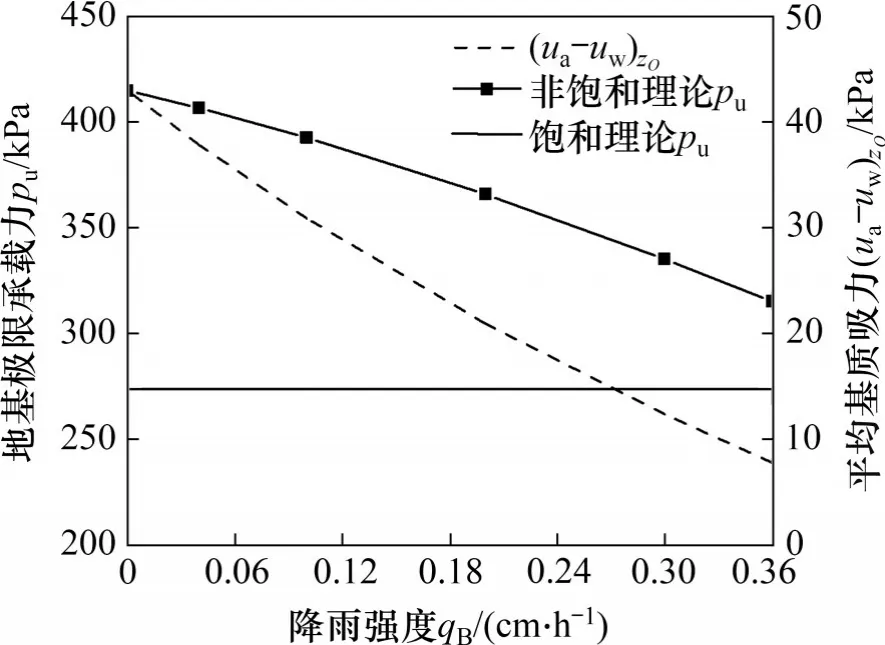
图9 不同降雨强度下入渗5 d的平均基质吸力和极限承载力对比Fig.9 Comparison of average matric suction and ultimate bearing capacity at different rainfall intensity infiltrations after 5 d

由图8和图9可知：

1) 各种降雨强度的雨水入渗5 d后，地基中上部土体基质吸力均呈现非线性分布特点。基质吸力减少幅值、受影响深度随着雨强增大而增加，且上部基质吸力降低幅度大于下部区域的降低幅度，在6 种不同的后期降雨强度(0，0.04，0.10，0.20，0.30 和0.36 cm/h)下地表处基质吸力的减小幅值分别为6.6，15.3，27.3，37.8 和43.1 kPa。基底应力球范围内平均基质吸力随降雨强度增加几乎呈线性下降，从最初的42.9 kPa 减小至qB=0.36 cm/h 时的7.8 kPa。

2) 在不同降雨强度入渗5 d后，地基极限承载力随雨强度增加几乎呈线性下降趋势。当降雨历时相同时，降雨强度越大，入渗地基的雨水越多，基质吸力减小幅度越大，地基极限承载力降低越快。当雨水以最大降雨强度qB=0.36 cm/h持续入渗5 d后，地基极限承载力由最初的414.6 kPa降低为315.1 kPa，降幅达24%。

3 结论

1) 获得了雨水入渗过程均质地基瞬态极限承载力表达式，建立了极限承载力与地基土体物理力学参数、基础形状和尺寸、降雨强度和降雨历时、地下水位位置之间的映射关系，为研究和评价雨季地基极限承载性能演化特性提供了一种便捷分析方法。

2) 雨水入渗会快速改变地基中上部土体基质吸力的大小和分布，使之沿深度呈现非线性分布特征，进而弱化地基极限承载性能。地基极限承载力受基底以下1.5倍基础宽度应力球范围内平均基质吸力的显著影响，随着雨水入渗时间或降雨强度增加而快速降低，最终在应力范围内土体逐渐饱和并降低至最小值。

3) 根据降雨作用下地基基质吸力与极限承载力演化规律，建议重点做好基底以下1.5倍基础宽度范围内防渗排水工作，特别要加强降雨初期基质吸力监测，防止雨水入渗引起地基承载性能大幅降低诱发地基失稳破坏。

本文的研究以均质地基为对象，假定遭遇均匀型降雨入渗且地下水位维持不变，在后续工作中将丰富降雨雨型，考虑水位波动影响，更深入揭示雨水入渗作用下地基极限承载力演化规律，为雨季地基工程防灾减灾提供技术支持。