基于啁啾莫尔光栅的多波长滤波器研究

丁海波，张培培

(中国船舶集团有限公司第八研究院，江苏 扬州 225101)

0 引 言

光纤通信、光纤传感、光信息处理等新技术的快速发展促进了人们对光纤通信相关器件的研究，涌现出了各种光有源和无源器件。光纤光栅作为一种新型的光无源器件，是根据光纤的反射特性制作的，因此具有良好的光谱特性和稳定的选频特性，受到人们的广泛关注，是光纤通讯发展史上的又一重要标志。随着光纤光栅领域的快速进展，根据光纤光栅的独特性质形成的F-P腔也出现了[1]。由于光纤光栅的多样性等特点，可以通过调整光栅的参数来制作不同功能的F-P谐振腔，在光纤通信器件、光纤传感器件及光纤激光器件等领域应用极其广泛。

本文讨论了一种特殊的啁啾光栅F-P谐振腔，即2个啁啾光纤光栅以一定相对偏移长度重叠写入到光纤内，构成的器件叫做啁啾莫尔光纤光栅[2]。

1 啁啾莫尔光栅

啁啾莫尔光栅，也叫分布式F-P谐振腔，它是一种由2个光纤光栅构成F-P腔的特殊情况，即2个光栅以相对偏移长度D重叠写入到光纤内[3]。啁啾莫尔光栅拥有多通道滤波的特征，通过阻止光谱带中某些频率的光而使特定频率的光通过，可以作为一种带通滤波器，引起了科学家对它的广泛研究。本节对啁啾莫尔光纤光栅的特性进行了理论分析。它的调制示意图如图1所示。

图1 啁啾莫尔光纤光栅示意图

耦合模理论是研究光纤光栅的最基础、最常用的方法，它的特点是能够清楚地描述光信号在波导器件里面的传输、反射特性等物理行为。此外，它还有直观、严谨、准确等优点，特别适合于简单光纤光栅，还能够和传输矩阵法一起构造一些结构复杂的光纤光栅，比如啁啾莫尔光纤光栅等复杂光栅[4]。

根据耦合模理论，表示光纤光栅中前向和后向基模之间的耦合模方程为：

则普通单模光栅的光场强分布满足以下方程:

(3)

式中:E+和E-表示光纤光栅某点的前、后向光场强；σ表示直流部分的耦合系数；κ表示复耦合系数。

其中复耦合系数κ的幅值和相位分别反映了折射率调制的强度和调制包络函数的相位沿光栅长度上的分布情况。

若光纤光栅是啁啾莫尔光栅，则κ的表达式如下：

(4)

式中：A(z)表示切趾函数；κi表示第i次写入的耦合系数。

其中光栅z点处的相位表达式为：

φi=βi(z)·z+φ0i

(5)

式中：βi(z)表示z点处的传输常数；φ0i表示初始相位。

本文研究的是二层啁啾莫尔光栅，即N=2，通过相位掩模板技术即可制成。对传输常数βi(z)进行级数展开，可以得到下式：

i=1,2,z1=0,z2=D

(6)

式中：Λpm表示初始周期；Cpm表示啁啾系数；D表示相对偏移长度。

对于线性啁啾相位掩模板，耦合系数表达式近似为：

κ(z)=|κ(z)|·exp(-jφ(z))=

(7)

其中：

(8)

基于以上分析可以看出：相对偏移长度、啁啾系数等参数会对光栅特性产生影响，所以本文采用传输矩阵法对啁啾莫尔光栅进行分析。

2 传输矩阵法

目前，传输矩阵法是研究一些复杂结构光纤光栅的常用方法，它的特点是不用经过复杂繁琐的推导，而是利用Maxwell方程组，直接通过数值分析法求解，可以研究光波在各种导波介质中的传输性质[5]。所以，这种方法是研究复杂结构的光纤光栅特性的重要手段，拥有准确、灵活、简洁以及快速等优点，尤其适合于对啁啾相移光栅等复杂结构光纤光栅的研究。传输矩阵法的缺点是在折射率发生骤变时的区域会出错，而且对于非均匀的光纤光栅结构，运算会很繁琐。此外，由于计算过程的自动化，某些物理过程一定程度上会受到影响，因此模拟过程的真实性会受到限制。

传输矩阵法是将复杂结构的光纤光栅均分为若干段，需要每段光栅的长度远远超过周期，因此每段光栅能够当作均匀的光栅，可以根据均匀的光栅将其写成一个传输矩阵，然后将得到的每个传输矩阵依次相乘，就能够获得完整的复杂结构光栅的特性。这种方法的运算速率非常快，获得的精确度也很高。

下面是对非均匀光纤光栅利用传输矩阵法的分析过程。

对于长度是L的非均匀的光纤光栅，如果平均分成N段，那么每一段光栅的长度就是z=L/N，同时需要确保每段光纤光栅的折射率是变化平缓的，因此每段光栅能被看作均匀光栅，分析示意图如图2所示。

图2 非均匀光栅矩阵法分析图

假设光波经过第i段光纤光栅的正向电场和反向光场分别是Ri和Si，那么经过第i-1段光纤光栅的正向电场和反向光场分别是Ri-1和Si-1，则它们的关系是：

(9)

其中：

(10)

假设光从光栅的左端入射，边界条件为R0=1，S0=0，逐段迭代可以获得最终输出光场为：

(11)

当折射率调制发生相位骤变时，乘以如下矩阵：

(12)

式中：φi是光波经过相位骤变区域时发生的相位改变量，进而能够获得光纤光栅的反射特性R和透射特性T的表达式分别如下：

R=|F21/F11|2

(13)

T=1-R

(14)

通过上面分析可知，传输矩阵法能够对每段光纤光栅独立地改变相关参数值，因此可以分析非均匀光栅等复杂结构的光栅。本文研究啁啾光栅形成的F-P腔的特性时采取的就是传输矩阵法。

3 仿真与分析

本章结合传输矩阵法和MATLAB软件仿真了啁啾莫尔光栅的反射谱，分别分析了相对偏移长度、光栅长度、啁啾系数等参数变化对啁啾莫尔光栅反射特性的影响。

3.1 相对偏移长度的影响

为了分析方便，假设2个光栅的长度值、啁啾系数值、有效折射率值、折射率调制深度值都相等，令其分别为L=1 cm，C1=C2=0.2 nm/mm，neff=1.443 5，ΔN=10-4。当相对偏移长度值分别是D=1 mm、D=1.5 mm和D=2 mm时，利用MATLAB仿真分析啁啾莫尔光栅反射特性的变化情况。

利用MATLAB仿真得到的反射谱图如图3所示。

图3 不同相对偏移长度的反射谱

自由谱范围(FSR)是研究光纤光栅特性的一个重要参数，推导得到啁啾莫尔光栅的FSR表达式如下：

(15)

式中：C1和C2为啁啾系数；ΔN为折射率调制深度；D为相对偏移长度；λ0为起始波长。

从上式可以看出，啁啾莫尔光栅的FSR与相对偏移长度D、光栅长度、啁啾系数C、折射率调制深度ΔN等参数有关。

表1 不同相对偏移长度的反射谱FSR值

通过不同相对偏移长度的反射谱图和FSR值表分析可得，随着光栅的相对偏移长度的增大，反射谱中谐振峰的宽度会减小，并且反射峰会增加；反射谱的FSR会减小，FSR值与相对偏移长度D是近似反比的关系；另外仿真得到的FSR值与理论FSR值接近，说明仿真结果准确。

3.2 光栅长度的影响

假设2个光栅的相对偏移长度、啁啾系数值、有效折射率的值以及折射率调制深度值等都相等，令它们的值分别是D=1 mm，C1=C2=0.2 nm/mm，neff=1.443 5，ΔN=10-4。当光纤长度值的分别是L=1 cm、L=1.4 cm和L=1.6 cm时，利用MATLAB仿真分析啁啾莫尔光栅反射特性的变化情况。

利用MATLAB仿真得到反射谱图如图4所示。不同光栅长度的反射谱FSR值如表2所示。

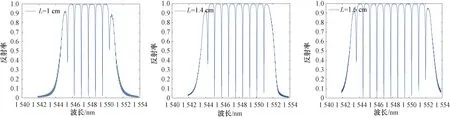
图4 不同光栅长度的反射谱

表2 不同光栅长度的反射谱FSR值

通过不同光栅长度的反射谱图和FSR值表分析可得，如果啁啾莫尔光栅的长度值增大时，反射光谱中的FSR值保持恒定，并且反射谱中的反射峰个数会逐渐增加。

3.3 啁啾系数的影响

假设2个光栅的相对偏移长度值、光栅长度值、有效折射率值和折射率调制深度值等都相等，令它们的值分别是D=1 mm，L=1 cm，neff=1.443 5，ΔN=10-4。当构成啁啾莫尔光栅的2个光栅啁啾系数值分别是C1=0.2 nm/mm和C2=0.19 nm/mm、C1=C2=0.2 nm/mm、C1=0.2 nm/mm和C2=0.22 nm/mm时，利用MATLAB仿真分析啁啾莫尔光栅反射特性的变化情况。

利用MATLAB仿真得到反射谱图如图5所示。

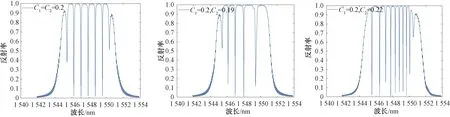
图5 不同啁啾系数的反射谱

通过不同啁啾系数的反射谱分析可得，啁啾莫尔光栅的反射谱中的FSR受2个光栅的啁啾系数影响，并且FSR的变化趋势与2个光栅的啁啾系数都相关；在同一反射谱中，FSR的大小随着波长线性变化。

4 结束语

本文首先借助耦合模理论对啁啾莫尔光纤光栅进行了理论分析，然后介绍了传输矩阵法的原理，在此基础上结合MATLAB软件仿真了啁啾莫尔光纤光栅的反射谱，并分别改变相对偏移长度、光栅长度和啁啾系数等参数，分析了这些参数对反射谱及FSR值的影响情况。研究结果有助于光纤光栅F-P腔在微波光子雷达、多波长滤波器、多波长激光输出等领域的应用。