基于网格搜索与交叉验证的SVR 大型拖拉机销量预测
张杨航 ,吕 锋*,李锋军,张雷雷,苏建新
(1.河南科技大学 机电工程学院,河南 洛阳 471003;2.第一拖拉机股份有限公司,河南 洛阳 471004)
农机装备是“中国制造2025”战略的十大重点领域之一,是支撑我国农业生产和发展的重要基础和战略性产业。 农机装备市场需求量季节性变化明显,需求高峰月份与低谷月份的销量差别巨大。准确预测农机装备销量是整个农机装备企业供应链管理中的重要环节,利于企业合理制定生产计划,可减少需求高峰期“断供”或积压过多库存造成的损失。拖拉机作为各类农机装备的动力源, 具有适用范围广泛的优势,同时政策补贴力度较大,是农机装备市场的热点。 相比于小型拖拉机,大型拖拉机生产难度较大、造价较高且更适于土地流转后集中连片作业,因此,针对大型拖拉机的销量预测具有重要意义。
传统销量预测研究集中于时间序列模型和回归预测模型应用研究, 例如移动平均法、 指数平滑法、ARMA 法、多元回归法,这些销量预测模型在电商、汽车等多个领域得到了广泛的应用[1-2]。 与其他产品相比, 大型拖拉机销量受经济环境和补贴政策影响较大,时间序列模型仅能识别自身过去或滞后值之间的内在关系,无法确定各影响因素对销量的影响。 回归预测模型缺乏数据样本学习过程,易导致非线性关系模糊、 计算过程复杂,难以取得令人满意的预测效果[3]。随着人工智能的发展,基于机器学习的智能预测方法成为近年来的研究重点,如人工神经网络和支持向量机(Support Vector machine,SVM)[4]。 人工神经网络模型的预测效果依赖于数据量的大小,而拖拉机月度销售量的预测更依赖新信息, 如果可用数据较少,则人工神经网络很难取得良好的样本外表现[5]。 SVR是SVM 对回归问题的一种运用, 可有效解决预测中小样本、非线性等问题,且在高维模式识别中表现出一定优势,被广泛应用于电力预测、客运需求预测等领域。
在SVR 预测模型的具体应用中, 惩罚系数C 和核函数参数g 的选取对预测性能具有关键性的影响。在机器学习领域,各类启发式算法因其强大的优化性能而被广泛应用于模型的参数优化,如Tharwat. A等[6]使用量子粒子群优化算法对SVM 超参数进行优化;Zhou Tao 等[7]使用遗传算法对SVM 超参数进行优化, 提高了模型预测精度和计算速度;Kapoor. K等[8]使用基于灰狼优化的SVM,得到最佳参数组合,获得最优二值分类结果。 但是,这些启发式算法均从随机的可行初始解出发,采用迭代改进策略,去逼近问题的最优解, 而不是系统地以确定的步骤去寻求答案,因而无法保证收敛到最优点。网格搜索与交叉验证法可以通过循环遍历,尝试每一种可能性,进而找出全局最优点,并在参数较少的情况下,也不存在计算时间过长的问题, 因此被广泛应用于SVM 的参数优化中。 雷会平等[9]提出一种改进的网格搜索和交叉验证方法, 建立了复杂水体硝酸盐浓度的SVR 预测模型,有效提升了预测精度和训练效率;奚杏杏等[10]使用基于网格搜索与交叉验证相结合的SVR 模型对血压进行预测, 结果表明该模型的预测准确率和方根误差值均明显优于传统的机器学习算法;Wang Zhenhe 等使用GS-SVM 作为优化分类器,对虫害持续时间进行判别, 表现出较好的分类性能。在参考现有研究成果的基础上, 综合考虑季节、农业经济环境和农机补贴政策影响,引入基于网格搜索和交叉验证的支持向量回归模型(GSCV-SVR),对大型拖拉机销量进行预测研究, 以期获得更高的预测精度。
1 变量选取与数据处理
1.1 变量选取
参考现有研究成果,结合数据可得性,选取如表1 所示的若干变量作为影响因素预测销量。 其中,第一产业人员从业数量、 农村居民可支配收入指数、农作物播种面积和农机补贴额为每年年末统计数据,采用线性插值法充填为月度数据。主要农作物和柴油价格取上月月初和月末的平均价格。

表1 各变量类别及名称Table 1 Category and name of each variable
1.2 数据预处理
月份是影响大型拖拉机销量的重要离散型分类特征, 普通编码方式会体现特征值之间的大小关系,造成模型预测误差。为使特征值之间距离计算更加合理,经常对离散型特征使用One-Hot 编码,将特征数值表示为二进制向量,并将这些向量作为模型训练特征,以有效提高模型预测精度。 使用One-Hot 编码方法对月份进行编码,如图1 所示。

图1 各月份的ONE-HOT 编码Figure 1 ONE-HOT code for each month
为消除不同维度数据间的量纲差别,需对除月份之外的数据进行归一化处理:

2 基于网格搜索与交叉验证的SVR
2.1 支持向量回归
SVM 是按监督学习方式对数据进行二元分类的广义线性分类器,SVR 是SVM 由分类问题到回归问题的推广,是SVM 的重要应用分支。 设样本集为(xi,yi),i=1,2,3,K,n, SVR 通过非线性映射将回归数据映射到高维空间,在高维空间构建回归函数:

式中,ω 为权向量;b 为偏置量;φ 为核函数, ω和b 可以通过求解最优分类面函数的最小化获取:

式中,C 为惩罚系数;ξi和为松弛变量;ε 为取值为任意正数的偏差。
使用拉格朗日乘子法计算得到:

由于输入特征与销量数据间呈现高度的非线性关系,特选择径向基核函数(RBF)进行回归数据的高维映射,表示为:

式中,K(X,X′)为满足 Mercer 条件的核函数;g为核函数参数。
计算得到SVR 模型为:

2.2 改进的网格搜索与交叉验证
K 折交叉验证法将训练数据等分为K 个子集,选择任一子集作为测试集,其他子集作为训练集进行交叉验证, 重复K 次, 找到均方误差最小的参数组合,并将得到的最优参数输入到SVR 模型中,具体如图2 所示。

图2 交叉验证详解图Figure 2 Detail figure of cross validation
网格搜索法即采用穷举搜索的方式,在指定的参数范围内按步长依次对参数组合进行搜索。本研究提出一种改进的网格搜索法,即通过不断收缩网格大小和步长来达到更高精度并有效提高搜索效率。改进的网格搜索与交叉验证法具体步骤如下:
第一步:设定参数和的取值范围[2N,2N],设定初始步长为M,获得一个粗网格,网格中的节点即为给定范围内所有可能得到的参数组合。
第二步:对所有参数组合使用交叉验证法进行评价,找到均方误差最小的参数组合(Ci,gi)。
第三步:选取参数组合(Ci,gi)相邻两个节点间的网格作为新的参数组合选择范围,并设定搜索步长为,再次进行交叉验证,找到新的均方误差最小的参数组合(Ci,gi)。
第四步:若(Ci,gi)在交叉验证中均方误差满足精度要求,储存(Ci,gi)至 SVR 模型,反之则转到第三步,直至(Ci,gi)在交叉验证中均方误差满足精度要求。
网格搜索与交叉验证法以参数均方误差最小化为目标,以参数范围为约束条件,遍历每个可能的参数组合,避免了局部最优解的存在,可有效提高参数优选的准确性。
GSCV-SVR 大型拖拉机销量预测模型流程如图3 所示。

图3 GSCV-SVR 大型拖拉机销量预测模型流程图Figure 3 Flow chart of GSCV-SVR large tractor sales prediction model
3 实证分析
以2017—2021 年某品牌某型号大型拖拉机在河南省的销量数据为基础,对农机装备销量预测进行实例分析,具体数据如图4 所示。

图4 2017—2021 年某品牌某型号拖拉机的河南销量数据Figure 4 Sales data of a brand and model of tractor in Henan Province from 2017 to 2021
取2017—2020 年的销量数据作为训练数据,对2021 年的数据进行预测;与2021 年的实际销量数据进行对比,计算预测误差,评价模型的准确性.
首先对数据进行预处理,之后设定模型中惩罚系数和核函数参数的初始范围为[2~8,28],初始步长为1。针对所选的数据集特征,交叉验证CV 参数K 选择4。通过网格搜索与交叉验证确定最佳参数组合,得到GSCV-SVR 预测模型。 将2021 年自变量数据输入GSCV-SVR 预测模型,得到预测结果。 预测结果与实际数据对比如图5 所示。

图5 GSCV-SVR 预测值与实际值对比图Figure 5 Comparison of GSCV-SVR predicted value and actual value
为进一步检验GSCV-SVR 在大型拖拉机销量预测上的准确性, 分别使用 LSTM 人工神经网络、ARIMA、LASSO 回归常用预测模型, 对 2021 年销量数据进行预测。各模型预测结果与实际数据对比如图6 所示。
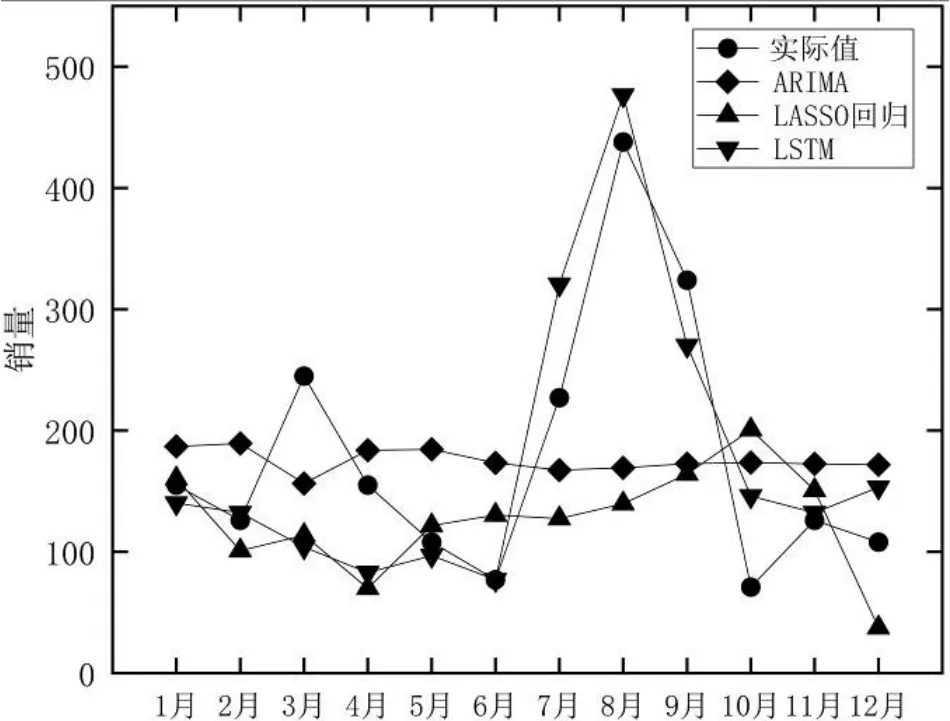
图6 各预测模型结果对比图Figure 6 Comparison diagram of the results of each prediction model
表2 给出了各模型预测结果与实际数据的均方根误差(RMSE)和平均绝对误差(MAE),由此可知GSCV-SVR 的均方根误差和平均绝对误差均最小,相比其他预测模型具有更好的预测性能。

表2 各模型预测效果对比Table 2 Comparison of the prediction effects of each model
4 结论与展望
将SVR 方法应用于大型拖拉机销量预测研究中,可有效解决预测研究中历史数据量少、影响因素多的问题。 提出一种改进的网格搜索与交叉验证法,用于SVR 参数寻优并可有效提高网格搜索的精度和效率。通过分析选取影响销量的特征并将其归一化和One-Hot 编码处理,作为模型的输入,以增强模型的可解释性,提高预测精度。预测结果表明,在小样本情况下,利用RBF 核函数建立的GSCV-SVR 模型相比于LSTM、ARIMA 和LASSO 回归模型具有更高的精度,能够用于大型拖拉机的销量预测。

