膨胀土边坡稳定性理论计算方法对比研究

王森 陈涛 翁运新

（1.中铁二院重庆勘察设计研究院有限责任公司，重庆 400023；2.中铁城市发展投资集团有限公司，成都 610000；）3.中铁二院工程集团有限责任公司，成都 610031）

膨胀土边坡是一种以膨胀土为主要土质成分的特殊边坡，此类边坡通常会因遇水膨胀、失水收缩等特性而在坡体上产生许多裂隙，从而导致边坡土体发生失稳，引起土体坍塌、滑坡等自然灾害。

针对膨胀土边坡稳定性的分析受到了国内外众多专家学者的积极关注和深入研究，此类课题逐渐成为岩体工程领域乃至土木工程领域中热点课题［1-3］。当前，针对膨胀土边坡的稳定性分析普遍采用极限平衡法进行研究，主要方法包含：Fellenius 法［4］（假设土条间的作用力忽略不计）、Morgenstern-Price 法［5］、简化Bishop 法［6］（毕肖普法，考虑土条间作用力）和Spencer 法［7］。利用Geo-Slop 软件，祝方才［8］等在天然与饱和两种状态下应用4 种极限平衡方法分别对深圳高速公路的路堑边坡稳定性进行对比研究，最终针对性提出了该边坡的支护手段；针对Fellenius 法，根据某工程实例，李闯［9］等利用微分法建立数学模型对其进行分析，并求解该边坡的安全系数K；刘茂［10］等利用简化Bishop 法对圆弧形滑动面土质坡体进行稳定性评价，推导出与之相适应的下滑推理解析计算公式；在充分考虑孔隙水渗流的情况下，杨建民［11］等使用Morgenstern-Price 法分别对两个工程算例的有效应力进行计算验证，证明了此方法的准确性和有效性；基于Spencer 法，陈昌富［12］等采用斜条分法土质边坡的位移进行计算，在考虑滑动面抗剪强度震动衰减的影响下，提出一种新的计算方法，并用试验证明了该方法适应性广泛、计算精度高的特点。

本文通过引入膨胀力分别探讨4 种边坡稳定性分析方法的计算原理及过程，结合国内西部某工程实例，对引入膨胀力前后的膨胀土边坡稳定性系数进行计算和对比，以探究这4 类方法对膨胀土边坡的适宜性和准确性，研究成果可为今后研究膨胀土边坡稳定性问题提供参考依据。

1 膨胀力的引入

膨胀力是由土体吸水发生体积膨胀而产生的一种面力，先前研究发现土体的膨胀力能减小因剪切强度而产生的作用力。此膨胀土类边坡的膨胀力作用范围受到土体含水量的变化影响很大，并且受大气影响也较为显著，土体的含水量也随着当地天气的原因而出现较大的波动。同时，随着土层的增加，土体膨胀力波动范围也逐渐减小，当土层达到一定深度，土体的膨胀力将会趋于某个稳定值。土体膨胀力影响范围如图1所示。

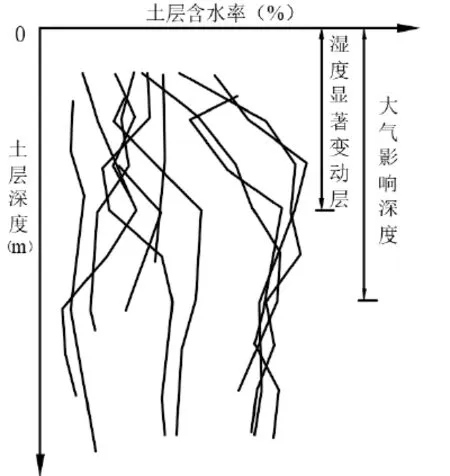
图 1 膨胀土的湿度随深度变化曲线图

根据摩尔库伦（Mohr-Coulomb）强度准则，现对膨胀土做一个简要的力学分析，推导出考虑膨胀力的抗剪强度表达式为：

式中：σ——法向压应力；

p——沿作用面法向的膨胀力；

c——膨胀土的粘聚力；

2 几种边坡稳定性方法计算理论

2.1 Fellenius法

膨胀土边坡应用Fellenius 法的计算简图如图2所示。该方法的计算原理即是将滑动体竖向平均划分为n 条土体单元，将其中一条土体单元单独拿出来进行受力分析，并假定每个相邻的土体单元之间不存在任何作用力，最后通过计算滑动面上整个土体的抗滑力矩与下滑力矩之间的关系就可求出膨胀土边坡的稳定性系数K。

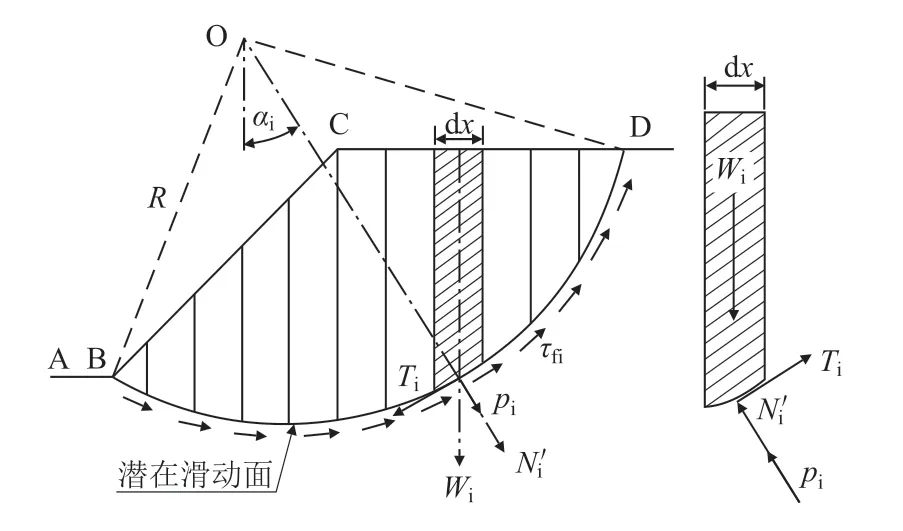
图2 Fellenius 法计算简图

单个土条单元的法向应力为Ni＇和切向应力为Ti，假定滑动面处的膨胀力Pi作用在每个土条底部的中点，则对于第i 个土条单元位于滑动面上土的抗剪强度为：

而某个土体单元需要满足水平方向和竖向方向的静力平衡条件为：

根据Fellenius 法，将膨胀土边坡滑动面上土体的抗滑力矩Mr与下滑力矩Ms作比值：

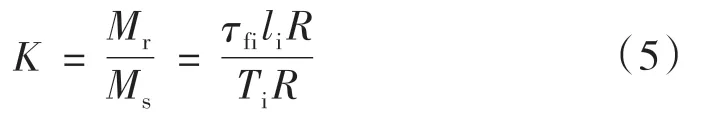
现将式（2）代入到第i 个土体单元的滑动面抗剪强度分析的公式中，得出Fellenius 简化条分法关于膨胀土边坡稳定性系数K 值的表达式为：

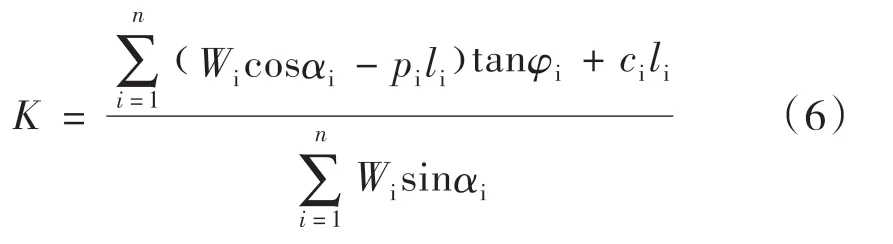
式中：Wi——第i 个土条单元的重度；

Pi——滑动面上第i 个土体单元的膨胀力；

li——第i 个土条单元滑动面处的长度；

R——圆弧滑动面半径；

Ti——第i 个土条单元的切向应力；

αi——第i 个土条单元滑动面的倾角。

2.2 Bishop法

Bishop 法是一种应用范围较为广泛、分析计算过程简洁的条分方法，在不同情况下该方法的计算结果都很准确，但该方法的不足之处是仅能用于圆弧滑裂面和数值分析问题方面的研究。与Fellenius 法相比，Bishop 方法主要考虑了单元土体之间的作用力，此外，Bishop 方法还认为在单元土体底部滑动面上的抗滑安全系数，与整个膨胀土边坡滑动面的安全系数相同。Bishop 方法的计算模型如图3所示。

图3 Bishop 法计算简图

假定每个单元土条两侧的竖向剪切力大小相等，即，Ei+Ei+1则边坡潜在滑动面上每处土体的抗剪强度与相应方向的剪应力之比为：

单元土条竖直方向力的平衡条件为：

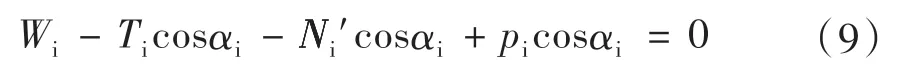
根据极限平衡法的应用条件，得出应用Bishop 条分法的膨胀土边坡的稳定性系数K 的表达式为：

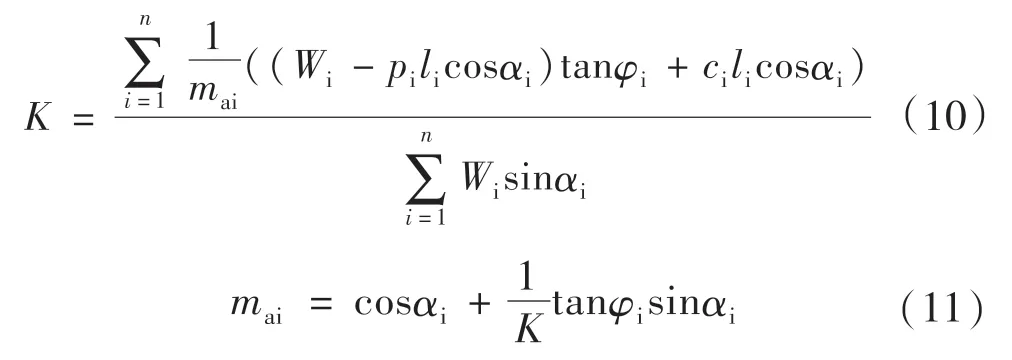
由式（10）可得，膨胀土边坡的稳定性系数K 与mai值之间存在相互迭代的关系，因此在确定两者的值时应首先假定一个K 值，并通过式（11）求得mai的值，然后再代入式（10）中求取K 值，若计算所求得的K 值与假定的K 值不符合，则重复上述过程重新计算K 值和mai的值，经过反复迭代计算直到K 值与假定的值相近（或满足预先设计精度的要求）为止。

2.3 Morgenstern-Price法

Morgenstern-Price 法被国际学术学会与广大研究学者认为在边坡稳定性分析方面最具适应性和最具严谨性。该方法能同时满足力和力矩均平衡的两个条件。对于任意类型的坡体滑动面，第i 个单元土条的受力分析模型均可以简化，如图4所示。Morgenstern-Price 法应用的前提条件是，两个相邻单元土条的法向条间力Ei和切向条间力Xi之间存在一个函数关系：

图4 Morgenstern-Price 法土条分析图

式中：λ——任意常数；

为方便计算迭代，假定第i 个单元土条两侧的总法向力Ei等于条间膨胀力Pi与有效法向力之和，并且Ei和Ei+1在第i 个单元土条两侧的作用点距土体滑动面的高度分别为yi和yi+1：

将膨胀土滑动带均分为n个单元土条，一个单元土条的自重力Wi和单元土体的条间膨胀力Pi均已知，单元土条两侧的总法向力Ei、Ei+1；单元土体的切向条间力Xi、Xi+1；作用点距滑动面的高度yi、yi+1；法向应力；切边应力Ti和常数λ为未知量，合计共8n+2个未知量。

在单元土条之间的界面上，根据力具有连续的性质，可得到2（n+1）个方程：

由滑动面的抗剪强度方程，合计共n 个方程：

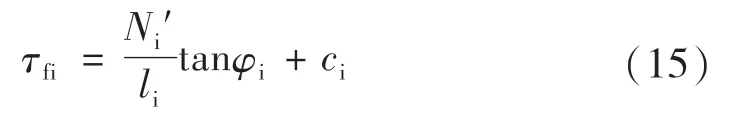
根据单元土条两侧的总法向力Ei与其切向条间力Xi之间存在的函数关系，合计共2n 个方程：

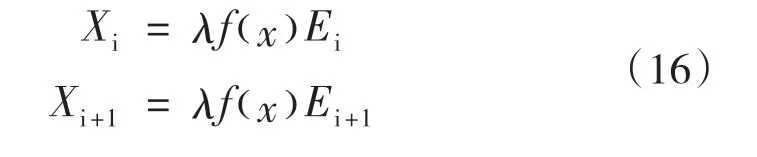
则根据单元土条的静力平衡方程共3n 个：

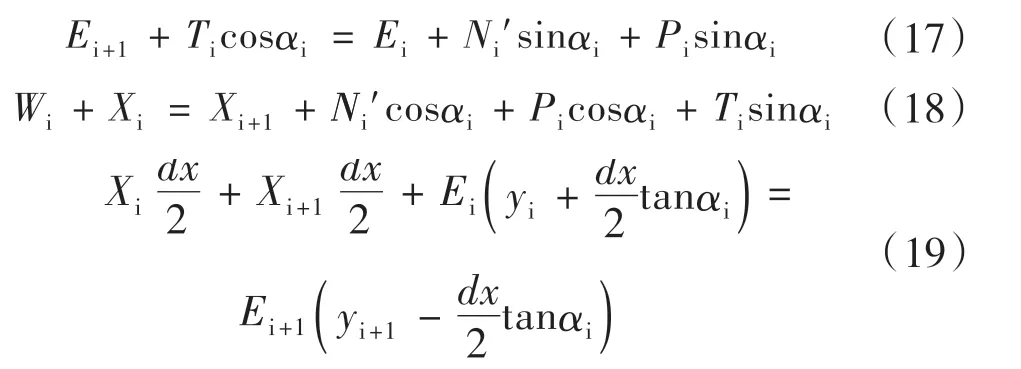
当整个滑动土体上没有其他力作用时，则第i 和第n 个单元土条之间必须满足以下两个关系式，即：将式（12）～ 式（21）进行联立求解即可得到考虑膨胀土边坡的稳定系数K。

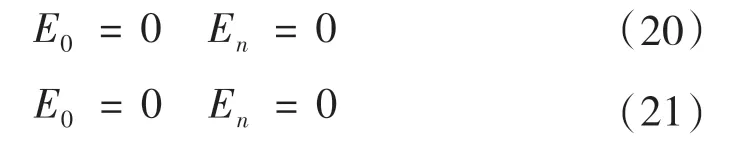
2.4 Spencer法

Spencer 法是被广泛应用于土质边坡稳定性分析的方法之一［7］，其采用总应力法对整个边坡进行分析求解。通过对一个土条单元进行受力，将坡体土条单元进行力和力矩的平衡分析，假定各个土条之间作用力的合理平行，而后对土质边坡进行安全系数求解。现将本分析方法进行图解描述，将第i 个土条单元进行受力分析，如图5所示。

图5 Spencer 法土条分析简图

假设相邻的单元土条之间的法向条间力Ei不与切向条间力Ti之间存在以下关系：

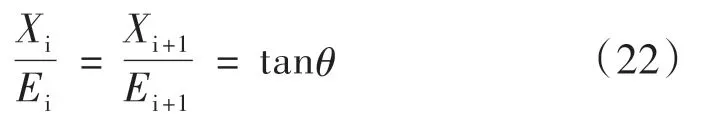
相邻的两个垂直单元土条底部力的平衡方程为：

相邻两个平行单元土条底部力的平衡方程为：

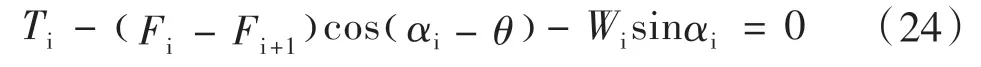
再按照稳定性系数定义的M-C 准则可得：

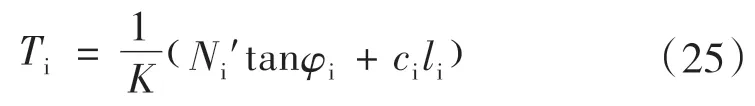
则土条两侧条间力的合力为：

整个滑动坡体应该满足的力平衡和力矩平衡：

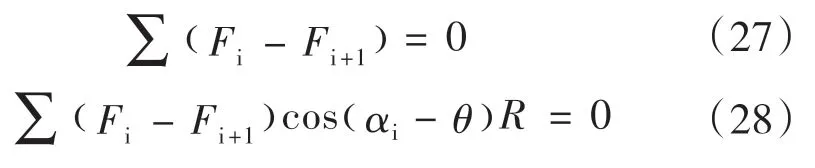
式中：Fi——第i 个单元土条两侧条间力的合力。

联立式（22）～式 （28），根据极限平衡法的条件，可通过Spencer 法得到考虑膨胀力下的土质边坡稳定性系数K。

3 工程实例

选取西南地区某膨胀土边坡工程实例进行分析研究，边坡坡高10.0 m，坡脚40° ，在坡底5.0 m 范围内没有发现地下水。坡面护坡采用混凝土进行喷射，但其防渗能力较差，在多雨情况下，会有严重的失稳现象。为简化计算，将边坡土体设置为均质土，对开挖膨胀土边坡进行计算分析。室内试验测得该边坡土质的膨胀力最大值约为29.5 kPa，自由膨胀率为54.1%。膨胀土边坡物理参数如表1所示，绘制膨胀土边坡横断面如图6所示。

表1 膨胀土的物理参数表

图6 边坡横断面示意图

分别采用Fellenius 法、Bishop 法、Morgenstern-Price 法和Spencer 法对选取的膨胀土边坡模型的稳定系数进行计算分析，针对考虑膨胀力（工况Ⅰ）对膨胀土边坡进行极限平衡分析，并将分析结果与不考虑膨胀力（工况Ⅱ）计算结果进行对比分析。4 种极限平衡法的结果对比如表2所示。

表2 极限平衡法计算结果对比表

由表2可知，Fellenius 法、Bishop 法、Morgenstern-Price 法和Spencer 法在考虑膨胀力的作用下，其边坡稳定系数分别为0.454、0.471、0.508 和0.502；对比不考虑膨胀力的稳定性系数进行分析，其边坡稳定性系数降低了20%～30%；由此可知，考虑膨胀力的边坡稳定性系数更偏于保守，将膨胀力考虑在边坡稳定性分析中能够更好的保证边坡的稳定性。4 种极限平衡法，计算出的边坡稳定系数基本相近，Fellenius 法计算得到的稳定性系数更小，即采用Fellenius 法对边坡的稳定性分析更偏于安全。

膨胀力是膨胀土这种特殊土体的一种重要特性，建立新的膨胀土边坡模型，模型坡高6.0 m，坡脚呈49°、土的黏聚力c=15 kPa、内摩擦角ψ=7.4°，重度=18.0 kN／m3。在考虑膨胀力的基础上，分别采用Fellenius 法、简 化Bishop 法、Morgenstern-Price 法 和Spencer 法对边坡的最危险滑动面进行搜索，经过反复迭代计算后得到边坡的最危险滑动面以及边坡稳定系数K 值，各方法的滑动面和K 值如图7所示。

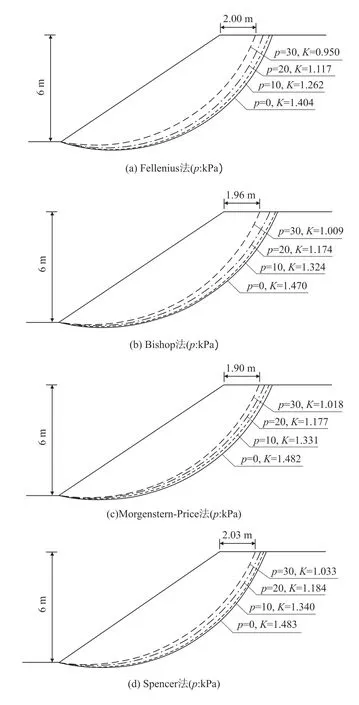
图7 膨胀力对边坡稳定性的影响图

4 种方法的边坡稳定系数随膨胀力的变化曲线如图8所示。由图8可知，随着膨胀力的增加，4 种方法计算的稳定系数呈现相同的线性减小，但Fellenius 法计算的稳定系数较其余3 种方法得到的稳定系数偏小；4 种极限平衡法对应滑动面深度随着土质膨胀力的增加而减小，即土质的膨胀力越大，对应边坡的表层也发生滑动的概率越大。

图8 边坡稳定系数随膨胀力变化曲线图

4 结论

（1）通过具体的工程实例对Fellenius 法、Bishop法、Morgenstern-Price 法和Spencer 法等4 种极限平衡法的稳定系数进行比较，发现应用Fellenius 法对边坡的稳定性分析更偏于安全。

（2）通过引入膨胀力对膨胀土边坡进行受力分析，并通过具体工程实例分析考虑膨胀力前后膨胀土边坡安全稳定性的变化，得出考虑膨胀力的作用对边坡的稳定性计算更加偏于安全。

（3）随着土质膨胀力的增加，边坡的稳定系数逐渐减小，即边坡中膨胀土的膨胀力越大，其浅表层发生滑坡的几率越大。

（4）膨胀力相对比较复杂，在今后的实际工程中，需要根据实际情况对膨胀力加以考虑，以便更好地保证边坡的稳定性。