输电线路应急抢修物资调度模型及算法研究

史晓峰，赵耀红

(1.长春工程学院现代教育技术中心，长春 130012； 2.长春大学计算机科学与技术学院，长春 130022)

0 引言

电力系统的稳定运行对维持社会秩序非常重要，一旦发生大规模甚至长时间的停电事故，将对社会稳定和经济发展带来严重的不良后果。因此，当停电发生后，如何快速及时地对电力系统进行恢复意义重大。其中，应急抢修物资的调度最耗费车辆、人力和时间，在非常时期如何能够合理、高效地调度物资，节省时间和费用等，值得深入研究。

国内外学者对应急物资调度问题进行了一系列研究，Shi等[1]以距离最短为目标构建调度模型，一车服务一需求点。Vidal等[2]建立的调度模型带有时间限制，考虑了多个供应点问题，实现了物资的多次配送。苏涛等[3]建立了物流配送模型，注重配送费用最小化。Berkoune等[4]建立的模型考虑了多需求点和多供货点，以总运输时间最少为目标。陈勤等[5]建立了多目标模型，考虑了运送费用、运送时间和安全性指数，但对需求量和车辆运输能力考虑不周。

目前针对应急物资调度模型的研究大多数以耗时最少、费用最小或者路程最短为目标来展开，但对运输能力考虑较少，在解决实际问题时，满足应急调度时间和费用最少的同时，应考虑同一应急资源供应点可能多次参与调运，这样更加贴近现实。

1 输电线路应急抢修物资调度模型

通常的应急抢修物资调度思路是选择最近的物资供应点进行物资供应。这种选择要求该物资供应点贮存的物资量必须大于等于应急点的需求量，但在实际大规模应急抢修中是不能满足的，因此便出现了多个物资供应点优化调度问题。由于是应急抢修，因此应急资源调度总时间最短是首先要考虑和满足的目标。

在大多数实际抢修中，各供应点都存在运输能力(单次能运送物资的最大量)的限制问题，必须考虑多次运送。因此，在满足调度时间和费用最少的前提下，同时需考虑同一应急物资供应点可能会参与多次调运，这更加贴近实际。同时，需要一种调度算法对该模型进行求解。

本模型解决的是从多供应点往多需求点运往的多种物资调度问题。从输电线路应急抢修物资调度的特点出发，首先考虑应急抢修时间，以时间最短作为优化目标；运输费用也是优化目标之一，目的是在保证抢修时间的前提下，最小化调度中的运输费用；因为每一供应点可能存在多次调运，因此应将各供应点物资的调运能力作为一个约束条件。根据前述优化目标和约束条件建立有运输能力约束的时间和费用最优的应急资源调度模型。

记V1，V2，…，Vm为m个故障发生区域可选的应急物资供应点，A1，A2…，An为n个故障发生点，即需求点；需求点共需要k种应急物资，记X=(Xi1，Xi2，…，Xik)表示故障发生点Ai需要k种物资的量，Xij(j=1，2，…，k)表示需求点Ai对第j种物资的需求量；从Vi一次调度第j种应急物资的最大量为Mij(i=1，2，…，m；j=1，2，…，k)，到达Aj所需的单次调度时间为tij(i=1，2，…，m；j=1，2，…，n)。ttij为Vi到Aj可应急调运的最长时间，ttij为tij的整数倍；T为规定的应急调运限制期；cij为从Vi调度单位第j种应急物资所需的费用，i=1，2，…，m，j=1，2，…，k；VXij为供应点Vi的物资j的供应能力(即存货量)。

模型建立说明：

1)每个供应点每次调度的应急物资的数量≥0，且不全为0，每次调度不超过自身运输能力。

2)各种不同的应急物资的调度互不影响，可单独调度，也可以一起调度。

3)需求点需要的物资种类和数量事先已经确定，调度中不会发生变化。

4)所有供应点的各种物资总量大于等于需求点所需物资总量。

5)所有供应点与需求点的道路都是联通的，每个供应点单次运输物资所需的时间事先已计算得出。

应急抢修物资调度数学模型：

(1)

T)，

(2)

(3)

∑VXij≥∑Xj(i=1，2，…，m，j=1，2，…，k)，

(4)

(5)

Mij≥0(i=1，2，…，m，j=1，2，…，k)，

(6)

(7)

前述模型的建立综合考虑了调度的时间、费用及运输能力，目的是让应急调度的总时间和运输费用最小化。式(1)～(2)为目标函数，代表物资运输时间和费用的最小值。约束条件(3)表示第j种物资需求量小于等于其供应总量。约束条件(4)表示对所有供应点的第j种物资的需求量小于等于其库存量。约束条件(5)表示供应点的第j种物资供应总量小于等于第j种物资供应能力。约束条件(6)表示每次调度的物资数量≥0。约束条件(7)表示当运输能力小于等于库存量时，每次按运送能力运送，否则按库存数量运送。

约束条件不变，分别求得：

可以将目标函数(1)和(2)合并为单目标函数：

(8)

取适应度函数为目标函数(8)式的值。p1和p2分别为运输时间和运输成本在模型中的重要程度，即权值，可根据需要和不同情况人为确定二者的值，且p1+p2=1，例如：时间和费用同样重要时，二者的值均取0.5。

2 输电线路应急抢修物资调度算法

粒子群算法(Particle Swarm Optimization，PSO)基于对鸟群等觅食的模拟，同遗传算法类似。算法初始时随机选取一组解，通过多次循环迭代寻找最优解，但该算法的特点是没有交叉和变异的过程，而是经过所有个体之间的协作来寻找最优解的，即每个粒子不断地在其解空间追踪最优粒子来进行搜索[6]。

PSO初始化为一个种群，由m个随机选择的粒子组成。每个粒子有一个适应度值，由事先建立的优化函数求得，定义所有粒子飞行的方向与距离，粒子搜索的原则是不断追踪最优粒子。每个粒子依据自己找到的最优解(个体极值)和整个种群的最优解(全局极值)或一部分邻居粒子中找到的极值(局部极值)来更新自己。

第i个粒子的位置表示为

(9)

第i个粒子的速度表示为

(10)

第i个粒子经历过的历史最好点表示为

(11)

粒子根据式(12)～(13)来更新其速度和位置：

(12)

(13)

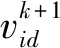
粒子群优化基本算法流程图如图1所示。

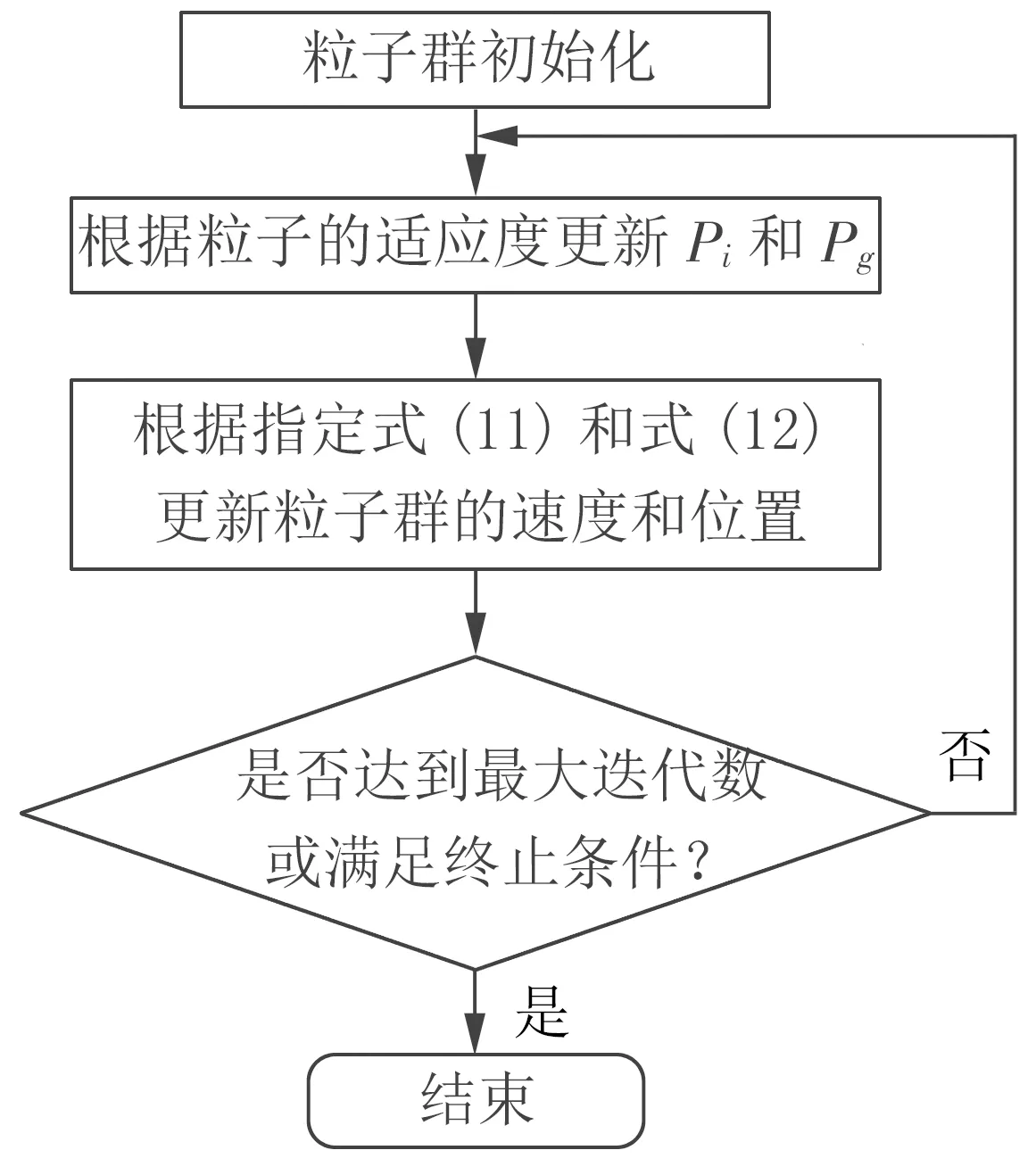
图1 粒子群算法流程图

粒子群算法的特点：结果与初始解无关，因为初始解随机产生。算法具有很好的平衡全局搜索与局部搜索能力，式(12)既体现了搜索的多样性，又保证了搜索向全局最优的方向进行；算法概念易于理解，程序实现简单，能够在复杂的、非线性区域搜索。

遗传算法存在很多问题：

1)易产生未成熟收敛点，收敛到局部最优解，找不到全局最优解，原因是未得到最优解之前，群体已经失去了多样性。

2)快接近最优解时，收敛速度较慢。遗传算法在进化初期能快速收敛，但在进化后期，收敛速度变慢，影响了算法的效率。

混合粒子群遗传算法(Particle Swarm Optimization-Genetic Algorithm，PSO-GA)能够解决遗传算法不成熟收敛问题。算法首先的初始种群为K个家族；通过家族间交叉繁衍保持种群多样性；通过家族内交叉繁衍提高算法的收敛速度；同时进行粒子群交叉，让粒子以一定的“速度”(交叉概率)向本家族适应度值最小的个体靠拢，加速收敛。混合粒子群遗传算法流程图如图2所示。

对PSO-GA算法的描述：1)初始种群生成。随机生成n个个体的初始种群。2)划分家族。将种群分成K个家族(按适应度值)。3)族间交叉。随机选择两个家族的最优个体交叉。4)族内交叉。在同一家族内随机选择不同的个体交叉。5)粒子群交叉。最优个体与该家族的其他个体交叉。6)变异。除了种群中最优的个体(一般为两个)，其他个体按定义好的变异概率执行变异操作。7)若终止条件满足，则结束算法，否则转到2)。

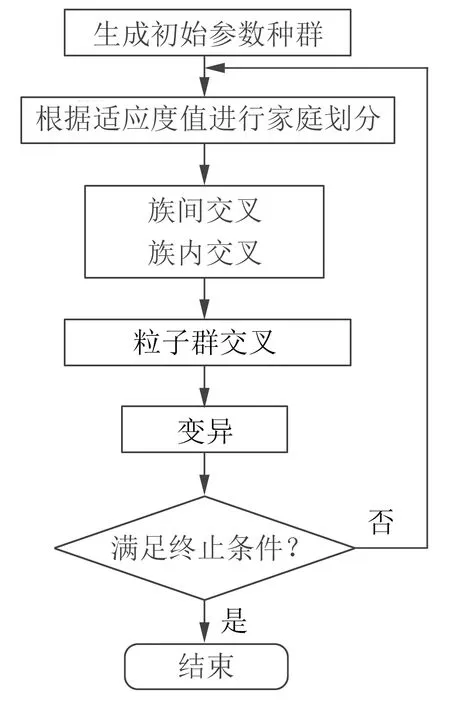
图2 PSO-GA流程图

3 实验与分析

设某地区电力杆塔A1、A2、A3发生故障，需运送抢修物资及时抢修。周边共有3个电力物资供应点V1，V2，V3，抢修物资的供应能力分别为VX1，VX2，VX3。故障点A1、A2、A3需要的抢修物资的量分别为AX1，AX2，AX3。3个电力物资供应点为3个抢修点运送抢修物资的运输能力(单次运输的最大量)分别为M1，M2，M3。3个电力物资供应点运送抢修物资的单次调度时间分别为t1，t2，t3。3个电力物资供应点运送抢修物资的单次运输费用分别为c1，c2，c3。前述详细数据分别见表1～4。

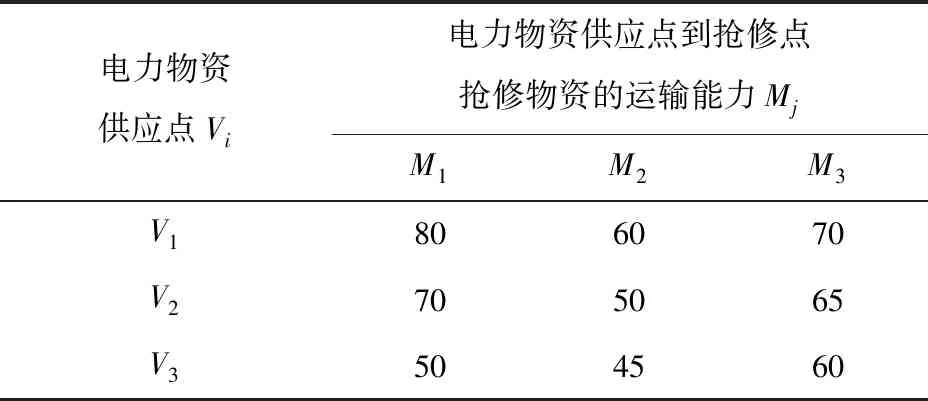
表1 3个供应点抢修物资的运输能力

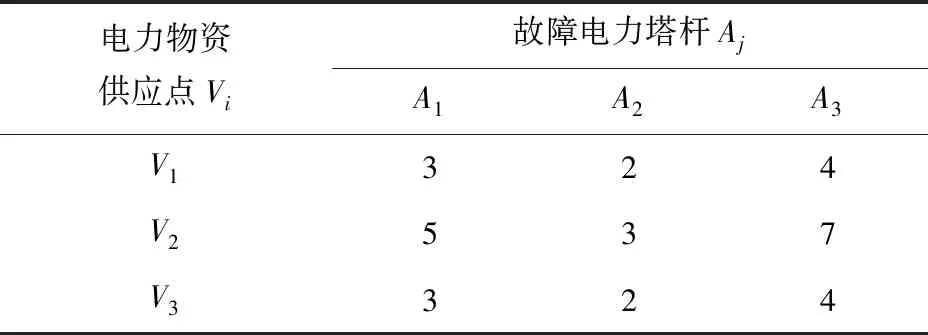
表2 抢修物资从3个供应点到需求点的单次调度时间 单位:h

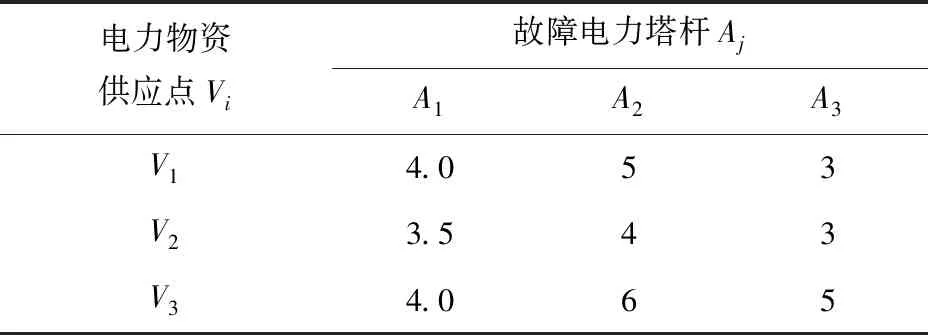
表3 抢修物资从3个供应点到需求点单位的运输费用 单位:万元

表4 抢修物资供应量与需求量

基于前述数据集，比较GA算法和PSO-GA算法的性能。参数设置为：p1=0.7，p2=0.3，分别代表运输时间和运输成本在模型中的重要程度；种群规模n=100；循环迭代次数=20；定义变异概率Pm=0.1；定义交叉概率Pc=0.7。算法的对比结果见表5。与GA算法相比，PSO-GA算法在应急物资调度过程中，能够获得较少的运输时间及运输费用，使抢修更高效。

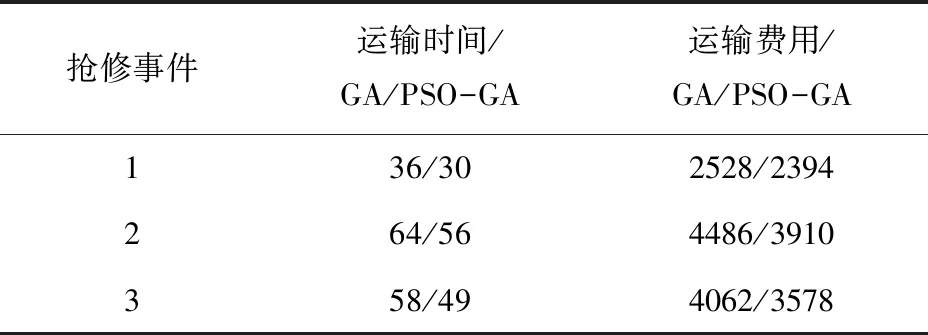
表5 算法对比结果

由图3可知，PSO-GA算法比GA算法收敛速度更快，能得到更优解。经大量实验验证，通过该模型算法获得的最优调度方案优于由遗传算法获得的调度方案，所用时间和费用较少，平均减少大约10%，效果较好。

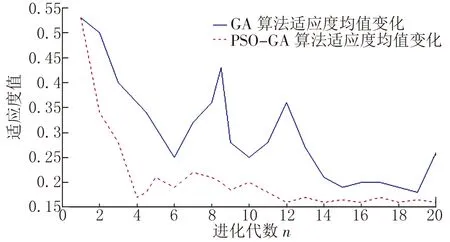
图3 进化20代的种群平均适应度值比较

4 结语

高效的输电线路应急抢修物资调度模型及算法能够指导抢修人员和物资到达故障点，缩短抢修时间，减轻劳动强度，提高工作效率，节约开支。有运输能力约束的时间和费用最优的应急资源调度模型更符合输电线路应急抢修实际，改进的混合粒子群遗传算法更优于经典遗传算法，收敛速度快，减少了调度时间和费用。新的智能算法不断涌现，未来可进一步探索应用于应急抢修物资调度的新算法的结合与优化。