思维可视:让学生的数学思维在场
唐永玲
在数学学习中,思维发展比知识获得更重要,思维品质是学生核心素养培养的关键纬度。让思维可视,就是以发展学生的思维为教学着力点,想方设法把学生的思考方法和思考路径呈现出来,使其清晰可见。有研究表明,被可视化的思维可以有效提高信息加工及信息传递的效能。在数学教学中,教师要想方设法将学生学习过程中的思维过程以看得见的形式呈现出来,促进学生更深度地投入学习,同时有助于教师及时了解学生的思维水平,更好地调控教学进程。
1.引导学生把心中的数学“写”下来,让思维可视
其一,用算式记录思维过程,感悟计算算理。在计算教学中,常有学生把计算过程完整地说出来,但几个学生会了并不代表全班学生都已经掌握了计算算理。例如,教学“45+27”时,为了让每个学生都有机会经历参与学习和提升思维的过程,教师提出如下要求:你会计算45+27 吗?把你的计算过程写在本子上,比一比,看谁的方法多。然后并联呈现学生的多种算法,并让学生观察这几种算法:你能看懂这些方法是怎样计算45+27 的吗?先看一看,再跟同桌说一说每种方法分别是怎样计算的。如此,每个学生都经历了独立思考的过程之后,再去观察、辨别、分析,与自己的思维进行碰撞,感受各种方法的优劣。在这个过程中,每个学生都在思考、感悟和成长。
其二,用符号记录思维过程,化抽象为形象。文字具有抽象性,符号比文字更加形象直观。小学生喜欢看简单形象的事物,符号有时候可以让数学变得更加浅显易懂。例如,有这样一个数学问题:3 支铅笔和2 支圆珠笔的价钱一共是12 元,5 支铅笔和2 支圆珠笔一共16 元。那么圆珠笔和铅笔的单价各是多少元?教师教学时可以引导学生用简单的符号(如下页图1)来形象地表示两种笔:为什么16 元会比12 元多呢?看符号很容易得出:因为多买了2 支铅笔,所以多出的4 元就是2 支铅笔的价钱。在解决问题时把文字转换成简洁的符号,可以将学生的思维过程清晰地展现出来,从而促进学生主动学习。
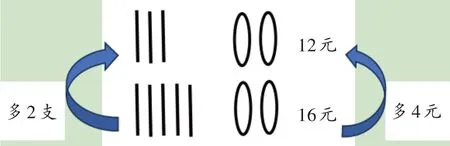
(图1)
2.引导学生把心中的数学“画”出来,让思维可视
小学生的思维以具体形象思维为主,并逐步向抽象思维发展。“一图胜千言”,以视觉化表征的知识,能在很大程度上减轻信息负载,便于信息加工。线段图、示意图、流程图等比较形象、直观、具体,不仅可以充分外显学生的思维过程,还能促进学生学会思考问题、解决问题。
其一,数形结合,让数的内涵意义清晰可见。数学家华罗庚说过:“数缺形时少直觉,形少数时难入微。数形结合百般好,隔裂分家万事非。”很好地阐释了数形结合的优势。如教学“分数”,在比较分数的大小时,有些学生始终不理解为什么二分之一大于四分之一,教师可以引导他们画图来分别表示出这两个分数,从分数的意义上去辨别比较,从而便于学生理解。
其二,数形结合,让数量关系跃然纸上。数形结合的思想方法在数学学习中一直受到广泛应用。如在解决“和倍问题”“差倍问题”“和差问题”“拼接、分割图形的周长”“面积变化问题”等典型的数学问题时,通过画线段图、示意图可以清晰直观地表示出各个数量之间的关系,从而使学生更好地找到解决问题的思路和方法。如在教学“面积变化的问题”时,教师出示如图2 所示的问题,并引导学生思考:怎样才能更好更快地解决问题呢?学生不约而同想到了画图。画图之后,教师引导学生思考:你觉得图有没有作用呢?学生的体会深刻。其实,画图的过程就是运用直观之“形”表征抽象之“数”的过程,就是学生提炼信息、加工信息、梳理思路的过程,是学生的数学学习逐步数学化的过程,体现的是学生对用文字表述的数量关系的另一种“语言”表达,有助于学生理解数学概念、解决数学问题,培养和提升思维品质和学习能力。

(图2)
其三,数形结合,让数学之理一目了然。数学是有趣的,数学领域中蕴含着丰富的规律;数学是神秘的,数学知识里深藏着各种美;数学是奇妙的,数学学习中充满着智慧。数形结合有时能巧妙地解决数学难题,让数学之理显而易见,让学生体会到数学的趣味。如在探索“分数计算的规律”时,结合图形来引导学生解决分数计算的问题(如图3),学生很容易就能理解其中的算理。
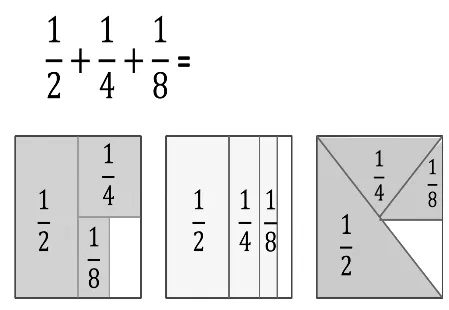
(图3)
总之,可以清晰地呈现学生思维过程的方法都可以称为“让思维可视”。让学生的思维可视,教师教学时要充分外显学生的思维过程,促使学生的自主学习、有效学习、深度学习真正发生。

