深埋高地应力隧道勘察期岩爆烈度概率分级预测

刘威军，范俊奇，李天斌，郭 鹏，曾 鹏，巨广宏

（1.成都理工大学环境与土木工程学院，四川 成都 610059；2.中国电建集团西北勘测设计研究院有限公司，陕西 西安 710000；3.军事科学院国防工程研究院，河南 洛阳 471023）

一般认为岩爆是在高地应力作用下硬脆性的储能岩体在开挖过程中能量突然释放而产生爆裂、剥落、弹射等现象的一种动力失稳地质灾害。自1738年在英国南史塔夫煤田莱比锡煤矿坑道中首次发生岩爆现象以来[1]，高地应力硬岩地下工程岩爆灾害导致人员伤亡、支护破坏和工期延误的情况时有发生。据统计，从2001—2007年中国矿区共发生13 000起岩爆事故，伤亡人数超16 000 人[2]。岩爆灾害由于其突发性高、不确定性强及破坏性显著等特点，至今仍是困扰地下工程安全施工的难题[3]。随着我国隧道建设的高速发展，特别是西南山区铁路和高速公路的开工建设，必将面临更加复杂的地质环境。因此，岩爆的有效判识和预测已成为制约西南地区隧道工程建设的重要技术瓶颈。

岩爆预测可分别实施于隧道勘察阶段和施工阶段。相比于传统的施工阶段岩爆预测，勘察阶段预测的主要目的是为工程选线提供技术支撑，从而尽量规避高烈度岩爆对施工的影响，同时为隧道开挖和岩爆控制措施设计（如超前应力释放、高压注水和柔性防护手段）提供数据支撑[4]。

国内外学者就岩爆预测问题进行了广泛研究，取得了丰硕成果。其中许多学者基于高储能体以及高地应力提出了岩爆发生的经验判据。如Russense[5]就挪威隧道提出了洞壁最大切向应力与岩石单轴抗压强度之比的Russense 判据；Kidybinski[6]提出了岩爆倾向性指数；陶振宇等[7]总结国内工程提出了岩石单轴抗压强度与原岩最大主应力之比的陶振宇判据；以及徐林生等[8]提出的二郎山判据等。随着应用数学、深度学习等人工智能方法的发展，许多学者提出了不同的岩爆智能预测方法。冯夏庭[9]应用神经网络进行岩爆风险评估，建立了地下洞室岩爆风险估计的自适应模型；冯夏庭等[10]建立了基于支持向量机的岩爆预测预警模型，通过选取影响岩爆的主要因素，应用典型案例对模型进行训练，并用于实际工程进行岩爆预测，预测结果和实际情况较一致；李天斌等[11]、何怡帆等[12]提出岩爆预测的综合集成方法，将地质分析预测、应力强度比、层次-模糊评判法和神经网络法综合考虑，形成了定性和定量相结合的理论方法；刘磊磊等[13]、徐琛等[14]通过层次分析法和熵权法相结合的组合赋权法来评价各个指标的影响程度，选取不同的评价指标，建立了理想点法岩爆预测预报模型；董源等[15]从岩石力学性质、围岩条件等方面选取15 个岩爆评估指标，采用类似的方法建立了岩爆云模型，其判别结果与实际相符；王迎超等[16]选取洞壁最大切向应力比单轴抗压强度（σθ/σc）、单轴抗压强度比单轴抗拉强度（σc/σt）、岩爆倾向性指数（Wet）和岩石脆性指数（Is）作为岩爆预测的指标，用德尔菲法确定各评价指标的权值，建立了岩爆风险正态云的评判模型。同时，极限学习机、逻辑回归和支持向量机等人工智能方法也被引入岩爆灾害预测研究中，获得了较好的效果[17-19]。这些方法建立在众多研究因素与岩爆风险的复杂非线性关系之上，减少了人为干预，极大地推动了岩爆预测技术的发展。

然而，针对我国西南高山峡谷区交通干线工程隧道勘察期的实际应用需求，上述方法还存在一些不足。首先，传统经验模型使用的预测指标较为单一，预测精度比较有限，其工程适用性受其模型数据库来源影响较大。其次，现有岩爆智能预测方法大多针对隧道施工期，很多模型的预测指标只能在隧道开挖后才能准确获取，如岩爆倾向性指数、岩石脆性指数等。另外，部分模型理论性比较强，在一定程度上忽略了预测指标的可获取性，给实际工程应用带来困难。

因此，本文针对西南山区交通工程隧道勘察设计的需求，结合国内外现有岩爆预测方法，有针对性地选取预测指标，并对案例数据进行分析和甄别，利用贝叶斯网络模型构建不完备数据条件下隧道勘察期岩爆智能预测模型，并在雅安—叶城高速跑马山1 号隧道开展工程应用，为工程建设提供重要技术支撑。

1 预测指标选取与数据库构建

1.1 预测指标选取与参数获取

考虑工程勘察阶段岩爆预测指标数据的可获取性，通过与地质、勘察、隧道等行业的专家深入讨论，确定了选用岩石强度、地应力、地质构造和围岩级别4 个关键指标作为岩爆预测因子。

（1）岩石强度

岩爆发生的必要条件是岩体存储较大的弹性应变能，而其储能能力与岩石强度密切相关，二者呈正相关关系。岩石强度可通过隧道勘察阶段对隧道轴线进行钻孔取芯，开展室内单轴抗压强度（Rc）测试获得。在难以取芯试验的隧道轴线部位，亦可基于勘察期工程地质资料推测拟预测隧道断面地层岩性，从而判断其对应的岩石强度分类级别。

（2）地应力

高地应力区域硬岩隧道工程开挖过程中，洞壁切向应力增大、径向应力减小，引起明显的围岩应力分异现象，导致围岩存储能量增加，引起围岩脆性破坏[21]。大量国内外研究成果表明，高地应力是岩爆发生的必备因素之一；地应力越高，发生岩爆的可能性越大。

地应力随埋深增加而增大，二者呈近似线性关系[22]。地应力测量是获取隧道地应力场最直接、最可靠的方法[22-25]。但考虑到工程勘察阶段地应力测试孔间距大、数据非常有限，本文采用杨树新等[26]提出的我国青藏地块水平地应力修正公式（σ= 0.029 2H+5.185）预测隧道地应力值（H为隧道埋深）。

（3）地质构造

隧道工程所处的区域构造部位对岩爆的发生具有重要的影响。岩爆形成必须具备的条件之一是岩体处于高应力集中状态，而构造应力场随地壳运动和地质构造的变化而变化，如大型断裂带、褶皱核部、断层附近等一般属于构造应力集中区[20]。因此，明确隧道工程所处地质构造部位对岩爆预测起着至关重要的作用。

区域构造主要考虑无地质构造、褶皱核部、断层附近、褶皱两翼及断层破碎带等情况。地质构造的获取可将隧道工程所处位置的区域地质图以经纬度坐标为标准投影到ArcGIS 上，沿线路依次读取目标里程的地质构造情况并做相应记录。

（4）围岩级别

岩体的结构类型及其特性是发生岩爆的物质基础。岩体结构完整且岩体干燥情况下更有利于储存弹性应变能。该类岩体围岩级别大多为Ⅰ、Ⅱ、Ⅲ级。而围岩级别反映岩体结构类型及性能的同时，也可以反映围岩总体质量的好坏，因此围岩级别可作为影响岩爆发生的重要因素之一。

在勘察阶段围岩级别主要根据地质勘察资料获取。通过分析、调研区域地质资料，研究地下工程所在区域宏观地质条件，对目标区域地层结构、地质构造、水文地质条件等综合分析、判定，确定隧址区围岩级别。一般而言，该指标可从隧道勘察报告中获取。

1.2 数据库构建

本文依据李天斌等[27]提出的岩爆烈度分级方案，基于声响、运动、失效、波及深度等特征，将岩爆烈度分为无岩爆、轻微岩爆、中等岩爆和强烈岩爆等4 个级别。基于前述预测指标，即可确定岩爆案例数据库所含信息。每条案例信息包括地质构造、地应力、围岩级别、岩石强度和岩爆烈度等5 个关键信息。基于研究团队在西南地区典型高地应力硬岩隧道十余年的积累，通过对锦屏二级水电站隧洞、二郎山隧道、秦岭隧道、福堂隧道、西康铁路秦岭隧道等11 条典型隧道的详细统计分析，获得498 组岩爆案例，如表1所示。其中，无岩爆57 组，轻微岩爆173 组，中等岩爆145 组，强烈岩爆123 组。

表1 岩爆案例数据来源统计及岩爆烈度的分布Table 1 Statistics of rockburst cases and the distribution of rockburst intensity

对数据库中各岩爆案例烈度统计发现，除无岩爆案例相对较少以外，其他烈度案例个数分布较为均匀。图1 展示了4 个预测指标的直方图和累计分布函数。统计结果显示，该数据库包含了4 个预测指标的大部分数据范围。另外需要指出的是，后文岩爆预测只针对该范围内数据。随着未来新数据的加入和范围的扩展，该方法将具有更普遍的适用性。

图1 预测指标统计信息Fig.1 Statistical information of prediction factors

1.3 数据处理

在岩爆数据收集的过程中，由于复杂施工环境、仪器精准度和人为操作等影响，收集到的数据中会存在一些异常值或离群值。数据预处理是数据分析过程中非常重要的一步，正确的数据将保证分析结论的正确。箱型图可以发现数据中的异常值/离群值，其异常值识别标准为小于Q1–1.5IQR和大于Q3+1.5IQR，其中Q1为下四分位数、Q3为上四分位数、IQR为四分位距（Q3–Q1）。本文利用箱型图方法对地应力和岩石强度2 个连续变量进行异常值检测，可以看出2 个指标均存在异常值（图2 中黑色轮廓*代表极端异常值，黑色轮廓〇代表温和异常值），需对所有异常值进行处理。通过查看箱型图中异常值的样本序号，删除该条样本数据，再用删除后剩余的数据构造有效案例数据库，如图2 所示。最终剔除25 组异常值，保留473 组有效岩爆案例数据。

图2 预测指标异常值检测与剔除Fig.2 Detection and elimination of outliers

2 贝叶斯网络原理及模型构建

2.1 贝叶斯网络原理

贝叶斯网络是一种以有向无环图的形式处理一组变量之间概率关系的图形模型[28]。网络中的节点表示随机变量。如果2 个节点有直接的因果关系（即变量之间相互依赖），其间将通过箭头连接；同样，2 个变量之间缺少箭头表示二者条件独立。

贝叶斯网络建模的第一步是确定网络拓扑结构，以便仔细考虑将用于作为输入变量之间的条件独立和依赖关系。一旦确定了贝叶斯网络拓扑结构，就需要定义变量间关系强度，即一个变量相对于另一个变量的条件概率。对于离散变量而言，使用条件概率表来量化各节点变量间条件概率[29]。

朴素贝叶斯是一种简单的贝叶斯网络结构，由父节点（1 个）和子节点（多个）组成，并且假设子节点之间相互独立。国内外研究表明，朴素贝叶斯相对于其他贝叶斯网络，其结构简单且学习、推理效率高，得到大量试验和研究的广泛应用[30]。因此，根据本文搜集到的岩爆数据，利用Pearson 函数对4 个预测指标变量进行相关性分析，以推断条件独立假设是否充分，结果如表2 所示。根据表中数据得出4 个指标两两之间相关性系数绝对值均小于0.6，本文为简便起见假设4 个节点变量具有统计独立性。

表2 预测变量间相关系数Table 2 Correlation coefficients of prediction factors

针对本文岩爆预测研究实际情况，根据预测指标相关性结果，采用基于专家建议确定节点以及变量间依赖关系的方法来构建勘察期岩爆预测朴素贝叶斯网络模型拓扑结构。

2.2 连续参数离散化

用于勘察阶段贝叶斯网络模型的预测指标中，地质构造和围岩级别为离散参数，地应力和岩石强度为连续参数。鉴于贝叶斯网络处理连续数据的实际能力有限[28]，本文依据李天斌等[26]提出的地质分析法岩爆预测思想，基于实际情况将地应力和岩石强度处理为离散参数。同时，为方便建模，本文对指标离散化区间进行赋值，如岩爆烈度对应的无岩爆、轻微岩爆、中等岩爆、强烈岩爆4 个级别分别用数字0、1、2、3 来替代离散结果，其他指标赋值方式见表3。

表3 预测指标节点离散化取值Table 3 Threshold values for prediction factor discretization

2.3 贝叶斯网络模型构建与验证

贝叶斯网络参数学习是在图3 定义的拓扑结构的基础上，根据岩爆数据库中473 条案例数据确定条件概率表的过程。由于该数据库中存在缺失值，期望最大算法（EM）为数据缺失条件下贝叶斯网络的参数估计提供了有效的解决方案。通过期望步骤发现所期望参数的完整数据，利用最大化步骤重新估计参数，从而得到不完整数据集中缺失数据的最大似然估计值。

图3 岩爆烈度概率预测贝叶斯网络模型Fig.3 Bayesian network model for probabilistic prediction of rockburst intensity

在用EM 算法获得条件概率表后，即可使用信念更新计算给定证据（一组新的观测数据）的后验概率分布[31]。对于岩爆烈度预测分析，其目的是在得到预测指标的情况下计算岩爆发生的后验概率，其中相关指标可以是一组关于输入参数向量不完整的观测结果。在本研究中，采用广泛使用的Junction Tree（JT）算法进行信念更新。

为检验模型的准确性和有效性，需要对所构建的勘察阶段岩爆烈度分级概率预测贝叶斯网络模型进行验证。本文选用十折交叉验证方法（图4），将473组岩爆模型训练样本分成10 组，依次将每一组轮流作为验证集，其余9 组作为训练集，交叉验证重复10＞次。每个模型准确率和混淆矩阵见表4。10 个模型中准确率最高为95.83%，最低为73.17%，平均值为84.47%。该准确率平均值可作为模型的性能度量。值得注意的是，每个预测错误的岩爆烈度并没有出现越级现象，即假设实际结果为中等岩爆，错误预测结果为强烈或轻微岩爆，未出现无岩爆这种越级错误预测结果，这对实际工程应用而言非常重要。

图4 十折交叉验证流程图Fig.4 Flow chart of 10-fold cross validation

表4 模型十折交叉验证的准确率和混淆矩阵Table 4 Accuracy and confusion matrix of the model for 10-fold cross-validation

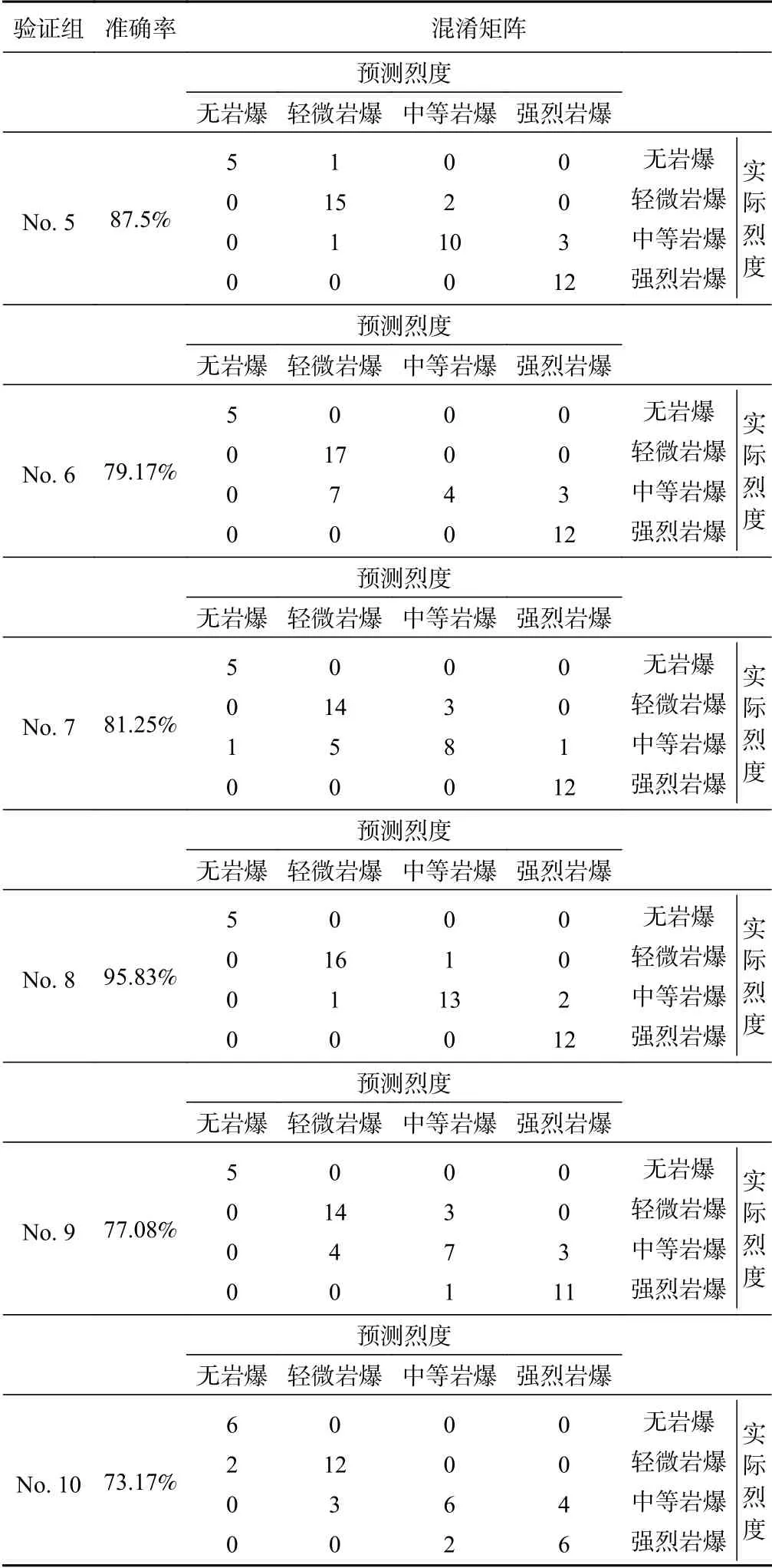
表4 模型十折交叉验证的准确率和混淆矩阵（续表4）

3 跑马山1 号隧道工程应用

跑马山1 号隧道位于四川省康定市东北部，是雅安—叶城高速康定过境段的重要组成部分。隧道全长8 780 m，最大埋深1 250 m。全隧超过85%的洞段为花岗岩，岩体较完整-完整，主要为Ⅱ、Ⅲ、IV、Ⅴ级围岩，具备发生岩爆的地质环境条件。

基于该隧道勘察设计报告，结合前节所述方法确定隧道勘察阶段28 个典型断面围岩级别、岩石强度等4 个预测指标信息，如表5 所示。使用本文建立的隧道勘察期岩爆烈度概率分级预测贝叶斯网络模型对这28 个断面岩爆灾害进行预测，结果如表5 所示。

表5 跑马山1 号隧道岩爆基础信息与烈度预测结果Table 5 Basic information of rockburst and the predicted results of Paomashan No.1 tunnel

跑马山1 号隧道在实际施工过程中遭遇了一系列岩爆灾害。根据对现场岩爆现象的多次深入调查，获得28 个断面的岩爆现象实际情况（表5）。根据李天斌等[26]提出的岩爆机理与地质力学模式判别方法，对岩爆发育特征进行分析研究，总结出跑马山1 号隧道岩爆发育特征如下：

（1）岩爆发生部位大多为围岩完整性较好、块状结构的岩体中，围岩稳定、较坚硬、干燥、裂隙不发育；

（2）岩爆的破坏模式主要是以片/层状剥落和穹状爆裂为主，少数为弯曲鼓折破裂，如图5（a）（b）（c）所示；

图5 跑马山1 号隧道岩爆破坏模式Fig.5 Failure modes of rockburst in Paomashan No.1 tunnel

（3）岩爆破坏面多以平整破裂面、阶梯状破裂面以及穹状破裂面为主，少数为贝壳状破裂面；

（4）岩爆的破坏性质多以张性破坏和张剪性破坏为主，运动特征主要以松脱、剥落为主；

（5）岩爆发生烈度主要是轻微岩爆和中等岩爆。

对比分析预测结果显示，28 次岩爆预测中有24 次正确、4 次错误，准确率高达85.71%。其中2 组错误预测中，现场判别为轻微-中等岩爆，而本文模型预测为轻微岩爆。因此，本文所构建的隧道勘察期岩爆预测模型准确率优良，能满足实际工程应用的需求。

通过具体数据对比分析发现，例如桩号ZK2+401，由于岩石强度从较坚硬岩变为坚硬岩，轻微岩爆的概率从68.7%下降至2.88%，中等岩爆的概率从31.3%上升至91.8%，强烈岩爆的概率从0%上升至5.32%。该结果表明，随着岩石强度的增加，岩爆烈度也逐渐提高。该结果符合实际情况，同时也在一定程度上证明了预测模型的合理性和适用性。同时，值得指出的是，本文模型在跑马山隧道的验证结果并不能完全代表该模型在该区域隧道岩爆预测中的适用性和准确性。因为跑马山隧道地质构造相对简单，且28 个预测案例中没有包含强烈岩爆灾害。

4 结论

（1）通过总结归纳我国西南地区地下工程岩爆发生案例，构建了一个包含498 条案例的岩爆数据库。针对现场调研数据存在错误的可能性，利用箱型图方法对数据库进行去噪处理，最终保留473 条案例数据，有效提高了数据质量。

（2）采用期望最大化算法对473 组有效岩爆案例进行参数学习；使用Junction Tree 算法对有关输入参数变化时岩爆烈度进行信念更新，构建了隧道勘察期岩爆烈度概率分级预测贝叶斯网络模型。通过十折交叉验证获得模型准确率高达84.47%，表明该模型具有较好的预测精度。

（3）将岩爆预测模型应用于雅安—叶城高速跑马山1 号隧道，对现场28 个开挖断面岩爆灾害烈度进行概率分级预测。预测结果与实际开挖后岩爆灾害观测结果高度吻合，模型准确率高达85.71%。