微分方程初值问题的MATLAB/Simulink求解

付志粉，马建立，李 洋，王 兵

(安徽理工大学力学与光电物理学院，安徽淮南 232001)

0 引言

微分方程的初值问题求解是自然科学、工程技术和经济生活等领域经常遇到的问题，此类问题的求解有些可以得到解析解，有些则不能，此时利用数值法求解显得尤为重要.数值法求解微分方程的基本思想是离散化，求解方法分两类，即单步法(如Euler法及Runge-Kutta法等)和多步法(如Adams法)[1-2]，具体的求解过程颇为繁杂，常常需要用到MATLAB或C语言编写代码，这给此类方程的求解带来诸多不便.Simulink是MathsWorks公司基于MATLAB软件平台开发的可用于对动态系统进行建模、仿真和分析的工具包.在MATLAB环境中利用Simulink提供的可视化编程界面，用户利用其内置的各种功能化模块编写程序，无需进行繁杂的代码编写，就可搭建出复杂的数学模型并对其进行仿真求解.鉴于此，本文使用MATLAB/Simulink工具箱对一阶微分方程(组)、二阶微分方程及高阶微分方程的初值问题进行建模、仿真和图解，以期为该类问题的数值求解提供参考.

1 微分方程初值问题的MATLAB/Simulink求解过程

使用MATLAB/Simulink工具箱求解微分方程的初值问题可分为以下过程：

(1)启动Simulink工具箱，选择相关模块.在MATLAB命令窗口中输入“Simulink”或者单击MATLAB工具栏中的Simulink图标，即可打开Simulink窗口.单击该窗口“File”菜单中“new”选项下的“Blank Model”命令，新建一空白模型文件.根据所求解微分方程左右两边各项的特点从模块库中选择相应的模块添加至新建的空白模型文件中.微分方程求解时常用的模块有积分器Integrator模块、加法器Add模块、增益Gain模块、乘法器Divide/Dot Product模块及用来显示求解结果的示波器Scope模块等.

(2)搭建微分方程模型.将(1)中所选定的模块放置好后，按照一定的顺序连接起来，构成Simulink仿真模型.

(3)设置仿真参数.在积分器模块属性中设置微分方程的初始条件，单击工具栏的“Model Configuration Parameters”选项后在打开的页面中设置仿真起始和终止时间及具体的方程求解算法类型等.

(4)运行程序，求解方程.单击工具栏中的程序运行按钮“Run”，待仿真结束后单击示波器模块，即可得到微分方程解的图示.

2 MATLAB/Simulink数值求解微分方程算例

2.1 一阶微分方程初值问题的MATLAB/Simulink求解

一阶微分方程的求解方法有分离变量法、全微分法、常数变易法、特征方程法及待定系数法等[3].有关一阶微分方程初值问题的求解通常是先采用前述方法求出方程的通解，然后将初值代入通解中确定常数C，最终得到满足初值条件的一阶微分方程的解.这样的方程求解过程步骤多、计算量大且易出错.采用MATLAB/Simulink工具箱求解则可以将复杂、费时的方程求解过程变得简单、直观、省时.如求解方程：

y′=y-2x/y

(1)

其中y(0)=1，0≤x≤10的解.

所搭建的Simulink模型框图如图1(a)所示.其中积分器Integrator的输入信号为y′，输出信号为y.将时钟信号源Clock模块提供的信号x和积分器Integrator模块的输出信号y分别接入除法器Divide模块的输入端，经过除法器Divide模块后的信号即为x/y，此信号经过增益Gain模块扩大-2倍后接入加法器Add模块的下输入端口.加法器Add的上输入端口引入信号y，下输入端口为信号-2x/y，加法器Add模块的输入信号即为y-2x/y，其输出信号为y′(积分器Integrator模块的输入信号).双击积分器Integrator模块在弹出的对话框中设置初值条件，在工具栏中设置仿真时间为10 s(此即设置x的取值范围).示波器Scope模块是用来图示信号y随x的变化情况的.设置好参数后点击工具栏中的程序运行按钮“Run”后，点击示波器即可得到方程的求解结果，如图1(b)所示.

图1 方程(1)的Simulink求解模型框图及解的结果Fig.1 Simulink solution model block diagram and solution results of equation (1)

3.2 一阶微分方程组初值问题的MATLAB/Simulink求解

1963年，美国气象学家Lorenz在研究大气对流时建立了著名的Lorenz方程，该方程在混沌和可预报性方面有广泛的研究.Lorenz方程为一个三元一阶微分方程组，其形式为：

(2)

其中α，β，γ为固定值，t为时间，对于给定的初值x1(0)、x2(0)及x3(0)，可利用MATLAB/Simulink工具箱求解该方程.为便于与文献[4]中的结果比较，此处取α=8/3，β=10，γ=28，初值x1(0)=x2(0)=0，x3(0)=10-10.所搭建的仿真模型如图2(a)所示，采用三接口示波器Scope模块，自上而下依次接入变量x1(t),x2(t)及x3(t),方程的求解结果即变量的时间响应见图2(b).需要注意的是加法器Add3模块采用的是3输入端口的，各输入端口的“+”“-”可根据需要设置，自上而下该加法器的输入量依次为x3(t)，28x2(t)及x1(t)x2(t).三个To Workspace模块将积分器输出的量x1(t),x2(t)及x3(t)分别写入MATLAB的工作空间中.图2(c)示出的是在命令窗口中使用plot3函数绘制的变量x1,x2及x3的三维相空间图.可以看到采用Simulink求解该方程所得的结果与文献[4]中采用代码编程求解的结果一致，但采用Simulink求解要简单、直观一些.

图2 Lorenz模型的Simulink求解模型框图及解的结果Fig.2 Lorenz model Simulink solution model block diagram and solution results

3.3 二阶微分方程初值问题的MATLAB/Simulink求解

1927年荷兰科学家Balthasarvan der Pol在研究LC回路电子管振荡器时建立了一个二阶微分方程(简称van der Pol方程)，该微分方程在电学和力学中有着广泛的应用.van der Pol方程的表达式如下：

y″+μ(y2-1)y′+y=0

(3)

其中μ>0为标量参数，此方程在数学上无法精确求解.下面采用MATLAB/Simulink工具箱数值求解该方程，令方程初始条件为y(0)=-0.2，y′(0)=-0.7，其中μ取2.搭建的Simulink模型框图如图3(a)所示，框图中积分器integrator1模块的输入信号为y″，输出信号(积分器integrator2模块的输入信号)为y′，示波器Scope模块用来显示y及y′随时间t的变化，双综示波器XY Graph模块显示的是y′(t)及y(t)在相平面的运动情况.初值条件及μ的取值可在积分器integrator1、integrator2及增益Gain模块中修改.仿真时间设为20 s，仿真结果如图3(b)及3(c)所示.与文献[5]中采用MATLAB语言编程所得结果比较后发现，两者所得结果一致，但Simulink采用模块化的编程方式编写的程序易于理解，可显示信息的流动，且程序调试、修改方便，具有直观、高效的特点.

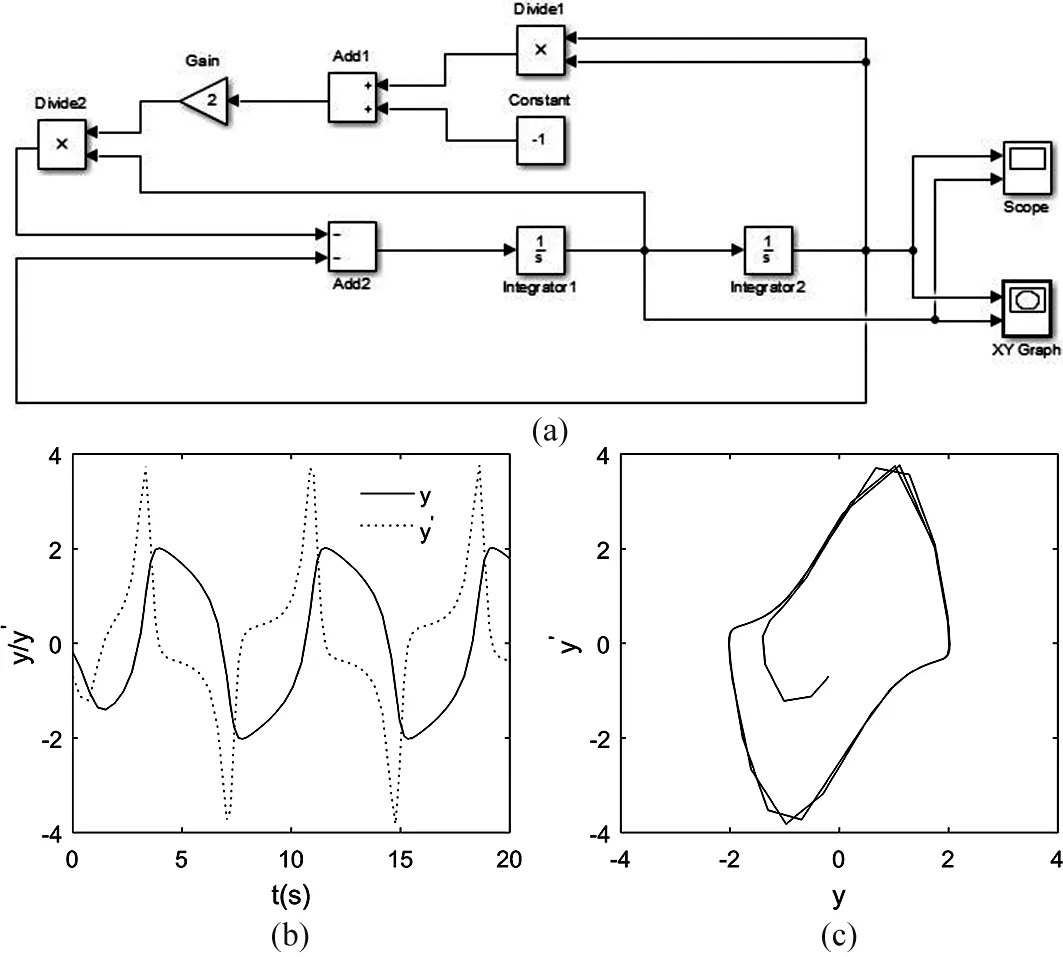
图3 van der Pol方程的Simulink求解模型框图及解的结果Fig.3 Simulink solution model block diagram of Van der Pol equation and solution results

3.4 高阶微分方程初值问题的MATLAB/Simulink求解

对于高阶微分方程的求解，通常采用降阶法，即利用变换将高阶方程化为较低阶的方程后进行求解，此过程往往较为复杂.采用MATLAB/Simulink工具箱数值求解，可化繁为简，化抽象为具体.如求解四阶非刚性微分方程：

y(4)+2costy″+sinty=7e-t

(4)

其中y(0)=y′(0)=y″(0)=1,y‴(0)=0.搭建的Simulink模型框图如图4(a)所示，其中积分器integrator1到integrator4模块的左端分别为输入信号y(4)，y‴，y″及y′，2cost和sint分别由正弦波信号发生器Sine Wave1及Sine Wave2模块产生，加法器模块自上而下输入的信号分别为7e-t，sinty及2costy″.在各积分器模块中设置初值条件，仿真时间设为100 s，运行后的结果见图4(b).可以看到此结果与文献[6]采用MATLAB语言编写代码求解的结果一致.相比较而言，采用Simulink求解，数学思想清晰，比较符合人们的思维习惯.

图4 四阶非线性微分方程的Simulink求解模型框图及解的结果Fig.4 Fourth-order nonlinear differential equations in Simulink solution model block diagram andsolution results

3 结论

本文结合具体算例，利用MATLAB/Simulink对带有初值条件的一阶微分方程(组)、二阶微分方程及高阶微分方程进行了求解.结果表明：采用Simulink提供的可视化编程环境能够方便地对带有初值问题的微分方程进行求解和结果可视化，该方法程序直观、简洁，求解速度快，不失为一种求解微分方程初值问题数值解的有效方法.