基于改进粒子群算法的恒力输出器的力控制优化
王君, 任前程, 杨铭全, 汪泉, 曾顺麒
(湖北工业大学机械工程学院,湖北武汉 430068)
0 前言
抛光和打磨等表面精加工在制造业中发挥着重要作用,这些操作不仅为了外表美观,而且主要是为获得指定的表面粗糙度。通常打磨抛光作业是由工人手动执行的,劳动成本高,效率低,工作环境恶劣且依赖于工人的技能熟练度[1-3]。因此,需要一种高效的打磨抛光方式代替手工打磨。工业机器人具有成本低、灵活性高、可编程性强和适合强度工作等优势,因此工业机器人与打磨工艺相结合成为主要研究方向[4-5]。
在表面精加工应用情况下,控制接触力以确保处理过的零件具有相同的质量至关重要。因此,工业机器人需要具有精确的力感知和力控制能力。很多学者对此问题进行了大量研究。FANAEI 和FARROKHI[6]在力/位混合控制的基础上加上了模糊理论,将其应用到需要工具与零件之间保持恒定摩擦力的工况中。肖露和秦红玲[7]为了解决加工过程中由于磨损造成的加工精度下降问题,提出了利用模糊控制与传统PID控制相结合的方法控制系统输出恒定的磨削力。黄婷等人[8]采用非线性PD控制,提高了被动柔顺装置的力/位混合控制精度。PEI等[9]通过结合反向传播(BP)神经网络和Smith 预测器的改进PID控制方法,缩短最大超调量和调整时间。
为提高力控制的控制性能,将粒子群算法引入到模糊PID控制中,并加入混沌策略对粒子群算法进行改进。利用MATLAB进行对比仿真分析,并在搭建的恒力打磨平台进行实验,验证该方法的有效性。
1 恒力输出器建模
1.1 恒力输出器结构及工作原理
恒力输出器模型如图1所示。其工作原理:打磨抛光作业时,若打磨头与待加工工件接触产生的接触力大于预设定的恒力值,出气口打开,缓冲气缸向上法兰盘方向移动,直至接触力等于预设定恒力。同样,当接触力小于设置的恒力时,进气口打开,恒力输出器的缓冲气缸向下法兰盘方向移动,直至接触力等于预设定恒力。恒力输出器内部还包含电子调压阀、电磁阀、气缸磁性开关。电子调压阀的作用是控制缓冲气缸内的气压,电磁阀控制缓冲气缸的运动方向,气缸磁性接近开关用于位置的监测,从而得到执行器末端的位置参数。
1.2 模型建立
1.2.1 受力平衡模型
图2所示为恒力输出器简化的受力示意图。
根据牛顿第二定律有:
(1)
式中:F为恒力输出器的输出力;f为活塞与气缸的摩擦力;c为黏性阻尼;p0为缓冲气缸上腔气压;A0为活塞的有效面积;x为缓冲气缸的轴向位移;m为整体质量。
1.2.2 气体流量模型
电子调压阀的流量公式采用圣维南流量公式[10]表示:
(2)
式中:Ac为电子调压阀的进气阀口面积;pic为电子调压阀进气口压力;poc为电子调压阀出气口压力;T为绝对温度;k为比热容;R为理想气体常数;Cf为流量系数。
根据式(2)可知流入调压阀的气体流量与进气阀口开度有效面积有关。依据电气比例阀的特点,阀口开度与调压阀的控制电压U有关,而电压U会影响调压阀出口的压力poc,所以比例调压阀的流量方程是关于输入电压U和比例调压阀出口压力poc的函数。则此气体流量变化模型为
Δq=K1ΔU+K2Δpoc
(3)
气体通过电子调压阀后,需要通过长度为L的管道到达缓冲气缸。忽略其他因素的影响,依据Anderson理论,得到式(4),并根据式(4)得到缓冲气缸气体流量变换模型式(5)。
(4)
Δq=K3(Δpi-Δpo)
(5)
式中:pi为管道进气端压力;ρ为气体密度;D为管道直径;μ为气体的黏性系数;A为管道横截面处的有效面积。
假设进入缓冲气缸中的气体为理想气体,气体持续不断地进入缓冲气缸,并根据气态方程(6),可推导出缓冲气缸上下两腔的气体流量qn关于气缸内气体质量变化率的方程(7):
pinsideV=nRTo
(6)
(7)
式中:pinside为气缸内气体压力;V为气缸内气体体积;n为气体物质的量;To为进入缓冲气缸后气体温度。
假设气体随着缓冲气缸运动时不会和外部产生热交换,则温度初值Ts与运动过后的温度To两者关系能够用式(8)表示,两边对时间求导得到式(9)并代入式(7),由于整个缓冲气缸在自身法线方向只存在微小的改变,为简化模型,此方向可以忽略不计,更新后缓冲气缸中的气体质量与流量的模型为式(10):
(8)
(9)
(10)
1.3 恒力输出器传递函数建立
将上面分析计算得到的式(3)(5)(10)进行拉普拉斯变换,分别得到式(11)(12)(13):
Q(s)=K1U(s)+K2Poc(s)
(11)
Q(s)=K3[Pi(s)-Po(s)]
(12)
(13)
由于气体由比例阀的出口进入管道的入口,管道入口的压力等于比例阀出口的压力,即Poc=Pi。联立式(11)—(13)可得
(14)
将恒力输出器的受力方程(1)进行拉普拉斯变换得到式(15),为简化模型将摩擦力忽略不计。
ms2X(s)+csX(s)+F(s)=Po(s)Ao
(15)
连接在下法兰盘末端的打磨工具与工件接触时,由于反作用力的作用使得恒力输出器产生x的移动,整体的等效刚度为K4,反作用力作拉普拉斯变换得到:
F(s)=K4X(s)
(16)
联立式(15)和(16)得到:
(17)
将式(14)与式(17)相乘可得恒力输出器的传递函数:
(18)
2 模糊PID控制系统
2.1 传统PID控制结构
传统PID控制器由比例(Proportional, P)、积分(Integral, I)和微分(Derivative, D)3个环节组成。PID控制算法对受控对象的传递函数的模型没有特定的要求,只需要根据作业条件设定合适的比例、积分与微分的参数就能达到所需要的控制目标。
2.2 模糊PID控制结构
模糊PID控制主要由传统PID控制器和模糊化模块组成,其结构如图3所示。根据实际要求,以系统反馈的压力与给定值之间的偏差e和偏差变化率ec作为输入,利用量化因子Ke与Kec将其转换为模糊量,依据给定的模糊规则进行模糊推理,再通过模糊化的比例因子得到3个参数的变化量,与之前设定的PID参数进行合并,进而达到参数自整定的效果。
根据PID参数整定规则,得到自调整PID 3个参数的修正公式:
(19)
本文作者采用模糊PID控制设计了一种控制恒力输出器的力的方法。依据模糊控制原理,将e和ec的模糊论域均定为 [-3,3],输出的ΔKp的模糊论域为[-0.3,0.3],ΔKi的模糊论域为[-0.06,0.06],ΔKd的模糊论域为[-3,3]。根据模糊控制将上述5个模糊量的模糊子集均定为{NB, NM, NS, Z, PS, PM, PB},e、ec、ΔKp、ΔKi、ΔKd的隶属度函数全部选用三角隶属度函数,隶属度为[0, 1]。根据压力偏差e与ec对ΔKp、ΔKi、ΔKd依次构建模糊规则,分别如表1—表3所示。

表1 ΔKp控制规则

表2 ΔKi控制规则

表3 ΔKd控制规则
3 粒子群优化PID控制
3.1 粒子群算法
粒子群优化算法(Particle Swarm Optimization,PSO),是KENNEDY和EBERHART于1995年提出的,它源于对鸟群捕食行为的研究[11]。PSO因规则简单、收敛速度快等特点,被众多学者研究,并在PID控制参数优化整定中得到广泛应用[12-13]。
假设在一个D维的目标搜索空间中,有N个粒子组成一个群落,其中第i个粒子的位置记为Xi=(xi1,xi2,…,xiD),粒子速度记为vi=(vi1,vi2,…,viD),搜索到的最优位置记为pBest,i=(pi1,pi2,…,piD),整个粒子群搜索到的最优位置记为gBest=(pBest,1,…,pBest,i,…,pBest,D),在找到这两个最优值时,粒子根据式(20)和(21)来更新自己的速度和位置:
(20)
(21)
i=1,2,…,Nd=1,2,…,D
其中:ω称为惯性权重;c1和c2为学习因子;r1和r2为[0,1]内的随机数。
3.2 粒子群算法优化模糊PID
由于模糊PID中的量化因子和比例因子都为给定值,导致模糊PID系统自适应调参得到的不是最佳值,造成控制系统的局限性[14],所以引入粒子群优化算法对比例因子和量化因子进行优化。系统结构简图如图4所示。
3.3 改进粒子群算法优化模糊PID
传统的PSO算法比较容易陷入局部的最佳解,可以对惯性取值进行改进[15],引出线性递减权重:
(22)
式中:ωmax、ωmin分别为起始惯性权重与终止惯性权重;t为当前迭代次数;tmax为整个迭代过程中最大迭代次数。此方法能够满足惯性权重为动态变化过程,但是在算法优化的过程中惯性权重的变化率并未变化。为使惯性权重拥有动态的速度变化率,在线性惯性权重递减中加入混沌系数,使得惯性权重在线性递减时尽可能在曲线的下方发生振荡,惯性权重变化速率不再是固定的,进而增强全局搜寻能力。
ft=μft-1(1-ft-1)
(23)
混沌线性惯性权重递减系数为
ωnew=ωtft
(24)
式中:ft为第t次迭代的混沌值;μ为混沌系数。
将ωmax=0.9、ωmin=0.1、μ=4、起始混沌值f0=0.63代入式(22)、(23)和(24),并根据所得数据绘制出图5。可知:混沌递减系数在保证总体的惯性系数不断减小的同时能在较小范围内振荡,避免了算法陷入局部最优。
采用改进粒子群优化模糊PID控制参数时,每个参数之间相互影响,要求所有指标都达到最佳是不可能的,故需要一个确定误差是否最小的评价性能指标。引入性能指标函数ITAE作为恒力输出器控制系统性能评价指,其表达式为
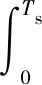
(25)
基于图4,设计改进粒子群算法优化PID控制流程,如图6所示。
4 仿真与实验分析
4.1 仿真分析
改进粒子群优化模糊PID参数设置:种群规模N=10,粒子维度D=5,学习因子c1=c2=1。5个粒子的速度的最大值均为1、最小值为-1;5个粒子的最小位置矩阵为[1.29,1.29,2.75,0.35,0.85]、最大位置矩阵为[1.68,1.68,3.25,0.66,1.03]。 PID 3个参数为Kp=4.978、Ki=0.001、Kd=1。
将上述参数代入模糊PID控制器,则系统中采用未优化的模糊PID控制和文中提出的基于改进粒子群算法优化模糊PID控制下的阶跃响应能力如图7所示。
由图7可知:经过改进粒子群算法优化的模糊PID控制系统比模糊PID控制系统更快达到目标值,收敛速度更快,超调量也明显降低,整体的超调量为8.91%,在1.3 s达到稳定。
4.2 实验分析
使用基于恒力输出器打磨机器人对打磨对象进行打磨时,首先考虑的因素是打磨头与打磨对象之间的接触力。恒力输出器的输出力是否稳定决定加工件表面粗糙度是否均匀。由于在系统进行打磨抛光的过程中,末端的恒力输出器与打磨头可能会随着零件的轮廓改变自身位姿。为确保在该点的法线方向输出抛磨力,根据图8所示的受力分析图构建受力方程(26)。其中,m1为打磨头的质量;Fs为接触力。
Fs=p0A0-f+m1g
(26)
式(26)为恒力输出器与打磨工具处于垂直方向的受力方程,若零件属于曲面类零件,则在任意一点进行打磨抛光时恒力输出器与打磨工具这个整体与垂直方向成θ角,则受力方程为式(27):
Fs=p0A0-f+m1gcosθ
(27)
忽略气缸与活塞摩擦力,可得简化后的恒力输出器的输出力公式:
F=Fs-m1gcosθ
(28)
4.2.1 恒定输出力实验
实验采用气袋作为被挤压对象是因为气袋中含有足量的气压,若输出力过大或大幅度变化对其进行挤压,则气袋容易爆裂。实验中保证恒力输出器垂直挤压气袋,如图9所示。分别采用模糊PID控制方法和改进粒子群算法优化PID控制方法,采集到2种控制方法的输出力变化数据,并绘制输出力变化图,分别如图10、图11所示。
整个实验过程中气袋未发生破裂。观察图10与图11能够得出整个实验过程中基于粒子群改进算法优化的模糊PID控制的抛磨力相对模糊PID控制的输出力变化幅度更小且更加稳定,力跟踪效果较好。
4.2.2 正弦输出力跟随实验
由式(28)可知,恒力输出器的输出力与三角函数相关。为监测在2种控制方法下输出力的跟随状态,设计正弦力跟随实验。将正弦力的振幅设置为10 N,偏距设置为20 N,频率为0.4 Hz,同样采取上述2种控制方法,并将采集到的正弦力变化数据绘出图,分别如图12、13所示。由图12可知:两者的力跟随性都较好,且误差相差不大,均在1 N以内,但是改进粒子群优化的模糊PID控制的响应速度更快。表明在误差允许范围内,改进粒子群算法优化的模糊PID控制的恒力输出器拥有更快的响应速度。
4.2.3 打磨抛光实验
以40 cm×23 cm铝薄板为实验对象,并采用改进粒子群算法优化模糊PID控制系统控制恒力输出器进行打磨实验,如图14所示。输出力设置为10 N,对铝板进行打磨,同时采集打磨过程中实际抛磨力的大小,并将数据绘制成折线图,如图15所示。可知:实际的抛磨力误差能够保持在±0.3 N内。
5 结论
针对模糊控制中的量化和比例因子均为固定值、造成控制系统局限性的缺点,提出一种基于改进粒子群算法优化的模糊控制,不断迭代寻优出最佳的量化和比例因子。结果表明:经过改进粒子群算法优化的模糊PID控制系统超调量更低、响应速度更快、收敛速度更快、恒力输出器输出力变化幅度更小且更加稳定,验证了改进粒子群算法优化模糊PID控制策略的有效性。

