基于惯性导航的电缆管道测绘装置及其测试误差分析

何嘉玮，宋 宁，侯东雨，金 毅，肖 亮，肖俊昱，蒋晓娟

(上海市电力公司电缆分公司，上海 200070)

随着城市规模的扩大，越来越多的电力电缆应用于城市电网中，确保电缆管道的安全已成为保障电缆安全运行的关键。在城市建设过程中，因电缆路径坐标不准确导致的电缆外破事故时有发生，已成为引发电缆故障的主要原因之一[1]。传统的地下电缆管道路径检测方法主要有音频感应法和电磁法[2]，这两种方法具有许多局限性，音频感应法的检测精度不高，只能通过耳机听到的最大声音来判断电缆的位置，电磁法检测性能不稳定，易受到电磁和铁磁干扰的影响。惯性导航技术近年来发展迅速，将惯性导航技术与管道定位技术相结合进行地下管道路径定位测量是一种可行的实践操作。该种方法不仅能够克服传统定位检测方法的缺点，而且惯性导航定位技术的诸多优点都与管道定位检测技术相契合，例如具有高度自主性，不会受到外部电磁信号的干扰，不依靠外部信息进行定位、也不向外部辐射能量，并且还具有在复杂条件下全天候工作的能力[3-5]。

通过对惯性导航原理的分析，本文设计了一套地下电缆管道路径的三维测绘装置。该装置利用惯性导航模块对载体运行过程中的三维加速度和角速度进行测量，结合初始位置，利用惯性导航模型沿线各点的坐标进行解算，然后利用里程校准的卡尔曼(Kalman)滤波修正算法实现对地下管道路径三维坐标的精确测试。

在此基础上，利用该装置在不同条件下对相同管道进行测试，并对影响装置测试精度的因素进行分析。

1 惯性导航原理

惯性导航系统(INS)是一种不依赖于外部信息、也不向外部辐射能量的自主式导航系统。其基本工作原理是以牛顿力学定律为基础[6]，通过对载体在惯性参考系下加速度和角速度的测量，将它对时间进行一次和二次积分，通过姿态矩阵将其变换到导航坐标系中，就能够得到在导航坐标系中的速度、偏航角和位置等信息。姿态矩阵的具体表达式如下：

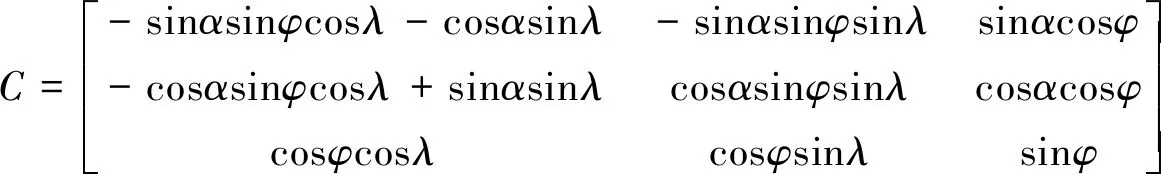
(1)

式中φ——俯仰角；α——航向角；λ——横滚角。

惯性导航计算原理如图1所示。在进行惯性导航测绘的过程中，利用惯性导航模块对运载体行径过程中的三维加速度和角速度进行测量，通过对时间的积分测得运载体的速度和运载体的偏航角等连续的信息，结合运载体的初始位置坐标，以此推算出运载体行径过程中各点的坐标[7]：

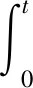
(2)

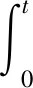
(3)

式中vt，Xt——当前时刻运载体的速度和位移信息；v0，X0——初始时刻运载体的速度和位移信息；At——惯性测量单元获取的加速度信息。

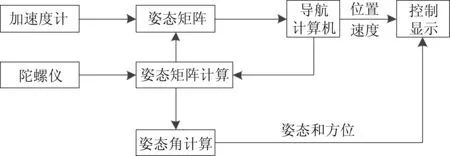
图1 惯性导航计算原理图

2 卡尔曼滤波算法

由惯性导航定位原理可知，在定位过程中直接采用惯性导航模块(IMU)所测量的数据进行定位解算时，系统的测量误差是累加的过程，其测量误差随着定位距离的增加而增加。为了实现对定位坐标的修正，提出了基于里程校准的卡尔曼滤波算法，利用磁开关对运载体行径的里程进行测量，利用每步里程对同一时刻由惯性导航测量值得到的里程进行修正，减小测量误差累加对测试精度的影响，即减小测量偏移量，达到提高测试精度的目的。

利用磁开关脉冲计数的方式实现对路程和速度的测量，如图2所示。整个系统由磁开关和带磁粒的轮毂组成，在工作过程中，轮毂在系统行径中旋转，当磁粒接近磁开关时，给其一个磁信号，触发磁开关，形成一个脉冲信号。通过对脉冲信号的计数和间隔时间的测量，实现对系统行径路径长度和速度的测量，其计算公式如下：

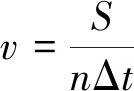
(4)

式中S——路程；l——两个磁粒之间的弧长；n——计数值；v——平均速度；Δt为脉冲的时间间隔。

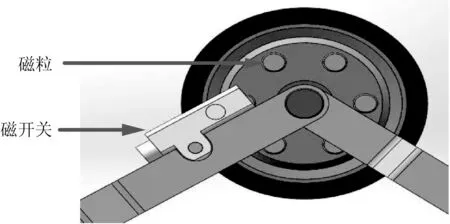
图2 里程计的结构示意图

将n系下INS计算的速度、姿态以及位置误差作为Kalman滤波估计的状态量X：

(5)

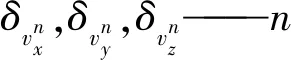
在误差修正的过程中，将里程计测得的速度与根据惯性导航原理计算的速度之差作为观测量Z：

(6)

式中vn——根据惯性导航原理计算的速度；vln——里程计测得的速度。

根据卡尔曼滤波原理，利用式(4)和式(5)定义的状态量和观测量构建微分方程：

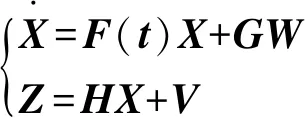
(7)

式中F(t)——系数矩阵；G——白噪声系数矩阵；H=[03×3I3×303×3]——量测矩阵；W——动态噪声矢量；V——测量噪声矢量，且W与V互不相关。

根据基于里程校准的卡尔曼滤波算法，设计了管道路径定位计算流程，如图3所示。整个计算过程分为数据预处理、INS解算和卡尔曼滤波算法3步骤。

(1)数据预处理：首先利用形态学滤波对IMU采集到的加速度和角速度波形进行修正，消除振动过程中形成的毛刺信号。

(2)SINS解算：利用惯性导航解算算法对形态学滤波出来后的数据进行解算，得到载体运动的轨迹信息。

(3)自适应Kalman滤波估计：以里程计测量速度和根据惯性导航原理计算的速度之差作为观测量，利用Kalman滤波方程得到系统状态的最优估计值，利用估计值对根据惯性导航原理结算的数据进行修正，最终得到精确的定位坐标。

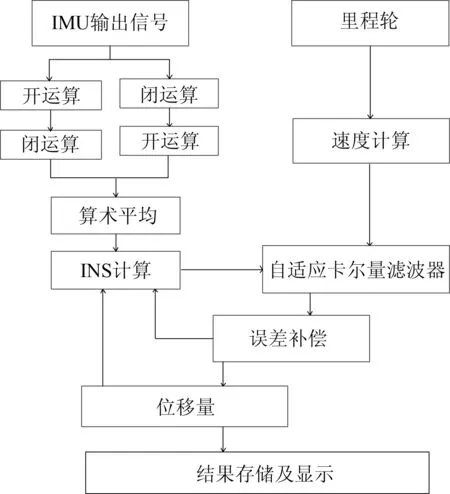
图3 管道路径定位系统算法框图

3 影响测试精度因素分析

3.1 定位装置的制作

由于管道处于地下，GPS(或北斗)信号无法在地下接收，而惯性导航技术通过对行程过程中加速度和角速度的测量，基于始末端的初始位置信息，可实现对地下管道路径的定位。本文根据惯性导航原理设计了一套可用于地下管道定位测量的装置，如图4所示。定位装置主要由电子舱、支撑支架、轮组3部分组成，靠外力牵引在管道内行走。电子舱内安装有主控电板、惯性测量单元、红外摄像头及固定支架，支架带有减振装置。电子舱与前后支撑支架采用螺纹连接，且使用安全插销防脱锁紧。支撑支架由滑动轴、骨架、弹簧、连接附件等组成。 轮组安装在支架上，支撑支架可以根据实际管径大小，随意调节轮组支撑状态，靠弹簧的张力将电子舱支撑保持在管线的中心线位置和沿中心线行走。

图4 管道定位装置图

3.2 试验平台的搭建

为了验证管道定位装置的可行性，分析不同测试条件对系统测量精度的影响，对整个测试平台进行了搭建，整个装置的试验示意如图5所示。为了消除初始振动对测量的影响，在牵引前将系统静止5 min，最后人工(或机械)将地下电缆管道路径的三维测绘装置牵引至管道的另一端，然后再次静止5 min，对设备进行回拉，然后读取数据，利用解算程序对测量数据进行解算，实现对管道路径的测绘。

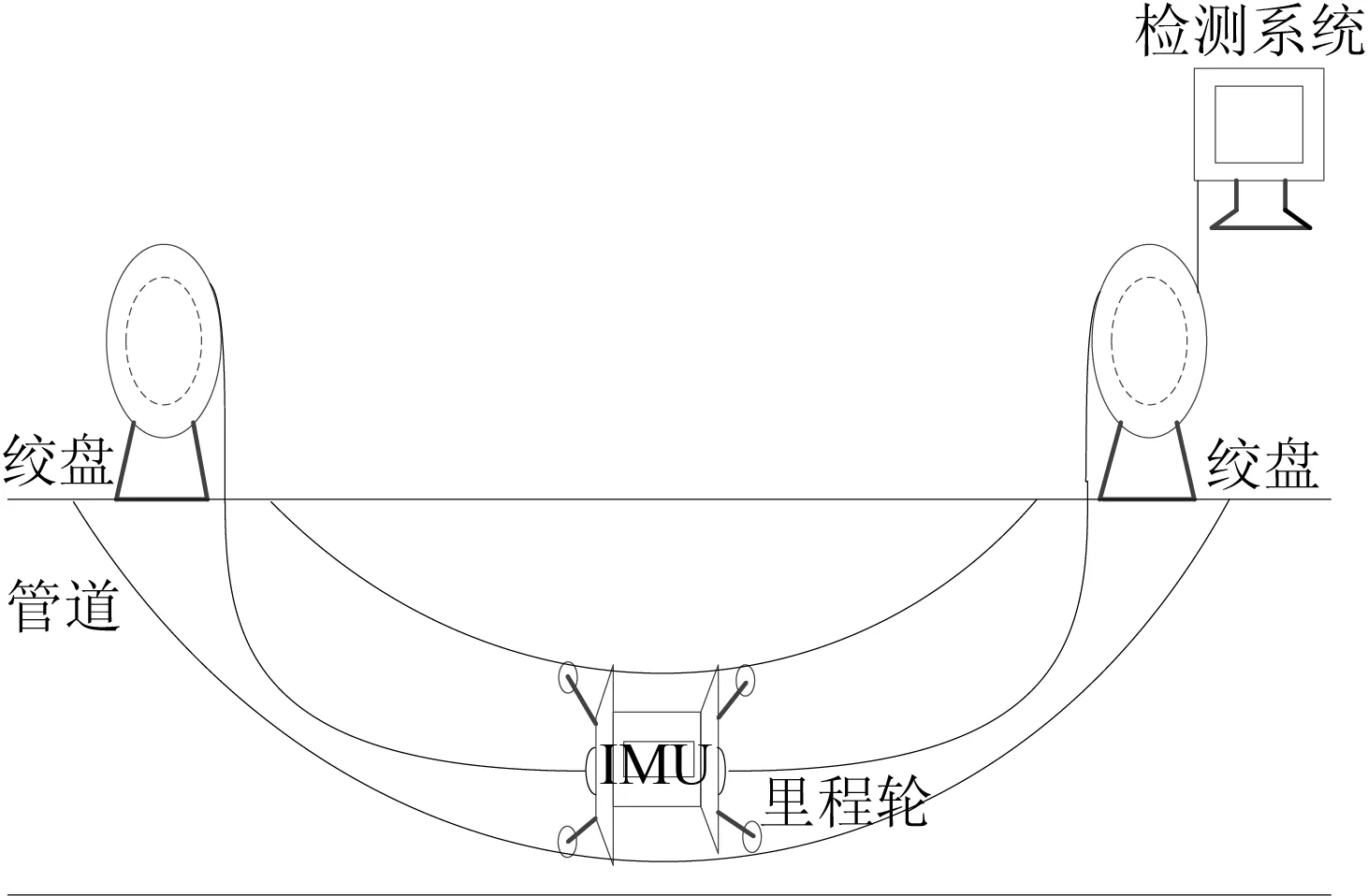
图5 路径定位装置试验示意图

3.3 试验数据分析

在试验过程中，对不同振动程度、采样频率和行进速度匹配程度下的数据进行了测试，结果如图6和表1所示。

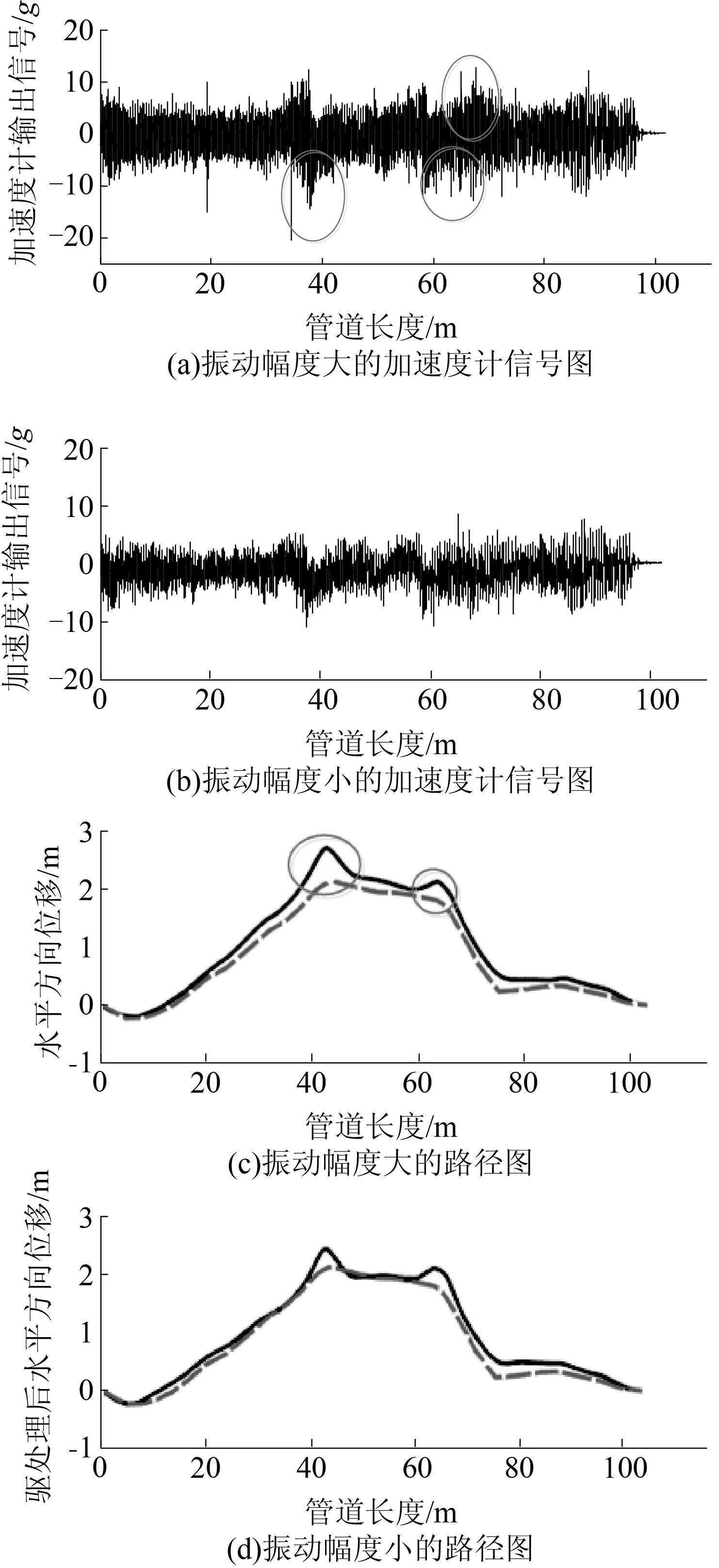
图6 不同振动强度的测试结果

表1 不同采样频率和行进时间的匹配程度测试结果 m

由图6可知，虚线为实时动态(RTK)校准波形，实线为测量曲线。通过对图7中振动强烈状态不同的测试数据可以看出，系统在管道行径过程中振动程度较大时，其加速度的输出信号剧烈，由原来的最大幅值10g上升到20g，导致路径位置的偏移也变大。通过对惯性导航定位原理的分析发现，造成振动状态下测量误差偏大的主要原因是：系统在测量过程中，当振动幅度较大时，根据惯性导航原理测量的加速度数据偏大，这造成了定位测量数据误差变大。

由表1的测试数据可知，基于惯性导航的电缆管道三维坐标测绘系统的测量精度随着采样周期与行径时间误差的增加而降低。这是由于随着误差时间的增加，影响路径的位移误差变大，通过误差积加，导致测量误差增大。

4 结语

通过对基于惯性导航电缆管道三维坐标测绘技术的研究及影响测量精度误差的分析可知，利用惯性导航原理，结合起始点和终点的坐标，可实现对地下电缆管道路径三维坐标的精确测绘。同时，在测绘过程中，装置的测量精度受振动幅值的增大以及采样周期与里程计数周期之间偏差的影响，其测量精度随着振动幅值和采样周期与里程计数周期之间偏差的增加而降低。