基于热路模型的电力电缆温升计算方法综述

赵莹莹，鲍长庚，姚维强，倪 浩，沈东明，钱之银

(1.华东电力试验研究院有限公司，上海 200437； 2. 国网上海市电力公司，上海 200122；3. 上海海能信息科技股份有限公司，上海 201315)

电力电缆大多工作于地下，环境密闭且散热条件一般，线芯导体损耗、绝缘介质损耗等产生的热量，造成了电缆本体温度升高，这在很大程度上决定了电缆的绝缘老化速度、绝缘寿命等。准确计算电缆温升，无论是对设备检修，还是运行调度都具有重要意义。电力电缆温升受电缆本体结构、敷设方式、运行负荷、外部环境等多个因素影响。电缆本体结构和运行负荷决定了热源和热量大小，电缆敷设方式和外部环境决定了传热(散热)方式和传热过程。电缆温升计算即是在给定电流负载的条件下，求解导体温度，对给定的导体材料和负载，需要计算在电缆内产生的热量及导体的散热率。

1 传热学基础

传热学是研究由温差引起的热能传递规律的科学。传热可以发生在任何有温差的物体之间，热能的传递有热传导、热对流和热辐射3种基本方式[1]。

1.1 热传导

热传导是指物体各部分间不发生相对位移时，依靠分子、原子及自由电子等微观粒子的热运动而产生的热能传递过程。导热的基本定律是傅里叶定律，其一维稳态导热的数学表达式如下：

(1)

式中λ——导热系数；负号——热量传递方向与温度升高的方向相反；Ø——单位时间内通过某一给定面积A的热流量；q——热流密度；dt/dx——沿x方向的温度变化率。

1.2 热对流

热对流是指由于流体的宏观运动而引起流体各部分之间发生相对位移，冷、热流体相互掺混所导致的热量传递过程。热对流仅能发生在流体中，由于流体中分子同时在进行不规则的热运动，因此热对流的发生伴随着热传导现象。热对流包括自然对流与强制对流两大类。对流的基本计算公式为牛顿冷却公式，流体被加热时：

q=h(tw-tf)

(2)

流体被冷却时：

q=h(Tf-Tw)

(3)

式中q——热流密度，W·m-2；tw——壁面温度， ℃；tf——流体温度， ℃；h——表面传热系数，W·(m2·K)-1，h的大小不仅取决于流体的物性以及换热表面的形状、大小与布置等，还与流体速率有密切的关系。

1.3 热辐射

物体通过电磁波来传递能量的方式称为辐射，其中因热的原因而发出辐射能的现象称为热辐射。热辐射不仅产生能量的转移，而且还伴随着能量形式的转换。热辐射热量的计算方法为斯忒藩-玻耳兹曼定律：

q=σT4

(4)

式中q——热流密度，W·m-2；T——辐射物体的热力学温度，K；σ——斯忒藩-玻尔兹曼常数，为5.67×10-8W·(m2·K4)-1。

2 电力电缆的传热学问题分析

2.1 运行中的电缆热源

损耗是引起电缆发热的主要原因，当电流通过电缆导体时，导体电阻产生焦耳热损耗，引起导体温升，产生的热量部分储存在导线和绝缘材料内，其余热量经绝缘材料传导至电缆表面和周围介质，最后土壤与空气边界产生对流与辐射换热。经过一个较长的暂态过程，电缆的温度逐渐达到稳定，产热与散热达到平衡。电力电缆的热源主要包括线芯导体的交流电阻损耗、绝缘介质损耗、金属护层损耗和铠装层损耗等[2]。温度的变化会导致材料的电阻发生变化，从而使损耗发生改变。

“我是秀姐哩。”秀姐的手很温暖很柔和，如一枚圆润的玉器，秀姐紧紧地握住我的手，直到我又昏昏沉沉地睡去。

导体交流电阻损耗包括直流损耗和由交变电流引起的涡流损耗，涡流损耗可以用邻近效应和趋肤效应表示。绝缘介质损耗由交变电压作用在绝缘层上的交变充电电流引起。金属护层损耗包括环流损耗与涡流损耗。若电缆护层两端短接，涡流损耗可不计；当电缆护层单端接地或两端交叉互联接地时，环流损耗可不计[2-4]。

IEC 60287给出了两种情况下的金属护层损耗因素计算公式。对于铠装层损耗，非磁性材料铠装损耗可以用金属护层损耗计算公式计算，磁性材料铠装损耗则需要单独计算。

2.2 不同敷设条件下的电缆传热方式

地下电力电缆的敷设方式主要有直埋敷设、排管敷设、沟槽敷设和隧道敷设等。对于土壤直埋电缆，电缆本体及土壤中的热扩散主要以热传导的形式进行。排管敷设电缆在电缆和排管壁之间存在一层空气层，这部分介质的传热方式主要是热对流和热辐射，因此排管内电缆的散热方式包括传导、对流与辐射3种形式[3]。传导与辐射表示相对固定，对流的程度受到空气性能、温度、几何尺寸等因素的影响，并且随电流、环温等工况差异而有所不同。排管敷设电缆涉及流场和固体介质的热传导场的耦合计算，而流场的计算需要不断地迭代，很难准确获得其热扩散的特性，这给地埋排管电缆的线芯温升计算带来了巨大的困难。电缆进出变电站处多采用沟槽敷设方式，沟槽敷设电缆靠近地面，其散热易受到日照、风速等环境因素影响。与排管内电缆一样，沟槽内电缆的散热方式也包括了传导、对流与辐射3种形式，但沟槽内部对流传热和辐射传热存在非线性。隧道敷设是高压电缆敷设的主要方式之一，其散热只能通过空气对流与辐射方式进行，传热效率略低于其他几种方式。

3 基于热路模型的电缆稳态温升计算

热路模型的提出基于热路和电路的相似性，将电缆与周围环境的温度场类比于电场中的电路，在传热学中产生的是热量的转移，转移受温度差驱动，转移过程中会受到热阻的阻碍[5]。热路模型一般用来计算稳态温度场下的载流量，最早是由Kennely提出，之后Neher和McGrath进行了完善。国际电工委员会(IEC)在此基础上制定了电缆额定载流量计算标准IEC 60287和暂态载流量计算标准IEC 60853。

IEC 60287中典型的电缆等效热路模型如图1所示。

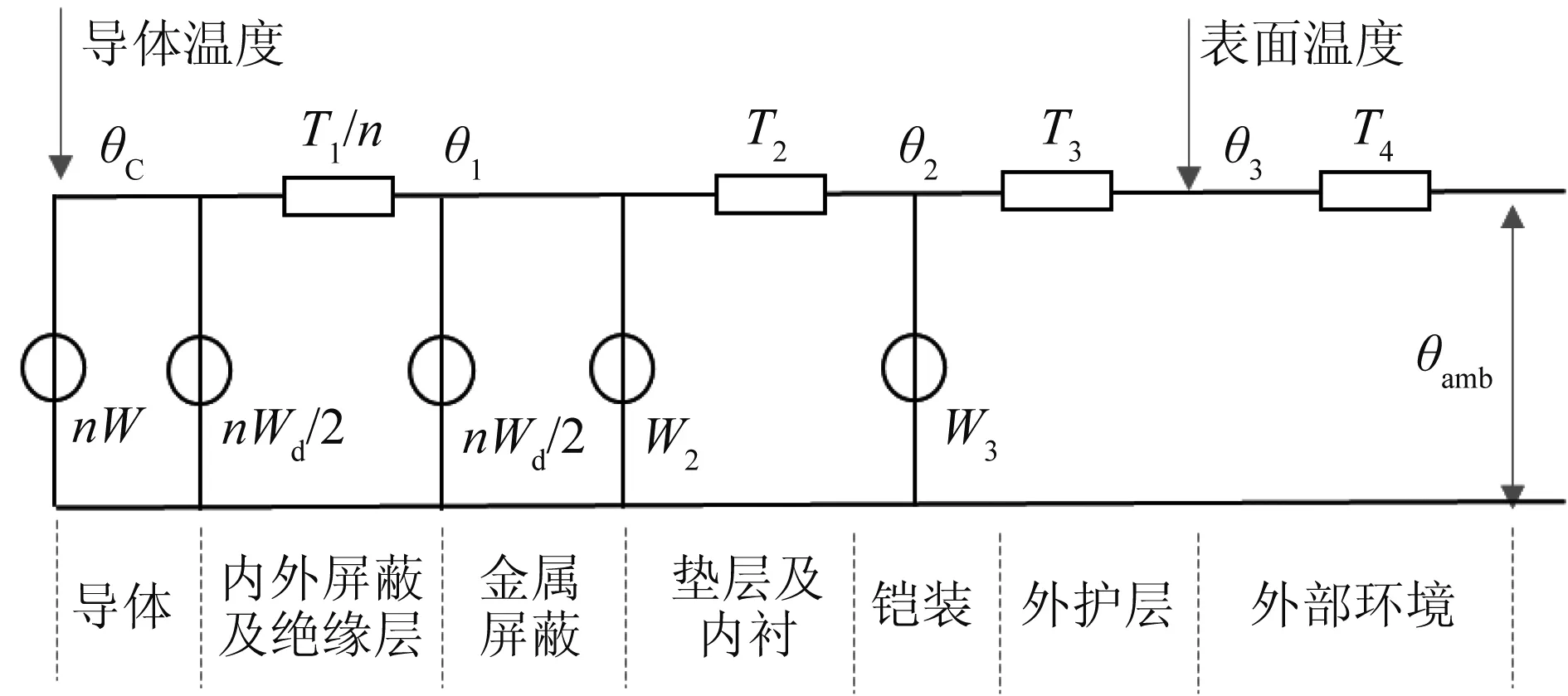
图1 电缆稳态热路模型

根据节点法，可以得到电缆稳态时导体温升公式[2]：

θC-θamb=(W+0.5Wd)T1+
(nW+nWd+W2)T2+
(nW+nWd+W2+W3)(T3+T4)

(5)

国内外学者在基于热路模型计算导体温升方面开展了大量研究，主要包括以下方向：围绕电缆本体进行热路模型改进以及热阻等参数计算；对地埋电缆群的稳态温升建模研究，包括不同敷设方式下的电缆群和电缆间排布位置的影响研究；对电缆敷设的外部环境如土壤热阻等开展研究。

电缆本体模型方面，文献[6]采用调和平均法对电缆的各个薄层进行处理，并将其等效为同一个导热系数和厚度的护套层，电缆模型仅有两层，同时不影响计算结果的精度；文献[7]讨论了三芯电缆的“品”字形结构导致各径向传热特性不同，构建了三芯电缆的热路模型；文献[8-11]基于排管、隧道等不同敷设条件下电缆传热方式不同，分别构建了导热散热热阻、对流散热热阻和辐射散热热阻，并提出了相对应的散热方式和热阻的量化规律，构建了不同敷设方式下的基本热路模型。在热阻和损耗参数计算方面，虽然IEC 60287给出了热路模型及参数计算公式，但是计算结果相对保守。国内外大量学者采用有限元仿真和试验方法，进行了参数求解和优化，以确定给定电缆的导热系数和各层材料的热阻系数。

在电缆群的稳态温升计算方面，文献[10-13]针对电缆群温升的工程化快速计算需求，提出了一种基于转移矩阵来实时估算电缆缆芯温升的方法，可以用于直埋和排管电缆群的稳态温升计算。该模型基于热场叠加原理，将多回电缆的共同作用离散为多根电缆单独作用的组合。通过有限元仿真计算结果，获得电缆本体缆芯温升与发热样本数据组，以及相邻电缆间的发热与温升样本数据组，再利用数据拟合，获得缆芯温升与缆芯损耗、介质损耗、金属套损耗，以及相邻电缆损耗之间的关系，获得自热导系数和互热导系数，从而求解电缆群缆芯温升的转移矩阵。该矩阵系数与负载、温度等因素无关，仅与周围介质的热特性参数相关。并且通过对12根两层三芯电缆群的有限元计算结果与转移矩阵计算结果的对比，验证了该方法具有较高的准确性，并且计算速度较快，便于现场工程人员使用。该方法建立在假设正常运行温度下，转移矩阵的参数不随温度的变化而发生变化。文献[14-15]针对隧道敷设方式下的500 kV超高压大截面电缆，分析了“品”字接触排布和水平排布不同安装方式下，表面间距和分组位置对电缆间互热和相互间散热效果。同时提出了接触和分离两种情况下水平排列电缆总散热系数的计算公式，用于快速求解导体温度，并通过有限元数值模拟，验证了模型的准确性，获得了总散热系数计算公式的适用范围。

在外部环境方面，IEC 60287中假设电缆周围的介质为单一均匀的介质，这对于长电缆线路，在实际环境下不易实现，环境参数难以单一确定。针对土壤介质，文献[16]对外部热阻模型进行了改进，依据实际敷设环境，将土壤细分为原始土壤、回填、上层回填、表层土壤等，利用数值仿真方法得到大量的不同外部环境下的电缆载流量，然后以仿真得到的载流量数据，利用粒子群等优化算法对载流量公式中的参数进行辨识，得到通用的载流量、温升计算公式。文献[17]对电缆敷设周围有水管等其他因素进行了细化研究。

4 基于热路模型的电缆暂态温升计算

运行负载的阶跃性变化会打破电缆发热散热平衡，电缆导体温度随之发生变化。由于电缆各层及外部电容的存在，导体温度随时间缓慢变化，最终达到稳定状态。暂态过程即是求解负载改变时电缆温度变化过程。IEC 60853给出了电缆暂态条件下的载流量计算公式，基于Van Wormer提出的一种简化的分配导体和护层间绝缘热容的方法。IEC 60853将电缆分为35 kV及以下和35 kV以上两类。对于35 kV及以下电缆，标准给出了在加载周期性载荷和短时负荷时的载流量计算公式，这类电缆可忽略热容影响。对于35 kV以上电缆，在周期性负荷下，电缆热容不可忽略，电缆线芯温度的变化为稳态温升和暂态温升两部分的总和，并将暂态模型分为短时暂态和长时暂态两种模型，并给出了相应的热容、热阻和温升计算公式。IEC 60853对电缆的内部和外部温升分别进行了单独的计算。内部和外部电路之间的耦合是通过假设流入土壤的热量与导体和电缆外表面之间的瞬态达到因子成正比来实现，其有效性依赖于热路模型给出的响应计算的一致性[18]。典型的电缆暂态热路模型如图2所示。

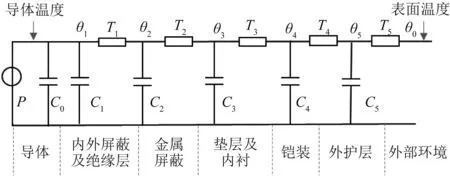
图2 电缆暂态热路模型

暂态模型方面，主要围绕电缆本体模型和电缆群暂态温升研究。

传统热路模型通过电缆表皮温度计算电缆导体温度时，电缆绝缘层集中处理，有较大的计算误差。针对此问题，文献[19-20]提出了一种优化绝缘层暂态热路模型方法。传统热路模型将电缆包覆层中的绕包带、气隙层、皱纹铝护套划分为独立的串联结构，然后分层计算出各自的热容、热阻参数，指出皱纹铝护套与绕包带间的空气介质存在强制对流传热热阻，并且皱纹铝护套凹进部分与绕包带接触存在接触热阻。由于电缆包覆层内部各层结构交错复杂、传热类型多样，不能将包覆层中的绕包带、气隙、皱纹铝护套视为独立结构串联建模。文献[21]提出了一种将绕包带、气隙层、皱纹铝护套合并为一层(包覆层)，构建高压单芯电缆暂态的热路模型。同时进行了暂态温升试验，求解热阻、热容参数，验证了将包覆层作为一层暂态热路模型的计算精度。文献[22]提出了一种利用平衡热阻和平衡热感模拟热扩散过程中热阻和热容的时变特性，从而建立不依赖外表测温的集中参数温升计算模型，提高土壤直埋单芯电缆暂态温升计算效率，并分别采用集中参数模型、有限元法与通用软件对同一工况进行计算对比，证明了该方法的有效性。该方法将电缆自身发热和环境温度影响分别建立模型，以适应外部环境温度的变化。

针对电缆群温升的暂态模型，文献[23]提出了一种基于时域响应和热传导场可叠加原理的方法，用于对土壤直埋电缆群暂态温升的快速计算。将电缆群的共同作用离散为多根电缆单独作用的组合，单根电缆自身发热利用自响应模型描述，电缆间的相互影响利用互响应模型描述，并通过节点温升耦合与损耗实时修正的方式来获得电缆线芯综合温升，从而实现暂态温升的快速计算。通过计算典型工况的暂态温升过程，并与计算软件结果进行了比较，验证了该方法的有效性。

5 结语

电缆绝缘的最高温度，限制了电缆的最大输送容量，也决定了电缆的剩余寿命。因此构建电缆稳态和暂态温升的热路模型，准确计算电缆导体的温度，无论对电缆的安全运行，还是负荷调度都十分重要。尤其是通过电缆暂态温升模型，可以实现运行电缆在负载变化情况下导体温度的实时计算，服务运行电缆的在线监测和动态增容，确保线路运行安全的同时，提升现有线路的输送容量。