基于PSCAD/EMTDC的高压直流输电准稳态模型的仿真验证

孙慧平，王西田，戴俊杰

(1.国网上海市电力公司，上海 200122； 2.上海交通大学电气工程系电力传输与功率变换控制教育部重点实验室，上海 200240； 3.国网上海市电力公司长兴供电公司，上海 201913)

目前我国已有多个高压直流输电(HVDC)工程和(直流)背靠背联网工程陆续投入运行，交直流混合大电网正逐步形成。研究交直流系统之间的相互影响，特别是系统发生干扰或故障后交直流系统的动态行为，是交直流电力系统分析的重要内容[1]。为了进行这些动态分析，首先要研究直流环节的数学模型，而根据所研究问题的性质采用不同精度的直流模型对分析至关重要[2]。一般认为HVDC的电磁暂态模型能够准确详细地描述HVDC系统包括换相失败在内的动态行为，但由于该模型的计算步长较短，因此电力系统的稳定分析中常采用HVDC的准稳态模型。

文献[3]通过对比HVDC准稳态模型的理论计算值和使用PSCAD/EMTDC对简化的直流输电系统进行仿真，证明了准稳态模型的有效性。HVDC的准稳态模型和电磁暂态模型的仿真对比尚未在统一的详细的仿真平台下进行，没有考虑对于不同的频率响应下准稳态模型的准确性，而这对研究交直流系统的低频振荡和次同步振荡具有很重要的意义。本文在PSCAD/EMTDC中利用其自定义模块功能建立换流器准稳态模型，在统一的仿真平台下与HVDC的电磁暂态模型进行仿真对比，并通过对比HVDC系统定电流控制设定值发生不同频率的扰动情况，定量地验证HVDC准稳态模型的有效性。

1 HVDC准稳态模型构建

HVDC系统示意图如图1所示。采用准稳态模型时可以认为带负荷调节分头变压器的分头动作太慢，可令其固定不变；假定交流母线电压三相平衡。直流准稳态模型需要考虑换流器模型、直流控制系统模型、直流线路模型和交直流系统的接口。根据其对直流线路和控制系统动态仿真的精确程度可划分为简单模型、响应模型和详细模型[4]。详细的准稳态模型系统接口如图2所示。图2中，下标r和i分别表示整流侧和逆变侧参数；Vd为换流器直流电压；V为换流母线交流电压；I和Id分别为交流侧和直流侧电流；α和β为触发角。

图1 HVDC系统示意图

图2 HVDC准稳态模型的接口连接图

2 准稳态模型在PSCAD/EMTDC中的建模实现

HVDC的准稳态模型在PSCAD/EMTDC中实现的重要环节就是对于接口的处理。在操作过程中往往把接口等效成电源来处理。对于电源的等效，PSCAD/EMTDC中有两种等效：一是基于节点的电流源等效，即诺顿等效；另一是基于支路的电压源等效，即戴维南等效。现以HVDC整流侧为例来说明在HVDC准稳态建模中接口的处理，根据准稳态模型的接口表达式[1]，如图3所示；将HVDC的直流侧等效成戴维南等效电源，向直流线路侧提供电压，其中Rdr为阻值很小的电阻；把HVDC的交流侧等效成诺顿等效电源，向交流母线侧提供电流，其中Rr为阻值很大的电阻，实现与外部电路的接口。HVDC系统的逆变侧的接口处理与整流侧的类似，不再赘述。

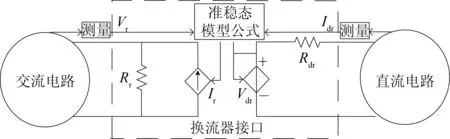
图3 整流器的接口等效原理图

在PSCAD/EMTDC中的换流器的准稳态自定义模型如图4所示。图4中，A、B、C为交流电气节点，表示换流器与交流母线的连接；PH、PD为直流电气节点，表示换流器与直流线路的连接；AO为控制信号节点，表示控制信号的输入。这与PSCAD/EMTDC元件库中的HVDC的电磁暂态模型的接口保持一致。在系统动态子程序(DSDYN)中嵌入相关程序，并通过调用外部FORTRAN语言的子程序来实现对准稳态方程的描述。在这种嵌入方法中，当前仿真步首先获取上一个仿真步网络求解得到的交流电压和直流电流的历史数据，据此求解准稳态方程，根据求解结果更新网络的交流电流和直流电压，然后再进行当前仿真步的系统网络的求解。求解过程如图5所示。

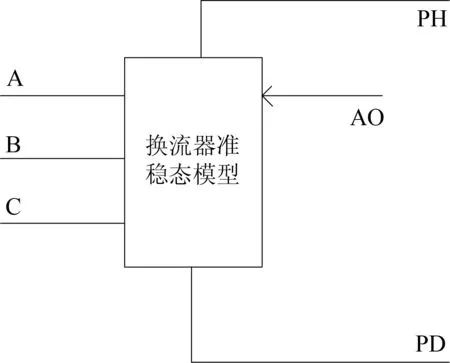
图4 PSCAD/EMTDC中的准稳态模型图

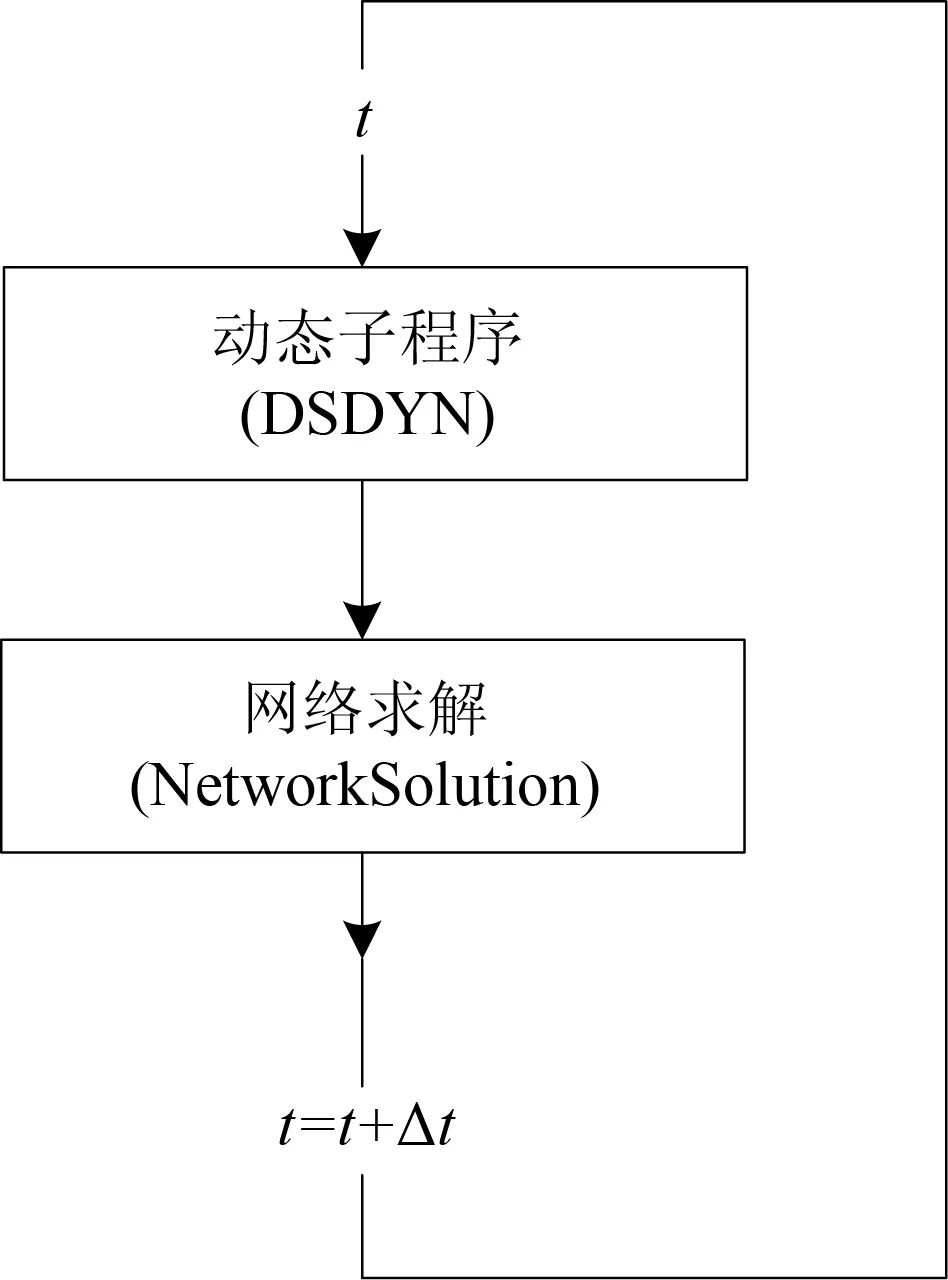
图5 PSCAD/EMTDC的主程序结构

3 仿真验证

3.1 仿真条件

该仿真基于HVDC的基准系统。一套系统为PSCAD/EMTDC中的HVDC基准系统，另一套系统为直流换流器采用准稳态的自定义模型，其他元件均采用PSCAD/EMTDC元件库中的元件，与第一套系统一致。HVDC系统为12脉冲系统，整流侧为定电流控制，逆变侧采用定熄弧角控制，自定义模型中的准稳态模型采用其详细模型。仿真主要对比系统发生小扰动时的情况，所设扰动为整流侧的定电流控制的设定值(标幺值)分别发生0，0.4，2，10，30 Hz振荡,振幅为0.05。仿真选取系统平稳运行后的结果。

3.2 仿真结果

图6～10为仿真得到的结果。图中实线为采用PSCAD/EMTDC元件库中的直流电磁暂态模型的仿真结果，虚线为采用直流准稳态模型的仿真结果。图中自上到下依次显示整流侧交流A相的电流和电压，整流侧直流电流和电压和直流系统传输的功率。由图6～10可知：发生0 Hz扰动时采用准稳态模型与采用电磁暂态模型的仿真结果相当接近；当发生频率为0.4，2 Hz的扰动时，仿真的结果也比较接近；当发生频率为10 Hz的扰动时，两者的功率曲线开始有些偏差，但总体仍比较接近；当发生频率为30 Hz的扰动时，两者的功率曲线出现比较明显的偏差。这也就说明在HVDC的准稳态模型低频段时其具有较好的精确度，随着扰动频率的升高，模型的精确度开始变差。在低频振荡(0～2 Hz)分析中可以使用准稳态模型；在次同步振荡(2～50 Hz)分析中，若所关心的次同步振荡的频率较低时，仍然可以使用该模型，若所关心的次同步振荡的频率较高时，则要慎重考虑使用该模型。

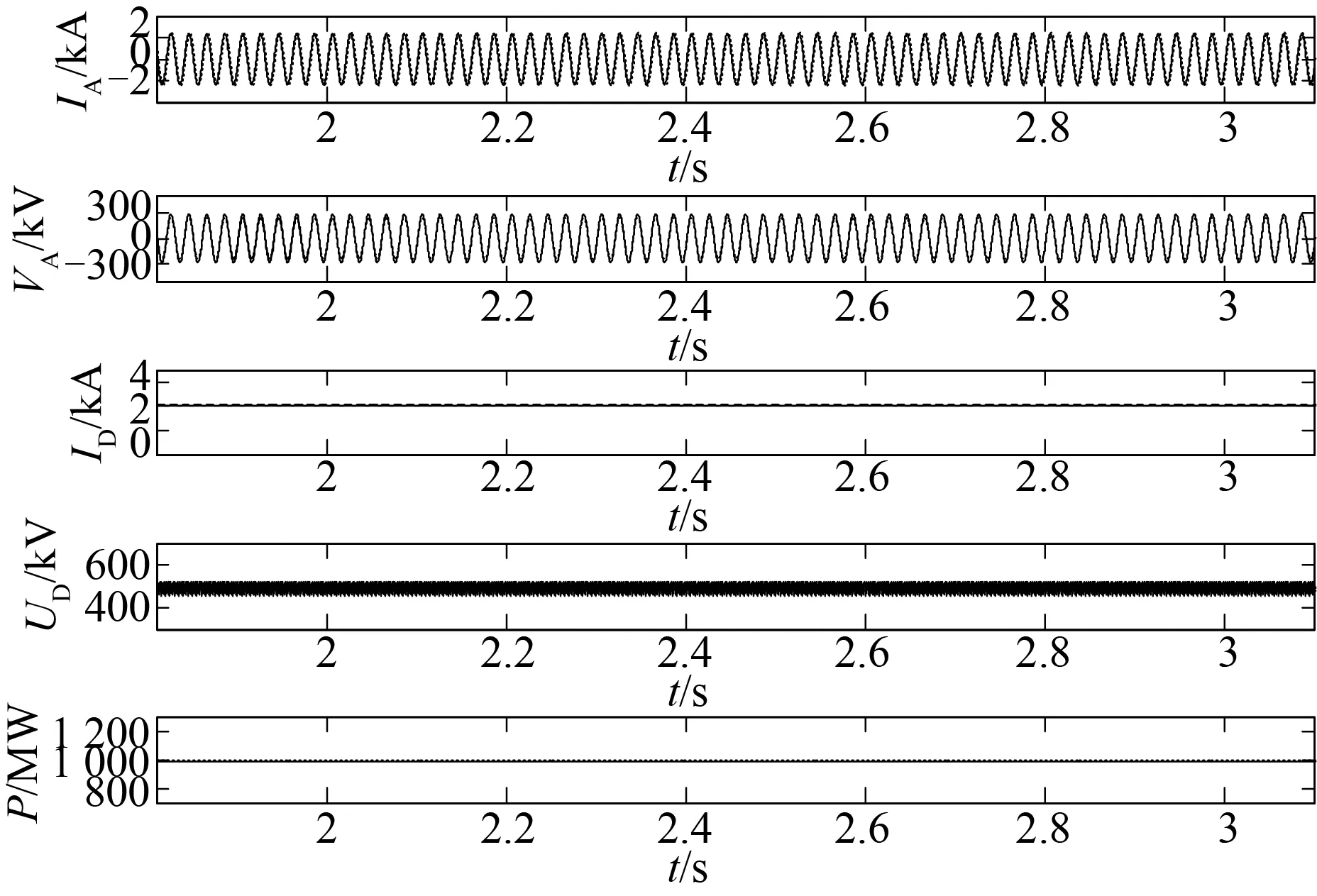
图6 定电流控制发生频率为0 Hz扰动的仿真结果比较

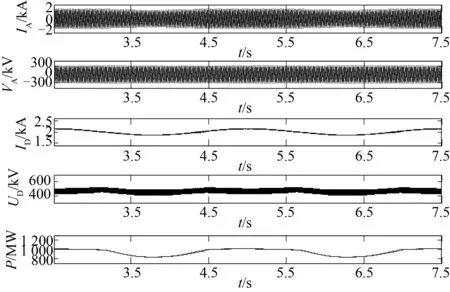
图7 定电流控制发生频率为0.4 Hz扰动的仿真结果比较

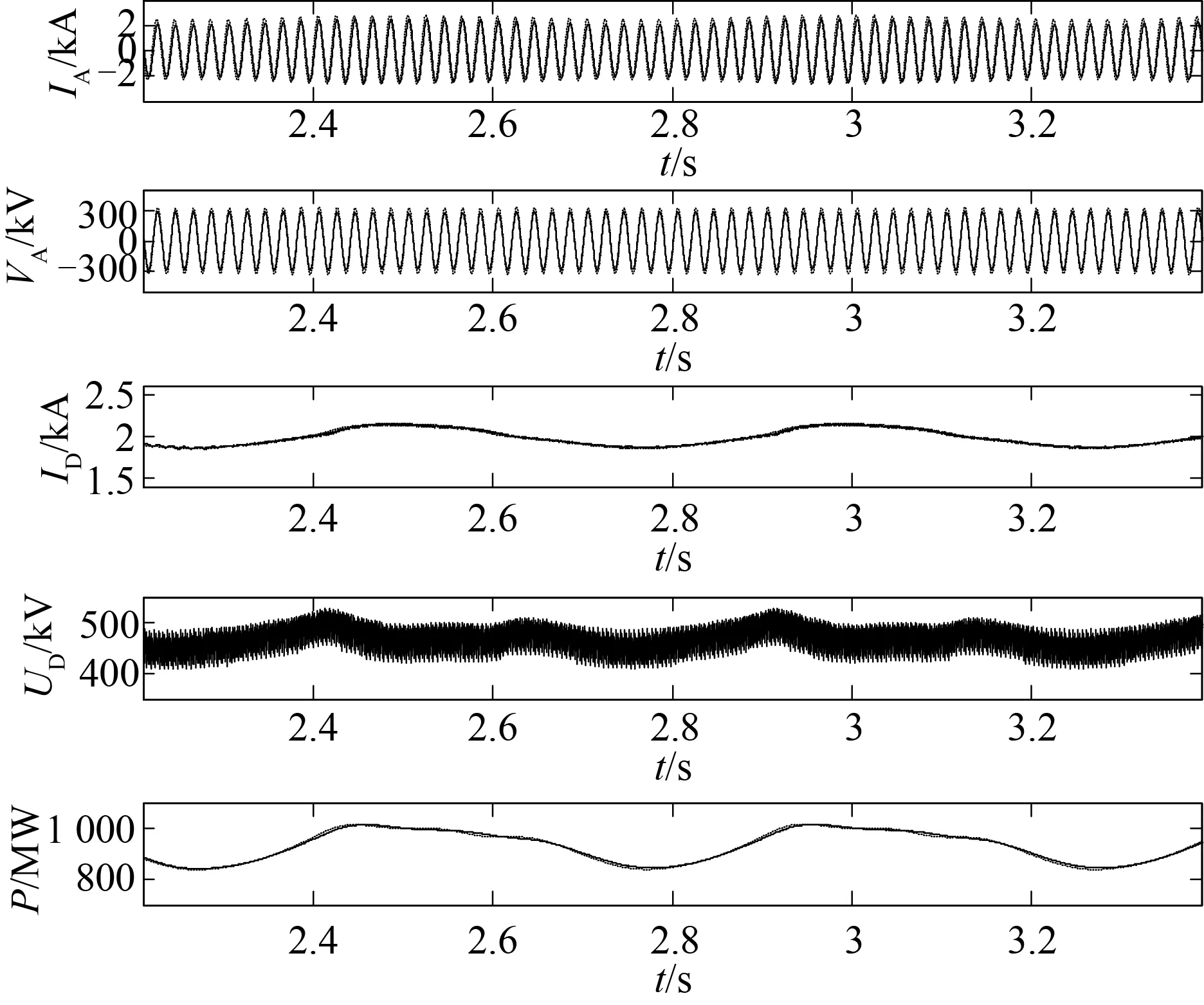
图8 定电流控制发生频率为2 Hz扰动的仿真结果比较

图9 定电流控制发生频率为10 Hz扰动的仿真结果比较

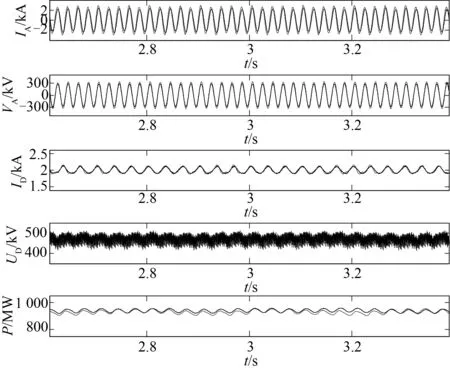
图10 定电流控制发生频率为30 Hz扰动的仿真结果比较

4 结语

本文采用详细的准稳态模型对12脉冲HVDC系统进行建模，在PSCAD/EMTDC的自定义模块中建立HVDC的准稳态模型，与PSCAD/EMTDC元件库中的直流电磁暂态模型进行了仿真比较，对比不同频率的扰动下直流的系统相关参数。结果显示：在扰动频率较低时HVDC准稳态模型的准确度更高，可以用于电力系统低频振荡的分析；若次同步振荡中的振荡频率较低时也可以使用该模型进行分析。

在统一的电磁暂态仿真环境下，针对不同频率的响应，对比HVDC的准稳态模型和电磁暂态模型，可以更加准确地验证准稳态模型在HVDC稳定性分析中的适用性，尤其是在低频振荡和次同步振荡中的适用性。该方法可以进一步用于验证准稳态模型在大扰动情况下的有效性，同时也可以用于改进的HVDC准稳态模型和动态相量模型的验证。