耦合高效高精度水动力模型的多组分污染物输移及衰减反应模型

栾广学，侯精明，杨 露，李丙尧，郭敏鹏，杜颖恩，马 鑫

(西安理工大学省部共建西北旱区生态水利国家重点实验室，陕西 西安 710048)

随着我国城镇化进程快速发展，各类水环境问题相继浮现，尤其是突发污染事故频繁发生[1-4]，不仅对城乡居民的饮用水安全和生态环境造成了严重的影响，而且也影响了地区的经济发展[5]。如2012年三友化工污染门事件、2012年广西镉污染事件和2014年兰州自来水苯含量超标事件，对水市场、水环境产生了严重的影响，造成大量的生命财产损失。为有效应对各类水污染事故，及时预测污染事故严重程度并开展预报预警工作，对污染事故进行模拟显得尤其重要[6-10]。

在洪水演进及其伴随污染物输移模拟研究中，污染物的衰减反应与模型的计算精度和效率成为研究重点[11-12]。以计算机为依托构建数值模型，精确掌握水体有机污染物的输移及衰减反应规律，是当前研究自然水体水动力过程和水环境特征的重要手段[13-15]。目前，能够模拟水环境问题的水质模型有很多，如SWAT、SWMM和MIKE21 FM等[16]。张京等[17]应用SWAT模型对义乌江流域的径流、泥沙与水质过程进行了模拟。姚焕玫等[18]基于SWMM模型构建了南宁市区地表径流及非点源污染精细化雨水径流模型。李添雨等[19]采用MIKE21模型构建了沙河水库库区二维水动力水质模型，对沙河水库水量水质变化情况进行了模拟。以上模型均可对河流水库水质变化进行模拟，但模拟时存在输入地形网格精度低、计算效率不高等缺点[20]。李一平等[21]对地表水环境数学模型进行了系统的分析。陶亚等[22]以深圳湾为例对突发污染物事故的输移扩散规律和影响因素进行了模拟分析。龙岩等[23]采用HEC-RAS一维水动力水质模型对南水北调中线单组分水溶性突发污染事件的输移扩散规律进行了模拟预测研究。司鹄等[24]对三峡库区突发污染物的输移及衰减规律进行了模拟分析。以上研究主要为单一污染物的输移特性，且采用的大多为国外开发的商业软件，无法根据实际模拟对象对源代码进行修改调整。由此可见，能够对多组分水污染事故输移及衰减反应过程进行模拟预测的国内自主开发的模型还不够成熟。

国内自主开发的水动力水质模型对流域水质模拟时必须解决的关键问题是提高水质模拟性能和功能。基于以上模型对污染物输移过程模拟的不足，本文全面耦合基于图形处理器(graphics processing unit， GPU)加速技术的二维水动力模型与多组分污染物输移及衰减反应的Streeter-Phelps模型，建立一个可应用于复杂地形河道入流与溃坝洪水演进全过程与多组分伴随污染物输移及衰减反应的高性能耦合模型(GPU accelerated surface water flow and associated transport, GAST模型)，以期合理高效地模拟各类突发水污染事件并进行预警和评估。

1 数值模型及求解方法

1.1 二维水动力模型

GAST模型水动力模块控制方程为二维浅水方程[25]，主要针对具有自由液面且以平面运动为主的水流，只考虑水平方向流速，忽略垂向运动。忽略了运动黏性项、紊流黏性项、风应力和科氏力的二维非线性浅水方程守恒形式为

(1)

其中

式中：t为时间，s；q为变量矢量；h为水深，m；qx、qy分别为x、y方向的单宽流量，m2/s；F、G分别为x、y方向的通量矢量；g为重力加速度，m/s2；u、v分别为x、y方向的流速，m/s；S是源项矢量；i为入渗源项；zb为河床底面高程；Cf为谢才系数，Cf=gn2/h1/3，其中n为曼宁系数。

1.2 多组分污染物输移及衰减反应模型

污染物输移控制方程为二维对流扩散方程：

(2)

式中：C为污染物垂线平均质量浓度，mg/L；Dx、Dy分别为x、y方向的扩散系数；qin为点源排放的流量强度，m/s；Cin为点源的物质垂线平均质量浓度，mg/L；R为转化项，如污染物生化反应、生物作用等。

以BOD-DO耦合模型为例，仅考虑衰减与考虑生化反应情况时转化项R可分别表示为

R=k1ρ(BOD)

(3)

R=k1ρ(BOD)-k2D

(4)

其中

D=ρs(DO)-ρ(DO)

式中：k1为生化需氧量BOD耗氧速率，s-1；k2为溶解氧DO复氧速率，s-1；ρ(BOD)为BOD质量浓度，mg/L；D为氧亏值，mg/L；ρ(DO)为DO质量浓度，mg/L；ρs(DO)为饱和溶解氧质量浓度，mg/L。

1.3 数值方法

本文模型对水动力及污染物控制方程进行离散所采用的方法为基于Godunov格式的有限体积法，该方法保证了守恒性且能有效解决溃坝激波等非连续问题。采用可自动满足Godunov格式的HLLC近似黎曼求解器计算单元界面上的质量通量和动量通量以解决如冲击波等的间断问题[26]。通过静水重构来实现干湿边界处全稳条件，采用格式自适应方法来保障干湿交替过程模拟的稳定性。为达到复杂地形上的全稳条件，底坡源项使用底坡通量法处理复杂地形引起的动量不守恒问题。采用TVD-MUSCL方法进行数值重构，并采用两步Runge-Kutta法进行时间步长的推进，以保证时间积分的二阶精度[26]。离散网格类型为均匀结构网格。采用水深变化和水深值共同作为判别条件，以有效解决复杂地形干湿界面处的负水深和极端高流速等非物理现象所造成的计算失稳和物质动量的不守恒等问题。为提高模型的计算效率，通过CUDA语言自主编程实现GPU并行计算，以达到高速运算的目的[27]，图1为GPU加速计算流程图。

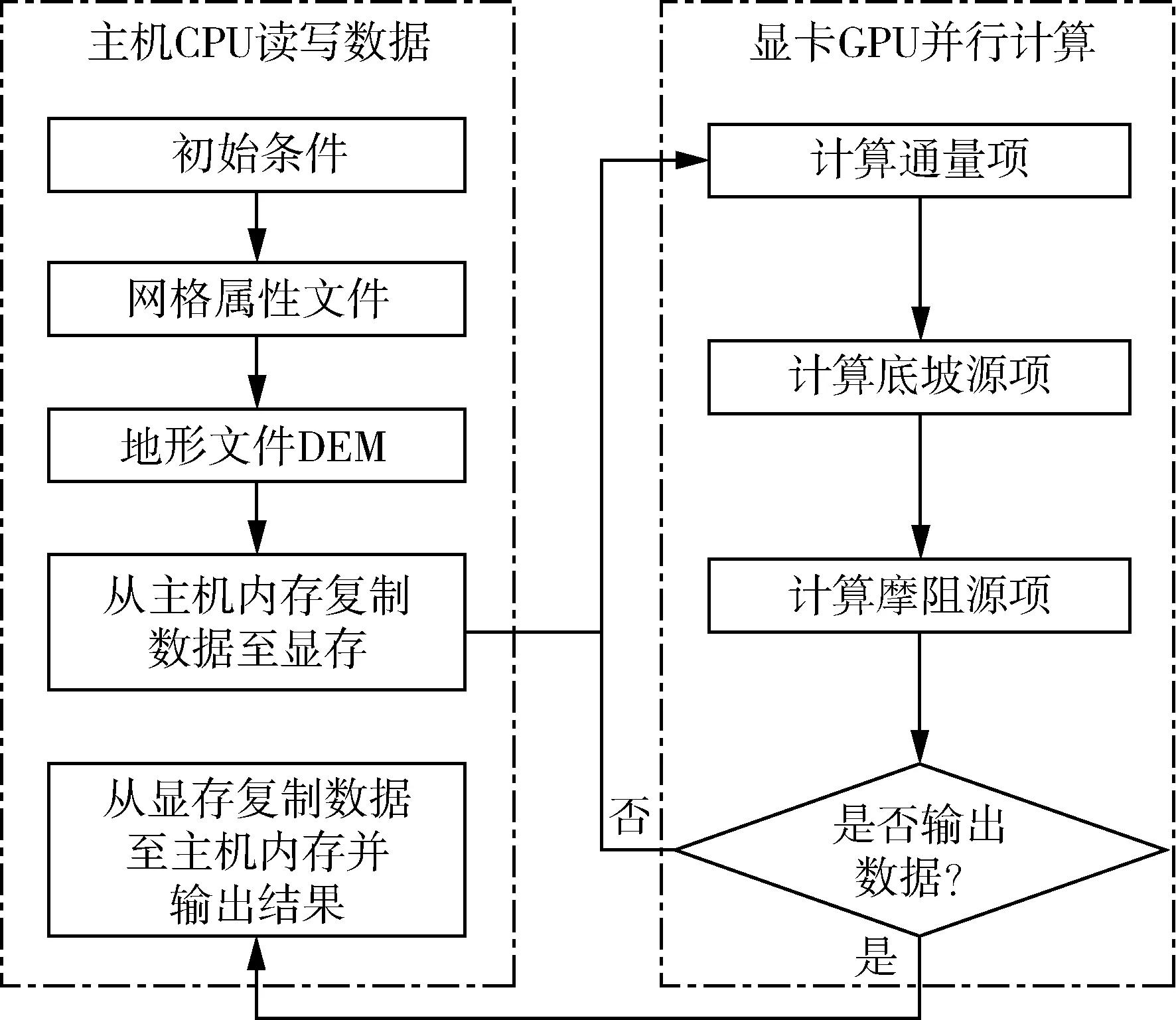
图1 GPU加速计算流程Fig.1 GPU accelerated calculation flowchart

2 模型验证

为验证污染物输移及衰减模型的计算精度，本文通过建立理想地形算例对污染物衰减的数值解与解析解进行对比分析，模型处理扩散项的合理性已得到充分验证[28]，故模型验证忽略污染物的扩散项，仅对模型的衰减过程进行验证。构建一个边长为50 m、底坡为0的正方形作为理想地形，以验证模型在静水状态下的污染物衰减过程。

2.1 解析解

式(3)与(4)中反应项R可看作水质变量的质量浓度对时间的全导数，DO与BOD的反应项形式为

(5)

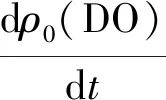
(6)

其边界条件为：在x=0处，ρ(BOD)=ρ0(BOD)，ρ(DO)=ρ0(DO)，D=D0。因数值模拟时间步长很短，因此对上述反应项使用有限差分法求解可得一个步长内的解析解形式为

ρ(BOD)=ρ0(BOD)-k1ρ(BOD)dt

(7)

ρ(DO)=ρ0(DO)-k1ρ0(DO)dt+k2ρ0(DO)dt

(8)

式(7)为单组分衰减模型解析解，式(7)与(8)为多组分衰减反应模型解析解。

2.2 单组分衰减模型

单组分衰减模型验证算例四周均为固壁边界，点源污染物设置在x=25 m、y=25 m处，质量浓度为1 mg/L、初始水深为1 m、衰减系数取0.1，计算点源污染物质量浓度的衰减变化，计算时长为50 s。图2为点源中心位置单组分污染物质量浓度在线性衰减情况下的变化趋势。结果表明：在线性衰减情况下，污染物质量浓度随时间的推移逐渐降低，因其与自身质量浓度有关，因此在污染物衰减速率不变时衰减量随污染物质量浓度的减小而减小；单组分污染物质量浓度的衰减过程数值解与解析解基本吻合，无明显数值震荡现象，表明模型稳定性好且精度高。

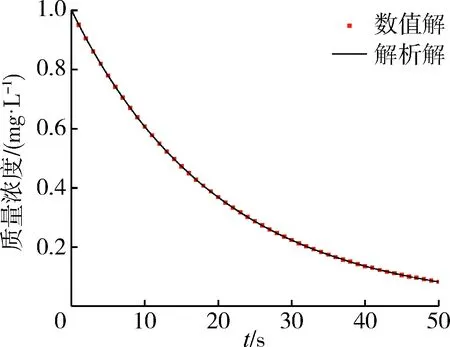
图2 单组分污染物质量浓度衰减变化过程Fig.2 Change process of attenuation of single-component pollutant concentration

2.3 多组分衰减反应模型

多组分衰减模型验证算例采用BOD和DO两种污染物组分耦合模型，忽略纵向离散作用，且不考虑饱和DO质量浓度对复氧速率的作用。多组分点源污染物位置设置在x=25 m、y=25 m处，将BOD和DO初始质量浓度均设置为1 mg/L，水深为1 m，BOD耗氧系数取0.05，DO复氧系数取0.02，计算多组分点源污染物质量浓度的衰减反应变化，计算时长为50 s。

静水流场中多组分污染物衰减反应模拟结果对比与数值解及解析解部分计算结果如图3所示。由图3可见，在忽略对流项与扩散项的情况下，BOD和DO相互反应的数值解与解析解在模拟时间内的任何时刻相对差值均极小。计算得出，BOD数值解与分析值的相对误差为1.8%；DO数值解与解析解的相对误差为1.0%。显然，模型模拟多组分污染物的数值模拟结果与理论值相比偏差较小，在允许范围内，具有较高的稳定性和精度。模型实现了多组分污染物衰减反应功能，BOD的质量浓度逐渐降低且衰减速率逐渐变缓；DO质量浓度在26 s之前降低且衰减速率逐渐变小，在26 s达到转折点，随后其质量浓度开始回升，且回升速率逐渐增加。本算例BOD质量浓度的衰减只与其自身质量浓度有关，不受DO质量浓度影响，且为线性衰减，故其质量浓度逐渐降低且总量衰减速度逐渐变缓；DO质量浓度的变化受BOD质量浓度的影响且其复氧速率与其自身浓度有关，BOD质量浓度较大时，其耗氧速率较DO的复氧速率大，故DO质量浓度降低，因BOD耗氧速率比其自身的衰减速率小，因此随着BOD质量浓度的减小，其耗氧速率逐渐接近DO的复氧速率，并且在26 s时刻相等，DO质量浓度到达最低值，随后BOD质量浓度继续降低，耗氧速率越来越微弱，故复氧速率逐渐占主导地位，DO质量浓度开始回升且回升速率越来越快。

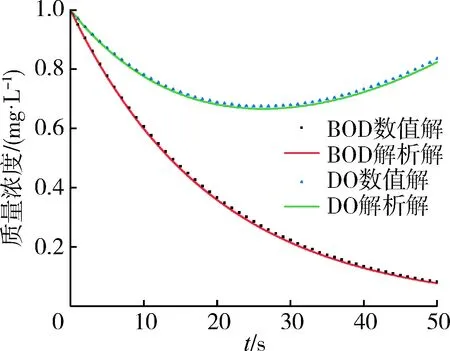
图3 静水流场中多组分污染物相互反应的数值解与解析解对比Fig.3 Comparison of numerical and analytical solutions of multi-component pollutant interaction in static water flow field

3 Toce河道多组分点源输移及衰减过程模拟

对Toce河道上释放的多组分点源污染物输移及衰减过程进行模拟，河道DEM数据分辨率为0.05 m，网格单元共计206 640个。河道数字地形高程如图4所示，左边界为入流口，入流宽度设置为3.4 m，右边界为自由出流的开边界，其余为闭边界。入流流量过程线如图5所示，河道曼宁系数取0.016 2 s/m1/3，初始水深设为0 m，点源位置设置在x=7.868 m、y=5.882 m处，如图4所示。点源同时释放两种污染物，用C1和C2表示，排放质量浓度为1 mg/L，强度为0.8 m/s，设置C1衰减系数为 0.3 s-1，C2无衰减，污染物随水流向下游推进。

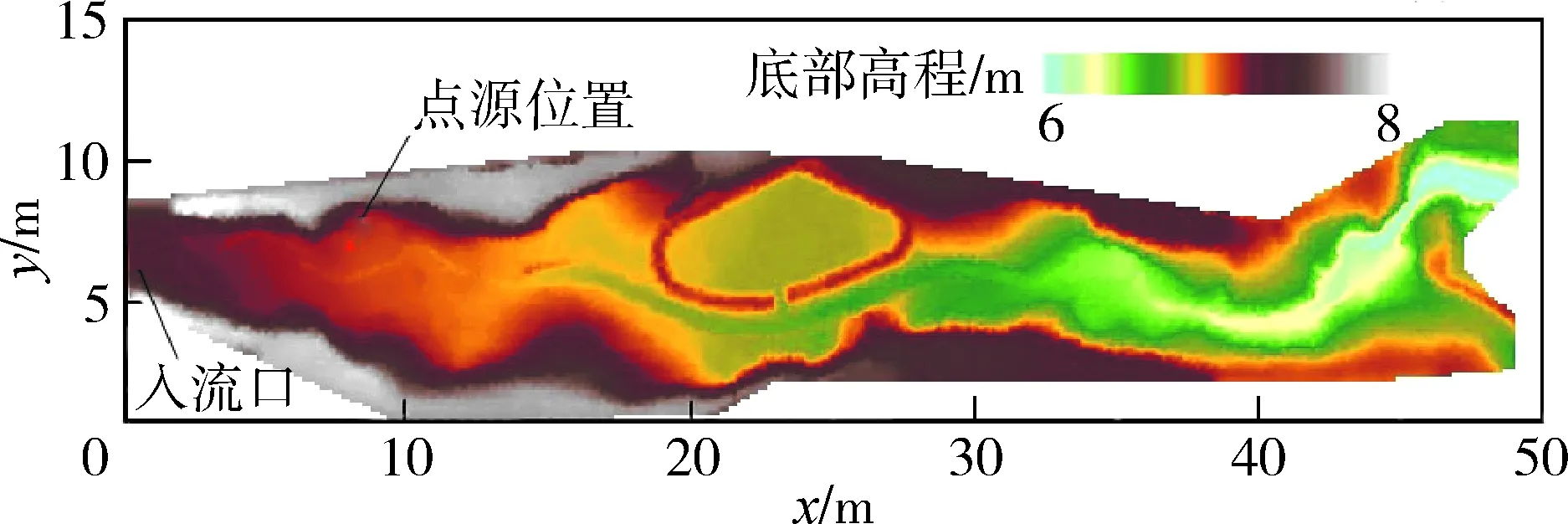
图4 Toce河道数字地形高程及点源位置Fig.4 Digital terrain elevation and point source location of the Toce River

图5 入流流量过程线Fig.5 Inflow hydrograph

采用本文模型模拟计算3 min内的水流演进及其伴随污染物输移及衰减过程。在t=20 s和t=50 s 时的水深模拟结果如图6所示，污染物有衰减与无衰减输移在t=20 s，40 s，60 s、80 s时的质量浓度分布情况如图7所示，多组分污染物在x=11.125 m、y=5.825 m处的有衰减与无衰减过程质量浓度对比如图8所示。

(a) t=20 s

由图6可知水流向下游推进速度很快。图7表明，在t=20 s时水流即流过点源位置，污染物随着水流向下游推进，质量浓度逐渐降低。在t=40 s时，污染物随水流向周围低洼处输移；在t=60 s时，部分水流进入旁侧低洼区，污染物随水流开始分流；在t=80 s时，污染物即将随水流从河道下游边界流出，污染物C1随水流迁移过程中因自身的衰减，质量浓度明显低于无衰减情况，C1到达下游出口位置时间明显较C2延后。图7也显示了污染物在点源位置释放并向下游输移的整个过程，污染物分布与干湿界面相匹配，在复杂地形的河道内始终随水流向下游输移，由此表明：点源污染物排放不仅会造成严重的水体污染，而且对下游水体的影响很大。图8表明，在x=11.125 m、y=5.825 m处，C1的质量浓度始终低于C2的质量浓度，由于复杂地形河道的影响，C1与C2的质量浓度差值呈不规则趋势。

(a) 无衰减，t=20 s

图8 多组分污染物有衰减与无衰减输移过程质量浓度对比Fig.8 Comparison of concentrations of multi-component pollutants with and without attenuation

4 Malpasset溃坝多组分点源输移及衰减过程模拟

本节模拟计算Malpasset河道溃坝水流运动及其伴随污染物的输移、衰减过程。河道数字地形高程如图9所示，网格精度为10 m，网格单元共计 1 581 714 个，坝前水位设置为100 m，多组分点源污染物排放口设置于x=5.257 km、y=6.685 km处，如图9所示，排放质量浓度为1 mg/L，强度为1 m/s，河道曼宁系数取0.016 2 s/m1/3，点源同时释放两种污染物，用C3和C4表示，点源排放质量浓度为 1 mg/L，强度为0.8 m/s，设置C3衰减系数为 0.000 1 s-1，C4无衰减。图10为t=300 s和t=1 800 s时的水深分布，图11为污染物无衰减与衰减输移(t=300 s，1 500 s，3 000 s)质量浓度分布。

图9 Malpasset河道数字地形高程及点源位置Fig.9 Digital terrain elevation and location of point source of the Malpasset River

由图10可见，溃坝发生后，水流迅速向下游推进。由图11可见，多组分污染物随溃坝水流向下游推进，1 500 s时即到达下游位置。河道下游C3的质量浓度明显小于C4的质量浓度，由此表明污染物因其自身的衰减反应，随水流到达下游时，质量浓度削减效果明显。本文模型在GTX1080计算机上运行0.37 h即可完成2 h水流及污染物输移、衰减反应过程模拟。

(a) t=300 s

(a) 无衰减，t=300 s

5 结 语

本文将基于GPU加速技术的二维水动力模型与多组分污染物输移及衰减反应模型进行耦合，构建了一个可应用于复杂地形河道入流与溃坝洪水演进全过程与多组分污染物输移及衰减反应的高性能耦合模型。模型实现多组分污染物输移、衰减反应模拟功能，适用于大区域复杂地形河道的水质模拟；引入GPU加速技术提高了模拟效率，计算1 581 714个均匀结构网格2 h的溃坝及污染物输移、衰减反应模拟，仅需运行0.37 h。

通过对理想地形及两个复杂地形河道的水质模拟，结果表明，模型计算结果与解析解基本吻合，在入流与溃坝算例中的模拟结果符合实际的物理过程，运行速度快且计算效率高，具有较好的鲁棒性，能高效地模拟各类水污染事件并进行预警和评估，可为敏感水域水环境的治理和保护提供技术与数据支撑。