基于广义向量模长的食品安全风险评价体系
王建新,李腾旭,李中天,王晔茹
(1 北京林业大学信息学院 北京 100083 2 国家林草局智能信息处理中心 北京 100083 3 国家食品安全风险评估中心 北京 100022)
诸多发达国家已经把食品安全问题提升到国家安全的战略高度[1]。我国也十分重视食品安全问题,已把食品安全上升至与国防安全同等重要的重大民生工程之一[2]。而食品安全评价是实现食品安全管理的前提和首要条件,它对食品的安全性给出判断性描述,最终是一个分类和等级评价的问题,这是目前研究的热点和难点。由于食品安全风险评价是其它食品安全管理活动的前提和基础,能为食品安全管理部门提供决策辅助[1],也能为社会大众提供食品安全的知情权,因此是食品安全管理的关键环节。公平公正、科学合理的评价体系使得后续的风险管理、预警和响应机制有章可循、有据可依。
食品安全风险评价体系的主要议题有4 个,这都是当前研究的热点。第一是建立指标体系,即评价体系中应该包含什么指标,它们的组织结构是什么。第二是权重设置,即设置各个指标在评价体系中的数量化的重要程度。第三是指标值到分值的映射关系。由于一般的评价结果最终是分值或等级这样的数量值,因此,需要把指标中类别化的或数量化的取值映射为分值或等级值。第四是分项分值到总项分值之间的汇总合成关系。由于指标体系中总项会由若干个分项构成,而每个分项又可能会有若干个更细的分项构成,因此需要建立分项分值到总项之间的汇总合成映射关系。有时这种合成汇总关系比较简单,包括简单的加权相加、求均值等,有时按照实际需要会非常复杂。
要进行食品安全评价,首先需要建立合理的指标体系。指标体系分为单层指标体系和多层指标体系。在单层指标体系中,决定食品安全风险综合程度或指数的是若干个变量,这些变量之间的关系是平行的,它们或者是等权重的,或者是非等权重的,所有变量的分值最终决定综合的食品安全风险程度。为建立乳制品安全风险评估指数,有研究[3]选取了14 个指标,用3 种综合评价法施加于这14 个指标,结果具有高度一致性,验证了指标选取的合理性。吕学东等[4]构建了出口食品生产企业“三同”成熟度评价体系,也是典型的单层评价指标体系,文中通过百分制给每个指标赋予了一个权重,通过加权得分评价一个企业的“三同”成熟度。
然而,在食品安全评价中,单层评价指标体系相对较少,这是因为食品安全评价是一个复杂的系统工程,因此多层指标体系在文献中更为常见,也更为频繁地在实践中使用,常见的层次分析法(AHP 法)也是典型的多层结构。AHP 法是由美国匹兹堡大学的运筹学教授萨蒂提出的一种定性与定量结合的多层权重分析方法,该方法把一个复杂问题先看作一个整体,然后逐层分解,一个高层的目标可以分解为若干个低一层级的目标[5]。
建立指标体系之后,需要为各个指标设置权重,方能通过指标变量的值计算风险得分。设置指标权重通常分为主观设定和客观计算两种方式,有时也会把二者结合起来操作。有研究[4]由专家直接给出各个指标的权重值。然而,AHP 法中的权重一般由若干个专家分别给出,收集专家给出的权重分值后,需要进行一致性验证[5]。如果验证通过,就说明专家们对权重的分配达成基本一致的意见,权重保留;否则,需要专家重新对权重进行分配。除了采用层次分析法[5-6]外,多个应用中用层次分析法建立指标体系和设置权重,包括对农副产品供应商的评价体系研究[7],对基于供应链的区域性食品安全状况的评价[8],对食品生产企业质量安全的评价体系研究[9],以及对我国食品企业信用评价体系的建设[10]等。AHP 法中的权重设置是典型的主客观相结合的方法。熵权法通过指标数据确定指标的权重[11-13],是纯粹客观的权重设置法,然而,前提条件是各个待评价的对象在每个指标变量上的取值已经全部获取,因此该方法的适应性较弱,对一些指标值超出已知数据范围的新对象无法评价。主成分分析方法也是一种客观设置权重的方法,其利用历史数据,通过各指标的线性贡献判定指标权重。例如,研究[3]利用主成分分析方法实现了乳制品安全风险评估指数中的权重设置。
在建立指标体系、设置各指标权重后,需要建立指标值到分值的映射关系,映射关系建立的方法有很多种,如等级离散划分法[2],把评价结果值区间[1,5]划分为5 个安全等级,包括“很差”“很好”等,例如后者的评价值区间可以是(4.2,5]等。而为了度量哪些变量会影响消费者举报网络外卖餐饮店的食品安全违法违规行为,王浩等[14]自定义了若干个原因变量,这些变量大部分都是5 等级取值的。更多使用的是指标值到得分值之间的线性映射,如采用线性映射[15]计算低碳生产、经济增收、安全供给等方面的绿色发展指数,最后综合计算总体的绿色发展指数。
食品安全风险评价体系中另外一个重要的议题就是建立分指标项(分项)分值到总指标项(总项)之间的汇总合成映射关系。不管是单层指标体系[3],还是多层指标体系[4-10],总项分值是n 个分项分值的线性加权和,如公式(1)所示。

式中,T——总项分值;vi——各分项分值;αi——各分项权重,i=1,2,…,n,且要满足αi=1。
1 分项到总项的映射关系
除了线性映射外,分项到总项分值的映射方式可以有多种,可以更复杂,而不仅仅限于公式(1)这种映射方式。更一般的形式如公式(2)所示。
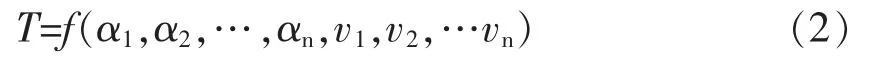
式中,f——任意的线性或非线性映射。
虽然线性映射方式在分项到总项的映射中比较常用,但是它存在一个重要缺陷。在食品安全风险评价中,如果某个分指标的分值较高,即风险较高,则会认为总指标中存在这样一个“短板”:即使其它分指标的数量很多,风险都比较小,也不能把总指标判定为低风险。也就是说,在风险评估和评价中,分值较高的分项的影响较大,分指标的分值不适合按照权重线性相加。
食品安全风险的大小,以及它对监管部门和舆情的影响,并不简单是各个因素严重程度的加权和,而是更偏重于突出事件、出现严重问题的因素或分指标。实现这一映射关系的传统做法是使用模糊隶属度函数(简称为模糊函数)。例如,公式(3)是一个简单的模糊函数,也称为最大模糊算子:

根据公式(3),总指标分值(代表总体风险)是分指标分值的最大值。也就是说,总指标风险值由分指标风险值中最大的那个决定。这个映射关系比较符合人们对风险的认知:系统风险由系统中的短板决定。有研究应用模糊综合[16]的方式对高校食堂的食品卫生做了评价和分析,易于发现食堂食品卫生的短板问题,以便督促改进,有研究应用更一般的三角模糊法[12]评价冷链货架周期,然而,通过施加三角模糊的运算法则,最终的映射结果仍呈现为非此即彼的形式。还有研究[11]首先用熵权法确定分指标的风险分值,然后也通过模糊综合的方式获得总指标的风险分值。
另一方面,与风险评估评价相反,若要对安全性进行评价,计算安全指数等,则分指标的安全值中最小的那个对总指标具有决定作用,这也是一个模糊函数,称为最小模糊算子:

公式(4)的意义是:总指标的安全性由最不安全的分指标决定。
然而,上述模糊评价的方式存在另一个重要的缺陷,即总指标的分值必须是某一个分指标的分值,非此即彼,具有排他性,并不满足实践应用中的需求,也就是严格单调性范式要求。所谓严格单调性范式要求是:对于两个评价对象,若除第k个分指标外,其它分指标的值都相同,则两个对象的总指标值相对于第k 个分指标的值要满足严格单调性。严格单调性包括严格单调增和严格单调减。这里以严格单调增为例,形式化地描述严格单调性范式要求。
假设两个待评价对象O'和O″在n-1 个分指标上的分值都相同,而在第k 个分指标上的分值不同,也就是二者的分指标值分别是:S1,S2,…Sk-1,Sk',Sk+1…Sn和S1,S2,…Sk-1,Sk″,Sk+1…Sn,且假设Sk'>Sk″,那么严格单调增范式要求需要两个总指标的分值满足Tk'>Tk″,然而,最大模糊算子和最小模糊算子显然都不满足严格单调范式要求,会出现Tk'=Tk″的情况。例如,假设两个待评价对象O'和O″只有两个分指标,它们的分值向量分别是(0.3,0.8)和(0.4,0.8)。根据最大模糊算子,这两个待评价对象的总指标分值都是0.8,显然不满足严格单调性范式要求。事实上,就风险而言,O″比O'风险更高,二者风险值不应该相等。同理,对最小模糊算子也存在大量不满足严格单调性范式的例子。
模糊评价方式虽然突出了重点分指标对总指标分值的决定作用,但是完全忽略了其它分指标对总指标分值的影响,在逻辑上并不合理,在实践应用中是有缺陷的。
为了融合和兼顾重点分指标对总指标的决定性影响和严格单调性范式两个要求,需要新的映射方式,为此,作者提出广义向量模长的映射方法,并从数学证明和实践应用两个角度说明其优势。
2 数据与方法
2.1 欧式向量模长映射方法
有研究[12]采用欧式距离比较两个商品的货架期差异,并取得良好的效果。两个商品的欧式距离由分项计算,如公式(5)所示:

借鉴这个距离定义,可以建立基于欧式模长的分指标值到总指标值的映射方式,即通过计算分指标值构成的向量与0 向量的距离获取总指标的分值,如公式(6)所示:

显然,欧式向量模长的映射方式是符合严格单调范式的(证明略)。另外,该评价方式也满足重点分指标对总指标的决定性影响的要求。例如,假设食品安全风险由4 个因素构成,其分值分别是v1,v2,v3,v4,各因素的权重均为0.25,对于某食品,前3 个分指标的分值都是0.1,第4 个分指标的值是0.9,则按照线性加权和映射方式,综合风险的分值是0.25×0.1+0.25×0.1+0.25×0.1+0.25×0.9=0.3。用欧式向量模长的方式可以做如下计算:

欧式向量模长的映射方式也有其不足之处。从公式(7)的例子可以看出,突出的分值对总指标的影响程度是固定不变的,因此,欧式模长不具有普适性,不能随需要而调整,究其关键原因是由于该评价方式没有可调整的超参数。另外,公式(7)所示欧式模长评价方式没有考虑各个分指标的权重,需要在欧式模长的基础上提出更普适的映射方式。
2.2 广义向量模长映射方法
定义从分指标值到总指标值的广义向量模长映射方式如公式(8)所示:

式中,β——超参数,取值范围可以从负无穷(包括)到正无穷(包括);αi——各个分指标的权重,i=1,2,…,n,且要满足广义向量模长的广义性体现在两个方面:第一,该模型具有超参数β,有更广泛的适应性;第二,与欧式模长映射方式不同,它兼顾了各个分项的权重值。
首先,证明如下有关渐近性的命题:
命题1.当超参数β 趋于正无穷时,广义向量模长映射退化为最大模糊算子映射。
证明:为了证明过程的简洁,先假设共有2 个分指标(有更多分指标时,证明过程类似),也就是n=2,两个分指标的值分别是v1和v2,且v1>v2。

从上面的证明结果可以看出,经过广义向量模长映射,总指标值就是分指标的最大值。这种映射实际上就是最大模糊算子映射。
命题2.当超参数β 趋于正0 时,广义向量模长评价方式退化为几何加权平均。

根据洛必达法则,上式分子分母同时求导:

因此,

公式(9)其实是几何平均的一般形式。特殊地,当α1=α2=0.5 时,

上式恰好是各个分指标值传统意义上的几何平均。下面通过一个例子比较算术平均映射和几何平均映射。仍然假设有2 个分指标,每个分指标所占权重都是0.5,两个分指标的值分别是0.3 和0.9,那么它们的算术平均值是0.6,然而,几何平均值是0.5196,二者虽接近,但又有不同,几何平均映射的结果更接近于分指标中较小的值。
命题3.当超参数β 趋于负无穷时,广义向量模长评价方式退化为最小模糊算子。
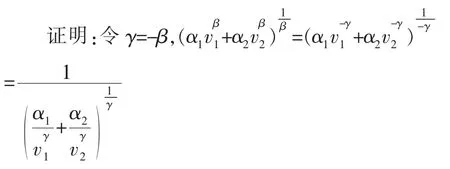

于是有,

因此,
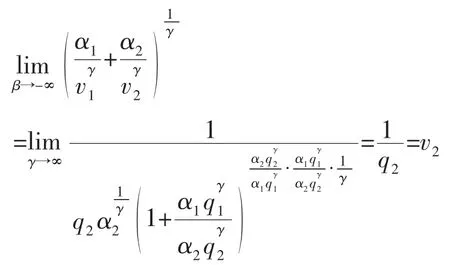
所得结果即为分指标中的最小值。这说明,当超参β 趋于负无穷时,广义向量模长映射即最小模糊算子映射。
2.3 广义向量模长映射方法的超参取值区间
公式(8)表示广义向量模长映射方法,其超参β 在正无穷、0、负无穷处均没有定义,除此之外,在实数轴上的任何其它地方都有定义,可计算。为此,前文通过求极限的方式,重新在这3 处给出了公式(8)的扩展定义,使得公式(8)的超参β 在包括正、负无穷的整个实数轴上都有了定义。进一步地,通过前文的证明,可以得出:广义向量模长映射方法能够涵盖前述的几乎所有的映射方法,包括最大模糊算子法、最小模糊算子法、欧式模长法、算术平均法、几何平均法,也包括这些方法之间的过渡状态方法。广义向量模长映射法随着超参β 的变化,与其它映射方法的关系如图1所示。

图1 广义向量模长映射法与其他映射方法的关系Fig.1 The relationship between generalized vector modulus length mapping method and other methods
首先,超参β 的值越大,映射结果就越接近于分指标项中的最大值。极端情况,当β 为正无穷时,映射结果即分指标项的最大值。相反地,超参β 的值越小,映射结果就越接近于分指标项中的最小值。极端情况,当β 为负无穷时,映射结果即分指标项的最小值。特殊地,当β 的值为0,1,2时,广义向量模长映射法分别退化为几何平均映射法、算术平均映射法和欧式模长映射法。
除了超参β 在正负无穷的极端情况,广义向量模长映射方法均满足严格单调范式。
除了上述特殊情况,超参β 在过渡状态情况下的映射方法更有意义。当β 位于区间(1,+∞)中时,映射结果会更偏向于较大的分项值,并且随着β 的增加,这种偏向的程度更深。当考虑风险指数等综合指标时,可以让超参β 选择这个区间的值。相反地,若考虑安全指数等指标,则可让超参取值在区间(-∞,0)中。超参β 在这个区间中时,映射获得的总指标的值更倾向于各个分指标的最小值,并且随着β 的减小,这种倾向性就更明显。当超参β 在区间[0,1]中时,既可以映射风险指数,也可以映射安全指数,然而,由于不能很好地体现关键子指标对总指标的决定作用,因此建议尽量不采用。不过,当要把分指标信息尽量完整地反映到总指标中,而又不考虑分指标值的大小对映射方式的影响时,可以考虑用这个区间中的超参值。与众多文献中的映射方式类似,可以让超参β 取值为1,这时广义向量模长映射法就退化为线性加权平均法。
由于广义向量模长映射法完全由超参数β 决定,因此,用Gβ表示一个特定的映射方法。例如,G10表示超参为10 的广义向量模长映射法,G∞就是最大模糊算子映射法。
3 结果与分析
3.1 超参数对映射关系的影响实例
根据广义向量模长的公式(8),表1列出部分超参数对总指标分值的影响程度。这里仍然假设只有两个分指标,其权重α1=α2=0.5,且分项值v1=0.9,v2=0.2。根据广义向量模长的公式(8),以及它在一些特殊点上的扩展定义,得到对应关系,见表1。
从表1可以看出,随着超参数β 从正无穷变化到负无穷,总指标项的值从分指标的最大值逐渐变化为分指标的最小值。在实际应用中,可以参考表1中的数据,按照实际需求,选取合适的映射关系,即选取重要值的分指标对总指标的合适的影响程度。也可以根据实际需求,选取表中两个相邻超参之间的某个中间值。

表1 广义向量模长方法中超参数对总指标分值的影响关系Table 1 Impact of the hyper-parameter to total metric score in the method of generalized vector modulus length
3.2 广义向量模长映射法的应用
为了评估兰州市柑橘类水果的农药残留风险,文献[17]建立了指标体系,其中包括甲拌磷等6 个分指标。本文把广义向量模长映射法应用于这个评价案例,验证该方法的有效性。比较结果如表2所示。

表2 广义向量模长映射法与其它方法的应用比较Table 2 Application comparison between the method of generalized vector modulus length and other methods
观察表2中线性加权映射法(G1),它的最终结果与分指标最大风险值0.8 相差甚远,因此不能反映具有重要值的分指标对总指标的决定作用。相反地,最大模糊映射法(G∞)和广义向量模长法(G10)的结果都是或比较接近分指标的最大值,符合实际情况,更有应用价值。
然而,最小模糊映射法(G-∞)在所有情境中的结果都是0,因此在考虑风险指数而不是安全指数时,不具有应用价值。相反地,在考虑安全指数计算时,该方法会更为实用。
情景1 和情景2 的6 个分指标风险值除了“苯醚甲环唑”外,全部相同,广义向量模长映射法(G10)捕捉到这个差异,总指标的风险值也有所不同,且满足严格单调性范式。然而,最大模糊映射法(G∞)不具备捕捉这个差异的能力,其最终的风险值均为0.8,与分指标的最大值完全相同。
两个分指标“敌敌畏”和“苯醚甲环唑”的权重不同,在情景2 和情景3 中交换了风险值,这在线性加权映射法(G1)中得以体现,从情景2 的0.32变化为情景3 的0.23,在广义向量模长映射法(G10)也得以体现,从情景2 的0.70947 变化为0.63661,而最大模糊映射法(G∞)不具备捕捉这个变化的能力,它对权重的变化并不敏感。
综上分析,广义向量模长映射法从各个角度看,具有比较大的综合优势。
4 结论
食品安全风险评价体系的科学合理性和公平公正性对食品安全管理具有重要作用,是其不可或缺的组成部分。好的评价体系能够使食品安全监督检查有据可依,可以更好地区分食品企业和食品产品,结合监督抽检和检验检查等起到引导和督促的作用。评价体系建设的第4 个议题(由分到总的映射)中,存在不能体现重要分指标值对总指标值的决定作用、不满足严格单调性范式等问题。本文提出的广义向量模长映射法不但能够很好地体现重要分指标值对总指标值的决定作用,而且能够满足严格单调性范式。更重要的是,通过严格的数学推导,证明广义向量模长映射法是传统映射方法的统一形式,可通过超参的选取,确定适合应用场景的广义向量模长映射实例。通过实际的应用场景,验证了这些结论。
在多层的指标体系中,存在多次的从分指标值到总指标值的映射过程,需要有多个超参β。一般来说,同一个指标体系下的超参不要求统一,应根据实际需求,决定不同映射关系中的不同超参的值。
虽然提出广义向量模长的分指标值到总指标值的映射方法,但是指标体系建设中仍然存在诸多问题和难点,后续将把映射方法与另外3 个议题结合,形成有机统一的指标体系方法论和建设指南。

