无底柱分段崩落法采场结构参数：发展现状、确定方法及存在的问题*

谭宝会，胡颖鹏，张志贵，李明润，贾凯跃，梁 博，鲁 旭

(西南科技大学 环境与资源学院，四川 绵阳 621010)

0 引言

无底柱分段崩落法自20世纪50年代起源于瑞典Kiruna铁矿以来，因其具有机械化程度高、生产效率高、采矿成本低、安全性好以及应用灵活等优点，而被迅速推广至世界各地[1-3]。该采矿方法于1965年引入我国以后，被广泛应用于国内地下金属矿山(尤其是地下铁矿)的开采中。尽管无底柱分段崩落法具有一系列显著优点，但由于该采矿方法是在覆岩下出矿，崩落的矿石与覆盖层废石直接接触，易导致矿石贫损增大，这是其最大的缺点[4]。前人研究发现，无底柱分段崩落法的矿石贫损与采场主要结构参数(指分段高度、进路间距以及崩矿步距)的取值及其配比关系密切相关[5]。因此，为了获得更好的矿石回收效果，学者们通过物理实验、数值实验以及现场实验等方法对无底柱分段崩落法的合理采场结构参数进行了大量研究。此外，近年来随着采矿机械设备的不断更新以及矿山企业对进一步提高采矿效率和降低采矿成本的需求日益迫切，在很大程度上推动了无底柱分段崩落法采场结构参数研究的快速发展。

本文调研了当前国内外无底柱分段崩落法矿山采场结构参数的研究现状，总结了目前常用的采场结构参数确定方法，在此基础上指明了无底柱分段崩落法采场结构参数的确定原则，最后探讨了确定最优采场结构参数时存在的一些问题，以期为无底柱分段崩落法矿山采场结构参数的确定和优化提供借鉴。

1 无底柱分段崩落法采场结构参数发展现状

1.1 无底柱分段崩落法采场结构形式

采用无底柱分段崩落法进行采矿时，采场内的回采进路需要严格遵守上下分段菱形交错布置的原则，主要的采矿工艺环节如中深孔凿岩、装药爆破及铲装运输均在回采进路内完成，图1展示了典型的无底柱分段崩落法采场结构形式。由图1可以看出，在无底柱分段崩落法采场中，分段高度(H)、进路间距(B)和崩矿步距(L)这3个结构参数与采矿生产息息相关。

1、2-上下阶段沿脉运输巷道；3-矿石溜井；4-设备井；5-通风行人天井；6-分段运输平巷；7-设备井联络道；8-回采进路；9-分段切割平巷；10-切割天井；11-上向扇形炮孔。

由于无底柱分段崩落法特殊的菱形采场结构形式以及端部出矿方式，在各回采单元(步距、进路、分段)回采结束后会有脊部残留、靠壁残留和正面残留等残留矿石产生(见图2)，使得采场中的部分矿石具有转段或转步距回收的特点，即“前面留、后面收，上面丢、下面捡”，但矿石残留不等于矿石损失。因此，采用无底柱分段崩落法欲获得满意的矿石回收效果，就要使分段高度、进路间距和崩矿步距这3个主要结构参数之间构成较为合理的配比关系，从而使采场中的“崩落矿石堆体+残留矿石堆体”的形态最大限度地与放出体的椭球形态相符。这3个结构参数除了会影响矿石回收效果以外，还直接关系到无底柱分段崩落法的采矿成本、采矿效率以及作业安全性等。因此，对于一个无底柱分段崩落法矿山而言，采用合理的采场结构参数是非常重要的。

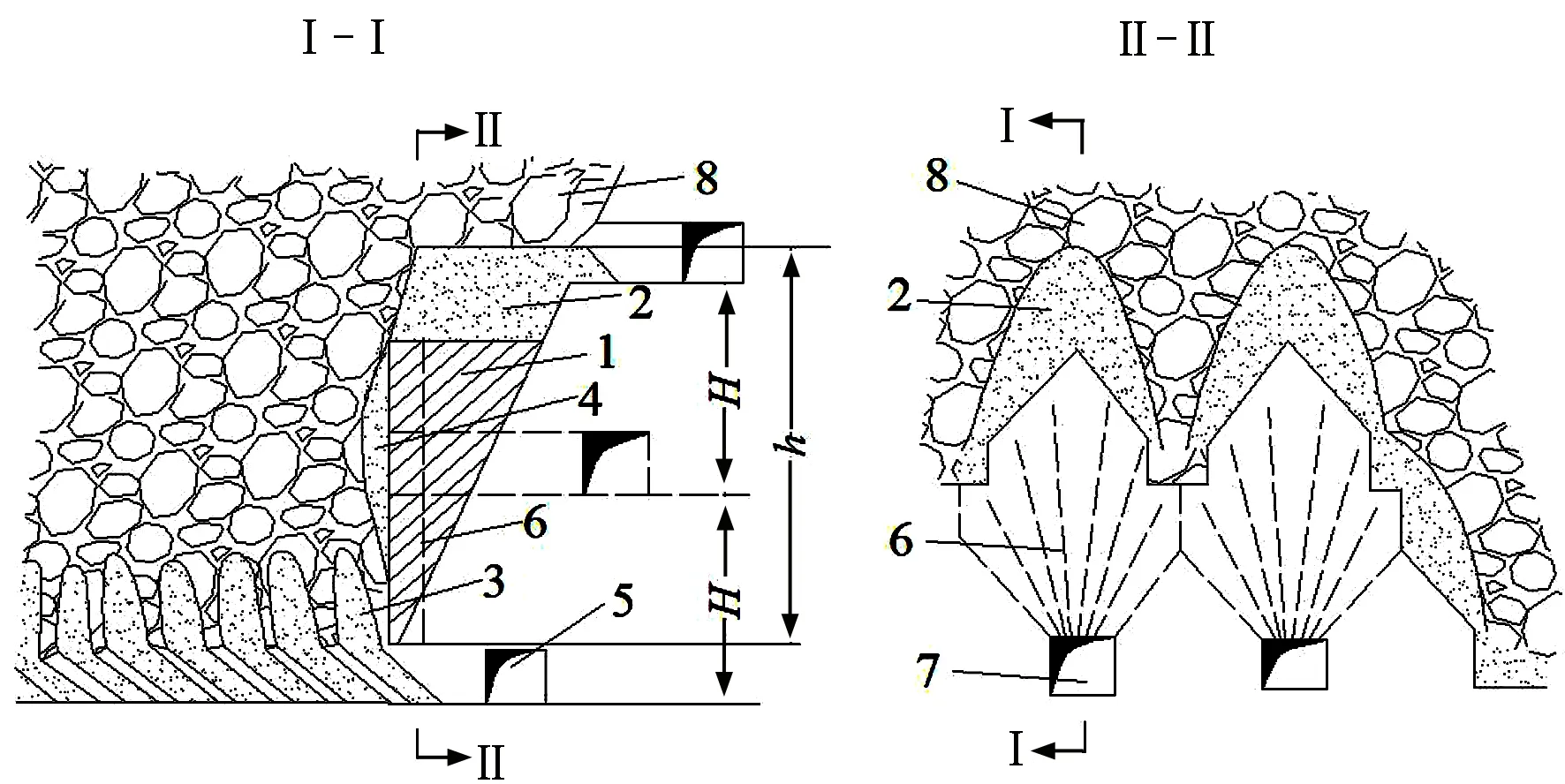
1-下盘矿石残留；2-脊部矿石残留；3-正面矿石残留；4-靠壁残留；5-下盘联巷；6-炮排；7-回采进路；8-覆盖岩层；H-分段高度；h—放矿层高度。

1.2 无底柱分段崩落法结构参数发展历程

随着无底柱分段崩落法的采矿技术、放矿理论以及配套采矿设备的迅速发展，近几十年来国内外无底柱分段崩落法矿山的采场结构参数不断发生变化。表1给出了瑞典Kiruna铁矿采场结构参数的演变历程。从表1可以看出，该矿基本上每隔10～20 年便会经历一次较大的采场结构参数变革，经过近70年的发展，其采场结构参数已从最初的7.5 m×7.5 m×1.0 m(H×B×L)发展到当前的28.5m×25.0 m×4.0 m。类似的还有瑞典的Malmberget铁矿，其主要结构参数(H×B)也是经历了15.0 m×15.0 m→20.0 m×22.5 m→30.0 m×25.0 m的发展过程。可以说，(18～30 m)×(18～30 m)的大结构参数已经成为国外无底柱分段崩落法矿山的主流采场结构参数。

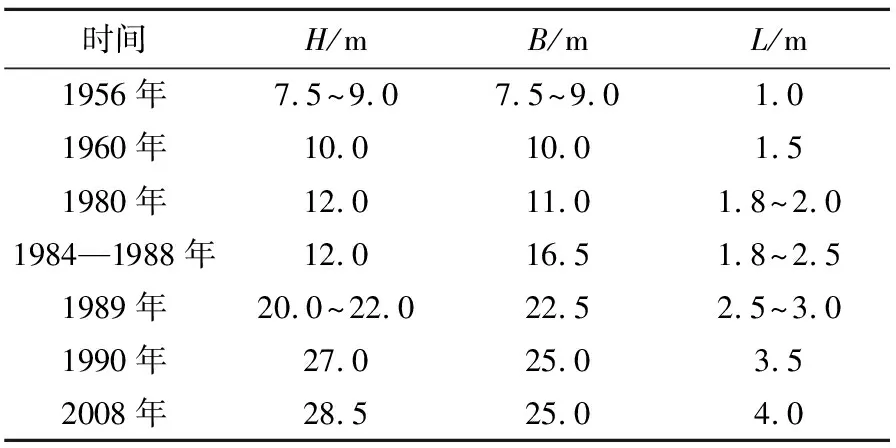
表1 瑞典Kiruna铁矿采场结构参数演变情况

我国无底柱分段崩落法采场结构参数的发展也大致经历了由小到大的过程，如：梅山铁矿自1965年建矿以来，其主要采场结构参数(H×B)经历了10 m×10 m→12 m×10 m→12 m×15 m→15 m×15 m→16 m×15 m→15 m×20 m→18 m×20 m的发展过程。表2统计了我国部分无底柱分段崩落法矿山的主要采场结构参数。由表2可以看出，目前我国大型无底柱分段崩落法矿山也已经发展到了(18～30 m)×(8～30 m)的大结构参数阶段，最具代表性的有：昆钢大红山铁矿采场结构参数为30 m×20 m，本钢大台沟铁矿采场结构参数为28.5 m×25.0 m。这些矿山的普遍特点是矿体厚大陡立、矿岩稳固，具备使用大结构参数的先天条件。而对于一些矿岩破碎或矿体倾角较缓、厚度不大的矿山，目前大多采用的是(12～15 m)×(12～15 m)的中等结构参数，这主要是考虑到在开采技术条件不佳时，采用大结构参数将会对贫损控制、凿岩爆破及采场稳定性等带来一系列困扰[7]。

表2 我国部分无底柱分段崩落法矿山采场结构参数

通过调查国内外无底柱分段崩落法矿山采场结构参数的演变历程可以看出，无底柱分段崩落法采场的主要结构参数经历了一个从20世纪60年代(8～12 m)×(8～12 m)的“小结构参数”到20世纪90年代(12～18 m)×(12～18 m)的“中结构参数”以及21世纪后的(18～30 m)×(18～30 m)的“大结构参数”的发展过程，且在发展过程中基本保持了分段高度大于进路间距的特点。

2 无底柱分段崩落法采场结构参数的确定方法

2.1 工程类比法

工程类比法是指一个新的工程在开始前参照已有类似工程的成功经验进行设计或施工的方法。工程类比法也是当前采矿工程领域的一种常用方法，主要用于采矿方法、采场结构参数、采矿工艺及参数以及支护方法和参数的确定等[8-10]。在采用工程类比法确定无底柱分段崩落法采场结构参数时，需要综合类比矿体产状、矿岩性质、产能规模、设备性能等因素。需要强调的是，对于一些开采技术条件较为复杂的无底柱分段崩落法矿山(如矿岩破碎，矿体厚度较小、倾角较缓、形态多变，地下水丰富等)，在利用工程类比法确定采场结构参数时，除了要考虑客观存在的不利开采条件外，还需要重点考虑自身应对复杂开采条件的施工技术水平及组织管理能力等。

2.2 理论计算法

1)基于典型椭球体相交理论的采场结构参数计算方法

在传统放矿椭球体(典型椭球体)研究中，认为无底柱分段崩落法单个回采单元的高度应为宽度的2.5～3.0倍，其根据是实测工业放出体的长轴尺寸为短轴尺寸的2.5～3.0倍，结合无底柱分段崩落法回采进路菱形布置原则，便可形成图3(a)所示的采场结构。由于分段高度与进路间距的比值约为1.3～1.5，因此在传统放矿椭球体研究中认为分段高度通常应大于进路间距。此外，由于无底柱分段崩落法崩落矿石具有转段回收的特点，传统椭球体理论认为要实现矿石的充分回收，就要使放矿椭球体相交，从而使放出体的形态尽可能地与“步距崩落矿石堆体+残留矿石堆体”的形态相符[见图3(b)]。

图3 根据椭球体相交理论确定采场结构参数方法示意图

由此，便可参照图3(b)所示的放矿椭球体排列关系并按照低贫化放矿可能形成的脊部残留形态来计算分段高度与进路间距的合理值，对于崩矿步距则可按照放出体厚度的1/4左右进行估算，具体计算公式[11]如下：

(1)

式中：H为分段高度，m；B为进路间距，m；L为崩矿步距，m；hd为进路高度，m；wd为进路宽度，m；θ为脊部残留体坡线角度，覆岩下出矿时取70°；a为放出椭球体长半轴；b为放出椭球体短半轴；ε为放出椭球体偏心率，ε2=1-b2/a2。

计算前需先确定合理的分段高度及进路尺寸，并通过物理实验测定放出椭球体的偏心率，随后将各参数代入式(1)便可算得合理的进路间距和崩矿步距。按照式(1)对不同放出椭球体偏心率下的采场结构参数进行了计算，结果见表3。

表3 根据放矿椭球体相交理论确定的采场结构参数

此外需要说明的是，目前业界对于放出椭球体的相交方式及相交程度尚未有统一的认识，放出体的相交状态因采场结构参数和放矿控制参数的不同而有所差别，图4展示了3种不同的放出体相交状态。相对而言，图4(c)所示的放出椭球体相交状态更接近实验观察得到的结果。显然，采用不同的放出体相交状态，最终计算出的采场结构参数也将有所不同。因此，不论采用哪种椭球体相交状态进行无底柱分段崩落法最佳采场结构参数的计算，都只能视为一种近似值。

图4 几种放出椭球体相交状态示意图

这种基于椭球体相交理论而提出的采场结构参数计算方法，其出发点在于使放出体形态与“崩落矿石堆体+残留矿石堆体”形态最大限度地保持一致，从而确保矿石的回收效果。

2)基于随机介质放矿理论的采场结构参数

计算方法

任凤玉[12]基于随机介质放矿理论，从进路出矿要充分回收步距崩落矿石及脊部残留矿石的角度出发，提出了一种确定合理进路间距的方法，认为合理的进路间距应使出矿时的有效流动带边界完整地包含步距崩落矿石及其上分段脊部残留体，同时又不与相邻脊部残留体相交[见图5(a)]，进而由该关系确定出合理进路间距的经验公式[见式(2)]。在采用该方法计算合理进路间距之前，需要先确定出合理的分段高度，同时通过端部漏口放矿达孔量实验，测出垂直进路方向的矿石散体流动参数。图5(b)为达孔量实验模型。

图5 任凤玉[12]提出的进路间距确定方法示意图及达孔量实验模型

(2)

式中，α、β为垂直进路方向的散体流动参数，μ与废石漏斗在进路顶板的出露宽度有关。当采用无贫化放矿方式时，μ≈0；当采用低贫化放矿方式时，μ≈0.1～0.6；当采用截止品位放矿方式时，μ≈0.75。

该方法从实现崩落矿石回收全覆盖的角度出发确定采场结构参数，目前已应用于北洺河铁矿[13]、小汪沟铁矿[14]、海南铁矿[15]等矿山的采场结构参数确定(或优化)中，并取得了较好的应用效果。

3)基于非典型椭球体理论的采场结构参数

计算方法

美国著名采矿专家KVAPIL[16]提出了一种基于非典型放矿椭球体理论的无底柱分段崩落法采场结构参数计算方法，该理论认为放出体并非标准的椭球体，而是一种类似“炮弹”形状的椭球体；该方法的基本原理是在确定采场结构参数时，使放出体最大限度地包含步距崩落体和上分段脊部残留体。

采用该方法确定采场最优结构参数时，应先确定出采场拟采取的进路尺寸和形状以及分段高度，再由分段高度估算出放出体高度(分段高度一般为放出体高度的2/3)，在此基础上利用非典型椭球体放矿理论对进路间距和崩矿步距进行计算，该方法的计算原理及主要参数含义如图6所示。

图6 KVAPIL提出的采场结构参数设计方法及参数含义

该方法的计算公式为

(3)

式中：WT为放出体(非典型椭球体)最大宽度，m；W′为理论放出体宽度，m；γ为有效出矿宽度，m；hT为放出体高度，m；dT为放出体纵向厚度，m。

在利用式(3)计算进路间距和崩矿步距时，先通过图7(a)所示的hT(包含进路高度)与W′的关系确定W′的取值，再根据图7(b)所示的γ与进路尺寸及形状关系确定γ，由此便可确定WT，进而计算出进路间距和崩矿步距。

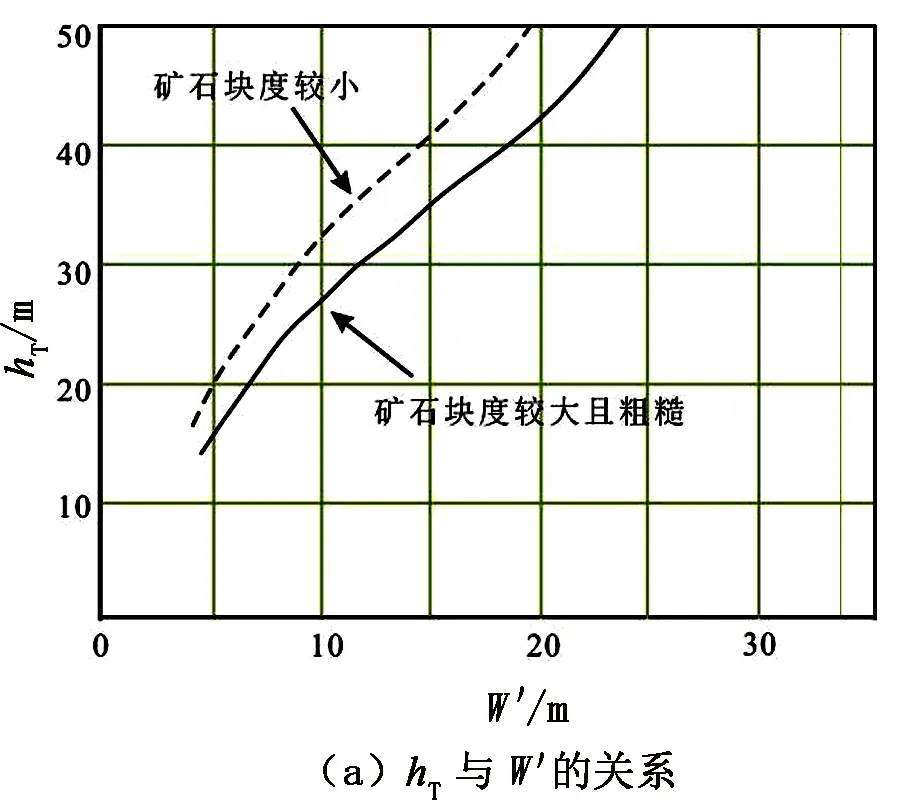
图7 理论放出体宽度及有效出矿宽度确定方法示意图

以某铁矿采用该方法确定采场结构参数为例进行计算演示。某铁矿已初步确定分段高度为20 m，进路宽4.5 m、高4 m，进路形状采用了利于矿石散体放出的直墙近平顶(r=wd/5)形式，矿山崩落的矿石块度较大且粗糙。根据以上信息，由分段高度以及图7(a)所示关系先确定hT约为30.0 m；再根据图7(a)确定W′为11.5 m；由图7(b)确定γ≈0.5wd，即为2.3 m；通过式(3)求出WT=12 m；根据B18 m时)，取B=18.0 m；L≤WT/4=3.0 m，取L=3.0 m。由此确定该矿山结构参数为20.0 m×18.0 m×3.0 m。

国外无底柱分段崩落法矿山常用此方法确定采场结构参数，由于其基本遵循了放出体形态与“崩落矿石堆体+残留矿石堆体”形态相一致的原则，因此在实际应用中取得了较好的矿石回收效果。

4)基于椭球体相切排列理论的采场结构参数计算方法

在我国无底柱分段崩落法发展过程中，曾出现了一种基于“椭球体相切排列理论”的无底柱分段崩落法采场结构参数设计和优化方法[17]。该理论认为传统放矿理论违背了纯矿石放出体应该相切的基本原则，进而研究了多个放出体相切的空间排列关系，认为采场结构参数优化的实质就是放出体空间排列的优化问题，密实度最大者为优。根据这一理论演化出了两种最优结构模式，一种为高分段结构，一种为大间距结构(见图8)，同时分别推导出了高分段和大间距采场结构参数计算公式。

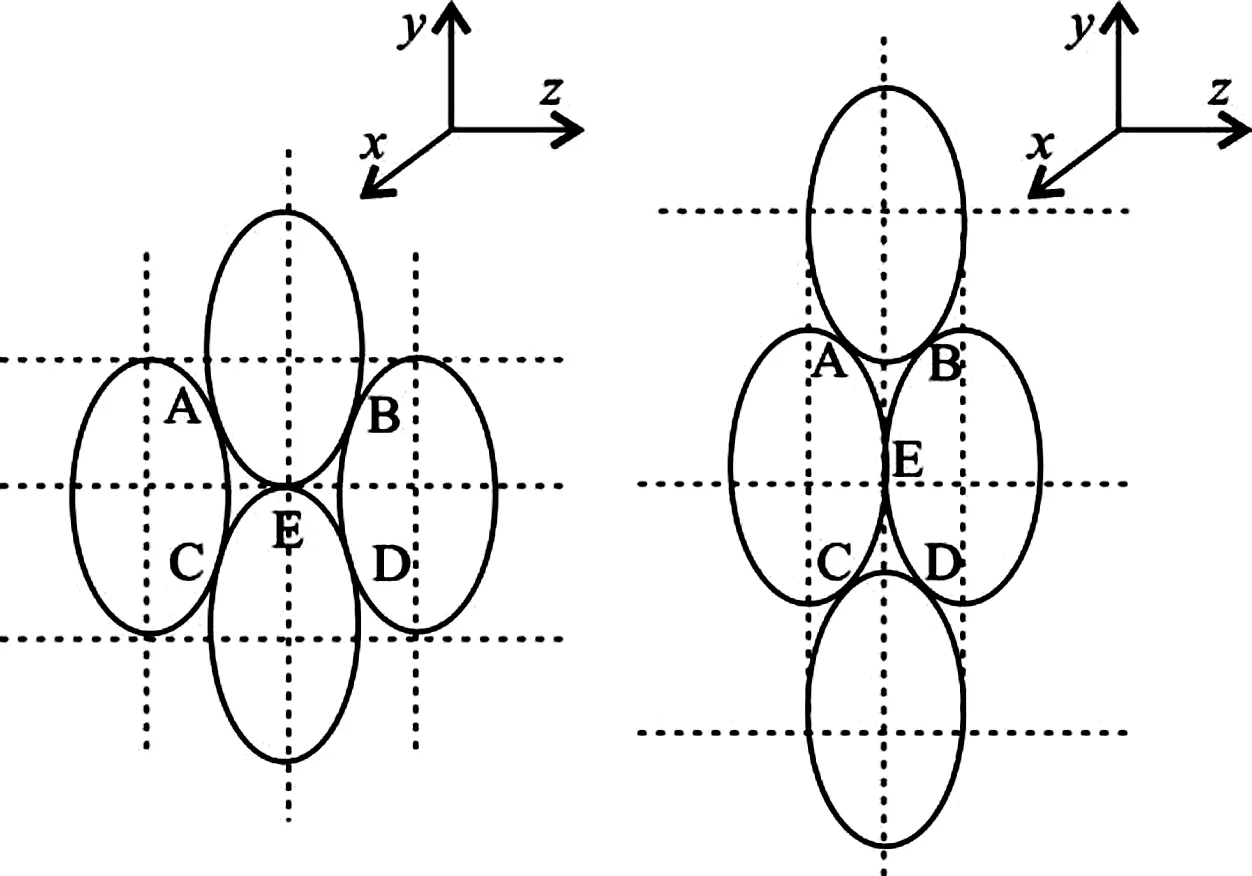
(a)大间距结构 (b)高分段结构

大间距结构参数的计算公式为

(4)

高分段结构参数的计算公式为

(5)

该理论的提出使我国无底柱分段崩落法曾在一段时间内呈现出了所谓的“大间距结构参数”和“高分段结构参数”两种形态和发展趋势[18-19]。然而，其应用和推广却不如人意，甚至已经被相关矿山摒弃，究其原因，主要是根据这种理论得到的结构参数未能在实际生产中取得理想的矿石回收效果。

图9是根据椭球体相切排列理论得出的大间距结构及高分段结构的放出体与实际矿石堆体(崩落矿石+矿石残留)的关系图。由图9可知，在大间距结构和高分段结构方案下，有相当大比例的残留矿石甚至部分崩落矿石处于放出椭球体之外，说明该理论实际上并未遵循“崩落矿石堆体+残留矿石堆体”与放出体形态保持一致的原则，这一点也已经被实验研究所证实[20]。如果放出体不能将崩落矿石以及残留矿石完全包括进去，说明这不是一个合理的结构参数方案，更不是最优结构参数方案。

图9 大间距及高分段结构方案的放出体与残留体关系

此外，按照高分段结构参数的计算公式分别计算了两种分段高度(15、18 m)在不同偏心率(ε)下的进路间距(见表4)。由表4可知，两种分段高度对应的进路间距仅为5～8 m，过小的进路间距极易引发采切工程量偏大和采场结构稳定性变差等问题，严重影响采矿生产及其经济效益，在实际生产中这样的结构参数几乎不具备应用价值，因此不能称其为最优结构参数方案。

表4 由高分段结构计算公式得出的进路间距

谭宝会等[20]的研究表明，根据椭球体相切排列理论确定采场结构参数是对无底柱分段崩落法放矿过程的一种错误认知，无底柱分段崩落法的放矿过程是一个动态过程，崩落矿石的形态、位置、块度等会随着放矿的进行而不断变化，因此实际放矿过程中各单元的放出体形态及大小在时间及空间上都是相互关联和相互影响的，且这种影响基本上是单向的(从分段上看是上影响下，从步距上看是前影响后)。放出椭球体的交叉是因为矿石的充分回收需要放出体交叉(即崩落矿石的转段或转步距回收)，放出体交叉是在不同时间上的空间位置交叉，交叉部分正是从其他位置转移至此且需要再次回收的残留矿石。放出体交叉并不意味着矿石的重复放出以及贫化的产生，而是崩落矿岩在采场内移动规律的准确体现[21-22]，也是矿石充分回收的必要技术措施。

综上所述，以上几种方法均是根据放出体与崩落矿石堆体及矿石残留体之间的契合关系来计算采场结构参数的，其根本目的都是希望放出体形态最大限度地与“崩落矿石堆体+残留矿石堆体”形态保持一致。但由于放出体的实际空间发育过程及其形态目前尚未完全探明，因此所计算出的最优采场结构参数均只能视为一种近似值。

2.3 物理实验方法

采用物理实验方法确定无底柱分段崩落法采场结构参数时，需要先按照一定的比例制作物理放矿模型，模型的比例尺一般为1∶100或1∶50，并按照现场崩落矿岩块度比例进行放矿散体颗粒配比。物理放矿实验的优势是可对采场结构参数进行仿真还原并开展放矿模拟，通过物理实验能够观察到一些在理论研究及现场实验中无法观察到的现象[23-24]，进而对各种结构参数下的矿岩移动规律和矿石回收指标进行分析研究，从而确定出理想的结构参数。

考虑到物理实验方法还具有占地少、成本低、实验结果可靠度高等一系列优点，该方法是目前确定无底柱分段崩落法结构参数时最常用的一种方法。如：高锋等[25]结合某铁矿实际开采条件，制作了比例尺为1∶50的立体放矿模型并进行了放矿实验研究，得出该矿最优崩矿步距为3.6 m，采用18 m的进路间距更有利于提高矿石回收率；刘文胜等[26]针对眼前山铁矿东部-213～-303 m矿体，制作了比例尺为1∶100的物理放矿模型并开展了放矿实验，得出最优采场结构参数为22.5 m×26.0 m×2.3 m；陈烈等[27]针对某矿实际开采条件，按照1∶100的比例制作了12 m×15 m×2 m以及15 m×15 m×2 m两组不同结构参数的物理放矿模型，并开展了放矿实验研究，结果表明，12 m×15 m×2 m的结构参数具有更优的矿石回收效果；行鹏飞等[28]以某铁矿为工程背景，通过物理放矿模拟实验研究了不同崩矿步距下矿石的贫损指标，得出当崩矿步距为3.7～4.2 m时，矿石贫损指标较好。

目前常用的放矿实验模型可以分为平面模型(单步距多进路多分段或单进路多步距)和立体模型(单分间立体模型或多分间立体模型)两类，前者主要用于观察放矿过程的一些物理现象，后者主要用于参数优化研究和矿石回收指标预测。相对而言，立体模型实验结果的准确率和可靠度要高于平面模型，但因立体模型实验工作量巨大，通常是在初步确定了结构参数之后，再利用立体模型研究该参数下的矿石回收指标。图10展示了西南科技大学采矿技术与矿山安全团队近年来制作的一些典型的物理放矿模型，利用这些模型开展放矿实验得出的研究成果可为矿山实际生产提供指导。

图10 西南科技大学制作的几组物理放矿模型

由于物理实验反映的是一种客观真实的放矿过程，这种方法在几何相似和物理相似等方面具有较好的仿真效果。但该方法在使用过程中也存在一些不足，主要体现在：①目前大多数研究仍采用精准度较低的平面模型，无法充分体现采场中各类残留矿石转段或转步距回收的过程；②当前物理模拟放矿难以做到与真实放矿在力学上的相似，尤其是难以实现覆岩压力、爆破冲击力以及地下水对矿岩散体力学性质的影响，后期应加强这方面的研究，使物理实验结果更加准确。

2.4 数值实验方法

近几十年来计算机硬件及软件技术飞速发展，计算机卓越的数值计算能力也被应用于工程问题的计算和求解之中，其中就包含了采用数值实验方法确定无底柱分段崩落法采场结构参数。采用数值实验方法研究无底柱分段崩落法采场结构参数，主要是从矿石回收效果以及采场稳定性两方面入手，前者大多采用离散元软件进行模拟，后者主要采用有限元软件进行模拟。

早在20世纪60年代，加拿大的JOLLEY就已提出采用九块随机递补模型来进行放矿仿真计算的方法，该方法主要是从块体随机移动概率的角度模拟放矿过程，其原理见图11(a)。在随后的几十年里，学者们又在随机介质放矿理论的基础上，从移动场相似的角度出发，用散体移动概率密度方程反求模块递补概率值，从而提高了这种模拟方法的可靠性[29]。但该方法考虑更多的是块体的随机移动概率，而忽略了放矿过程中矿岩散体力学性质对放矿过程的影响。

近年来，各类力学计算软件相继出现，使得岩体力学行为模拟的仿真度大幅提升，所获得的模拟结果也更接近真实情况，其中最具代表性的是ITASCA公司研发的颗粒流离散单元法软件(Particle Flow Code，PFC)和有限差分法软件(Fast Lagrangian Analysis Code，FLAC)，图11(b)展示了采用PFC3D软件模拟得到的无底柱分段崩落法端部出矿放出体形态。

图11 数值模拟放矿效果示意图

目前这些数值计算软件已被广泛应用于模拟放矿过程和确定无底柱分段崩落法采场结构参数，如：赵颖龙等[30]基于大间距结构参数理论，采用PFC3D软件对某矿进行了模拟研究，得出该矿采用30.0 m×25.0 m×5.5 m的结构参数可获得较优的矿石回收效果；舒平[31]结合某铁矿矿体赋存状况及生产条件，运用PFC3D软件对9组结构参数进行了放矿模拟，得出该矿最优采场结构参数为14 m×16 m×3 m；丁航行等[32]针对梅山铁矿18 m×20 m的采场结构参数，采用PFC3D软件对6组崩矿步距方案进行了放矿模拟，得出最优的崩矿步距为2.2 m。此外，郭辉文等[33]从采场稳定性的角度出发，采用有限元软件FLAC3D分析了龙首矿西二采区无底柱分段崩落法采场分别取12 m×15 m和15 m×15 m两种结构参数时的采场稳定性问题，结果表明，采用15 m×15 m的结构参数可使采场具有更好的稳定性。

总体而言，数值实验方法具有成本低、应用灵活、计算效率高等优点，而且能进行大量不同参数方案和大范围放矿案例的实验研究，因此该方法是未来最具潜力的一种研究手段。但是，当前研究中也存在一些不够完善之处，如：建立的数值模型往往在边界条件、力学参数设定等方面与实际情况存在较大偏差；数值实验过程和计算结果很容易受人为因素控制，模拟结果的可信度有待进一步提升。此外，实现多场耦合的散体放矿数值计算(如考虑渗水状态下的放矿过程)以及覆岩压力和构造应力条件下的放矿模拟也是未来该领域的重点研究方向之一。

2.5 现场实验方法

现场实验方法主要是通过在矿山实地测定放出体形态，将放出体形态与崩落矿体(包括残留体)的形态进行对比，从而掌握结构参数与矿石回收效果之间的关系。目前测定放出体形态的主要手段是标志物回收法，即提前在炮排崩落范围内按照一定的规则埋放一系列标志物，然后在放矿过程中对这些标志物进行回收，根据所回收的标志物原始空间位置及对应的放出矿量，便可绘制出实际的放出体形态。

早在1971年，瑞典的Timmergruvan铁矿就通过在中深孔炮排崩矿范围内安置标志物的方法测定了实际放出体的形态，图12(a)展示了该矿山现场实测的放出体形态。从图12(a)中可以看出，现场实测的放出体并非标准的椭球体，而是一种不规则的类椭球体。澳大利亚的Ridgeway金矿在2002-2005年也进行了放出体形态的现场测定实验，结果表明，相对于放矿方式和地质参数，中深孔的爆破参数对于矿石的回收效果有更为显著的影响[34]。

近年来，我国的梅山铁矿[35]采用安置标志物的方法对矿山18.0 m×20.0 m×2.6 m结构参数下的放出体进行了测试，得到的放出体形态见图12(b)，研究结果表明，在该结构参数下，进路间距与分段高度之比偏大，导致矿石回收效果不理想，继而提出将采场结构参数优化为22.0 m×20.0 m×2.4 m，并开展了现场工业试验，最终使采场矿石回采率由85.47%提升至90.64%，贫化率由11.52%降至9.95%。

图12 矿山实测的放出体形态

现场实验方法能否成功的关键在于标志物是否能被最大限度地识别并回收，标志物回收得越充分，所能获取的信息就越多，最终据此得到的放出体形态也就越精准。鉴于此，在制作标志物时应遵循3个基本要求：①要便于安装，且要保证在爆破和放矿过程中不被破坏；②应具有与散体矿岩类似的流动性，能够随着放矿的进行被放出；③要便于识别和筛分。

Ridgeway金矿所采用的标志物是由外径42 mm、壁厚4 mm的橙色空心钢管制成，长度为250 mm，为了使标志物的密度尽可能接近矿岩密度，在管中填满了水泥，同时在钢管外壁焊刻4个字母作为每个标志物唯一的身份识别代码[见图13(a)]。最后在出矿过程中通过磁性分离以及人工肉眼识别相结合的手段来筛选和回收这些标志物，该标志物的优点是成本低廉，缺点是当标志物埋入矿堆较深时，很难被识别和筛分出来。

为了提高标志物的识别效率和识别性能，梅山铁矿[36]在现场放出体测定试验中制作了一种基于无线射频识别技术(Radio Frequency Identification，RFID)的标志物[见图13(b)]，该标志物是将RFID电子标签连带供电电池一并封装在特制的防爆PP-R空心管材中(其外径为50 mm、内径40 mm、长度200 mm)，每一个标志物都具有唯一的电子标签编码，同时在爆堆附近及溜井附近巷道壁上安装RFID电子标签阅读器及摄像头，以识别被放出的标志物。经测试，这种标志物在矿堆中的埋深为0.1～0.5 m时能够被有效识别，但当其埋深超过1 m时便难以识别。

图13 用于现场测定放出体形态的标志物

综合来看，现场实验方法具有数据真实、可靠等优点，其结果对于采场结构参数的优化也更具指导性，但这种方法工程量较大，尤其是标志物的安装和筛分过程复杂且费时、费力，成本较高。这种方法还需对以下几个方面展开研究：①继续研发高识别性能的标志物或识别技术，从而进一步提升标志物的识别效率和精准度；②进行多分段的标志物回收实验，即观察未能在本分段回收的标志物，是否会以残留矿石的方式在下分段得到回收，以及出矿至何种程度才会被回收；③研发可以记录移动轨迹的标志物，从而掌握标志物在矿堆中的位移迹线。此外，进一步研发更为简便高效的现场放出体测定技术或方法也是需要重点考虑的方向之一。

3 无底柱分段崩落法采场结构参数确定原则

在确定无底柱分段崩落法采场结构参数时，应系统地考虑分段高度、进路间距以及崩矿步距这3个参数之间的匹配关系。在无底柱分段崩落法采场结构参数中，分段高度的确定相对独立和简单，因此可以率先确定，继而根据放出体形态与“崩落矿石堆体+脊部残留体”形态应保持一致的原则确定进路间距。当分段高度和进路间距确定之后，便可确定崩矿步距，相对于分段高度和进路间距，崩矿步距的调整对生产影响最小，因而易于优化。最终，这3个主要参数理想的匹配关系是，可以使放出体形态与“崩落体形态+各种残留体”形态无论是在垂向上还是在纵向上(即沿进路方向)均能够最大限度地吻合，从而实现矿石的充分、低贫化回收。

3.1 分段高度的确定原则

一般来说，分段高度越大，采准系数就越小，一次崩落的矿量也就越多，生产强度随之增大，而采矿成本则随之降低。但是分段高度的选取受制于凿岩设备的能力，即合理的分段高度必须在凿岩设备的能力范围内。近年来，随着凿岩设备的不断更新，尤其是凿岩深度更大和精度更佳的液压凿岩台车的出现，为无底柱分段崩落法矿山分段高度的提升创造了更大的可能性，如：大红山铁矿引进SimbaH1354液压凿岩台车后，分段高度由20 m提升至30 m；酒钢镜铁山铁矿在引入SimbaH-252液压凿岩台车后，分段高度由15 m提升至20 m。

尽管液压凿岩台车的出现提升了分段高度，但液压凿岩台车存在一个最佳凿岩深度范围，在该范围内凿岩效率和精度都较高，凿岩深度一旦超出该范围，则效率和精度都将降低。对于无底柱分段崩落法的扇形炮排来说，中心孔的深度最长，一般可达到分段高度的1.5～1.8倍，即其长度随着分段高度的增加而成倍增加，一旦炮孔的深度超过设备的最佳凿岩深度时，凿岩效率和精度将大幅下降，可能引发频繁的悬顶、隔墙、大块等问题。同时，目前国内大部分矿山依旧采用的是人工把管的风动装药器(如BQF-100型风动装药器)，若炮孔过深，不仅装药强度大，且装药质量也无法保证。此外，当矿岩较为破碎时，炮孔深度越大，炮孔发生变形、堵孔、错孔的概率也就越大，不仅增加了后期疏孔和补孔的工作量，还很容易影响装药和爆破质量。因此，合理的分段高度应该与矿岩性质、凿岩设备和装药设备能力等相匹配。

无底柱分段崩落法具有特殊的菱形采场结构，使得分段矿石具有转段回收的特点，实验表明，无底柱分段崩落法单分段的矿石回收率仅为30%左右，两个分段的矿石回收率可达60%，分段数目越多，矿石回收效果越佳[37]。所以在确定分段高度时还需要考虑矿体的垂向回采空间，通常在沿矿体延深方向上布置的分段数目不得少于3个，以保证矿石回收率。因此在确定合理的分段高度时，需要综合考虑采场产能、设备能力、矿岩性质、矿体规模等因素。

3.2 进路间距的确定原则

当合理的分段高度确定后，就可据此确定进路间距，既可通过工程类比法来确定进路间距，也可以通过式(1)-式(3)来计算合理的进路间距。除此之外，在确定进路间距时还需充分考虑矿山的地压管理需求，一般来说，大间距有利于降低应力集中、提高进路稳定性以及减少采准工作量。因此，若矿体稳固性较差、地压大，则进路间距可适当取大值，反之则取小值。如：龙首矿西二采区在确定无底柱分段崩落法采场进路间距时，采用式(2)计算出合理的进路间距为12.84～15.14 m；但考虑到西二采区矿岩松软破碎，为减小应力集中和采动地压对回采进路稳定性的影响，最终取15 m作为设计进路间距[38]。

3.3 崩矿步距的确定原则

根据随机介质放矿理论[12]可知，放矿时采场内每一个颗粒的迹线在出矿口都有相应的位置，因而通过在出矿口观察废石最先出露的位置，便可判别废石来自哪个方向。当崩矿步距过小时，正面废石会最先出露，废石漏斗在到达出矿口时与进路顶板眉线相隔一段距离，四周矿石流将废石流包围，即出现俗称的“包馅”现象，此时矿岩界面移动过程如图14(a)所示；而当崩矿步距过大时，则表现为顶部废石最先流到出矿口，此时顶部废石在出矿口眉线部位呈薄层流出，由于流轴偏离端壁一段距离，加之在端壁上方的靠壁残留矿石投入移动，使顶面废石到达出矿口时不紧贴出矿口眉线，而是隔着一层很薄的矿石层，废石混杂矿石流出，但此时废石流出速度较慢，废石在端部口出露的部位较高[见图14(b)]。合理的崩矿步距应是正面废石和顶部废石同时达到出矿口，而且废石出露的时间较晚，一旦出露则以较快的速度流出，从而在出矿口占据较大的断面，此时放矿作业很快会达到截止品位。

图14 不同崩矿步距下矿岩接触面移动过程

在实际生产中，很难一次性将崩矿步距确定至最佳值，通常是先初选一个崩矿步距，再根据实际生产数据对其逐步优化。初选崩矿步距时，应综合考虑崩落矿量、爆破效果、矿石回收效果、眉线保护等因素，运用工程类比法或理论计算法选定初始值。根据初选值设计1～2个分段的中深孔爆破参数，待覆盖层形成后在正常回采条件下，按上述方法观察进路端部废石的出露信息，再对崩矿步距进行动态优化，直至获得最满意的回采效果，此后便可按照最佳崩矿步距进行后续分段的设计和施工。

4 最优采场结构参数探讨

4.1 当前常用结构参数确定方法的不足

分析上述常用的无底柱分段崩落法采场结构参数确定方法可以看出，当前的采场结构参数确定(或优化)方法基本上都是以能否实现最优的矿石回收指标为出发点，甚至是将矿石回收指标作为评判最优采场结构参数的唯一标准。然而事实是，采场结构参数不仅会影响矿石的回收指标，同时也关联到采切工程量、采场产能、采矿效率、采矿安全性等多个采矿技术经济指标，单一的矿石回收指标最佳并不能说明整个矿山的技术经济指标也处于最佳状态。因此，无底柱分段崩落法采场结构参数的寻优绝不单单是寻找可获得最优矿石回收指标的结构参数，而是寻求一个可使整个无底柱分段崩落法采矿系统处于最优技术经济指标的结构参数。

4.2 频繁调整采场结构参数带来的问题

当前有一部分矿山频繁对其采场结构参数进行调整以寻求理想中的“最优”参数，而事实上，当一个无底柱分段崩落法矿山的采场结构参数(主要是分段高度和进路间距)确定后，在非必要情况下切勿频繁对其进行更改，这是因为结构参数的调整会对矿山的开拓、运输、采准与切割、装药爆破以及设备适应性等方面产生巨大影响，尤其是进路间距的改变，更是破坏了上下分段回采进路菱形交错布置的基本结构，势必严重影响矿山的生产管理和矿石回收效果。因此，采场结构参数的调整必须非常慎重且不能过于频繁。

4.3 采场结构参数过大可能带来的问题

目前国内外无底柱分段崩落法矿山的采场结构参数均有不断增大的趋势，尽管采场结构参数的加大在降低采准系数、提高产能和采矿效率等方面起到了正面作用，但并非越大越好，必须意识到过度加大采场结构参数可能造成的负面影响。其实，早在2008年著名采矿学者W.Hustrulid和R.Kvapil[31]就已提出当时的无底柱分段崩落法采场结构参数已经过大(主要指分段高度和进路间距均大于25 m)，过大的采场结构参数给矿石回收以及矿山管理带来了不利影响，主要体现在切割拉槽难度增大、炮孔维护难度增大、装药难度增大、大块率提高、悬顶事故频率增加以及出矿管理难度加大等方面；而这些现象在我国矿山也已出现，如大红山铁矿在将分段高度增大至30 m后，炮孔的变形和堵孔现象随之发生，导致矿山悬顶事故频率明显增加[39]。

综上所述，对于无底柱分段崩落法矿山而言，并没有绝对最优的采场结构参数，在确定采场结构参数时不能单以矿石回收指标最佳作为唯一的评判标准，而要综合考虑矿体产状、矿岩力学性质、矿山规模、设备能力以及技术管理水平等诸多因素，采场结构参数一旦确定，在非必要情况下切勿频繁对其进行调整；同时需要注意的是，矿山在追求大结构参数所带来的经济效益时，也必须充分考虑如何消除结构参数过大可能带来的一系列负面影响。

5 结论

a.随着采矿技术、放矿理论以及配套采矿设备的迅速发展，无底柱分段崩落法采场的主要结构参数已从最初的(8～12 m)×(8～12 m)的“小结构参数”发展至目前的(18～30 m)×(18～30 m)的“大结构参数”，而且在发展过程中基本保持着分段高度大于进路间距的原则。

b.目前确定无底柱分段崩落法采场结构参数的方法主要有工程类比、理论计算、物理实验、数值实验以及现场实验等方法，各方法有其优缺点及适用环境，但无论采用何种方法，只有遵循了放出体形态与“崩落矿石堆体+残留矿石堆体”形态一致的原则才能获得良好的矿石回收效果。

c.在确定无底柱分段崩落法采场结构参数时，应从整个采矿系统的技术经济指标最优的角度出发，同时应尽量避免频繁调整采场结构参数和盲目追求大结构参数。