基于IGWO-SVM的轴承故障诊断①
蒯升元
(安徽理工大学电气与信息工程学院,安徽 淮南 232001)
1 SSA-VMD 能量熵的特征提取
1.1 变分模态分解
VMD能自己选择出每一种状态的最好的中心频率和宽带,还能分解一些固定的模态分量。他的主要原则就是构造和解决变分问题。下面介绍VMD把故障信号分解成K个分量的模型:
(1)
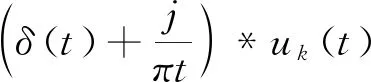
L({uk},{ωk},λ)=
(2)
通过公式2将最小化的问题变成了Lagrange的鞍点问题。
VMD的操作步骤:
(1)先把{uk},{ωk},λ初始化,然后选择模态个数和惩罚参数。
(2)对上面三个数进行迭代计算。
(3)
(3)观察是否满足终止条件,
(4)
其中式(4)中的ε是判断的精度,要是不满足终止条件,就返回到第②步继续,否则就直接输出模态分量。
1.2 SSA优化VMD
在VMD的分解当中,需要寻找合适的模态个数和相应的惩罚参数,K值选择不恰当的话,可能会出现分解过多或者是欠分解状况,惩罚参数选择不当可能导致信息丢失或者信息冗余情况。所以要确定最优的参数组合。这次利用麻雀搜索算法优化VMD中的参数,通过包络熵的极小值来寻优,包络熵是用来表示电机信号的稀疏程度,当IMF分量中噪声很多,关键特征信号少的时候,包络熵的值就会比较大,否则,包络熵值会比较小。
采用麻雀搜索算法是模范麻雀捕食的整个过程,假定存在一个D维的搜索空间,空间中有N只麻雀在觅食,那么在这个D维空间中,第i只麻雀的位置则表示为 :Xi=[Xi1,…,Xid,…,XiD](i=1,2,…,N),Xid表示第i只麻雀在第d维的位置信息[8]。 探索者一般占总群数量的10%~20%,则每次迭代过程中,探索者的位置更新公式为:
(5)
式中,t代表迭代次数;T代表最大迭代次数;α为(0,1]中的均匀随机数;Q为一个标准正态分布随机数;L表示一个1*d的矩阵,该矩阵内每个元素都为1;R2和ST(ST∈[0.5,1])分别表示预警值和安全值,当R2 追随者的位置更新公式如下: (6) (7) 其中优化的结果是K为麻雀个体的位置,麻雀的个体适应度值就是局部包络的极小值。 VMD在进行SSA的参数寻优后对电机的故障信号进行分解,会得到K个模态分量。然后对每个IMF分量进行FFT变换,通过计算每个IMF的能量熵来表示每个分量的分布情况。并且将这些IMF能量熵[H1,H2,…,Hn]作为特征向量。它可以表现出能量的分布情况和频率的复杂化,我们通常把能量熵定义为: (8) 式子中的n表示模态的个数,Ei是模态分量的能量,Pi是归一化后的能量。 灰狼算法是一种根据狼群捕食过程中的行为来发掘的一个新的优化方法,他有着收敛性好,涉及到的参数也比较少,比较容易实现,所以也采取它来优化支持向量机的识别。 即使灰狼算法相对于其他寻优方法有着较为明显的优势,但是灰狼算法本身却存在需要改进的地方,灰狼优化算法对高维数据寻优时,容易陷入局部最优和全局搜索问题。这是所有的群体智能算法在收敛过程都不可能是线性的,鉴于此,提出一种非线性的递降方法,迭代方法如下: (9) 上式中Tmax代表总的迭代次数,随着迭代次数增加,迭代速度减慢,实现了全局搜索,改进的收敛方式平衡了全局搜索和局部最优的问题,加强了算法全局的寻优能力,这种收敛方式更加贴近实际。 为验证提出的基于 SSA-VMD 能量熵特征提取和改进GWO-SVM 故障识别方法的有效性,采用美国凯斯西储大学轴承数据(CWRU)进行仿真实验,此数据对全球学者开放,数据特征明显,常用于轴承数据研究。实验平台由电动机、扭矩传感器、功率测试计、电子控制器组成,故障设置采用电火花单点损伤,使用加速度传感器采集振动加速度信号,采样频率分为12 kHz和48 k Hz。 下面主要使用VMD来将故障的原始信号进行处理,由于篇幅的有限,这里我们主要分析了电机轴承滚动体故障的信号分解和提取熵能量,其他的各种故障一样这样分析。 由下图可知各 IMF 中心频率相互独立,能够有效避免模态混叠问题,且VMD与递归式模态分解不同,即没有采用极值包络线递归方式求取IMF,边界效应问题远弱于递归式模态分解,采用该方法能够得到较单纯模态分量。 当发生故障时,不同的模态分量会含有不同的冲击成分。为查看每个模态分量含有故障信息情况,计算每个IMF分量的包络熵,经过一定的包络值筛选,分别计算其模态分量的能量熵并组成特征向量,用作故障诊断的输入数据。 采用 SSA-VMD 提取轴承数据特征,如下表所示,正常数据、内圈、外圈、滚动体等故障数据的特征向量为[H1,H2,H3,H4],对应标签分别为 1、2、3、4,各 100 个样本,共 400 个样本。 搭建IGWO-SVM算法模型是通过使用MATLAB编程语言。在通过谐波小波包来提取4种状态的样本480组,再将这些样本分成俩部分即训练集和测试集。训练集即是从这些样本中随机抽出400组,测试集即为剩余80组。通过训练集的输入,为了得到全局最优值来进行再训练,这是我选择了通过 AFSA对惩罚因子和核函数寻优,最后把得到的全局最优值分别赋给SVM的参数(C,σ)再进行训练。然后使用优化好的SVM分类器对剩余的80组测试集进行分类诊断,结果如图所示。 通过上图的对比可以知道原始的SVM表现最差,诊断分类出现了很多不准确的情况。然后相比较而言AFSA体现出的准确率最高,通过GWO和PSO处理后的SVM分类效果比较好。 在上述条件相同的情况下,对表1的数据进行分析能很好的看出来,IGWO-SVM算法模型识别出了79组,准确率高达98.75%,通过这一方法不仅一定程度上提高准确率并且用时也变短了。综上分析,IGWO-SVM 算法模型在故障诊断上有很好的效果,并且拥有准确率和效率更高的优势。 表1 采取的各个故障的特征向量 为了提高电机故障诊断分类判别的准确率,提出了使用IGWO来优化SVM的算法。首先,在特征向量的提取上应用改进后的谐波小波包分解对原始的谐波信号进行分解重构来得到,接着为了得到SVM的最优参数(C,σ),需要对SVM模型中的参数进行自适应的优化,采用了IGWO算法来完成的。通过这一分类技术对轴承的故障类别来进行分类判别,大大提高了故障诊断的准确率。 与此同时还缩短了诊断的用时。通过对比IGWO优化后的SVM算法模型和原始SVM和PSO优化的SVM三者,对比发现提出的方法在故障诊断方面具有更好的效果。由此可见此优化模型具有很好的实际应用价值。未来可推广应用于其他领域的故障诊断。1.3 特征值的提取
2 基于IGWO-SVM 的分类模型构建
2.1 灰狼算法
2.2 改进灰狼优化算法
3 实验仿真模型
4 IGWO-SVM故障诊断

5 结 论

