轮腿式变胞机器人变形结构设计及其动力学分析①

刘红艳

(安徽文达信息工程学院，安徽 ？230000)

0 引 言

机器人被人们广泛应用于高危救险、工业制造以及医疗等领域。机器人类型多样，功能各不相同，能够代替人类从事很多工作内容。特别是小型移动机器人成为目前各国主要研究的对象，小型移动机器人具有良好的隐蔽性，在复杂、多变的环境中能够完成机器侦查、跟踪等特殊任务[1]。目前小型移动机器人运动形式主要有轮式与仿真足两种，轮式结构运用场景多样、适应性强，同时灵活性、效率都更高[1-2]。不过轮式机器人在结构化复杂的场景面临移动困难问题，因此针对小型化轮腿式移动机器人展开研究，分析机器人运动力学参数，优化轮腿式机器人在复杂环境下的运动效果，为相关性移动机器人提供理论技术参考。

1 轮腿式变胞机器人变形结构设计

轮腿式机构在机器人运动中的优势明显，特别是传统障碍物圆轮结构难以跨越，而可变轮腿式可以以腿式进行障碍物的跨越。变形轮的设计中，要使得轮、腿模式实现灵活的变化，提升结构运动效率，就需要对机构组间进行参数优化，如车轮变化状态产生的力矩越小，其转换成的运动效率就越高，同时机器人可以越过的障碍物将由变形轮变形前后的直径比而定[4-5]。所以在设计优化中主要优化驱动力矩以及两种模式下的半径比，变形轮变化状态如图1所示。

如图1(a)所示，变形轮两组四连杆结构保持稳定，其中ACCD均为腿i上四个点参数，变形轮三条腿等效，且运动相同，运动拓扑结构始终保持旋转中心对称。其中圆轮半径为R，轮辐半径为lOA，可以到变形轮设计变量如式子(1)所示。

(1)

变形轮变化由四连杆结构改变产生，如图1(b)所示得到机构约束关系如式子(2)所示。

(2)

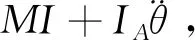
(3)

式子(3)中m为构建腿3外构架总质量。变形轮变经比为λ，根据变形几何关系得到等效半径lOD3表达式(4)。

(4)

结合变形轮几何推导公式得到lB3D3以及变量cosδ，结合式子(4)得到变径比与lOA之间的函数关系。

对变形轮的约束中，确定圆轮半径R，圆轮轮辐半径lOA不能随意取值，因此可以得到几何约束表达式如式子(5)所见。

(5)

变形轮机器稳定性的研究采取稳定锥方法求解机器人整机模型，通过判别关系来判别机器人是否有倾翻问题，具体如图2所示[7]。

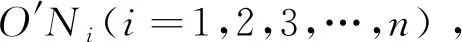
在机器人斜面稳定性研究中，机器人要具备稳定的条件是凸边形与机器人稳定锥之间的边和夹角的夹角应该大于0。由质心O′为原点建立坐标系，三个角点到O′可以表达为式子(6)。

qi=(qix,qiy,qiz)t(i=1,2,3)

(6)

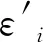
(7)

机器人稳定角可以表示为式子(8)。

(8)

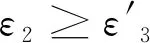
2 机器人运动控制平台仿真测试

由图3可知，在机器人仿真测试中，初始位姿即便直线距离大于4米的情况下，所采用的控制方案机器人仍旧可以获得比较好的稳定控制效果，并且在10秒的时间内很快的获得跟踪参考位置。机器人调整速度与初始位姿误差、加速度约束以及运动速度约束有关，并且在实际测试中，机器人稳定调整效果也与增益常数的整定有关。

由图4仿真测试结果可以看出，在随时间变化的目标位姿运动曲线中，机器人所设计的位姿稳定控制方案可以在20s时间内获得参考位姿的跟踪，同时在测试结果中也可以看出机器人的实际速度与方向角都可以很快达到目标收敛值。采用带卡尔曼滤波九轴陀螺仪与高精度曲线功率计，对机器人两种运动模式做平面性能实验，如图5。

其中机器人的驱动输入转速ω，在实验测试中可以明显看出，机器人在圆轮模式下的运动效率是明显高于轮腿模式的。在外界条件以及初始参数一致状态下，变形轮机器人在不同的模式下的俯仰角相轨迹图，如图6所示。

从图6可以看出，圆轮模式中点(φ0,0)固有俯仰角为(φ0=10.08°;φ0=11.5°)，在测试中，机器人运动面并不理性，可能机器人制造工艺问题使得机器人的质心出现偏移问题，同时轮子运动中各个连接缝隙因素，圆轮模式实际相轨迹并并没有与(φ0,0)重合，不过在轮腿模式中极限环未重叠，并且机器人整体运动趋势正确。另外，通过对极限环半径的观察，相同运动条件下，圆轮模式俯仰角远低于轮腿模式俯仰角，说明机器人在圆轮模式下具备更出色的稳定性；最后进行1s内两种状态主动模式位姿变化，成功率100%。说明设计的机器人具备良好的稳定性与运动性能。

3 结 语

随着科学技术不断的发展与进步，机器人已经成为人们生活中不可或缺的帮手，小型化移动机器人在复杂非结构环境存在着效率、速度无法平衡的矛盾。因此设计一种新型的轮腿式移动机器人，基于变形轮方案提出一种主/被动结合变形轮方案，并设计出三幅轮腿式移动机器人；根据机器人变形轮设计特点，提出一种双轮差速对称整机布置方案，并对机器人稳定性进行优化；基于Matlab Simulink完成对机器人运动模型的搭建，仿真测试证明所设计的位姿稳定控制器具有良好的性能与稳定性；在机器人两种运动模式实验中，相同驱动环境下，证明轮腿模式速度更好，不过稳定性偏弱，在两种模式主动状态1s切换均可以实现100%功功率。不过本次研究也存在不足，所设计的机器被动状态稳定较差，后续研究可以增加对两轮同相位检测与控制研究，提升系统整体稳定。