基于M-K检验和最小二乘法的SSA算法研究①
贾国庆, 程明龙,*, 易辉跃, 房卫东, 许 晖
(1.青海民族大学物理与电子信息工程学院,青海 西宁 810007;2.中国科学院上海微系统与信息技术研究所,上海 201899;3.上海无线通信研究中心,上海 201210)
0 引 言
通过振动信号获取结构体的固有频率是监测结构体的工作状态及健康状况常用的方式。在振动信号的采集过程中,会夹杂一些直流分量和噪声,对分析结果产生影响;同时,传感器温度造成的零点漂移会产生线性趋势项,使信号严重失真[1-2]。如何消除不利影响因素一直是振动信号处理中的研究重点。文献[3]结合自适应噪声完全集合经验模态分解和奇异谱分析,对含噪信号进行自适应分解,然后使用SSA对信号层进一步降低低频噪声,能够较好地消除噪声的干扰。文献[4]提出一种基于相位空间重构和奇异谱分析的降噪法,通过奇异值分解对比噪声信号和有用信号的奇异值数目进行自适应降噪,重构原始数据。文献[5]介绍了一种滑动窗长SSA算法,通过改变轨迹矩阵的窗长,突破了特征分解的局限性,更利于提取真实信号。上述算法对信号突变严重的情况下有一定的优势,但是相位移动和奇异值突变的现象没有得到改进。针对上述算法的不足,提出了优化算法,通过对信号添加伪序列,并融合曼-肯德尔(Mann—Kendall, M-K)检验法和最小二乘法,可以避免信号相移的出现,降低突变奇异值的能量,自适应的选择分组重构阶次,从而增加SSA的降噪能力。仿真结果表明,改进SSA算法可以达到更好的降噪效果,提高了信号的信噪比,从而有效提取速度、位移和固有频率等信息。
1 奇异谱分析
奇异谱分析是研究非线性时间序列的高效方式,通过构建轨迹矩阵、SVD分解、分组和重构,可以获得原时间序列的趋势信号、周期信号和噪声信号,进而对序列进行分析,以去除噪声信号。
1.1 轨迹矩阵
存在有限长度的一维时间序列[x1,x1,…,xN],其中N为序列长度。选择一个合适的窗口长度L,将原始一维时间序列进行滞后排列,得到轨迹矩阵[6]:
(1)
窗口长度L通常小于N/2。令K=N-L+1,则轨迹矩阵X为:
(2)
1.2 奇异值分解
特征值的分解可以获取特征值与特征向量,以此分离振动信号的趋势项和周期项。在SSA中,使用SVD方式对轨迹矩阵进行奇异值分解式(3):
X=UΣVT
(3)
式(3)中,U为左奇异值矩阵;Σ为对角矩阵,即奇异值;V为右奇异值矩阵。U和V均为单位正交矩阵[7],满足UUT=I,VVT=I,令
S=XXT
(4)
对S进行奇异值分解,得到对应奇异值λ和奇异值向量U=[U1,U2,…,UL]。对λ进行降序排列:λ1>λ2>…>λr≫λr+1>…λL≥0,第r个奇异值远大于第r+1个奇异值,说明在第r个奇异值之后的奇异值即为噪声信号。可以根据重新排序后的奇异值的能量占比情况,选择含有有效信号的前r个奇异值向量。
对于实际信号序列有式(5):
(5)
式(5)中,为确保窗口长度小于N/2,d=min{L,K}。所以,轨迹矩阵X的SVD分解结果为式(6):
X=X1+X2+…+Xd
(6)
1.3 分组和重构
将式(6)的下标d划分为m个互不相交的子集I1,I2,…,Im,令I={i1,i2,…,ip},则对应I的矩阵XI=Xi1+Xi2+…+Xip。因此可得式(7):
X=XI1+XI2+…+XIm,(1≤m≤L)
(7)
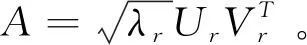
为了得到分解后的序列,这里将式(7)中的每个矩阵XIj转换为长度为N的序列。设定Y为L×K维的矩阵,元素为Aij,1≤i≤L,1≤j≤K。令Lp=min(L,K),Kp=max(L,K),若L (8) 在进行传统SSA算法测试的过程中发现,重组后的信号在起始和结束两端具有相位移动的现象,会对速度信号和位移信号的转换造成一定的影响,使信号出现失真现象。在不同信噪比和窗口长度的情况下进行测试得出:信号两端相移端点的长度M约为SSA窗长L的1/10。基于此,可以构建两段长度为M的伪数据xp1和xp2,分别添加在待测数据的两端,使得原始数据长度变为L+2M,然后再进行重组数据的SSA分解重构。 X+=[xp1,X,xp2] (9) 式(9)中,xp1和xp2可以为同一段数据。为了使伪数据更切合原始数据的特征,复制原始数据的前M个数据作为伪数据进行重组。 当信号的信噪比较低且信号存在高强度尖峰噪声时,SVD并不能完全分离噪声信号和有效信号,通常奇异值矩阵中会含有突变的奇异值,即噪声特征被当作趋势特征。 为解决奇异值突变问题,对分解后的奇异值矩阵进行曲线拟合,进一步消除残余噪声。有式(10): (10) 在曲线拟合时,按偏差平方和最小原则选取拟合曲线式(11): (11) 若使δi值最小,需依次求δi对aj的偏导式(12): (12) 在对奇异值降序排列后发现,通过选取前r个能量占比较高的奇异值进行信号重构,会取得较好的降噪效果,r值的选择通常根据主观经验进行选取,而r值的大小会对信号的处理结果造成很大的影响。改进的SSA算法中,使用M-K检验法自适应选择r值。 对X+进行SVD分解后可得奇异值向量U,令Uj=(U1,U2,…,UL-1),有式(13): (13) 式(13)中sgn为检验函数,令θ=Xk-Xj,如式(14): (14) 然后计算S的方差和M-K检验统计量Z[8]: 孔径分布和截留相对分子量采用一系列的PEG截留率结果并通过Matlab软件采用下述对数正态分布方程模拟计算得到[15]: (15) (16) 根据检验统计值可以得知:当Z>0时,检验序列呈上升趋势;当Z<0时,检验序列呈下降趋势;当Z=0时,检验序列保持原始数据的趋势,则可以根据此时r值的大小进行信号重构。 SSA改进算法的计算流程如下: (1)选定窗口长度L,确定伪数据长度M,分别添加至原始数据两端; (2)对重组的数据进行滞后排列,创建轨迹矩阵; (3)分解轨迹矩阵,获得奇异值和奇异值矩阵,并对奇异值降序排列; (4)对奇异值矩阵进行曲线拟合,去除突变奇异值; (5)预设定重构阶次r=1,进行趋势检验,若检验统计量Z值不为0,则r=r+1,直至Z值为0为止; (6)将轨迹矩阵映射至包含前r个奇异值的奇异值矩阵上,计算时间主成分; (7)求时间主成分矩阵的对角线平均,获得重构后的振动加速度信号。 利用计算机仿真验证所提改进SSA算法的有效性。实验中使用正弦信号,采样频率fs=2000Hz,采样点数N=1024。在信噪比为-20dB~20dB的环境下进行30000次的蒙卡特罗仿真模拟。假设加速度信号为含有高斯白噪声的正弦信号,可表示为式(17): s(t)=A×sin(2×π×f×t)+n(t) (17) 式(17)中,f为信号频率;n(t)为均值为0的高斯白噪声。 进行SSA分析之前,先消除因传感器温度等因素造成的零点漂移式(18): (18) 仿真中,f=20Hz,窗口长度L=300,伪数据长度M=30。SSA分析结果如图1所示,其中SNR=-4dB。对噪声信号依次进行了传统SSA,滑动窗长SSA(SSA-L),基于EEMD的SSA(SSA-E)和本文所提的改进SSA处理。 由图1可知,由于SSA强大的分解能力,经其处理后的信号不会存在谐波分量,更加平滑。传统的SSA算法和SSA-L算法,SSA-E算法所重构出的信号都存在相位移动;由于分解过程中的特征误选,导致部分信号能量提高或降低。而改进的SSA算法通过伪数据有效地解决了处理后的加速度信号在起始和结束两端的相位移动现象,改进后的奇异值能量趋于正常,误选几率降低,奇异值矩阵能够最大程度表述加速度信号的特征,使得结果更加逼近理想信号。 为了验证所提改进SSA算法的去噪效果,在信噪比为-20dB~20dB的环境下,求取了降噪后信号的信噪比如式(19): (19) 式(19)中,Ps为加速度信号的能量;Pn为噪声信号的能量。各算法降噪后的信噪比对比结果如图2所示。SSA分解中的奇异值突变,会导致部分噪声奇异值能量不能迅速衰减,从而被当作加速度特征进行分组。改进的SSA算法通过曲线拟合提高了有效信号的能量,同时优化了奇异值个数r的选择,极大地提高了信号的质量,尤其是在低信噪比的情况下,效果更为显著。 降噪质量的高低决定着是否能够准确获取相关的速度和位移等信息。对加速度信号进行一次积分和二次积分分别得到速度信号和位移信号。如图3和图4分别给出了SNR=-4dB时由加速度信号积分得到的速度信号和位移信号。由图3和图4可见,无论速度还是位移,改进SSA算法更逼近于无噪声环境下的速度和位移信号。 为了更直观地表述降噪后加速度信号的转换效果,使用式(20)求出了速度信号和位移信号的均方误差: (20) 最后,验证利用所提改进SSA算法由位移信号估计频率的正确性。对位移信号进行FFT,利用频谱峰值进行固有频率的估计,估计值如表1所示。在改进的SSA算法下,由于极大地提高了信号的信噪比,使得频率估计值和信号原始振动频率一致,低信噪比环境中的估计结果优于其他的SSA算法。说明使用改进的SSA算法降噪后的振动信号,携带的噪声分量更低,更利于估计结构体的固有频率,从而更有效地对结构体的工作状态和健康状况进行分析。 表1 频率估计(Hz) 传统的SSA算法在对原始加速度信号分解重构后,会存在相位移动现象,造成数据起始和结束两端失真,进而影响速度和位移信号的准确估计,并且在关键的重构阶次选择上没有选值标准,从而对信号的降噪效果产生较大的影响。基于M-K检验和最小二乘法的SSA改进算法针对传统SSA算法的缺点加以改进,同时保留了传统算法高效分解信号的优点。在相同的环境下,利用计算机仿真与传统SSA和其他改进算法SSA-L,SSA-E等降噪算法做了对比。仿真结果表明,基于M-K检验和最小二乘法的SSA改进算法在任何信噪比的环境下均优于其他几种算法,对建筑、桥梁等结构体的振动监测诊断提供了有效的信号处理方式。2 SSA算法优化
2.1 数据重组
2.2 奇异值拟合
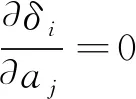
2.3 分组重构阶次的选择
2.4 改进算法的流程
3 实验仿真


4 结 语

