基于谐波平衡的三稳态压电振动能量采集器及其接口电路耦合动力学特性分析*

朱强国郑友成周 铄刘周龙王光庆张贝奇

(浙江工商大学信息与电子工程学院(萨塞克斯人工智能学院)，浙江 杭州 310018)

近年来，低功耗电子设备和器件(如无线传感器节点、通信节点、无人机、可穿戴、可植入电子产品等)的飞速发展，对其供电技术提出了严峻的挑战。传统电池供电因寿命短、不能够持续供能，且更换/维护/回收处理成本高等问题越来越无法满足上述供电需求。压电振动能量采集器(Piezoelectric Energy Harvester，PEH)是利用压电陶瓷的正压电效应采集器件工作中的环境振动能，并将其转换成电能的新型机电转换器件，因其结构简单、寿命长和能量转换密度高等优点成为微能源领域研究的热点。它有望代替电池实现对低功耗设备和器件的自供电[1-2]。

早期研制的压电振动能量采集器工作频带窄，在非共振区域效率较低[3]。为了提高能量采集器的输出性能，人们分别从采集器结构优化设计以及接口转换电路优化等方面开展了大量的研究。在采集器结构优化设计方面，采用非线性技术构造双稳态、三稳态以及多稳态压电振动能量采集器被证明能有效提高采集器的输出性能和转换效率[4-7]。Wang[8]和Yang等[9-10]基于三稳态压电悬臂梁模型，通过数值仿真与实验方法论证了三稳态压电能量采集器具有更宽的工作频带和更高的能量转换输出。Zhu等[11]研究了三稳态能量采集系统中不同势能阱的输出特性。然而，大部分能量采集器结构优化设计研究忽略了采集器与接口转换电路的耦合动力学特性，而是将接口转换电路和负载器件等效成为纯电阻，也就说这种等效负载电阻实现的交流供电。但在实际应用中，大部分的电子设备或可充电电池都需要直流电压给设备供电。因此，必须要通过接口转换电路将压电振动能量采集系统输出的交流电转化为直流电[12-14]。

接口电路的研究是提高能量采集器输出性能的另一个重要方面。当前，有四种主要的接口电路被广泛研究并应用于将能量采集器的电气输出从交流电压整流为直流电压，即标准二极管桥式整流滤波电路(SEH)、并联同步电感开关接口电路(PSSHI)、串联同步电感开关接口电路(S-SSHI)和同步电荷提取接口电路(SCE)[15-23]。然而，在大多数强调接口电路的研究中，采集器的机械性能和耦合条件很少受到关注。一方面，忽略机械性能和耦合条件可能会导致对采集器系统中某些细节的误解。另一方面，大多数强调接口电路的研究是基于接口电路直接串联或并联到线性能量采集器的模型，该线性能量采集器通常被视为等效于恒流源[23]。特别地，针对非线性压电能量采集器与非线性接口转换电路的耦合动力学特性目前还不多见[24-26]。Liu[24]和King等[25]研究了耦合优化SCE电路的双稳态能量采集器。Cheng等[26]提出了一种改进的具有可控最佳电压的P-SSHI电路(COV-PSSHI)，通过在存储器和电力负载之间使用电压控制策略来提高双稳态采集器的输出性能。为了进一步探明能量采集器性能的增强机理，有必要对非线性压电能量采集器及其非线性接口转换电路相互作用产生的耦合动力学特性进一步分析表征。

本文以非线性双自由度三稳态压电振动能量采集器及其二极管整流滤波接口转换电路为对象，基于能量法建立了系统的机电耦合动力学方程，利用谐波平衡法求解得到系统在谐波激励下的稳态动力学响应输出表达式及其稳定性判别矩阵——雅克比矩阵，仿真和实验分析激励加速度、负载电阻等因素对系统振幅和输出功率的影响以及对比外接交流电路和外接直流电路的影响。研究成果可以应用于可穿戴和植入设备、汽车和铁路系统、旋转机器、可再生能源系统和环境监测等设备中无线传感器节点的自供电系统，提高器件的使用寿命和安全性。

1 系统理论模型

图1所示为非线性双自由度三稳态压电能量采集器及其二极管整流滤波接口转换电路(简称ACDC接口转换电路)，双自由度三稳态压电能量采集器是由基座、弹簧、阻尼器以及三稳态压电能量采集器(TPEH，Tri-stable Piezoelectric Energy Harvester)组成。AC-DC接口转换电路由二极管整流桥、滤波电容和负载电阻构成。假设采集器悬臂梁的长度为L，其根部上下表面粘有长度为L1的压电片，磁铁A位于悬臂梁末端。磁铁B、C关于x轴对称地固定在U型基座右端上，其竖直距离为d g，与磁铁A水平距离为d。u2(t)、u1(t)和u0(t)分别为悬臂梁的绝对位移、U型框绝对位移和基础激励振动位移，其中¨u0(t)＝U0cos(ωt)为激振加速度，U0为振幅，ω为激振频率。M1表示U型框和两块外部磁铁的质量和，K1和C1分别表示弹簧刚度和阻尼器的阻尼。w(x，t)表示t时刻距离悬臂梁根部x处采集器相对于U型框的振动位移。以采集器悬臂梁根部中点建立直角坐标系统，水平方向为x轴，竖直方向为z轴。则有:

图1 三稳态压电能量采集器和接口电路模型

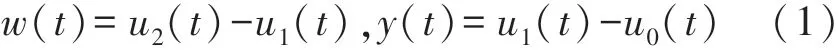
式中:y(t)表示U型框相对于基础激励的振动位移。

假设压电悬臂梁满足欧拉-伯努利梁理论，则采集器的振动位移可以写成:

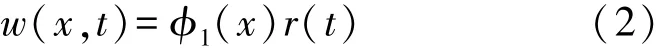
则系统动力学模型可以用能量法和Lagrange方程得到，系统的Lagrange方程可以表示为:

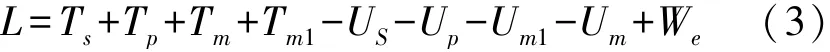
式中:T s、Us为基板的动能、势能；T p、U p为压电片的动能、势能；T m、Um为磁铁A的动能、势能，Tm1、Um1为M1动能、弹簧势能；W e为采集器输出的电能，其各自表达式表示如下:

式中:ρs，A s，b s，h s和ρp，A p，b p，h p分别为悬臂梁基板和压电片的密度、横截面积、宽度以及厚度；mt和I t是磁铁A的质量和转动惯量；E s、I s和E p、I p分别是基板和压电片的弹性模量和转动惯量；e31为压电应力常数；C p为压电片等效夹持电容；V p为采集器输出电压。

将式(4)～式(11)代入式(3)整理得到系统拉格朗日方程:

式中:

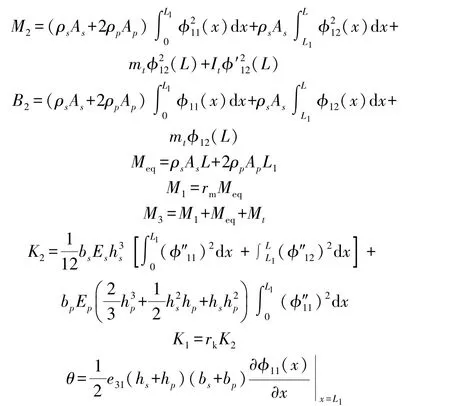
式中:rm和rk分别为系统质量比和刚度比；θ为系统机电耦合系数。

系统的广义耗散力和广义电流可以表示为:

式中:ω1为采集器谐振频率，ξ为阻尼系数，V(t)为接口电路输出电压。

则系统的动力学方程可以通过下面的方程进行推导

则动力学方程组为:

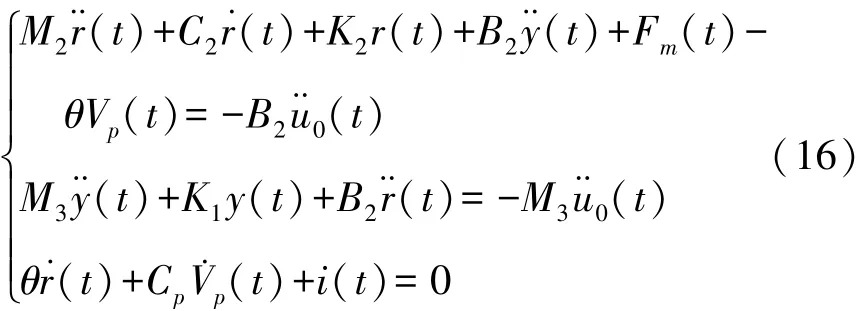
式中:C2＝2ξω1M2，F m(t)＝k1r(t)＋k2r2(t)＋k3r3(t)＋k4r4(t)＋k5r5(t)为三稳态采集器非线性磁力，系数k i(i＝1，2，…，5)可由磁铁A、B和C之间的几何位置关系和磁化强度获得。

①对于交流输出情况，即采集器两压电陶瓷直接外接负载电阻，V(t)＝V p(t)，则式(16)中电流可表示为:

②对于直流输出情况，即采集器两压电陶瓷接整流、滤波和负载电阻，如图1所示，当采集器外接电路为标准整流电路，i是通过二极管桥的电流，将电压整流为直流电压。此时V(t)＝Vr(t)，V r(t)是整流滤波电路输出电压。在一个周期中，整流桥交替导通和阻断。当｜V p｜＜V r时，电桥仍处于阻断状态，电路中无电流流过；当｜V p｜达到整流电压Vr时，整流桥就会导通，电路中有电流流过。整流桥从导通到阻断的状态切换发生在振动位移的最大点，也是速度的零交叉点。在本研究中，选取一个相对较大的滤波电容来获得近乎恒定的直流电压。因此，式(16)中电流表示为:

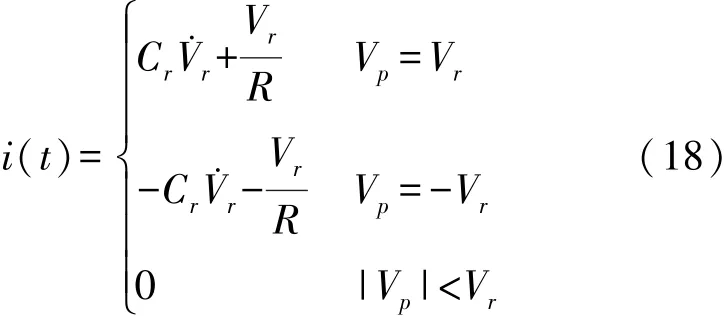
2 谐波平衡解及其稳定性分析

利用谐波平衡法对式(16)求解，假设系统的稳态解为:

式中:a0为平衡位置，振动位移幅值可表示为:

2.1 采集器外接AC-DC接口转换电路

当采集器外接AC-DC接口转换电路(亦称标准整流滤波电路)时，根据式(18)、式(19)可得出V p和V r之间关系为:

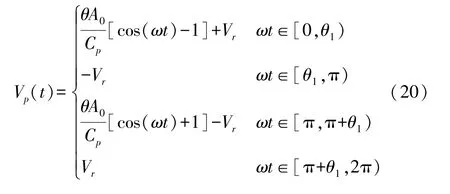
式中:θ1为二极管整流桥关断角。由式(20)解得:

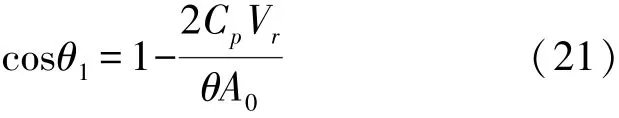
由于流经二极管的电荷量与消耗在负载电阻上的电荷量是相等的，则在半个周期内根据能量守恒原理得:

由于AC-DC电路二极管的通断导致采集器压电陶瓷两端电压V p是不连续的分段函数，无法采用谐波平衡法对系统方程求解。这里我们采用V p，f的基波信号代替V p进行求解，对陶瓷输出电压V p进行傅里叶变换，取其基波信号，其基谐波分量V p，f可以近似的为下式:

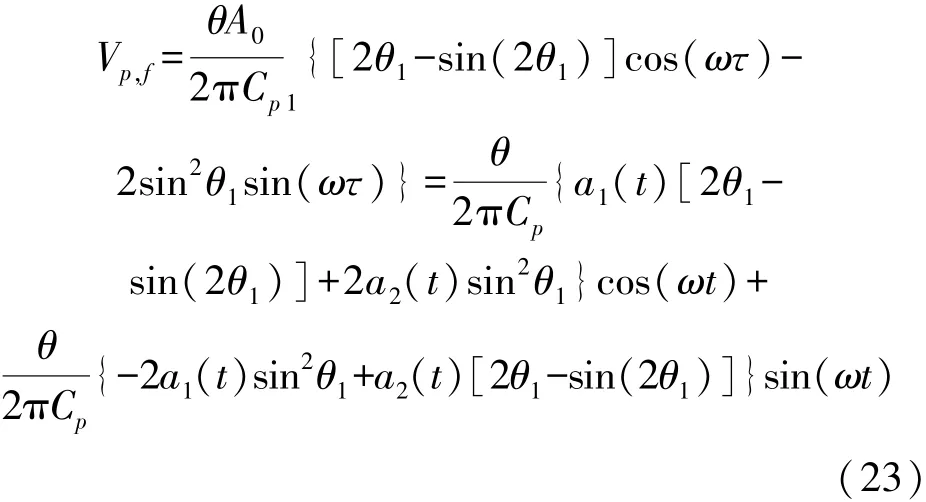
将式(19)和式(23)代入式(16)第一个式子中，令方程两边常数项、cos(ωt)和sin(ωt)的系数相同，并忽略高次谐波项以及二阶微分项得到:

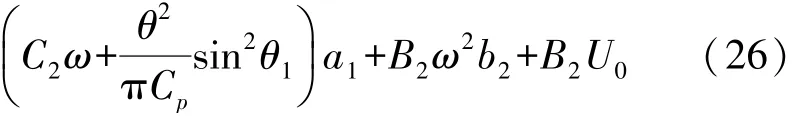
同理将式(19)代入式(16)第二个式子中并令cos(ωt)、sin(ωt)分别相等得到:

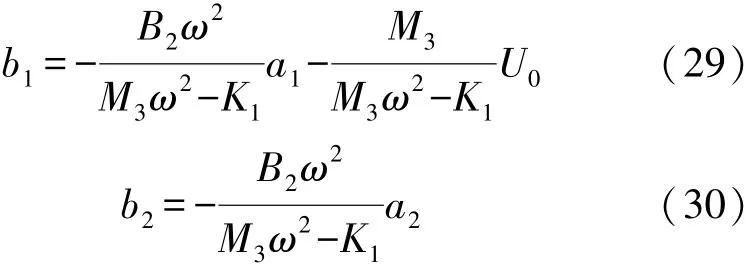
将式(29)、式(30)代入式(25)、式(26)中可得:

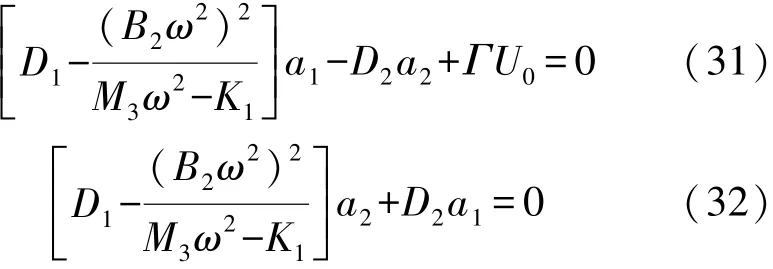
式中:

令

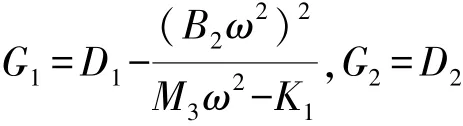
将式(31)和式(32)两边同时平方相加得到下式:

式(33)是以A0为变量的十次方程，解式(33)即可得系统稳态时振动位移振幅，将其代入式(22)可得直流输出电压V r，则AC-DC接口转换电路的有效输出功率为:

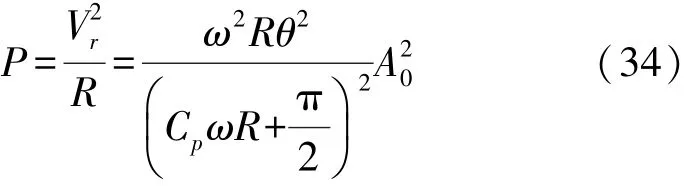
2.2 采集器直接外接负载电阻

当采集器直接外接负载电阻(亦称交流电路)时，则压电片两端电压可以表示为:

同理将式(19)和式(35)代入式(16)，利用谐波平衡法得到式(33)，其中得到D1、D2如下:

解式(33)后将结果代入上述表达式可得p1和p2，则电路有效输出功率为:

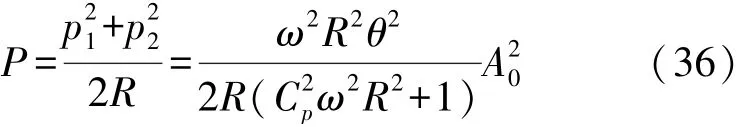
2.3 系统解稳定性分析与判断

系统解的稳定性通过雅可比矩阵J进行判断，如果该矩阵所有特征值实部均小于零，则为稳定解，否则为不稳定解。取向量α＝[a0a1a2b1b2]T，则式(24)～式(28)可写成

式中:

Q是5×1矩阵，每行对应着式(24)～式(28)中的右边，则雅克比矩阵J为:

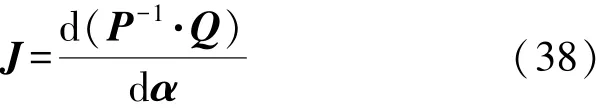
将由式(33)解得的位移幅值A0以及给定的系统参数和激励条件代入到式(38)中，判断其特征值的实部是否为负，即可判定其稳定性。

3 系统仿真分析

本节重点仿真分析系统参数、激励条件以及接口电路参数等对采集器输出性能的影响规律，获取采集器与接口之间的耦合动力学机理。

3.1 加速度幅值U0对系统动态特性的影响

当激励频率f＝10 Hz，磁铁间距d＝20 mm，外部磁铁间距d g＝10 mm，r m和r k都为16时，图2(a)～(c)是U0分别为2 m/s2、5 m/s2、10 m/s2时采集器振动位移的频响特性曲线，由图2(a)可见系统响应存在三个稳定解和两个不稳定解，实线和虚线分别是系统的稳定响应和不稳定响应。阱内运动稳定响应中有两处区域可以使系统做大幅度振动，分别在4.5 Hz附近和17 Hz～19 Hz，较低频率点为弹簧谐振频率，频带范围较窄，较高频率点为悬臂梁谐振频率，频带范围较宽。由图2可以看出，随着加速度U0的增大，阱内运动和阱间运动的幅值都基本不变，说明采集器的振动位移达到最大值。但阱间频带范围随着激励加速度U0的增大明显增大，并且能够引起阱间运动的最小频率在不断减小，分别在2.5 Hz～7.8 Hz、1.3 Hz～13.7 Hz和0.7 Hz～23 Hz。

图2 不同加速度(U0)下振动位移的频率响应曲线

3.2 磁铁间距d对系统动态特性的影响

当激励频率f＝10 Hz，激励加速度U0＝5 m/s2，外部磁铁间距d g＝10 mm，r m和r k都为16时，图3(a)～(c)是d分别为16 mm、18 mm、20 mm时振动位移的频响特性曲线，可以看出随着磁铁间距d的增加，阱间运动的频带范围增大，分别为2.1 Hz～9.5 Hz、1.5 Hz～11.7 Hz和1.3 Hz～13.6 Hz，且引起阱间运动的最小频率在不断减小以及振幅略有减小；对于阱内运动，引起较大振幅的弹簧谐振频率基本无变化(4.5 Hz左右)，而悬臂梁谐振频率明显左移，即悬臂梁的谐振频率变小，分别集中在36 Hz～40 Hz、24 Hz～28 Hz和16 Hz～20 Hz左右，可以看出当两处区域接近时，可以拓宽阱内运动的频带宽度。可见，适当的磁铁间距d可以使系统不仅更加容易进入大幅阱间运动而且增大了阱间运动频带范围，提高能量采集效率。

图3 不同磁体间距(d)下振动位移的频率响应曲线

3.3 质量比rm和刚度比rk对系统的影响

图4所示为激励频率f＝10 Hz，激励加速度U0＝5 m/s2，磁铁间距d＝20 mm，外部磁铁间距d g＝10 mm，刚度比r k＝16，质量比r m分别为1、10、20时振动位移的频响特性曲线。可以看出随着r m的增大，阱内运动弹簧谐振频率减小，悬臂梁谐振频率基本不变(16 Hz～19 Hz左右)；随着质量比的增大，阱间运动的频率范围分别集中在2 Hz～14.4 Hz、1.5 Hz～13.9 Hz和1.2 Hz～13.6 Hz，可见，增大质量比可以使采集器在更低的激励频率下进入阱间运动。

图4 不同质量比(r m)对频率响应曲线的影响

同样地，图5所示是质量比r m＝16，刚度比r k分别为1、10、20时振动位移的频响特性曲线。随着r k的增大，阱内运动弹簧谐振频率右移，频率分别集中在1 Hz、3.5 Hz和5 Hz左右；阱间运动频带范围分别在0.1 Hz～12.6 Hz、0.9 Hz～13.3 Hz和1.6 Hz～14 Hz，频带范围基本不变，但能够引起阱间运动的最小频率在增大，也就是说刚度比的增大并不利于系统在低频激励作用下进入阱间运动。

图5 不同刚度比(rk)对频率响应曲线的影响

3.4 外部磁铁间距d g对系统动态特性的影响

当激励频率f＝10 Hz，激励加速度U0＝5 m/s2，磁铁间距d＝20 mm，r m和r k都为16时，图6(a)给出了d g＝5 mm时的振动位移频率响应特性曲线，此时系统有两个稳定的平衡点和一个不稳定的平衡点，系统表现为双稳态运动特性；图6(b)～(c)分别是d g＝10 mm和13 mm时振动位移的频响特性曲线，此时系统均具有三个稳定的平衡点和两个不稳定的平衡点。随着外部磁铁间距d g的增大，阱间运动的频带范围明显减小，分别为1.3 Hz～13.7 Hz和2.7 Hz～7.4 Hz，且能够引起阱间运动的最小频率在增大以及振幅明显增大，这是因为随着外部磁铁间距d g的增大，突破势阱所需要的能量增加，采集器系统更难进入高能轨道振动状态；对于阱内运动，弹簧谐振频率基本不变(4.4 Hz左右)，而悬臂梁的谐振频率在增大，分别在16 Hz～19 Hz、22 Hz～25 Hz左右。

图6 不同外部磁体间距(d g)下振动位移频率响应曲线

3.5 负载电阻R对系统动态特性的影响

当激励加速度U0＝5 m/s2，d＝20 mm，d g＝10 mm，rm＝r k＝16时，由图2(c)可知系统在激励频率f＝1.3 Hz～13.7 Hz内作阱间运动，其振幅随着频率增大而增大，但是其中f＝4.35 Hz～4.45 Hz时，系统处于弹簧谐振频率，其振幅远大于其他频率下的振幅；当激励频率f＞13.7 Hz时，只有阱内运动，其振幅随着频率增大而减小。基于图2(c)的仿真结果，图7(a)、(b)所示是不同激励频率f＝[2 4.3 4.4 12 17 18]Hz下，负载电阻R与整流电压V r以及功率P之间的关系曲线。由图7电压曲线可以看出:随着电阻R的不断增大，输出电压快速增大到某个值后趋于稳定。随着激励频率的增大，整流电压呈现先增大后减小的变化趋势。从图7功率曲线可以看出，随着负载电阻的增大，输出功率呈现先快速增大再缓慢减小的变化曲线；随着激励频率的增大，输出功率变化趋势和整流电压的变化趋势相似，先增大后减小。当负载电阻与采集器阻抗完全匹配时，采集器输出功率达到最大值，此时负载电阻为最优负载电阻。从图7功率曲线中还能看出随着激励频率的增大，最优负载电阻的阻值在不断减小。

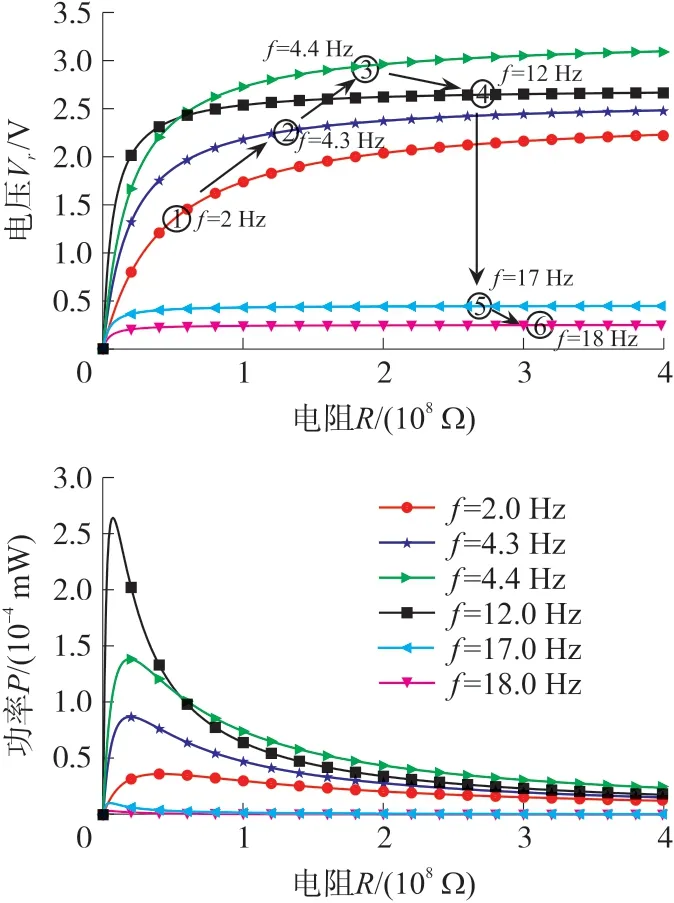
图7 不同频率下整流电路中负载电阻和电压、功率之间的关系

3.6 机电耦合系数θ对系统的影响

根据式(12)中机电耦合系数θ方程中可知，机电耦合系数主要由压电应力常数e31决定，它是反应压电能量采集器机械能转换电能能力的主要参数。取θ＝5.38×10-8、θ＝5.38×10-6和θ＝5.38×10-3，分别表示三种耦合情况，即:弱耦合、中耦合和强耦合，研究3种耦合条件下机电耦合系数对系统振动位移、整流电压和输出功率的影响，如图8所示。由图8可以看出:在一定范围内(耦合系数θ从5.38×10-8到5.38×10-6)，随着耦合系数不断增大，系统的位移幅值基本上没有变化但是输出电压和功率明显增大；当耦合系数过大时，即耦合系数达到θ＝5.38×10-3时，系统的振动位移幅值大大降低，阱间运动完全消失，只存在阱内运动。但是，当激振频率f位于4.43 Hz～4.45 Hz频带范围内时，阱内运动具有较高的振幅、输出电压和功率。整流电压和输出功率则随耦合系数的增大呈现先增大后减小的变化趋势。这是因为随着耦合系数的增大，机械能转移到电能的占比增大，但是也降低了每个振动分支的响应振幅，也就是说悬臂梁的机械能更少，所以在适度的耦合系数范围内，具有更高的输出电压和功率，而更大的耦合系数导致较低的振幅、输出电压和功率。

图8 不同耦合系数(θ)下系统振动位移、整流电压和输出功率的频响特性

3.7 整流电路接口和交流电路接口对比

图9显示了标准整流电路和交流电路情形下系统振动位移和输出功率的动态响应输出结果，机电耦合系数θ＝5.38×10-7。由图9(a)能够看出外接交流电路和标准整流电路的位移幅度几乎相同。在图9(b)中，标准整流电路的收获功率略低于交流电路的平均功率。这是因为在标准整流电路中，部分转换后的电能被二极管损耗掉了，导致负载电路消耗的功率略有降低；而所有流入交流电路的转换电能都被电阻性负载消耗掉了。

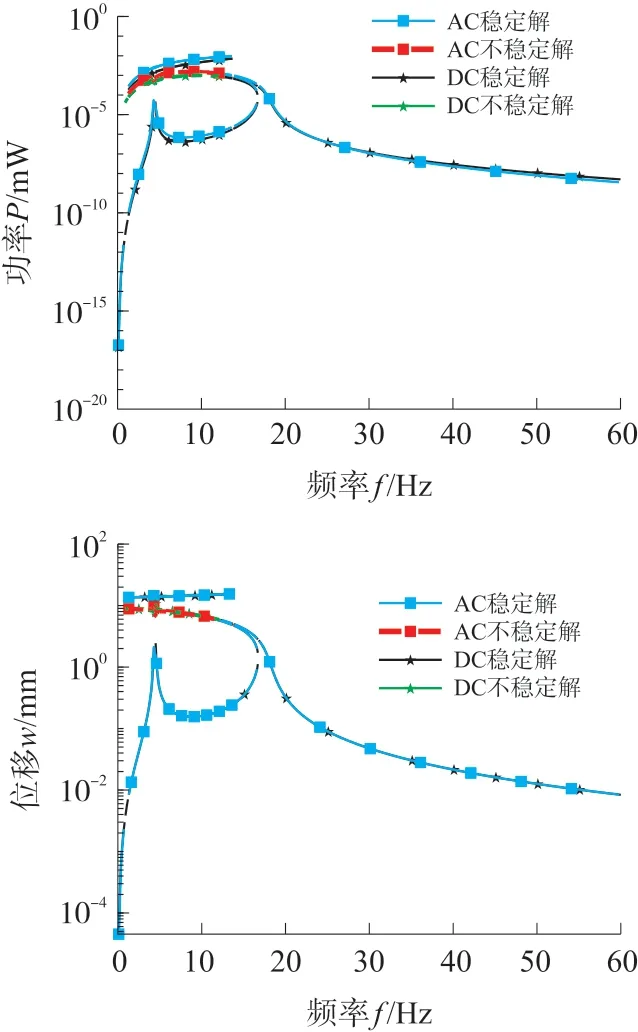
图9 标准整流电路与交流电路接口系统中频响特性

图10是两种电路连接下采集器输出动态特性随耦合系数的变化规律。由图10可见，在适当耦合系数(θ＜6×10-6)范围内，系统存在阱间运动和阱内运动共存的现象，此范围内采集器的振动位移幅值随耦合系数的增大保持不变，表明小的耦合系数对采集器的振动位移影响较小。标准整流电路条件下采集器阱间运动的耦合系数范围(1×10-8＜θ＜7×10-6)比交流电路的范围(1×10-8＜θ＜6×10-6)要略宽一些，但其输出功率要比交流电路的输出功率略低些，因此在这个范围内，交流电路可以提取更多的电能；但是在相对较高耦合系数(θ＞9.5×10-5)的情况下，系统只存在阱内运动，耦合系数对振幅影响明显，随着耦合系数的增大，阱内运动的响应振幅明显下降，且标准整流电路的动态响应振幅和功率都要高于交流电路，此情况下标准整流电路比交流电路获得更多的电能。

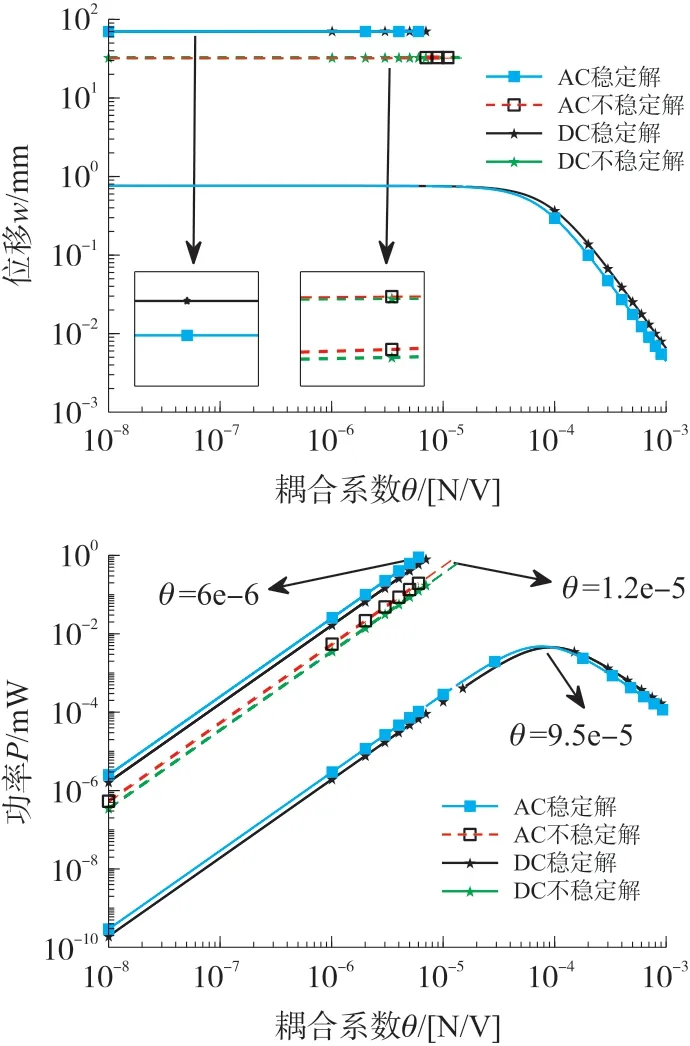
图10 标准整流电路和交流电路接口系统中耦合系数与响应振幅和收获功率上的比较

3.8 电路输出波形分析

为了进一步研究系统的充放电过程，当激励频率f＝6.5 Hz，磁铁间距d＝20 mm，外部磁铁间距d g＝12 mm，r m＝r k＝16，图11(a)和图11(b)分别是采集器阱间运动和阱内运动的振动速度、陶瓷输出电压和整流电压以及输出电流的波形图，其激励加速度分别为U0＝6 m/s2(阱间运动)和U0＝0.3 m/s2(阱内运动)。结果表明，一个振动周期中的陶瓷输出电压和输出电流可以分为两个阶段，在(0，θ1)和(π，π＋θ1)期间为放电阶段，陶瓷输出电压小于整流输出电压，整流二极管截止，此时电路中电流i＝0，在(θ1，π)和(π＋θ1，2π)期间为充电阶段，陶瓷输出电压高于整流输出电压，整流二极管导通，此时电路中电流存在；当系统达到稳定状态后，其整流电压基本保持不变，但阱间运动的整流电压远大于阱内运动，分别为3.1 V和0.23 V，其输出电流也远大于阱内运动的输出电流。这种充放电现象在交流电路中是无法观察得到的。

图11 数值模拟阱间运动和阱内运动的动态响应、电压和电流的数值波形

4 实验研究与结果分析

为了验证本文数学模型和仿真结果的正确性，研制了双自由度三稳态能量采集器实验样机，如图12(a)、12(b)所示。两块相同的压电片贴附在材料为不锈钢的悬臂梁上下表面，其末端粘有一个永久磁铁，在U形槽的右端固定着两个完全相同的外部磁体，其磁场方向与悬臂梁末端磁体相斥。U形槽与底表座之间连接一弹簧，为弹性放大器，外接AC-DC接口转换电路。采集器实验系统如图12(c)所示，模拟环境振动的谐波信号由信号发生器产生，经功率放大器放大后，驱动振动器来模拟简谐运动。采集器悬臂梁的末端位移由位移传感器测量得到，输出电压经过二极管，输出电压以及整流后的电压可以通过示波器获取，最后将所获取的所有信号送入动态信号分析仪分析输出。

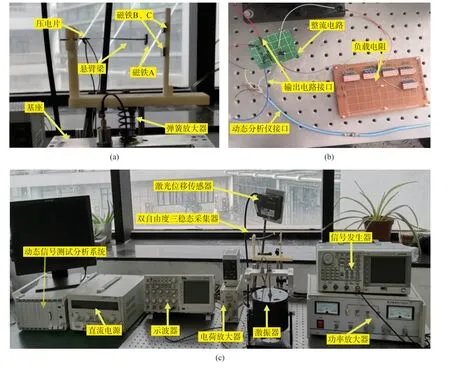
图12 双自由度三稳态样机(a-b)和实验测试系统(c)

取U0＝5 m/s2、d＝20 mm和r m＝r k＝16，图13所示是外部磁体间距d g分别为10、13、15 mm的位移幅值、电压和功率响应实验结果，可以看出实验结果与理论仿真结果基本吻合；随着外部磁体间距的增大，阱间运动的频带宽度明显减少，直至消失；阱内运动两个谐振峰之间的间距逐渐增大。

图13 不同外部磁体间距下，实验与仿真的频响特性对比

进一步实验研究了激励加速度U0分别为5和10 m/s2作用下采集器振动位移、输出电压和功率响应特性，如图14(a)、14(b)所示，可以看出随着激励加速度的增大，阱间运动的频带范围明显增大，且能够引起阱间运动的最小频率在减小；而对于阱内运动而言，基本上无变化，激励频率f为5Hz和17Hz时存在较大振幅。

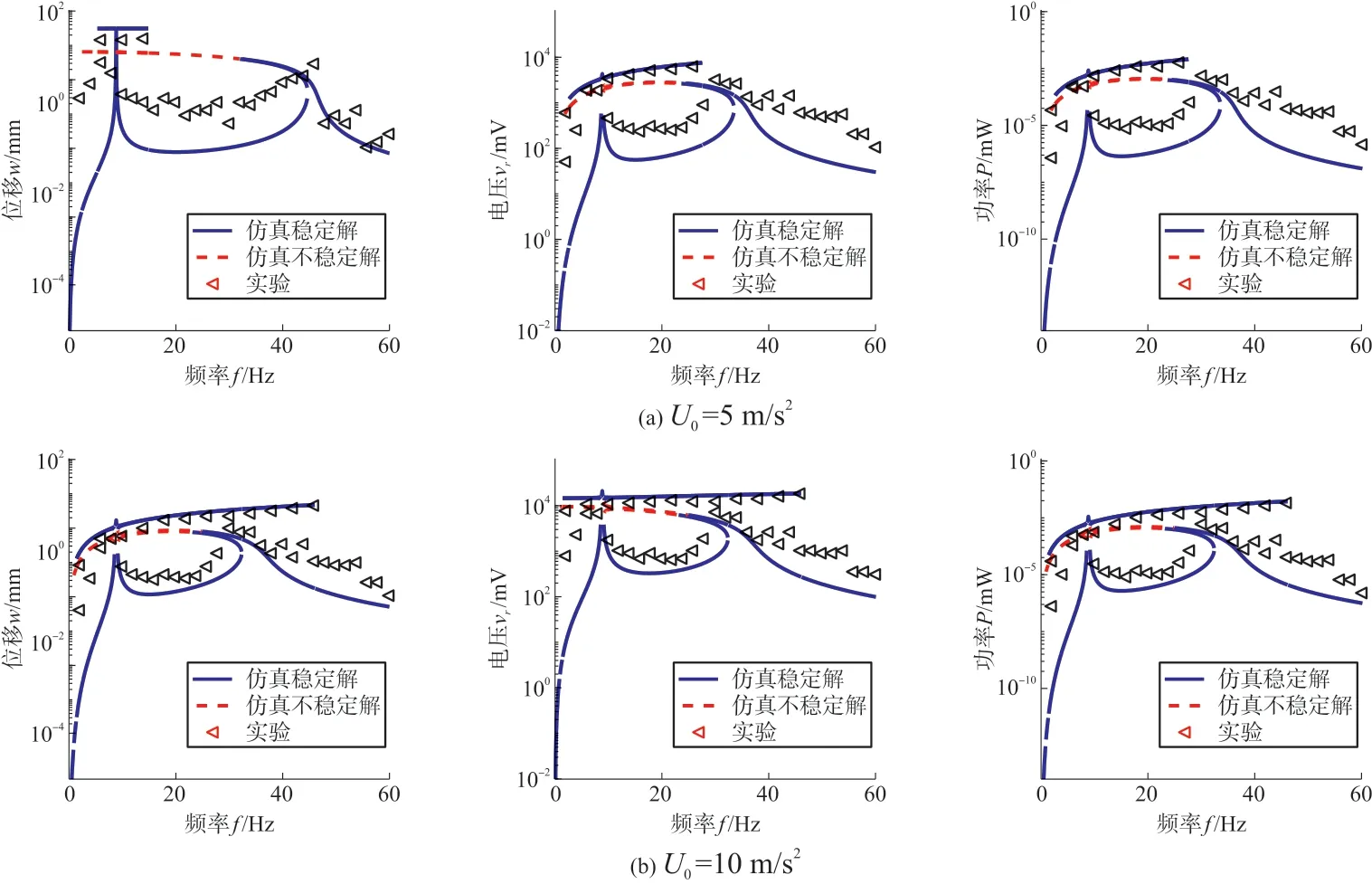
图14 不同加速度下，位移、电压和功率的实验与仿真的频响特性对比

实验获得的接口电路波形如图15所示。可以看出在一个振动周期内有两处存在三个波峰和两个波谷，即三个稳定点和两个不稳定点；压电片输出电压存在充电和放电的过程，经过整流电路后的整流电压最后稳定在2.6 V，满足部分低功耗电子产品的供电需求。实验与仿真结果产生的误差如下:①实验中弹性放大元件受基础激励时同时产生垂直及前后的俯仰振动，振动幅度越大，俯仰振动导致的倾斜角度越大，从而导致激光位移所测振动速度偏大；②实验中整流电路中的二极管存在0.5 V～0.7 V的压降，而仿真中二极管被视为理想二极管，导通压降为0，所以数值仿真输出电压结果比实验结果偏大些，误差在0.6 V左右，可见实验与数值仿真基本一致。

图15 阱间运动的动态响应与电压的数值模拟和实验比较

5 结论

本文建立了双自由度三稳态压电能量采集系统的非线性机电耦合运动方程，对其振动特性以及输出功率进行了研究分析，仿真实验验证了本文方法的正确可行性，得到如下结论:

①适当的磁铁间距(d)、外部磁铁间距(d g)、质量比(r m)和刚度比(r k)以及激励加速度(U0)可以提高能量采集系统的输出特性，此外对阱内运动而言，当弹簧谐振频率和悬臂梁谐振频率接近时，大振幅具有较宽的频率带宽。

②参数研究显示较高的耦合系数θ会影响阱间运动的有效带宽。在适当的耦合系数和负载电阻的范围内，通过增大耦合系数或负载电阻可以获得更高的电压和功率。而在相对较高的耦合系数和负载电阻范围内，增大耦合系数或负载电阻将导致较小的电压和功率。此外，最佳的负载电阻取决于激励频率且随着激励频率的增大而减小。

③在弱耦合系数下，振幅变化不大，交流电路的输出功率高于标准整流电路；而对于相对较高的耦合系数，标准整流电路的振幅要高于整流电路接口的振幅，且随着耦合系数的增大而明显减小，且交流电路的功率要高于整流电路的功率。

④实验获得的2.6 V直流输出电压完全满足部分低功耗电子产品(无线传感器节点、通信节点)的供电需求。

研究成果可应用于公路、铁路轨道、车辆减震器、海浪、风和人体运动等等振动环境中，实现较低频、低激励条件下振动能量的有效采集和转换，为低功耗电器或设备提供稳定的直流供电。