应用于电动汽车充电桩的VSG建模与分析

孙宇新，王 宇，施 凯，徐培凤

（江苏大学 电气信息工程学院，江苏 镇江 212013）

0 引言

电动汽车推广作为应对气候变化问题的潜在解决方案，其渗透率呈指数级增长。一方面，电动汽车以其产生废气少静谧性好的优势，正逐步取代传统内燃机汽车在交通领域的地位。另一方面，电动汽车在分布式电源和电网能量管理中间扮演着重要的角色，成为电网用电低谷期潜在的储能对象，并能在高峰期向电网送电，起到削峰填谷的作用［1］。然而电动汽车也被认为是电网的附加负载，可能会对电网设备造成过载，干扰电网电压的运行稳定性，并产生谐波。并且随着电动汽车的日益普及，电动汽车充电桩的负面影响将会变得越发显著。分布式电源通过电力电子变换器与电网进行联接［2］，大规模的电力电子器件使得电网呈现一种“低惯性”的特点，缺乏物理的惯性和阻尼［3—4］。为此有学者提出将虚拟同步发电机（virtual synchronous generator，VSG）技术应用于电动汽车的充电领域，通过模拟传统同步发电机调频调压的方式为系统提供可变的惯性和阻尼，从而实现电动汽车充电桩的友好并网，提高电力系统的稳定性［5］。

然而，VSG也是由脆弱的电力电子器件构成，可能出现频率共振、输出功率振荡等不良特性。这些现象会降低VSG的性能，甚至会导致系统不稳定［6—7］，因此有必要对VSG的输出阻抗进行建模分析。文献［8］采用基于状态空间的小信号建模方法，通过特征值和灵敏度分析了VSG的控制参数对系统稳定性的影响。但是其中涉及的变量太多，如果考虑并联单元，系统整体矩阵的阶数将成倍增加，这对建模和计算的可行性提出了挑战。文献［9］通过建立VSG在同步旋转坐标系（synchronous rotating reference frame，SRRF）下的小信号数学模型，分析了不同电网强度下VSG的并网稳定性。然而，交流系统不平衡时，小信号系统的稳定工作点不再是直流常数，此时DQ轴阻抗建模的方法已不再适用。文献［10］用谐波线性化［11］的方法对VSG进行序阻抗建模，把正负序当作独立的解耦分量，但是并未考虑可能出现的频率耦合关系。

本文在考虑频率耦合的基础上，用谐波线性化的方法对VSG进行序阻抗建模。借助推导出的解析模型，分析不同的控制参数、不同的电网强度和系统稳定性之间的关系。最后仿真结果证实了本文理论分析的正确性和建模方法的有效性。

1 VSG拓扑与控制

虚拟同步发电机的拓扑结构如图1所示。图1中Vdc为VSG的直流侧电压，一般认为是稳态值；ea、eb和ec为VSG的内电势；ia、ib和ic为VSG的输出电流；va、vb和vc为VSG的输出端电压；Lf、Cf和Rf分别为VSG的滤波电感、滤波电容和阻尼电阻；Lg为电网的线路电感；vga、vgb和vgc为电网电压。

图1 VSG主电路拓扑Fig.1 Main circuit topology of VSG

VSG的有功控制器模拟了同步发电机的惯性和一次调频特性；无功控制器模拟了同步发电机的一次调压特性。图2为VSG的控制结构，电压控制型VSG的有功控制器和无功控制器的数学方程如下

图2 VSG控制结构Fig.2 Control strcture of VSG

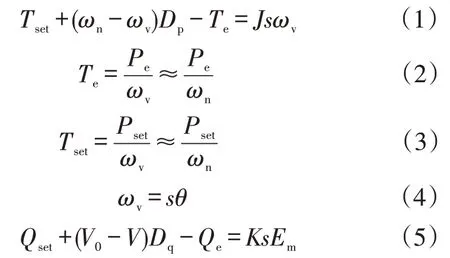
式中：J为虚拟转动惯量；ωv、ωn分别为VSG的输出角频率和电网的额定角频率；Tset、Te分别为转矩给定和电磁转矩；Dp、Dq分别为有功阻尼系数和无功阻尼系数；Pset、Qset分别为有功功率和无功功率给定；Pe、Qe分别为瞬时输出有功功率和无功功率；θ为VSG内电势的相位；K为无功惯性系数；V0、V分别为VSG额定电压和输出电压的幅值；Em为VSG的内电势。

VSG的输出有功功率Pe和无功功率Qe可根据瞬时功率理论计算得到，其计算公式为

式中：vd和id分别为d轴的输出电压和输出电流；vq和iq分别为q轴的输出电压和输出电流。

VSG的调制波由有功控制器和无功控制器的输出共同决定，其表达式为

式中：eam、ebm和ecm为VSG的调制波。

由图1可知，VSG的内电势、输出端电压和输出电流的表达式为

2 频率耦合效应

由于VSG中包含了功率计算器和功率控制器，此时若在VSG公共耦合点处引入一个频率为fp的扰动量，根据傅里叶级数理论［12—13］，可以将不同变量中的扰动分量频率表示为mfp+nf1，这里f1为基波频率。对于线性分析，可以忽略“m”不为1的非单位分量。在稳态运行时，三相系统会有一个在频率+f1处的正序分量，该分量等价于在频率-f1处的负序分量。这时，三相变量中存在的主要频率分量为在fp+f1下的正序和在fp-f1下的负序［14—15］。

因此在时域中，加入小信号扰动的A相电压电流可以写成如下形式

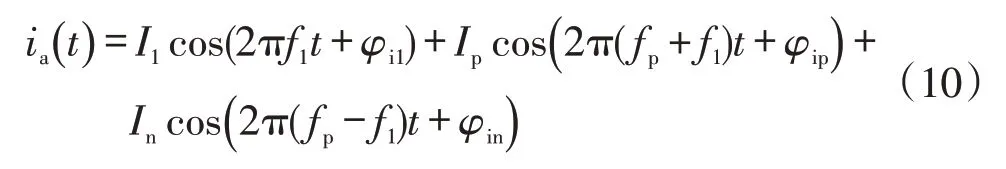
式中：V1、Vp和Vn分别为基波电压、正序扰动电压和负序扰动电压的峰值；I1、Ip和In分别为基波电流、正序扰动电流响应和负序扰动电流响应的峰值；φvp和φvn分别为正序扰动电压和负序扰动电压的初相角；φi1、φip和φin分别为基波电流、正序扰动电流响应和负序扰动电流响应的初相角。

在频域中，电压va和电流ia可以写成如下形式

式 中：V1=V1/2；Vp=(Vp/2)e±jφvp；Vn=(Vn/2)e±jφvn；I1=(I1/2)e±jφi1；Ip=(Ip/2)e±jφip；In=(In/2)e±jφin。

扰动电压和扰动电流之间的频率耦合关系可以用如下的2×2导纳矩阵YPN来表示

3 频率耦合特性建模

将上述电压电流的频域表达式经过Park变换后可以写成如下形式

将式（14）—式（17）代入式（6），并利用频域卷积定理可得有功功率和无功功率在频域的表达式为

式 中：I2=(I1/2)e±j(φi1-π/2)；Idr=I1cos φi1；Iqr=I1sin φi1，上标“*”表示复数的共轭。

根据VSG有功控制器可得θ的表达式为

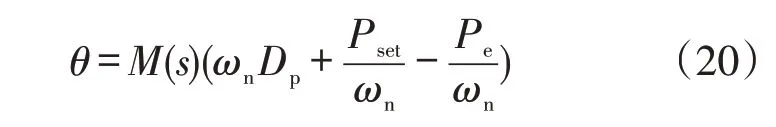
式中：M(s)=1/(Js2+Dps)。

将式（18）代入式（20），可以得到θ在频域里面的表达式为

在VSG的三相调制波相角θ中引入相角扰动Δθ，即θ=θ1+Δθ。θ1为基波分量相角，Δθ是由扰动电压引起的小扰动量，所以由式（18）可以得到Δθ的频域表达式如下

由于Δθ为小扰动量，因此通过近似处理可得

将式（22）代入式（23），可以求出sin θ的频域表达式为

同理，根据VSG无功控制器可得Em的表达式为

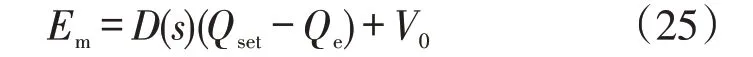
式中：D(s)=1/(Ks+Dq)。

将式（19）代入式（25），可以得到Em在频域里面的表达式为

联立式（24）和式（26）可得E*在频域里面的表达式。将E*通过虚拟阻抗送入如图2所示的准PR控制器，图2中GPR(s)为准PR控制器的传递函数，Kid为电流调节系数，求出内电势ea在频域里面的表达式，最终进一步可以求得阻抗表达式如式（27）—式（30）所示。

4 仿真验证

为了验证提出的阻抗数学模型，根据图1的VSG结构在Matlab/Simulink里面搭建了一个时域仿真模型。

图3为Zpp与Zgp，Znn与Zgn的输出阻抗特性曲线，两者可以很好的吻合，证明了阻抗建模的正确性。

图3 VSG正负序阻抗理论曲线和仿真结果Fig.3 Theoretical and simulation results of VSG positiveand negative-sequence impedance

图4为Lv取值变化时VSG的输出阻抗特性曲线。从图4中可以看出，随着虚拟阻抗取值变大，在中高频段VSG的输出阻抗幅值明显增加，放大了高次谐波对系统的影响，同时在基频处，随着虚拟阻抗增大，输出阻抗相位裕度减小，降低了系统的鲁棒性。由此可见，虚拟阻抗取值过大时可能会导致系统不稳定。

图4 Zv增大时VSG正负序阻抗频率响应曲线Fig.4 Frequency responses of VSG positive-and negativesequence impedance when Zv increases

由于导纳矩阵里面的非对角线元素不可以被忽略，所以必须采用如下的广义奈奎斯特判据形式［16—17］

式中：Zg=diag{ }j2π(fp+f1)Lg,j2π(fp-f1)Lg；I为单位矩阵。

电网强度的划分通过系统的短路比（short circuit ratio，SCR）来确定，它的定义如下

式中：SSC为电网公共连接点处的短路容量；SN为电网接入设备的额定容量。通常情况下SCR大于20的电网认为是“强电网”，SCR小于6～10的电网认为是“弱电网”。

图5为电网电感值从4 mH（SCR=16）变化到15 mH（SCR=4）时YPN*Zg的特征根轨迹。可以看出，奈奎斯特曲线均没有包围（-1，j0）点，系统始终保持稳定状态，图6的电流仿真波形也证实了这一点。进而说明了VSG技术在电动汽车充电并网时通过提供可调的惯性和阻尼提高了车网系统的鲁棒性。

图5 SCR变化时特征根奈奎斯特曲线Fig.5 Nyquist curves of characteristic roots when SCR changes

图6 Lg变化时PCC电流波形Fig.6 PCC current curves as Lg changes

5 结束语

通过对应用于电动汽车充电桩的VSG技术进行了建模与分析，用谐波线性化的方法建立了VSG的阻抗模型，揭示了不同控制参数和电网强度下系统稳定性的变化，从而优化电动汽车充电桩对电力系统产生的不良影响，实现分布式电源的友好并网。D