基于灰色关联-逐步回归的我国政府债券发行量研究

那园园，赵东学

（牡丹江师范学院 数学科学学院，黑龙江 牡丹江 157011）

国家通过发放政府债券进行基础建设，债券发行量与各种经济数据相关.［1］本文综合运用灰色关联分析与逐步回归分析法，对其影响因素及发展趋势进行研究.

1 政府债券发行量影响因素灰色关联分析

基于2021年中国人民银行统计数据，对1年期中债国债收益率（X1）、1年期Shibor利率（X2）、金融债券发行量（X3）、股票市场上证综合指数（X4）、股票市场深证成份指数（X5）、公司信用类债券（X6）、国际机构债券（X7）等的发行量指标进行统计分析.［2-4］

建立分析数列参考数列为我国2021年的政府债券发行量，即y={y(k)|k=1，2…12}.影响参考数列的比较数列为1年期中债国债收益率、1年期Shibor利率、金融债券发行量、股票市场上证综合指数、股票市场深证成份指数、公司信用类债券、国际机构债券，记为x={xi(k)|k=1，2…12；i=1，2…7}.

数据无量纲化处理采用每个数据列的数据xi(k)，k=1，2…12；i=1，2…7，除以对应列的第一个数据xi(1)，将数据列作初值化变换，数据保留小数点后三位.

关联系数及关联度设ξi(k)i=1,2…7；[k=1,2…12]为xi(k)对y(k)在k时刻的关联系数，分辨率ρ取0.5.［5］为了使分散信息集中化，取各列的平均值作为曲线xi(k)对曲线y(k)在k时刻的关联度，记为ri，i=1，2…7.可以得到各因素与政府债券发行量间的关联度均大于0.5，且关联度的排序为r1＞r3＞r2＞r5＞r4＞r6＞r7，即1年期中债国债收益率＞金融债券发行量＞1年期Shibor利率＞股票市场深证成份指数＞股票市场上证综合指数＞公司信用类债券＞国际机构债券.说明1年期中债国债收益率是影响我国政府债券发行量最关键的因素；1年期中债国债收益率和1年期Shibor利率之间的关联度相差无几，且与政府债券发行量关联度相对较低；排除正影响和负影响的因素，在分析政府债券发行量时应当注意公司国际机构债券和信用类债券对其的影响.［6］

2 逐步回归分析法在政府债券发行量的应用

政府债券发行量的线性回归分析.利用SPSS软件进行逐步回归：

第一，建立对逐步回归模型变量的输入与剔除过程（表1）.模型最先引入的变量是股票市场上证综合指数，再引入1年期中债国债收益率［7］，说明在逐步回归的过程中，股票市场上证综合指数和1年期中债国债收益率之间不存在多重共线性，引入变量会使变量之间产生多重共线性，影响研究结果.

表1 输入/移去的变量

第二，建立模型拟合优度检验（表2）.模型1的调整R2为0.543，模型2的调整R2为0.809，模型2更接近于1，说明模型2拟合程度更好.

表2 模型汇总

第三，建立方差分析表（表3）.表3的结果表明，模型2更为合适，P值为0.000，在显著性水平为0.01情况下，可以认为政府债券发行量与1年期中债国债收益率和股票市场上证综合指数之间有线性关系.

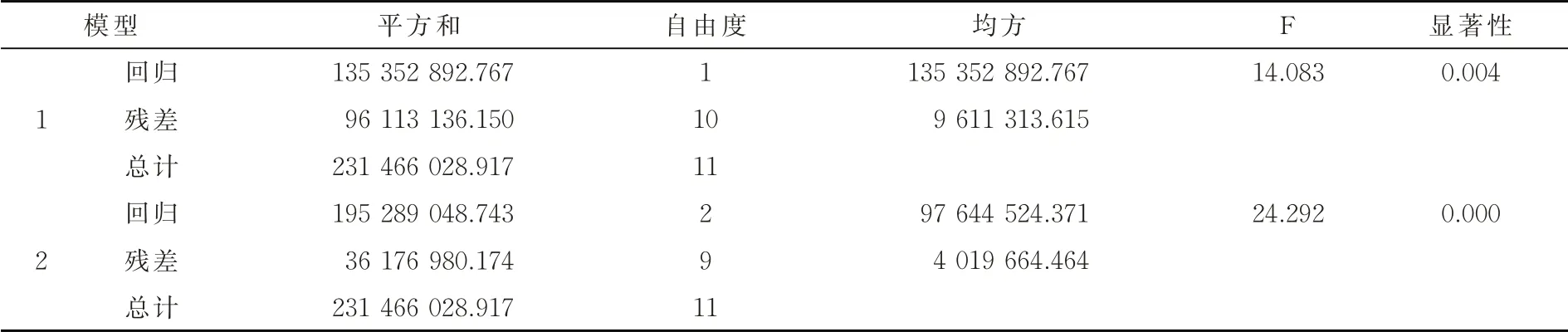
表3 ANOVA

第四，建立逐步回归分析预测模型的系数分析表（表4）.

表4 回归模型的系数

考虑数据量纲的不同，选择非标准化系数作为回归系数.根据模型2建立逐步回归方程.

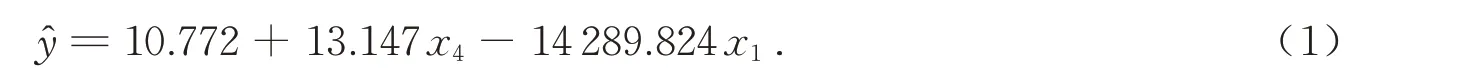
式（1）中，̂表示政府债券发行量，x4表示股票市场上证综合指数，x1为1年期中债国债收益率.

经检验，P值为0.000，按照给定的显著性水平为0.01的情况下，回归方程有显著意义.且x4的偏回归系数为正，说明政府债券发行量和股票市场上证综合指数之间是正线性关系.x1的偏回归系数为负，说明政府债券发行量和1年期中债国债收益率之间是负线性关系.

第五，对模型进行残差检验.利用SPSS软件，以政府债券发行量为因变量，对逐步回归模型建立观测的累积概率对期望的累积概率的回归标准化残差图（图1）.标准化残差散点的分布在整体上均靠近直线，可以判断标准化残差呈正态分布，说明所建立的回归方程通过了显著性检验，回归方程与原始数据的拟合效果很好.

图1 回归标准化残差的正态P-P图

将2021年1至11月的股票市场上证综合指数和1年期中债国债收益率代入式（1），可得2021年1至11月的政府债券发行量的误差分析（表5）.表（5）的结果表明，绝对误差的均值为1419.525564，相对误差的均值是8.23%，将预测值与真实值进行对比，预测值是合理的，可以基于股票市场上证综合指数和1年期中债国债收益率的数据，利用逐步回归的模型对未来我国政府债券发行量进行预测.

表5 政府债券发行量的误差分析

3 总结

本文综合灰色关联分析法与逐步回归分析方法，对我国政府债券发行量进行分析，其中1年期中债国债收益率和股票市场上证综合指数对政府债券发行量影响较大，具有一定的促进作用.进一步可以采用逐步回归分析方法，通过建立的回归模型，对政府债券发行量进行预测.