抱持式车辆搬运器转臂冲击性能的研究
李其朋,卢乐鹏,陈岁繁,梁 明
(1.浙江科技学院机械与能源工程学院,浙江 杭州 310023;2.杭州智泊科技有限公司,浙江 杭州 310000)
1 引言
智能化立体车库已经成为大城市解决“停车难”问题的主要选择,具有越来越广阔的发展前景[1-3]。车辆搬运器属于智能化立体车库中最核心的部件,负责自动化的搬运汽车[4]。抱持式车辆搬运器属于车辆搬运器的一种,因速度快、效率高等优点,得到广泛的应用[5]。车辆搬运器的转臂在工作过程中需要承受较大的载荷,故目前的研究主要以承受工作载荷为主[6-8],从而忽略了转臂在转动过程中所受的冲击问题,这对搬运器的寿命有很大影响。因此,对其冲击的研究具有重要的意义。
设备冲击的研究方法通常有试验研究、数值计算和解析法[9-10]。文献[11]采用试验研究的方法测试得到了柴油机加速度响应曲线。文献[9]分别利用了试验研究和数值计算相方法获得不同方向冲击下救生弹射座椅的加速度响应曲线。文献[12]用解析法分析立辊轧机冲击振动加速度信号,得到加速度的解析表达式。采用解析法对抱持式车辆搬运器的转臂机构进行研究,不仅能获得加速度响应曲线,还可获得各参数和加速度冲击之间明确的函数关系,更有利于分析抱持式车辆搬运器转臂的加速度冲击影响因素。最终得到无加速度冲击的槽型曲线。
2 模型简化
抱持式车辆搬运器工作时,先收拢转臂进入汽车车底,然后展开转臂通过对汽车车轮的抱持带动汽车整体抬升,最后移动汽车,实现汽车的搬运。抱持式车辆搬运器由两个相同的搬运单元组成,分别负责抱持固定汽车的前后轮。单个搬运单元的转臂机构,如图1所示。为了清晰的表达转臂的结构,去掉了右边的横板部分。动力源通过对称机构使两端的横板可同时相对或相背移动。横板和转臂之间通过转臂轴铰连接。转臂上还有滚子轴,滚子轴上的滚子与滑槽形锁合。当动力源驱动时,可以实现四个转臂同步运动。由于结构对称,可取单侧转臂进行分析。现有的滑槽方案有采用135°斜槽式,90°直槽式,带圆角弧线等的低次曲线。设两段槽线夹角为β,按照有无圆角弧线过渡分类分析转臂加速度冲击性能。

图1 转臂机构示意图Fig.1 Schematic Diagram of Rotating Arm Mechanism
3 转臂冲击性能的分析
对转臂加速度冲击性能分析的核心是要研究其运动学特性。统一相关参数,如表1所示。

表1 相关参数Tab.1 Relevant Parameters
3.1 无圆角过渡的滑槽曲线
设定A1B1为转臂初始位置,A3B3为两槽线转折处的转臂位置,A2B2为运动中任意转臂位置,如图2所示。

图2 无圆角过渡槽型的转臂转动过程图Fig.2 The Process Chart of Rotating Arm of Groove without Transition Curve
用牵连速度法对任意位置A2B2进行转臂速度分析,如图3所示。则:
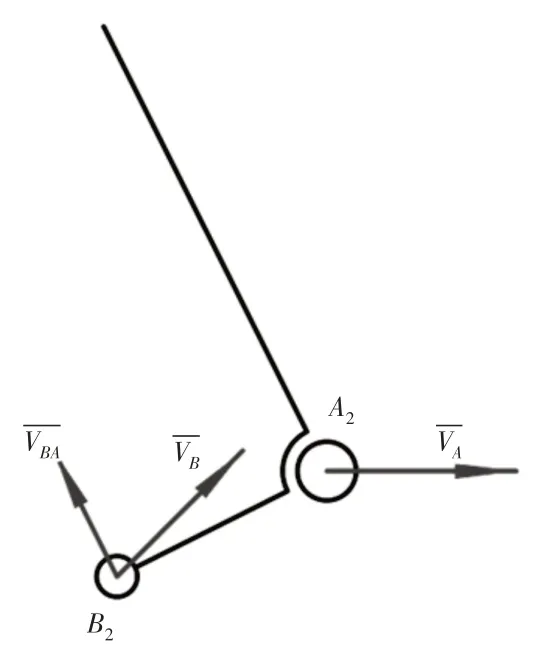
图3 转臂速度分析图Fig.3 Velocity Analysis of the Rotating Arm

式中:θ—转臂的角位移(rad);
t—时间(s);
L-AB杆长(mm);
β—两槽线所夹锐角(rad);
v—A点速度(mm/s)。
由式(1)可得转臂角速度ω(rad/s)和角加速度α(rad/s2)。
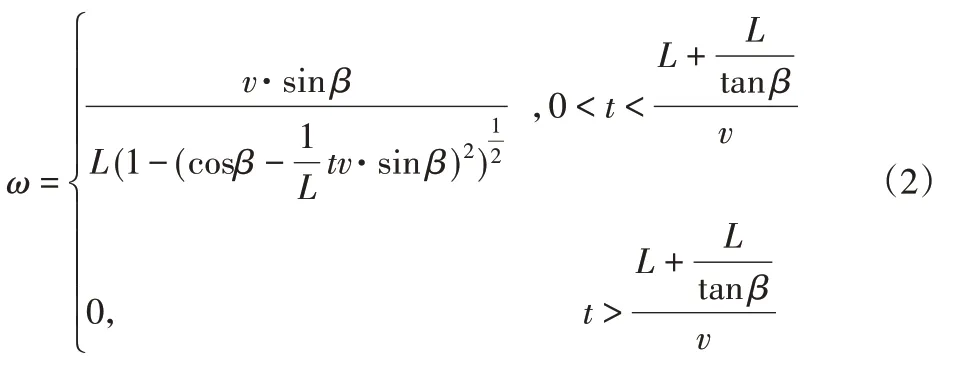
由式(2)、式(3)可知,转臂角速度ω在t=0处存在突变,故此点存在+∞的角加速度;转臂角速度ω在t=2L/v处存在突变,故此点存在-∞的角加速度,所以转臂在A1B1和A3B3处存在刚性冲击。
3.2 有圆角过渡的滑槽曲线
如图4所示,建立坐标系,其中,A1B1为转臂初始位置,B3为第一段槽线和圆弧段交点,B5为圆弧段与水平段槽线的交点。A2B2为第一段槽线上任意位置,A4B4为圆弧段任意位置。

图4 含圆角弧线过渡槽型的b点轨迹图Fig.4 Locus of B-Point Motion of Groove with Transition Curve
根据几何关系可得:

A2B2处的运动学分析与2.1中基本相同;A4B4进行转臂速度分析,如图5所示。

图5 圆弧段转臂速度分析图Fig.5 The Analysis of Arm Rotation Speed of Arc Curve Segment
可得:

式中:θ—转臂的角位移(rad);t—时间(s);L—AB杆长(mm);β—两槽线所夹锐角(rad);v—A点速度(mm/s);R—圆角弧线的半径(mm);φ—圆弧切线与x轴的夹角(rad)。
联立式(3)、式(4)可得转臂角位移:

式中:t2—B点到达B1点的时间(s);t3—B点到达B5点的时间(s);θ—转臂的角位移(rad);t—时间(s);L—AB杆长(mm);β—两槽线所夹锐角(rad);v—A点速度(mm/s);R—圆角弧线的半径(mm);φ—圆弧切线与x轴的夹角(rad)。
由式(5)对时间t求一阶导数和二阶导数,可得转臂速度与加速度方程。式子过于复杂,此处不一一展开。最后可知,转臂角速度ω在t=0s处存在突变,故此点存在-∞的角加速度,即此处存在刚性冲击。在t=t2s和t=t3s处,转臂角加速度α存在突变,故在这两个点存在柔性冲击。
4 高次滑槽曲线
采用高次曲线,令其在起始点与转折点处的角速度和角加速度曲线连续,则可以得到一种没有加速度冲击的高次滑槽曲线,如图6所示。
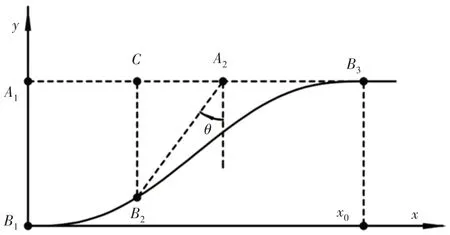
图6 高次滑槽曲线的单边转臂简图Fig.6 The Motion Diagram of the Rotating Arm of the High-Order Curvilinear Groove
根据几何关系得:

式中:C0,C1,……,Cn—高次曲线每一项的系数。

取中间任意位置A2B2进行分析,如图7所示。
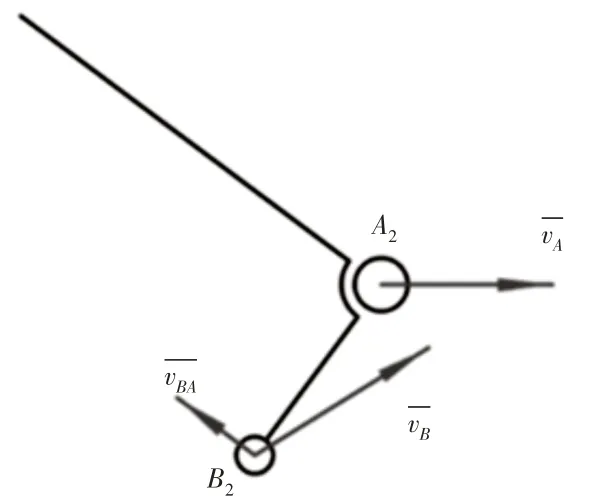
图7 高次曲线槽型的转臂速度分析图Fig.7 Analysis of the Speed of the Rotating Arm of the High Degree Curve Groove

式中:θ—转臂的角位移(rad);t—时间(s);L—AB杆长(mm);v—A点速度(mm/s);φ—曲线的切线与x轴的夹角(rad)。带入边界条件:

式中:ω—转臂的角速度(ran/s);α—转臂的角加速度(rad/s2);x0—高次曲线段长度;L—AB杆长(mm);v—A点速度(mm/s)。
联立式(10)-式(13)得无加速度冲击的轨道槽线方程:
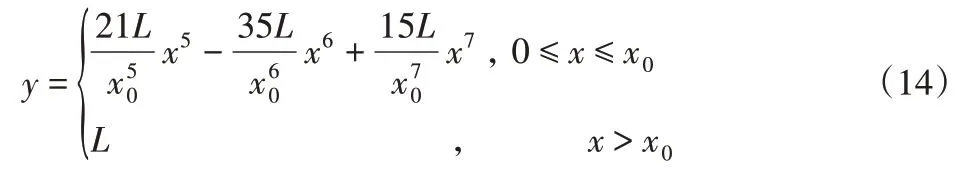
5 加速度图像分析
根据三种抱持式车辆搬运器轨道槽型曲线的角位移公式,代入表1中的已知参数,取β=45°和β=90°,分别以135°槽线和90°槽线为例,利用MATLAB软件获得相应的角加速度图像,如图8~图10所示。
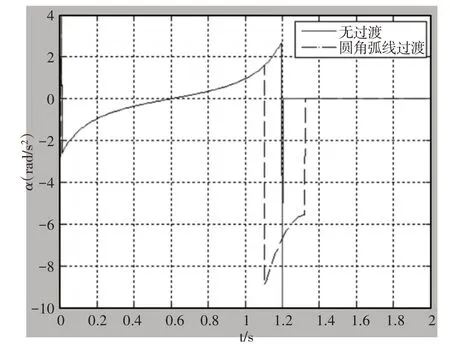
图8 135°斜槽式槽形的转臂角加速度曲线图Fig.8 Angular Acceleration Diagram of Rotating Arm of 135° Groove Angle

图9 90°直槽式槽形的转臂角加速度图Fig.9 Angular Acceleration Diagram of Rotating Arm of 90° Groove Angle

图10 高次曲线的转臂角加速度图Fig.10 Angular Acceleration Diagram of the Rotating Arm of the Groove Type of the High-Order Curve
对比无圆角过渡槽线和有圆角过渡槽线的抱持式车辆搬运器转臂的角加速度图像,图像显示,无圆角过渡槽线的搬运器转臂在展开的过程中具有两次刚性冲击,分别位于初始位置和槽线相交点。采用了圆角过渡的曲线结合高次滑槽曲线在初始位置具有一次刚性冲击,在两个槽线圆弧过渡点处存在两次柔性冲击。表明采用圆弧过渡有一定缓和冲击的作用,能将刚性冲击转化为柔性冲击。而采用了高次滑槽曲线的搬运器转臂在展开过程中,转臂的加速度曲线没有突变,不存在加速度冲击。
6 结论
(1)抱持式车辆搬运器的转臂槽线采用圆角弧线过渡比无圆角弧线过渡,具有一定的缓和冲击作用,可将一次刚性冲击转变成两次柔性冲击。(2)抱持式车辆搬运器的转臂槽线采用高次曲线,带入无冲击的边界条件求解,能够得到其转臂在展开过程中无加速度冲击所需的槽线方程。采用这种高次曲线槽型的转臂具有更长的使用寿命。(3)采用解析法获得转臂的加速度函数,可为其他车辆搬运器转臂机构的设计提供有效的参考方法。

