不均匀横流对传热管束全场管流致振动的影响

李先达，张 锴，熊珍琴,*，矫 明，王帅权，顾汉洋

(1.上海交通大学 机械与动力工程学院，上海 200240；2.上海核工程研究设计院有限公司，上海 200233)

蒸汽发生器是压水堆核电站中连接一、二回路的重要设备。蒸汽发生器的传热管一次侧为冷却剂，二次侧为气水混合物，存在流致振动致使其磨损失效的风险。传热管流致振动的机理主要有3种：湍流抖振、漩涡脱落和流弹失稳。流体速度低于流弹失稳临界速度时，漩涡脱落和湍流抖振是引发传热管磨损的主要原因[1]。而发生流弹失稳时，传热管会产生大幅度自激振动，造成传热管的快速磨损[2]。

针对蒸汽发生器传热管流致振动现象，国内外学者开展了大量研究。Weaver等[3]通过风洞实验研究了抗振条对全尺寸U型管束在均匀来流冲刷下的支撑作用。Chu等[4]通过实验研究了U型管束在气水两相均匀来流冲刷下的流弹不稳定性、阻尼比和水动力质量，并对流弹失稳临界速度经验关系式系数进行了修正。汪喆[5]对全尺寸多跨U型管三管束在底部两侧各一跨受横流冲刷下的振动响应进行了实验研究，研究表明，两侧流量不一致时对振动响应的影响仅出现在单侧的底部入口区。谭添才等[6]研究了不同空泡份额的均匀空气-水两相流对旋转三角形排列的单跨直管束失稳流速的影响，结果表明失稳流速随空泡份额的增大而增大。方夏鋆等[7]对支承板支承的4跨传热管束进行了中间2跨轴向分布的双向横流引起的流致振动实验研究，发现双向横流作用的传热管较单向横流更易失稳。张锴[8]针对传热管与支承板和抗振条之间间隙对传热管动态特性的影响进行了理论研究与模拟分析，结果表明传热管间隙导致传热管振动出现非线性效应，但对整体振动性能做简支处理仍是适用的。随着视觉测量技术的发展，视觉测振作为一种非接触测振手段开始在传热管振动研究中应用。Son等[9]探索了使用相机对传热管振动位移的可视化测量方法，分析评估了可视化测振的可行性，可视化测量实验获得的振动位移均方根与激光位移传感器测量结果相差1.3%。

上述文献调研显示，当前研究主要集中在均匀来流或轴向不均匀横流冲刷下传热管的流致振动现象，不均匀横流作用下的传热管束流致振动研究鲜有报道，迫切需要对不均匀横流下全管的振动响应规律开展研究。本文拟搭建28根传热管束组成的实验装置开展不均匀横流作用下的振动响应研究，并通过高速相机可视化拍摄获取传热管全管束振动响应规律。

1 实验方法

1.1 实验装置

本文传热管束实验段如图1所示，主要由模拟传热管、中间支承板、顶部支承板、流量调节板和外壳组成。模拟传热管束由28根圆管和10根半圆管组成，呈旋转正三角形排布。传热管直径D为17.5 mm，管壁厚度为1.1 mm，管间距P为25 mm。传热管竖直放置，底部焊接在外壳中。传热管在高度上设置中间支承板和顶部支承板两处支承，分为3跨，长度L1、L2、L3分别为900、900、72 mm。中间跨L2受到流体横向冲刷，其余两跨无横流冲刷。为形成不均匀横流，在第1排管束前160 mm处设置了1/3宽开口流量调节板。两处支承均为梅花孔形式，内切圆直径为17.84 mm、厚度为28 mm。为实现可视化观测，实验段壳体顶部采用有机玻璃盖。流致振动实验采用常温常压水为工质，实验段流量调节板前流道长10倍水力直径、管束后流道长5倍水力直径。为与1/3开口流量调节板形成的不均匀横流进行对比，本文还设置了一均匀开孔的流量调节板进行实验，两种流量调节板结构如图1c所示，均匀孔板的孔径为10 mm、孔间距为25 mm。

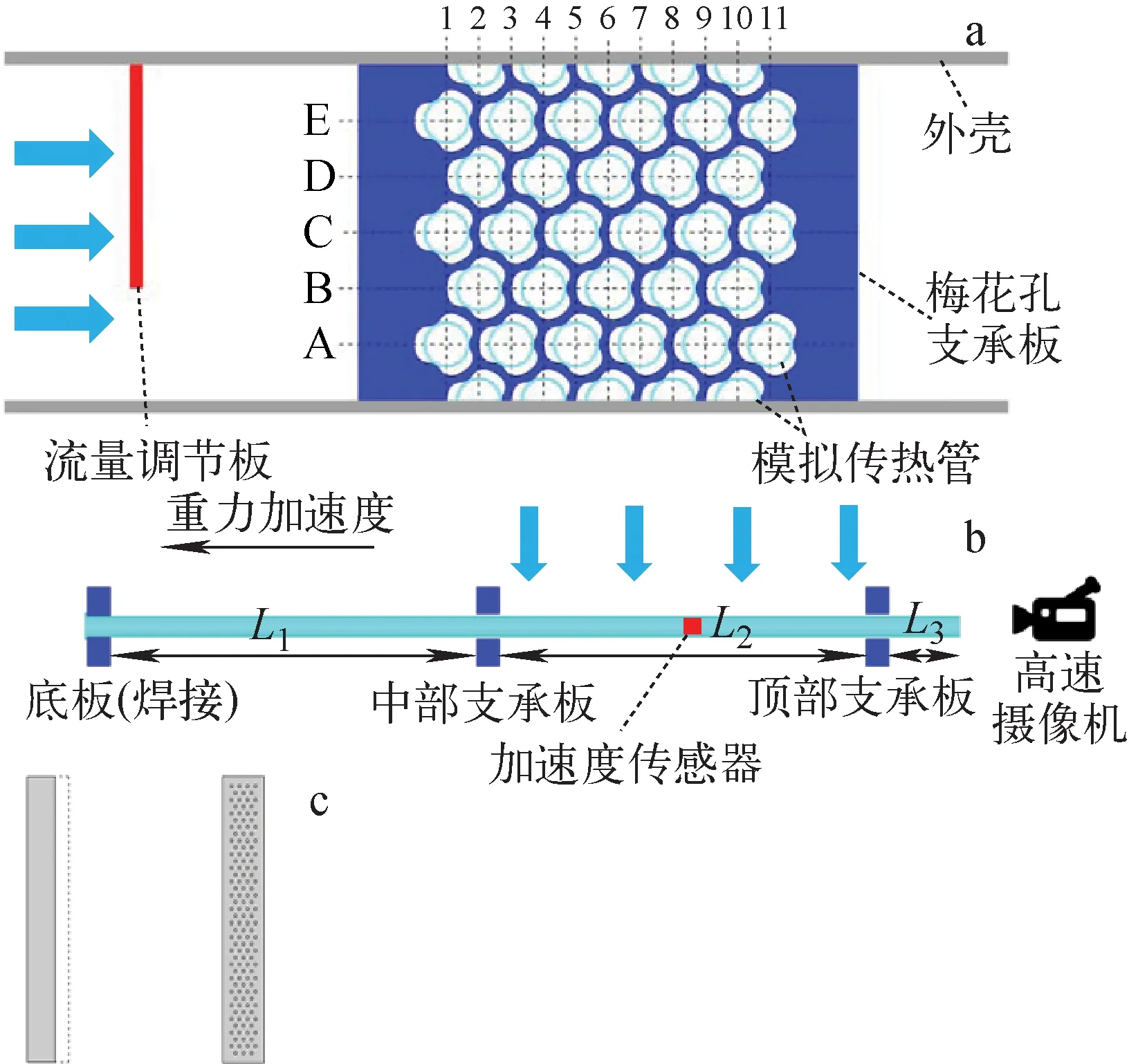
a——管束截面图；b——传热管支承结构；c——1/3开口与均匀孔流量调节板图1 实验装置示意图Fig.1 Schematic diagram of experimental device

1.2 测量方法

流致振动实验测量参数包括进入实验段流体流量、压力和传热管的振动响应。流体流量采用精度为0.5%的涡轮流量计测量，上游水压力由精度为0.1%的压力传感器测量。传热管的振动响应采用加速度传感器和可视化拍摄两种方式测量。加速度传感器(Endevco 65-10型三轴加速度传感器，测量范围0～500 g，精度±10 mV/g)布置在A-1传热管中间跨的跨中(图1b)。实验中加速度传感器的采集频率为10 240 Hz，每组工况采集120 s。为获得不均匀横流时全场各管的振动响应，使用Phantom高速相机从上往下拍摄传热管束顶部振动响应，像素为1 024×768，拍摄帧率为3 600 Hz。为提高精度，传热管顶部贴图2所示环形编码标志点，该编码为10位二进制编码，可标识每根传热管，并提高圆心捕获精度，实现传热管振动轨迹的获取。

a——编码标志点；b——相机拍摄的原始图像；c——透视变换后的图像图2 编码标志点设置Fig.2 Setting of coded reference point

1.3 数据处理方法

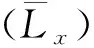
(1)

(2)

(3)

式中：i为图像帧序号；N为采集帧数。

可视化测量误差包括图像噪声、环境光照以及图像处理误差等，本实验以零流量下可视化测量的误差作为该组合误差。在入口流量为0时每隔5 min进行1次拍摄，共拍摄6次，并处理获得零流量传热管振动位移有效值，认为该值为可视化测量振动位移的误差。实验获得的振动位移列于表1。6次实验的传热管位移有效值在2.5～2.7 μm之间，最大振动位移有效值为管外径(D)的0.016%。本文用可视化测量拍摄平均管间流速在1.3 m/s以上工况的振动响应，最小振动平均位移为管外径的0.12%，测量相对误差小于14%，最大振动平均位移为管外径的1.5%，测量相对误差小于1.1%。可视化方法测量该流速区域的结果误差较小。

表1 误差测量实验结果Table 1 Result of error measurement

采用加速度传感器获得传热管跨中的加速度数据。对加速度频域进行2次积分再进行傅里叶逆变化获得传热管跨中振动位移，该方法详见文献[11]。

传热管受到的横流采用平均管间流速Up来表征，其计算公式如下：

(4)

式中：Q为入口体积流量；A为入口流道面积。

2 固有频率分析

传热管束中部与靠近顶部位置由梅花孔支承板支承，形成三跨结构，梅花孔与传热管同心时最小间隙为管外径的0.097%。传热管与支承板接触方式随振动强度而变化。横流速度较小时，传热管受到横流作用力较小，在摩擦力等共同作用下，存在依靠在中部或顶部支承板的现象，此时接近固支。当传热管支承处存在振动位移但又较小时，支承约束弱，近似无约束。当支承处振动位移较大时，传热管受到较强约束，此时接近简支。为此，将两处支承约束假设为无约束、简支与固支3种情况，使用有限元软件Abaqus对传热管建模分析获得固有频率。计算获得的前3阶模态固有频率列于表2。

表2 传热管固有频率模拟结果Table 2 Simulation result of natural frequency of heat exchanger tube

3 结果分析

3.1 失稳临界速度分析

传热管束在不均匀横流作用下的振动实验从平均管间流速0.42 m/s开始，流速逐渐增加，在管间流速为2.91 m/s时传热管剧烈振动，相互碰撞发出显著声响，发生失稳。图3为第1排正对来流传热管(A-1管)跨中和顶部的振动位移有效值。跨中由加速度传感器测量、顶部由高速相机可视化测量获得。在1/3开口流量调节板工况下，2处测量结果均在管间流速从2.8 m/s增大到2.91 m/s时位移有效值出现显著增加。其中，跨中的两个方向振动位移有效值分别从2.8%和6.0%上升到89%和198%；顶部则分别从0.32%和0.84%上升到1.2%和2.0%。图3同时给出了均匀孔来流结构时传热管的振动响应，在平均管间流速为3.18 m/s时发生流弹失稳。对比均匀孔来流结构可发现，1/3开口流量调节板更易发生流弹失稳，这是由于1/3开口流量调节板工况下局部流速更高。

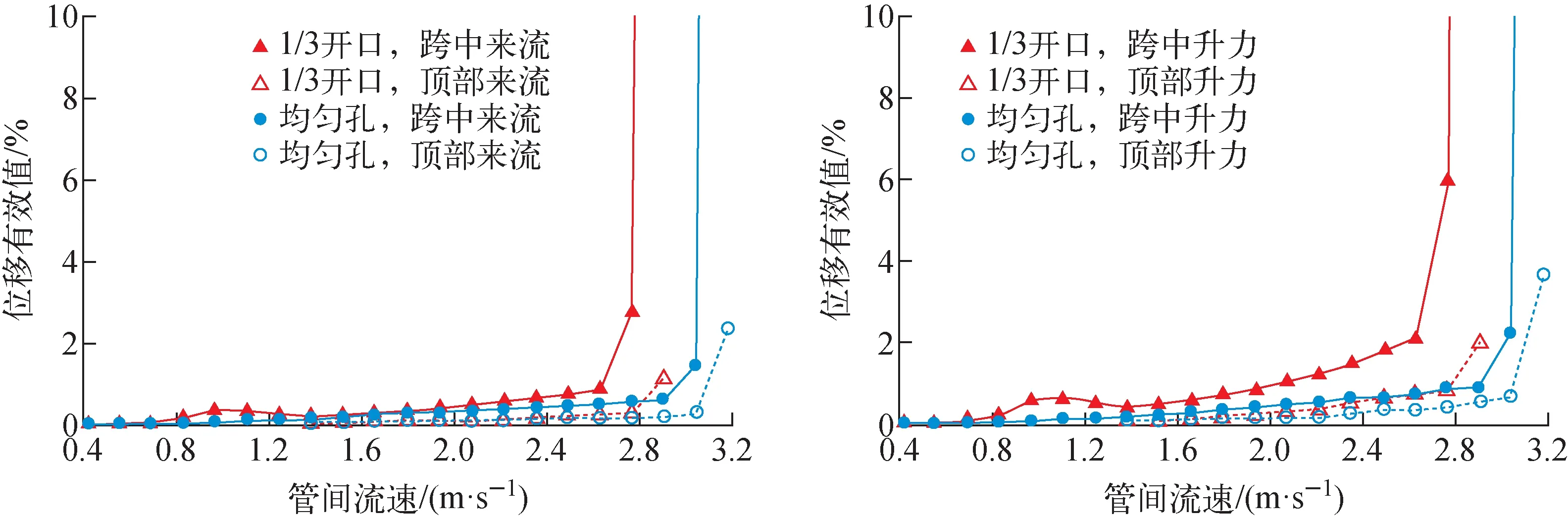
图3 第1排典型传热管振动位移有效值Fig.3 Displacement RMS of typical heat exchanger tube in first row

3.2 全管束振动响应分析

在不均匀横流作用下全场各管的局部来流速度存在显著差异，各管所受流体力和振动响应存在差异。为此，本文针对管间流速大于1.38 m/s的工况采用可视化方法测试全场各管顶部振动响应。实验发现，各管振动也存在显著的差异。图4为典型中等流速和失稳流速下全场各管顶部的振动轨迹，为便于观察，图中传热管振动位移放大5倍。从图4可看出，正对流量调节板开口的底部3列管束显著高于另外2列。失稳时顶部最大振动位移出现在第5排A-5管，该管周围的A-3、B-4、B-6管振动位移均较大。该区域管的振动轨迹主要方向会随平均管间流速而变化。当平均管间流速较小(2.08 m/s)时，升力方向振幅显著大于来流方向，此时A-1管略呈现最大振幅方向偏离升力方向的现象，最大振幅方向与来流方向夹角约为101°。该种偏离现象随着来流速度的增强出现区域扩大，在失稳工况时第2～5排传热管中更为显著。造成这种现象的原因是来流不均匀，该区域流场的主流方向不再是水平方向，而是与水平方向呈一定夹角。

图4 传热管束振动轨迹Fig.4 Vibration track of heat exchanger tube bundle

管束左上、左下、右上、右下和中间各处6根典型管的振动位移有效值与平均管间流速的关系示于图5。可见，振动位移最大值始终出现在管束中心偏下区域，A-5管的升力方向振动位移最大，B-4管次之。这是由于该区域管间流速较大，湍流作用力、旋涡脱落、管束中间的流体弹性力的作用均较强。振幅最小的区域发生在右上角，该区域远离流量调节板开口且距离入口最远，流速分布较均匀。结合传热管振动峰值频率的变化，可将传热管分为4个区域(标记为Ⅰ、Ⅱ、Ⅲ、Ⅳ)，如图6所示，图6中括号内数值分别为对应传热管来流方向和升力方向的位移频谱主峰值频率。

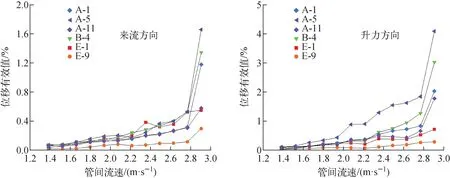
图5 全场典型传热管振动位移有效值与管间流速的关系Fig.5 Root-mean-square displacement of typical tube vs pitch velocity

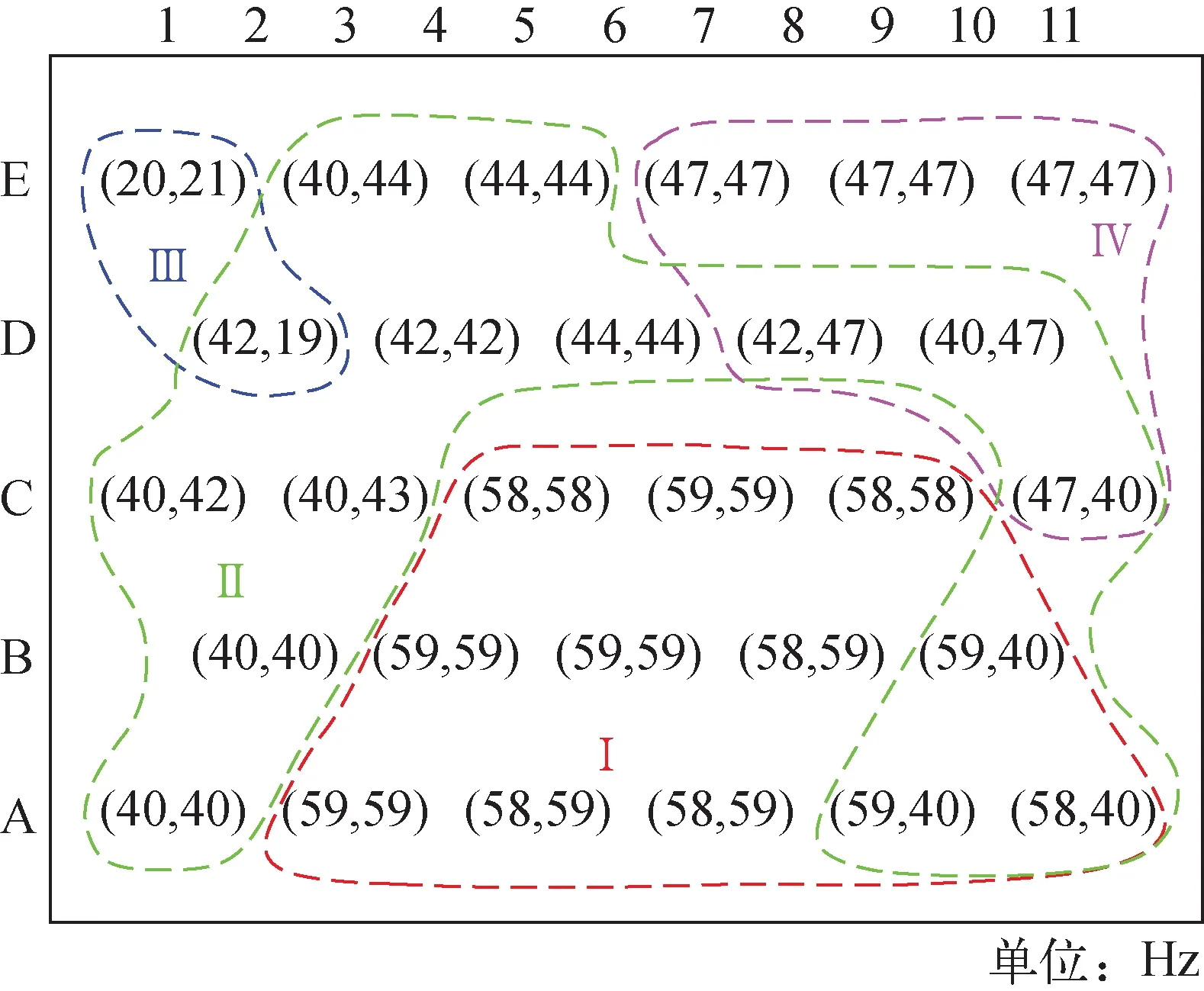
图6 传热管束位移峰值频率分布Fig.6 Peak frequency of displacement of tube bundle

区域Ⅰ为全场振动最强烈的区域，包括前述A-5、B-4管。由于振动剧烈，中间和顶部两处支承均有较好的约束，特别是发生失稳时。该区域峰值频率如图7a所示，失稳发生前，平均管间流速为2.8 m/s时，各管峰值频率在40～47 Hz区间，较分散。当平均管间流速增加至2.91 m/s时，振动幅值急剧增加，从图5能观察到该区域A-5和B-4传热管的振动位移有效值快速增加，此时峰值频率集中在58～59 Hz，发生了流弹失稳。该峰值频率与表2中结构6(中部固支、顶部简支)的1阶模态60.8 Hz相近。

区域Ⅱ紧邻区域Ⅰ，该区域发生管束失稳时振动位移增加较平缓。该区域峰值频率在40～44 Hz区间，如图7b所示，该频率接近于表2中结构4的1阶模态固有频率45.8 Hz。即该区域管束的约束模式接近于两处均为简支。

区域Ⅲ位于管束的左上角，主要是D-2管和E-1管，该区域管束受横流流速较小，同时受到被流量调节板遮挡的流道下游易形成的局部旋涡的影响。振动峰值频率为19～21 Hz，与结构1的2阶模态20.2 Hz接近，传热管两处支承约束均接近于无约束状态。

区域Ⅳ管束主要是位于右上角的E-7、E-9和E-11管等。该区域管束发生失稳时，振动峰值频率集中在47 Hz，与表2中结构3的2阶模态50.1 Hz接近。管顶部处于简支约束，中间处于无约束状态。

3.3 流弹失稳预测分析

工程上常采用经验关系式快速预测流弹失稳。为评估经验关系式预测不均匀横流工况流弹失稳的适用性，将实验结果与5种流弹失稳临界速度预测经典关系式进行对比，这5种经典关系式为Connors[12]、Gorman[13]、Weaver(1978)[14]、Chen[15]和Weaver(1981)[16]。其形式均如式(5)所示，常数b和C存在差异。

(5)

式中：ξ为阻尼比；m为传热管包含流体附加质量的等效单位长度质量，为0.76 kg/m；f为频率；ρ为流体密度。

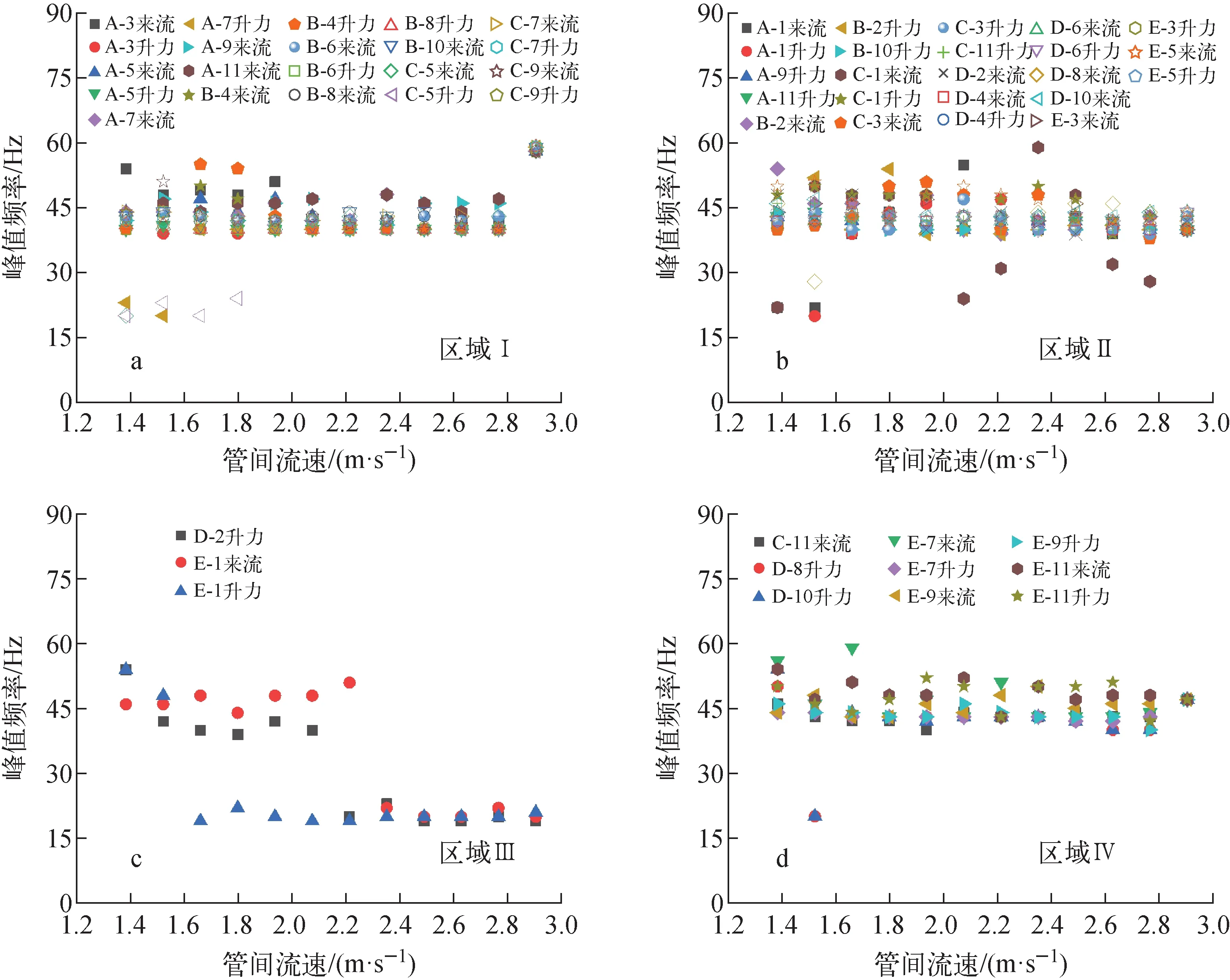
图7 传热管束位移峰值频率随管间流速的变化Fig.7 Displacement peak frequency of tube bundle vs pitch velocity

5种关系式预测结果列于表3。实验获得的不均匀横流下传热管束流弹失稳临界流速为2.91 m/s。与该数值相比，Connors关系式和Chen关系式预测结果偏保守，分别为1.45 m/s与2.19 m/s，两者预测结果分别较实验值低50.2%和24.7%。可见，适用于均匀来流的5种关系式均不能很好地预测本文实验的失稳临界流速。基于本文实验获得的不均匀横流下传热管束的失稳临界流速，对与实验结果最接近的Gorman关系式系数提出修正，修正后的系数C为5.8，计算得到的失稳临界流速为2.90 m/s。

表3 流弹失稳临界流速预测Table 3 Prediction of FEI critical velocity

4 结论

本文搭建了由28根圆管和10根半圆管组成的3跨长模拟传热管束可视化振动实验装置，通过高速相机视觉测量技术获得了受到经由1/3开口流量调节板产生不均匀横流冲刷时全场各管的振动响应规律。得到如下结论。

1) 实验获得了不均匀横流作用下传热管束流弹失稳临界流速，并与5种经典失稳临界流速预测关系式的预测结果进行了对比。其中Connors和Chen关系式是保守关系式，两者预测结果分别较实验值低50.2%和24.7%。

2) 在不均匀横流作用下传热管束较均匀孔来流更易发生流致振动，且呈现显著的区域性。失稳时28管束呈现4个区域振动特征。正对来流管束中心偏下区域的传热管振动位移最大，该区域为显著流弹失稳共振区域。其余3区有各自的振动峰值频率，且相邻区域存在过渡区。

3) 基于高速相机的振动视觉测量方法，获得了传热管全管束顶端的流致振动响应，在来流速度中等以上工况实现了较高质量的测量，流速最低工况误差最大，平均振动位移最大相对误差在14%以内。