螺旋管蒸汽发生器三维热工水力程序HeTAF开发

刘 凯，王明军，章 静，田文喜，秋穗正，苏光辉

(西安交通大学 核科学与技术学院，陕西 西安 710049)

蒸汽发生器是核动力系统一、二回路能量传递枢纽，作为核反应堆一回路压力边界，是一回路带放射性冷却剂与二回路工质的隔离屏障。蒸汽发生器结构庞杂，且涉及热工水力现象复杂多变，因此其运行可靠性对核电厂安全运行具有重要意义[1]。

螺旋管蒸汽发生器具有结构紧凑、换热效率高、抗膨胀热应力强等优势，在能源动力、石油化工等领域得到广泛应用。国内外学者针对管侧和壳侧流动换热特性开展了大量实验研究。Messa等[2]和Genic等[3]分别采用多个具有不同节距、螺升角等结构参数的螺旋管换热器实验段开展了冷热流体逆流换热实验，获得了壳侧对流换热系数关系式；Zhao等[4]在一定系统压力、质量流量和加热功率范围内开展了一系列螺旋管内两相流动沸腾实验，获得了阻力和换热系数关系式；Hwang等[5]进行了具有不同螺旋直径螺旋管内干涸特性实验研究，结果表明在低质量流量下，二次流对干涸点含气率影响较大；白博峰等[6]研究了螺旋管蒸汽发生器在同步启动过程中的流动和传热特性，瞬态单相湍流传热和临界热负荷规律与稳态有明显不同；毕勤成等[7]开展了高压下高温气冷堆蒸汽发生器螺旋管内两相流动实验，得到了螺旋管内两相摩擦阻力关系式。

近年来，计算流体力学(CFD)方法在核动力系统安全分析中得到广泛应用[8-11]。Zhao等[12-13]针对立式U型管蒸汽发生器开展了正常运行及传热管堵塞事故工况下全尺寸热工水力特性分析，获得了液相温度、空泡份额等一二次侧关键参数分布；Mu等[14]实现了对长期运行条件下蒸汽发生器沉积物分布的预测，并分析和评估了沉积物污垢热阻对蒸发器传热性能的影响；He等[15]基于OpenFOAM开发了适用于管壳式换热器的多孔介质方法求解器，结合MB-2蒸汽发生器基准题开展了模型验证，计算结果与实验数据符合较好。针对高温气冷堆(HTGR)螺旋管蒸汽发生器，Li等[16]模拟了管束间流体热搅混过程，获得了不同流量下贝克莱数(Pe)沿流动方向的变化规律；Ma等[17]采用一维程序分析了启动过程及非均匀加热条件下两相流动不稳定性；Olson等[18]采用二维多孔介质方法开展了稳态热工水力计算，并研究了流量变化、换热管位移和堵塞对温度分布的影响。目前以螺旋管蒸汽发生器整体为对象的相关研究较少，因此开发其全尺寸三维热工水力特性分析程序并开展设备级数值模拟，对于螺旋管蒸汽发生器设计优化及安全评价具有重要意义。

开源CFD平台OpenFOAM具有编程环境开放特性，便于进行数据接口创建、模型修改植入及求解器编写，更好地满足用户自主开发需求，已在航空航天、化工过程等领域得到广泛应用。本文采用多孔介质方法对具有复杂多层螺旋套管结构的换热组件区域进行简化，构建壳侧流动换热特性数学物理模型，并建立管侧水-水蒸气两相流动沸腾换热特性分析模型，采用网格-节点数据映射方法实现管壳两侧耦合传热计算，基于OpenFOAM平台开发适用于螺旋管蒸汽发生器的三维全尺寸热工水力特性分析程序HeTAF。

1 数学物理模型

螺旋管直流式蒸汽发生器多采用套筒式组件结构，由外套筒、中心筒及二者之间环形腔体内多层反向缠绕螺旋套管组成，如图1所示。管壳两侧工质逆向流动，换热组件壳侧单相高温工质自上而下冲刷螺旋管束，管侧单相过冷水在螺旋管内自下而上流动，与壳侧流体换热后发生相变，依次经过泡状流、弹状流、环状流和滴状流后转变为单相蒸汽，存在复杂的两相流动沸腾换热现象。

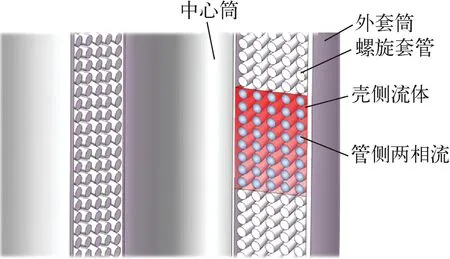
图1 换热组件几何结构示意图Fig.1 Schematic diagram of heat exchange assembly geometric structure

1.1 壳侧工质流动换热模型

本文基于多孔介质方法对换热组件内复杂螺旋管结构进行简化，建立了壳侧工质流动换热特性数学物理模型，其控制方程如下。

1) 质量守恒方程：

(1)

2) 动量守恒方程：

(2)

3) 能量守恒方程：

(3)

其中：下标s指壳侧流体相关参数；β为换热组件内壳侧流域孔隙率；ρ为密度；U为流速；p为压力；h为比焓；g为重力加速度；μ为动力黏性系数；α为热扩散系数；SM为由螺旋管束引入的阻力源项(忽略外套筒与中心筒的表面摩擦)；SE为壳侧工质被低温螺旋管壁冷却而引入的对流换热源项。

SM表达式为：

(4)

其中：L为流动方向长度；Af为单位体积内流通面积；fs为壳侧工质横掠螺旋管束摩擦阻力系数，由Idelchik关系式[19]计算；De为水力学直径，可由壳侧流通体积与润湿面积等效计算。

De表达式为：

(5)

fs表达式为：

(6)

其中：S1和S2分别为相邻螺旋管横向间距和纵向间距；do为螺旋管外径。

SE表达式为：

SE=-hs(Ts-Tw,o)At

(7)

其中：Tw,o为螺旋管外壁面温度；At为单位体积内螺旋管外壁面面积；hs为螺旋管表面对流换热系数，根据Zukauskas关系式[20]计算，其表达式为：

(8)

其中：Prw为定性温度取壁面温度的普朗特数；λ为热导率。

1.2 水-水蒸气两相流动沸腾换热模型

均相流模型将两相混合物流动视为具有特殊流动参数的均匀单相流动，不考虑相间相互作用，其假想物性由气液饱和状态参数加权平均获得，具有模型形式简易、可靠性强等优势。相关研究[21]表明，螺旋管中气液两相流动基本处于热力学平衡状态，且滑速比整体较小，均相流模型在螺旋管蒸汽发生器热工水力特性分析中的适用性和计算精度已得到广泛证明，因此本文采用均相流模型描述螺旋管内两相流动沸腾换热过程。由于管内流动Pe较大，对流作用占主导，因此忽略动量及能量扩散[22]，则控制方程如下。

1) 质量守恒方程：

(9)

2) 动量守恒方程：

(10)

3) 能量守恒方程：

(11)

其中：下标m指管侧均相流相关参数；Gm为质量流密度；qw,i为管内壁热流密度；Ci为螺旋管内截面周长；Ai为螺旋管内截面积；fm为摩擦阻力系数。

均相流物性参数通过下式求解：

(12)

(13)

ρm=αρg+(1-α)ρl

(14)

(15)

λm=xeλg+(1-xe)λl

(16)

其中：下标l和g分别指饱和水和饱和蒸汽的相关参数；xe为平衡态含气率。

在螺旋管换热器中，过冷水沿管侧流动与管壁换热并发生流动沸腾，随着空泡份额的上升，两相流型逐步转变，最终液相被完全蒸干，全部转变为单相过热蒸汽。本文在计算中根据换热机理，将管侧流动分为如下区域：单相水对流区、欠热沸腾区、饱和沸腾与强迫对流蒸发区、干涸缺液区和单相蒸汽对流区，各区域间换热机理转变的判断标准列于表1。

对于单相水和单相蒸汽对流区，选用广泛适用于管内流动换热的Schmidt关系式[24]，其表达式为：

Num=

(17)

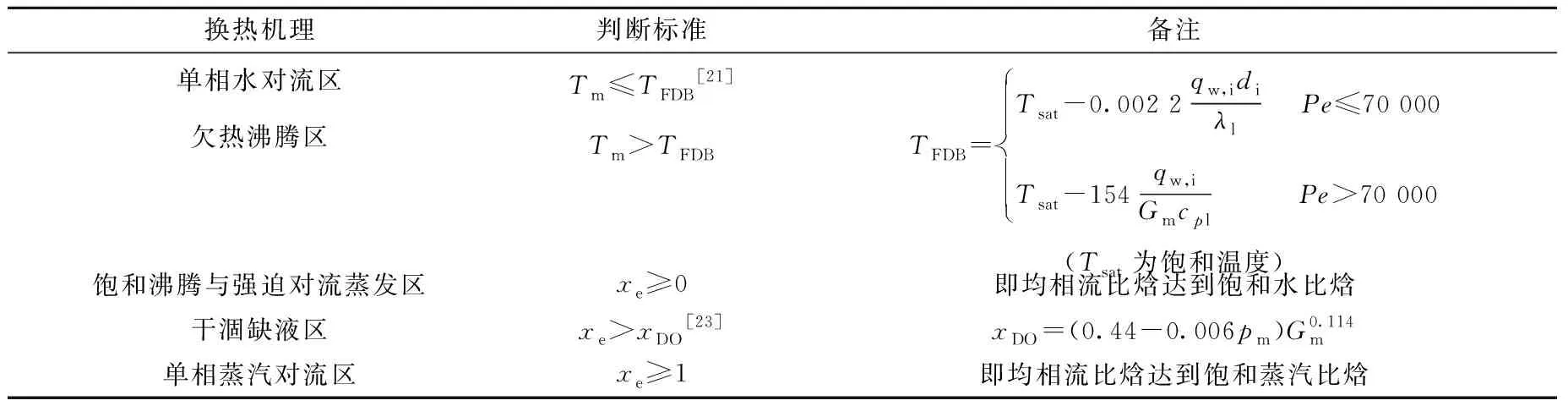
表1 管侧换热机理转变判断标准Table 1 Criterion for transition of tube side heat transfer mechanism

其中：di为螺旋管内径；Dc为平均螺旋直径；Nu、Re和Pr分别为管侧流体努塞尔数、雷诺数和普朗特数；常数Re1和Re2分别为22 000和150 000；Recr为临界雷诺数，本文采用Ito关系式[25]计算。

在饱和沸腾与强迫对流蒸发区，随着相变的进行，汽泡在主流聚集并形成高速流动的蒸汽核心。该区域换热系数采用Chen关系式[26]计算，其表达式为：

(18)

其中：cp为比热容；ΔTsat为饱和温度与当前温度差值；Δpsat为饱和压力与当前压力差值。

在欠热沸腾区，加热面产生汽泡跃离成核点后被主流冷凝，对该区域采用基于饱和沸腾关系式(式(17))修正后的Zhao关系式[27]计算，即：

(19)

对于干涸缺液区，近壁面液膜受加热蒸干及汽泡撕扯作用，逐渐减薄直至破坏，发生“干涸”。该区域换热系数采用Miropolskiy关系式[28]计算，其表达式为：

(20)

对于管内流体摩擦阻力系数，单相区内采用Ito关系式[25]计算：

(21)

其中，fs为层流摩擦阻力系数，其表达式为：

(22)

(23)

其中，Xtt为马蒂内利参数。

上述模型适用于0.001 1622 000的螺旋管内旺盛湍流流动，其中无量纲项di/Dc表征螺旋管内流体所受离心力的影响，具有较大螺旋直径的螺旋管内二次流作用强烈，形成涡旋冲刷壁面，增强主流与边界层间热质交换，使得管内流体换热能力和热平衡性增强，管侧热阻降低。螺升角增大会促使流体扰动增强，导致换热系数增大，但在螺旋管蒸汽发生器中螺旋管的螺升角通常较小，因此其影响不明显。

1.3 管壳两侧耦合换热模型

为实现三维多孔介质模型与一维均相流模型参数传递，开展了壳侧工质与管侧水-水蒸气两相流耦合换热求解，建立了三维计算网格与一维计算节点间数据映射关系，如图2所示。

图2 网格-节点数据映射示意图Fig.2 Schematic diagram of grid-node data mapping

沿组件高度方向将螺旋管束划分为N个离散节点作为均相流模型计算载体，则集总于各节点的螺旋管长度Ln、换热面积Sn(按外壁面面积计算)和管侧流体体积Vn可分别表示为：

(24)

Sn=πdoLn

(25)

(26)

其中：Nt为组件内螺旋管总数；Lt为单根螺旋管长度。

同样地，将壳侧流体域沿组件高度方向划分为N层，与离散节点逐个对应，则任一管侧节点P与其高度范围内壳侧流体域P′存在耦合换热关系。通过对区域P′内控制体网格进行积分，得到体积平均的壳侧氦气温度TP′和对流换热系数hP′，将其作为边界条件用于均相流模型计算，其表达式分别为：

(27)

(28)

其中：NP′为区域P′内控制体网格总数；Vc,i为控制体网格i的体积；hc,i和hl,i为控制体网格i中管侧工质温度和对流换热系数。

忽略螺旋管表面沉积污垢热阻，则两侧总换热系数可表示为：

(29)

其中，λw为螺旋管热导率。该节点处换热量可表示为：

Qn=qw,oSn=htotal(Ts-Tm)Sn

(30)

忽略螺旋管壁热惯性，则螺旋管外壁面温度为：

(31)

综上，管壳两侧耦合换热求解流程如下：1) 根据假设(或更新后)的对流换热源项求解壳侧工质控制方程，获得壳侧流场及温度场分布，进而求得螺旋管表面对流换热系数；2) 根据网格-节点数据映射关系，将壳侧流体域网格氦气温度和对流换热系数体积平均积分，并作为边界条件传递至管侧一维均相流模型对应节点中；3) 求解管侧水-水蒸气控制方程，获得管侧流场及温度场分布，并重新计算两相流物性、沸腾换热系数等流动换热相关参数；4) 将步骤3中更新的各节点的螺旋管外壁面温度传递至壳侧流体域网格，计算壳侧工质的对流换热源项并作为步骤1的初始条件。按上述步骤反复迭代直至得到收敛的计算结果。

基于开源CFD平台OpenFOAM中的有限体积类库建立壳侧工质流动换热模型，并植入水-水蒸气两相流动沸腾换热模型及相应热物性模型，通过网格-节点映射方法实现热工水力参数传递及管壳两侧耦合换热模型的求解，开发了适用于螺旋管蒸汽发生器的三维全尺寸热工水力特性分析程序HeTAF。

2 数值模拟与结果分析

2.1 螺旋管实验验证

基于意大利SIET热工水力实验室Santini[30]螺旋管两相流动沸腾换热实验进行HeTAF模型验证，实验装置及实验段如图3所示。通过旁路管线与泵下游控制阀调整实验段流量，并设置节流阀以抑制密度波流动不稳定性，实验段上游预热器用于调节进口过冷水温度。

该实验采用开放式回路设计，工质为去离子水。实验段为一根竖直布置的螺旋管，其主要几何参数列于表2。通过直流电源对前24 m

表2 实验段几何参数Table 2 Geometric parameter of test section

实验段进行均匀加热以使管内流体发生沸腾，剩余螺旋管为绝热段。在不同轴向位置测温点处沿螺旋管外围均匀布置多个K型热电偶测量螺旋管外壁温。

对系统压力6 MPa下具有不同质量流速G与热流密度q的各实验工况进行模拟，得到管内流体与壁面换热系数在实验段内的分布，为使计算结果与实验记录数据方式一致，将管长转化为平衡态含气率，其对比如图4所示，其中实验数据设置20%误差棒。

图4 换热系数随含气率变化的计算值与实验值Fig.4 Measured and calculated heat transfer coefficient variation with equilibrium quantity

由图4可见，除首个实验工况数据序列中个别数据点外，其他计算误差均在20%以内，3个实验工况下平均计算误差分别为10.1%、6.8%和6.5%，即在高质量流速和热流密度条件下预测精度更高。由此可见，本文所采用模型能有效预测螺旋管实验段中两相流动沸腾换热特性。

2.2 换热组件模拟

本文以高温气冷堆示范工程[31-32]中的螺旋管直流式蒸汽发生器(HCOTSG)为对象，利用开发的自主化螺旋管蒸汽发生器三维热工水力程序HeTAF开展数值模拟，高温堆HCOTSG结构参数列于表3。

表3 HCOTSG几何参数Table 3 Geometric parameter of HCOTSG

针对螺旋管蒸汽发生器中单个换热组件开展两侧热工水力特性耦合分析，每个换热单元有5层，共35根螺旋换热管，从里向外每层螺旋管根数依次为5、6、7、8、9，相邻两层缠绕方向相反。各层螺旋管间螺升角和螺距不同，使得换热组件内所有螺旋管管长基本保持一致。研究[33-34]表明，在螺旋管蒸汽发生器实际工况下，热工水力特性对螺旋直径小幅变化不敏感，因此在模拟中采用平均螺旋直径430 mm作为特征螺旋直径求解相关参数，即采用特征管表征不同层螺旋管。沿组件高度方向划分150个计算节点，两侧相关参数列于表4。

表4 管壳两侧流动相关参数Table 4 Parameter of shell side and tube side fluid

模拟时计算域上下边界分别为氦气进出口边界，忽略换热组件对外辐射散热等其他热损耗，外套筒内壁面及中心筒外壁面设置为绝热壁面边界。氦气、单相过冷水及过热蒸汽热物性则由根据组件运行范围内多个温度下物性点拟合而成的多项式计算得到，处于两相区的汽液两相混合物的热物性则由对应工况下饱和水及饱和蒸汽热物性加权获得，如1.2节所述。壳侧三维计算网格和管侧一维计算节点上物理场和相关参数分别按热氦气和过冷水进口温度及流量初始化。管侧和壳侧流体及管外壁面温度沿组件高度方向分布计算结果如图5、6所示。

图5 管侧和壳侧流体及管外壁面温度沿组件高度方向的分布Fig.5 Distribution of tube side fluid, shell side fluid and tube outer wall temperature along height direction

图6 组件中管侧和壳侧流体温度分布Fig.6 Distribution of tube side and shell side fluid temperature in assembly

由图5可见，管侧流体存在单相水区、两相区、单相蒸汽区等3区分布，在螺旋管长约35 m处(对应组件高度约5 m处)发生饱和沸腾，呈明显温度平台，如图6a所示，在螺旋管长约52 m处(对应组件高度约7.4 m处)液相全部蒸干，管侧流体变为单相过热蒸汽，两相区长度约为17 m。相应地，壳侧氦气温度在组件上部冷却速度较快，而由于两侧换热能力下降，在组件下部温度减小趋势放缓，如图6b所示。可见，本文模型计算获得的两侧流体温度变化趋势与实际物理过程较符合。壳侧氦气和管侧蒸汽出口温度计算误差列于表5，两侧换热量计算值相比设计值略低。

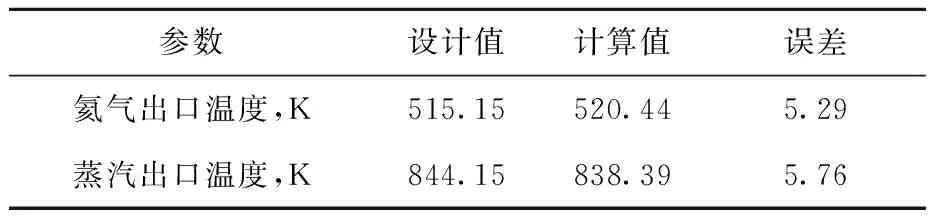
表5 组件出口温度计算误差Table 5 Calculation error of assembly outlet temperature

组件内壳侧及管侧流体换热系数、空泡份额和含气率沿螺旋管长度方向的分布如图7、8所示。在沸腾起始点前，管侧单相水与加热管壁对流换热；在进入两相区后，管侧流体沿螺旋管流动过程中相变逐渐剧烈，其换热机理随组件高度的增加而不断变化，依次经历欠热沸腾、饱和沸腾、强迫对流蒸发换热，管侧换热系数快速升高，最大值约为6.21×104W/(m2·K)。壳侧为氦气横掠螺旋管束的单相对流换热，换热系数相较于管侧在整个计算域内变化不大，其平均值约为2 383.57 W/(m2·K)。

图7 壳侧及管侧换热系数、空泡份额和含气率沿螺旋管长分布Fig.7 Distribution of tube side heat transfer coefficient,void fraction and equilibrium quantity along tube length

图8 组件中管侧换热系数和空泡份额分布Fig.8 Distribution of tube side heat transfer coefficient and fluid void fraction in assembly

由于空泡份额不断升高，导致两相流型改变，最终环状流液膜被破坏，壁面与气相直接接触并进入干涸缺液区，管侧换热系数骤降至2.5×104W/(m2·K)；最终液相完全蒸干，受热物性变化影响，单相蒸汽区中管侧换热系数有所下降，但由于蒸汽与管内壁面之间温差较大，换热功率仍高于单相水对流换热区。空泡份额在两相区前段上升较快，在后半段则趋于缓慢。

3 结论

本文基于多孔介质方法对换热组件内复杂螺旋管结构进行简化，建立了壳侧工质流动换热特性分析模型，针对管侧两相流动沸腾换热过程建立了水-水蒸气均相流模型，根据换热组件的空间对应关系，采用网格-节点数据映射方法进行模型间数据传递，实现了管壳两侧耦合传热计算，开发了适用于螺旋管蒸汽发生器的三维全尺寸热工水力特性分析程序HeTAF。基于螺旋管两相流动沸腾换热实验开展了模型验证；对高温气冷堆示范工程中螺旋管直流式蒸汽发生器的单个换热组件开展了两侧热工水力特性耦合模拟，结果表明：计算得到的氦气和蒸汽出口温度与设计值符合较好，绝对误差分别为5.29 K和5.76 K，表明本文所建立模型能有效预测换热组件内管壳两侧耦合流动换热特性。

未来将以单换热组件模拟策略为基础，对螺旋管蒸汽发生器开展全尺寸热工水力特性耦合分析，并针对HeTAF程序持续开展模型验证完善和应用范围推广等研究。