基于高维多目标候鸟优化算法的柔性作业车间调度

王秋莲 段星皓

南昌大学经济管理学院，南昌，330031

0 引言

柔性作业车间调度问题(flexible job shop scheduling problem，FJSP)是指在一定的约束条件下，同时确定工件加工机器和加工顺序，以达到理想的调度目标[1]。FJSP是NP-hard问题，大规模的FJSP很难通过数学规划方法、拉格朗日松弛法等精确方法求得理论解，因此更多的研究采用启发式算法对FJSP进行求解。如何改进启发式算法使得其收敛性、稳定性达到更优是当前研究的热点。

FJSP根据调度目标的数量分为单目标FJSP和多目标FJSP(multi-objective FJSP，MOFJSP)。其中，MOFJSP可进一步细分为低维(调度目标不超过3个)MOFJSP和高维MOFJSP。目前，大部分学者主要对低维MOFJSP进行研究，如孙丽珍等[2]以最小化最大完工时间、机器负载的均方差为目标，设计了一种改进解码方法和初始化规则的遗传算法；孟冠军等[3]提出一种混合人工蜂群算法求解以最大完工时间、最大机器负荷和机器总负荷为目标的低维MOFJSP。实际生产中，制造企业不仅需要考虑上述目标，还需要考虑能源消耗。李进宇等[4]研究了基于递归分析和图像处理技术的混流车间能耗。李明等[5]提出一种新型帝国竞争算法来求解以最小化完工时间、最大拖期、最大机器负荷和总能耗为目标的高维MOFJSP，但该方法对高维多目标解集个体的选择压力不足，可能导致算法的过早收敛。黄夏宝等[6]提出一种改进的NSGAⅢ算法，引入基于参考点的小生境选择机制来提高算法的多样性，求解以最小化最大完工时间、机器总负荷、最大机器负荷和机器能耗为目标的高维MOFJSP，但该算法的局部搜索能力还有待提高。由此可见，考虑能耗目标的高维MOFJSP研究是当前车间调度问题研究的热点及难点，但处于起步阶段[7]。

候鸟优化(migrating birds optimization，MBO)算法[8]可用于求解二次分配问题，且所得的最终结果优于遗传算法、模拟退火算法等常用算法。QUAN等[9]将MBO算法用于求解混合流水车间的调度问题；任彩乐等[10]提出两阶段解码方法及4种邻域结构的改进MBO算法，求解混合流水车间调度问题。此外，有学者通过MBO算法来求解FJSP，如姚妮[11]以最小化最大完工时间为目标，结合MBO算法和变邻域搜索策略来提高算法局部搜索能力；刘雪红等[12]设计一种改进的MBO算法，引入精英分批策略和可行邻域结构策略来解决以最小化最大完工时间和最大批次数目为目标的低维MOFJSP。

尽管这些学者证明MBO算法对FJSP能获得高质量解集，但用MBO算法进行高维MOFJSP的研究较少，因此本文建立一种以最小化完工时间、机器总负荷、延期时间、生产总能耗为优化目标的MOFJSP模型，在改进MBO算法的基础上，引入Pareto思想和基于参考点的选择算子，设计了一种高维多目标候鸟优化(multi-objective migrating birds optimization，MOMBO)算法，通过2种选择算子给予鸟群选择压力，以提高鸟群的多样性和收敛性，并基于属性层次模型和灰色关联度分析法的组合权重决策选择最优解。最后通过算例和实验验证算法的有效性。

1 高维多目标柔性作业车间调度模型

FJSP可以描述为：工件集J={J1，J2，…，Jn}中的n个工件在机器集M={M1，M2，…，Mm}中的m台机器上加工，其中，第i个工件Ji有ei个工序。MOFJSP主要需要解决两类子问题：机器选择和工序排序，其中，机器选择是指从可选机器集Mij(i∈[1，n]，j∈[1，ei])中选择一个机器完成工序Oij，工序排序是确定每个机器的加工顺序。

工件加工过程中，有以下假设：①所有机器在0时刻均可开始加工工件，所有工件在0时刻均被释放；②每台机器一次只能完成一道工序，每道工序在同一时刻只能由一台机器完成；③工件的加工需严格按照工序依次完成；④加工一旦开始就不能中止，直到完成；⑤机器完成最后一道加工就停止运行；⑥加工过程中，工件的转移时间忽略不计。

本文提出的多目标柔性作业车间调度模型的调度目标的具体描述如下：

(1)最大完工时间。最大完工时间是指所有工件加工完成的时间，即最后一个工件加工的完工时间，其计算公式为

f1=max(Ci|i=1，2，…，n)

(1)

式中，Ci为工件i最后一道工序的完工时间。

(2)总拖期。客户和企业会约定产品的交货期，交货时间超过交货期，企业会损失信誉并被罚款。总拖期可以反映企业的信誉情况，其计算公式为

(2)

式中，Di为工件i的交货期。

(3)机器总负荷。机器总负荷指所有加工机器的负荷总和，可以反映企业资源的利用效率，其计算公式为

(3)

式中，tijk为工序Oij在机器k上的加工时间；xijk为0-1变量，xijk=1表示工序Oij在机器k上加工，xijk=0表示Oij不在机器k上加工。

(4)总能耗。总能耗主要包括车间固定能耗、机器空载能耗、机器加工能耗，其计算公式为

(4)

(5)

(6)

Eg=Pgmax(Ci|i=1，2，…，n)

(7)

2 高维多目标候鸟优化算法

候鸟在飞行过程中会自然排成V字形队列，这是因为领飞鸟通过翅膀扇动形成一股气流，气流向后方流动从而加大后方压力，跟飞鸟利用压力差飞行得更加轻松。MBO算法模仿候鸟的迁徙过程，将表现最优的可行解作为领飞鸟，将其他可行解作为跟飞鸟。MBO算法主要分为鸟群初始化、领飞鸟进化、跟飞鸟进化和替换领飞鸟四个阶段。本文在此基础上，引入基于Pareto支配和基于参考点的选择算子，对鸟群初始化、飞鸟进化阶段进行改进，提出一种高维多目标候鸟优化算法，该算法流程如图1所示。

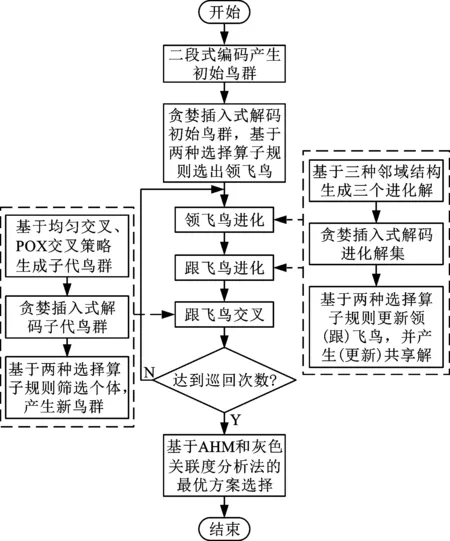
图1 高维多目标候鸟优化算法流程图

2.1 基于Pareto支配和参考点的选择规则

本文引入基于Pareto支配的选择算子和基于参考点的选择算子来增强对Pareto前沿面的选择压力，进而对解进行筛选和替换。

2.1.1基于Pareto支配的选择算子

Pareto支配的定义为：对于解p和q，当且仅当解p的所有目标值都不大于解q的目标值且至少存在一个目标值小于解q的目标值，则称p支配q(pq)。

定义si为鸟群中被个体i支配的个体集合，zi为鸟群中支配个体i的个体数量。

基于上述定义，提出一种快速非支配排序算法，具体步骤如下：

(1)将种群中不被其他个体支配的个体标记为第1级非支配前端F1；

(2)F1中的个体p支配的个体集合为sp，对于sp中的个体q，将支配q的个体数zq减1即zq←zq-1后，若zq=0即不存在可以支配q的其他个体，则将q保存至集合Q中。对F1的每个支配个体集合中的全部个体执行上述操作后，将最终得到的集合Q作为鸟群的第2级非支配前端F2；

(3)遍历F2中的个体，参照步骤(2)中的操作，找到第3级非支配前端F3。以此类推，直到种群中的每一个个体都分配到对应的非支配前端等级。

通过基于Pareto思想的快速非支配排序算法将鸟群分为不同等级，等级越低说明该个体越优。

2.1.2基于参考点的选择算子

基于参考点的选择算子首先在目标空间内采用单层参考点生成法[13]得到均匀分布的多个参考点，即将A个目标均匀划分成H份，然后根据参考点依附的个体数量选择较优个体，具体流程如下：

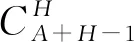
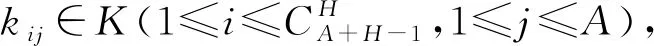
(8)

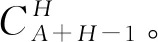
然后通过下式归一化鸟群个体的目标值：

(9)

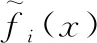
归一化鸟群个体的目标值后，此时理想点变为原点，然后将理想点与各参考点的连线作为参考线，计算归一化后的目标点与所有参考线的距离，选择最近的参考线作为个体依附对象；

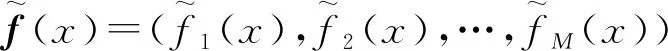
(10)

最后依次遍历鸟群个体，统计每个参考点的依附个体数量即该参考点的小生境数。在MOMBO算法鸟群进化操作时，对于同一级非支配前端中的个体集合，优先选择小生境数更少的个体，保证算法的多样性。

2.2 多目标候鸟优化算法的主要步骤

2.2.1编码

运用MOMBO算法求解MOFJSP时首先要解决编码问题，即将FJSP的潜在解转换至可被MOMBO算法搜索的空间中。本算法采用二段式编码规则[14]，将解分为机器选择(machine selection，MS)和工序排序(operation sequence，OS)两部分。MS按工件的工序顺序依次排列，每个位置的数值为该道工序选择的加工机器号；OS中，每个位置的数值为工件号，从左往右遍历OS，同一工件号出现第j次数表示对应工件的第j道工序。MS和OS如图2所示。

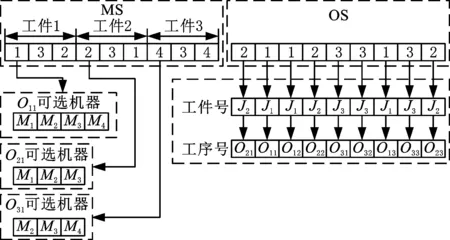
图2 二段式编码示意图

2.2.2解码

解码则是将解空间转换为问题空间。本算法采用贪婪插入式解码法[15]，以保证每道工序在所选加工机器上尽可能早地开始，对于前插的工序，它在OS上的位置也要相应调整。

2.2.3鸟群初始化

初始化是车间调度问题的一个重要步骤，它生成解集的好坏对算法的收敛性和多样性有很大的影响。为保证初始解的质量和多样性，本文分别对机器选择和工序排序采用多种初始化规则。

2.2.3.1 MS初始化规则

(1)改进的全局选择规则[16]。设定一个初始值为0的机器负荷数组，从工件集合中随机选择一个工件，从该工件的工序中随机选择一个工序，将该工序的可选机器加工时间与机器负荷数组的已有负荷相加，得到临时机器负荷数组。从临时机器负荷数组中选择临时负荷最小的机器作为该工序的加工机器；若临时负荷最小的机器不只一个，则选择加工时间最短的机器作为该工序的加工机器；更新机器负荷数组。当前工件的所有工序选择完加工机器后，随机选择下一个工件，依次类推，直到所有工件的工序都选择完机器。

(2)改进的局部选择规则[16]。设定一个初始值为0的机器负荷数组，从工件集合中依次选择一个工件，从该工件的工序集合中随机选择一个工序，将该工序的可选机器加工时间与机器负荷数组的已有负荷进行相加，得到临时机器负荷数组。从临时机器负荷数组中选择临时负荷最小的机器作为该工序的加工机器；若临时负荷最小的机器不只一个，则选择加工时间最短的机器作为该工序的加工机器；更新机器负荷数组。当前工件的所有工序选择完加工机器后，将机器负荷数组重新置0，选择下一个工件，依次类推，直到所有工件的工序都选择完机器。

(3)随机选择。在加工工序的可选机器中随机选择一台机器进行加工。

2.2.3.2 OS初始化规则

(1)剩余负荷最大规则[17]。将工件按剩余工序加工时间总和进行降序排列，优先加工剩余加工时间长的工件。

(2)最短加工时间规则[18]。将工序按照加工时间升序排列，优先完成加工时间短的工序。

(3)随机选择。随机选择工序进行加工。

参考文献[16，19]，首先按照鸟总数(即个体总数)4∶4∶2的比例，分别通过改进的全局选择规则、改进的局部选择规则和随机选择规则生成初始鸟群的MS，再按照上述比例生成初始鸟群的OS。

初始化之后，按如下步骤将鸟群分为领飞鸟和左右跟飞鸟群：首先根据基于Pareto支配的选择算子进行非支配排序，找到初始种群中的非支配解集；然后通过基于参考点的选择算子，选择小生境数最小的非支配解作为领飞鸟，若小生境数最小的非支配解有多个，则随机选择一个作为领飞鸟，并将剩下个体按非支配等级均匀分为左右跟飞鸟群。

2.2.4鸟群进化

首先定义三种邻域结构：

N1：随机产生i(i=2，3，4)个变异工序。将i个工序顺序重新排列组合，然后计算不同排列组合的目标值，通过上文中的两种选择算子选择其中最好的新解作为邻域解。

N2：基于工序变异，交换两个不同工件的任意工序位置。

N3：基于机器变异，随机选择两个变异工件，并在这两个变异工件上分别随机选择一道工序，在不考虑原加工机器的情况下，重新选择这两道工序加工时间最短的机器。

基于上述3种邻域结构，增加鸟群个体的局部寻优能力，鸟群进化具体步骤如下。

2.2.4.1 领飞鸟进化

按上述3种邻域结构产生领飞鸟的3个邻域解后，将领飞鸟与3个邻域解合并作为进化解集，接着从该进化解集中选择1个个体作为新的领飞鸟，具体的选择规则如下：①若邻域解支配领飞鸟，则替换领飞鸟；②若领飞鸟支配邻域解，则不替换；③若领飞鸟与邻域解互不支配，则进行领飞鸟选择，具体的领飞鸟选择操作如下。

首先将原鸟群中的进化个体剔除，计算剔除进化个体后的鸟群的小生境数；然后找出具有最小小生境数的参考点集J，遍历J中的每个参考点。假设Ja是J中的一个参考点，判断进化解集(包括进化个体、进化个体的邻域解)的非支配解集中是否有个体依附于参考点Ja，若进化解集的非支配解集中没有个体依附于参考点Ja，则将参考点Ja的小生境数ρa设为无穷大。若进化解集的非支配解集中有个体依附于参考点Ja，则进一步判断ρa是否为0，若ρa为0，则从进化解集的非支配解集中依附Ja的个体中将与参考点Ja对应参考线距离最短的个体作为新的领飞鸟加入鸟群；若ρa不为0，则在进化解集的非支配解集中随机选择1个依附该参考点的个体作为新的领飞鸟加入鸟群。进化过程中选择领飞鸟的流程如图3所示。

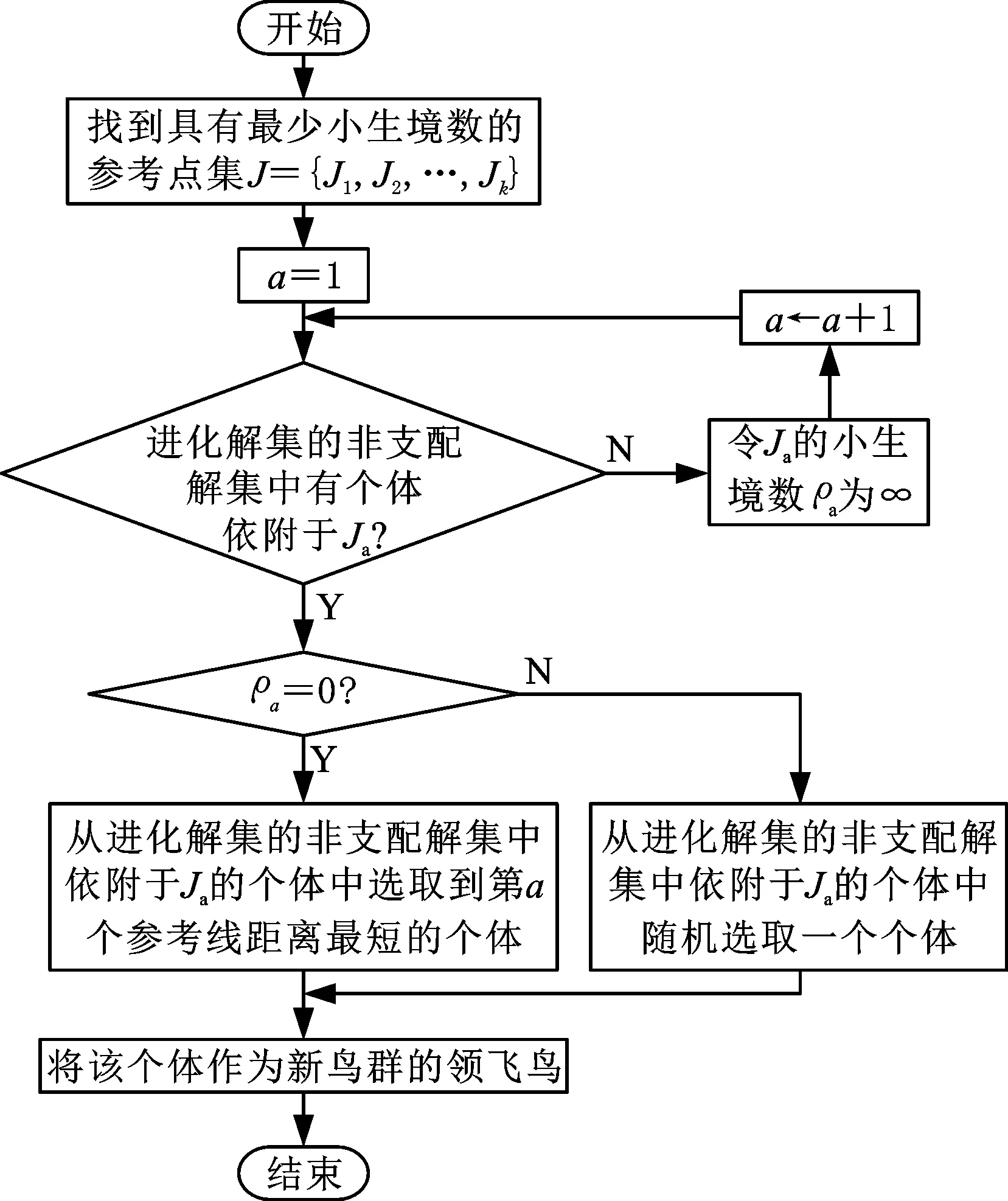
图3 进化过程中基于参考点的选择算子流程图

更新完领飞鸟之后，选择一个次优解作为第一个跟飞鸟的共享解，以增强跟飞鸟群的寻优能力。次优解的选择过程如下：判断进化解集中剩余个体的非支配等级，选择非支配等级最低的个体作为次优解；若非支配等级最低的个体数大于1，则比较其依附参考点在鸟群中的小生境数，优先选择小生境数更小的个体，若小生境数相同，则随机选择一个体作为次优解。

2.2.4.2 跟飞鸟进化

跟飞鸟进化包括对左右跟飞鸟群的进化，即首先将领飞鸟进化解集中的次优解作为左右跟飞鸟群中第一只跟飞鸟的共享解，将共享解与生成的3个邻域解组成该跟飞鸟的进化解集。然后，选择进化解集中的最优解作为新的跟飞鸟，同时将进化解集中的次优解作为下一只跟飞鸟的共享解，替换跟飞鸟和选择次优解规则与上文中领飞鸟的进化过程相同。按上述步骤依次遍历所有跟飞鸟，完成跟飞鸟的进化。

2.2.5跟飞鸟交叉

每次对左右跟飞鸟群执行完进化操作后，从左右跟飞鸟群中随机选择Cr(Cr为交叉个数)对个体，并对每对个体依次进行交叉操作。

MS、OS的交叉操作分别采用均匀交叉策略和POX(precedence operation crossover)交叉策略[15]。MS的均匀交叉策略是：随机产生一个长度为工序总数的0、1数组，交换父代数字1对应位的机器号，产生2个新的子代。OS的POX交叉策略是：首先将工件随机地分为子集合J1和J2；然后将父代1中J1部分的工件号复制到子代1对应位置，将父代2中J2部分的工件号复制到子代2中对应位置；最后将父代2中J2部分的工件号按顺序依次填入子代1中的剩余位，将父代1中J1部分的工件号按顺序依次填入子代2中的剩余位。MS交叉如图4所示，OS交叉如图5所示。

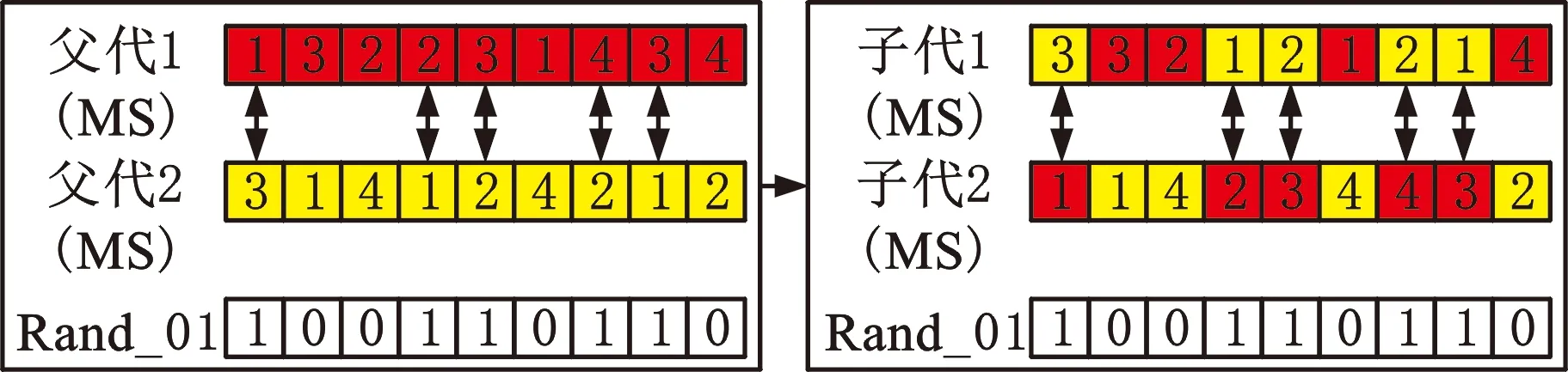
图4 MS均匀交叉图

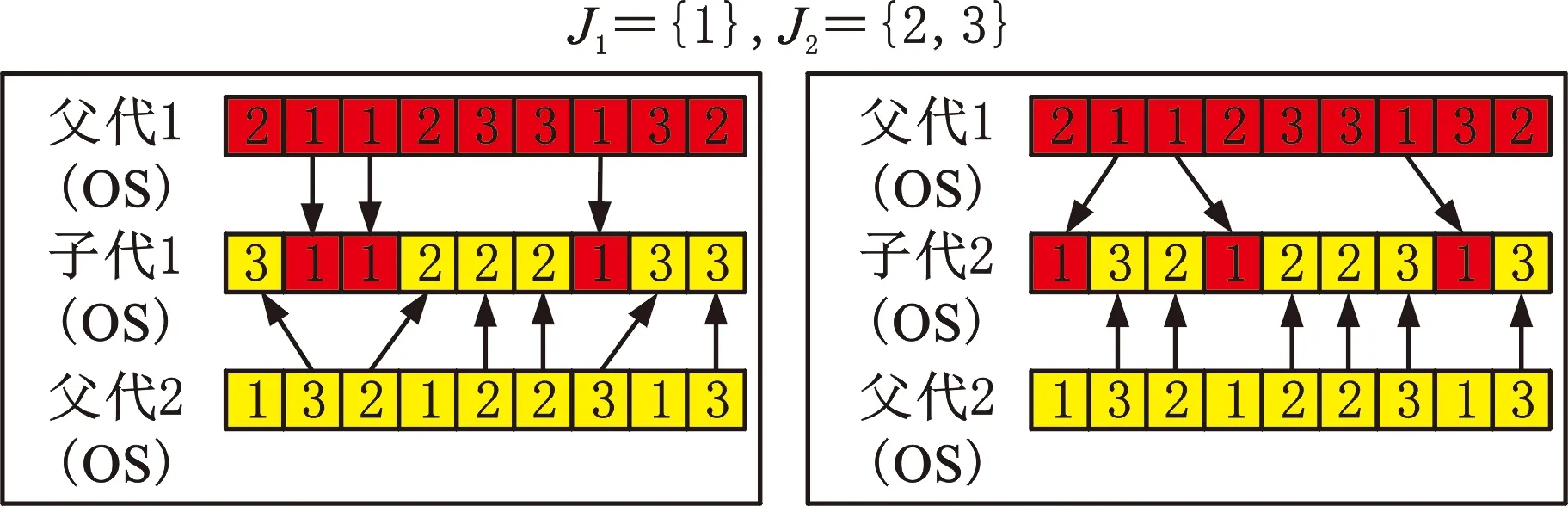
图5 OS POX交叉图

2.2.6筛选个体产生新鸟群

个体交叉生成子代鸟群Q后，将子代加入至原鸟群Y(数量为n)中，将Q和Y合并为R，对R重新进行非支配排序，在非支配解集中随机选择小生境数最小的个体作为新鸟群S的领飞鸟，同时更新S的小生境数；然后按照非支配层等级由低到高将每层个体加入至S中，直至S的数量等于n；若S的飞鸟数量大于n，则需要重新在最后一层非支配层中通过基于参考点的选择算子选择一定数量个体保留在S中，未被选择个体则剔除出S，使S的数量等于n。新鸟群生成如图6所示。

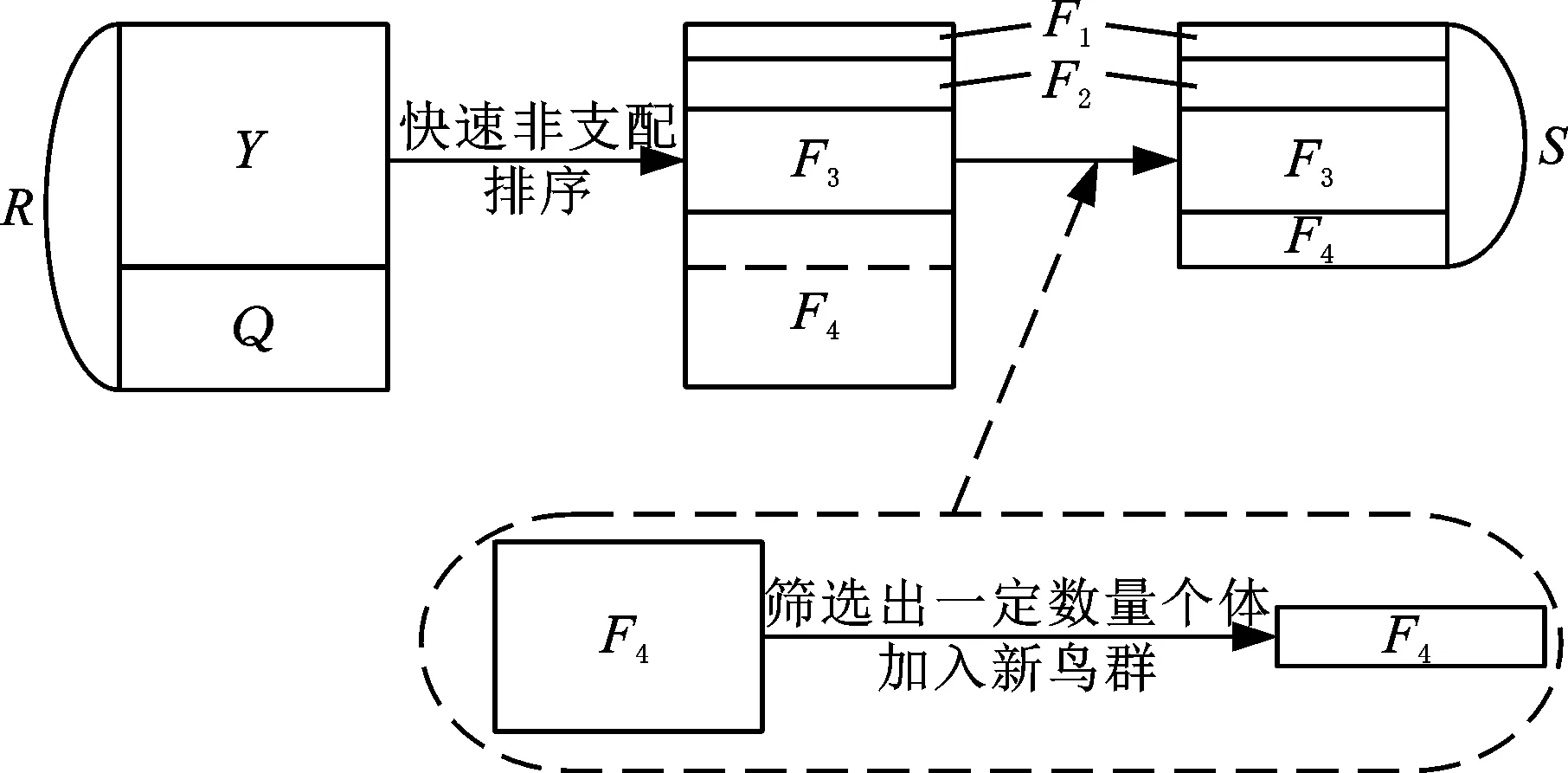
图6 新鸟群生成图

生成新鸟群之后，若未达到最大迭代次数，则返回至鸟群进化阶段进行下一次迭代；若达到最大迭代次数，则将新鸟群的非支配解集作为最终优化结果输出。

2.2.7基于AHM和灰色关联度分析法的组合权重决策

实际生产需要选择一个确定的方案。MOMBO最终的非支配解集可能存在多个解，本节采用组合赋权法进行方案选择。组合赋权是主观赋权和客观赋权的线性加权，其中，主观赋权采用属性层次模型，客观赋权采用灰色关联度分析法。

(1)属性层次模型(attribute hierarchical model，AHM)先将各个指标划分为相互关联的有序结构，再结合专家的主观意见和分析者的判断来确定指标权重。基于AHM 的权重计算方法如下：

①建立判断矩阵A=[aij]，比较同一等级指标之间的重要性，其中，aij=1/aji(i≠j)，aii=1。

②设μ=[μij]为测度矩阵，μij是由aij换算而成的测度指标，令

(11)

k=1，2，…

这里设置β=1。

③计算指标权重。指标主观权重向量Wa=(w1，w2，…，wm)按下式计算：

(12)

其中，w1+w2+…+wm=1且0≤wi≤1。

(2)灰色关联度分析(gray relation analysis，GRA)法的思想是：先根据某个问题的实际情况确定理想的最优序列；然后，通过方案的序列曲线和几何形状与理想最优序列的曲线和几何形状的相似程度来判断方案的序列与理想最优序列之间的关联程度，曲线和几何形状越接近说明关联度越大，方案越接近理想最优，则该方案的权重越大。GRA的主要步骤如下：

①数据规范化处理。假设有n个方案，每个方案有m个目标值，首先对各个指标进行规范化处理，规范化处理计算式为

(13)

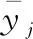
②由下式计算灰色关联系数：

(14)

灰色关联系数反映yij与理想值之间的关联程度。

③权重计算。根据灰色关联系数矩阵计算得到客观权重向量Wb，其中，第j个目标的权重为

(15)

(16)

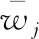
(3)综合权重确定。将AHM得出的权重Wa与灰色关联度分析法的权重Wb结合，求得综合权重：

w*=θWa+(1-θ)Wb

(17)

其中，θ为主观偏重系数，θ∈[0，1]，由决策者依据偏好给出。组合赋权法既能充分利用专家长期积累的生产加工经验，使结果更贴近实际生产，又能在一定程度上从数据本身特性来确定其重要性。

3 性能测试与案例研究

为验证本算法的有效性，首先将MOMBO分别与三个变体、NSGAⅡ及NSGAⅢ的最终解集进行对比，然后通过仿真对MOMBO求得的非支配解集进行分析。本节所有算法均由MATLAB R2014实现，MATLAB在Intel i5-8300H、内存8.00 GB的计算机上运行。

3.1 算法性能测试

本小节通过10个BRdata测试问题[20]来验证MOMBO的性能，将测试问题的加工时间作为本调度问题中各个工序的基本加工时间，算例的其他数据如交货期、机器加工功率、空载功率等数据如表1所示。

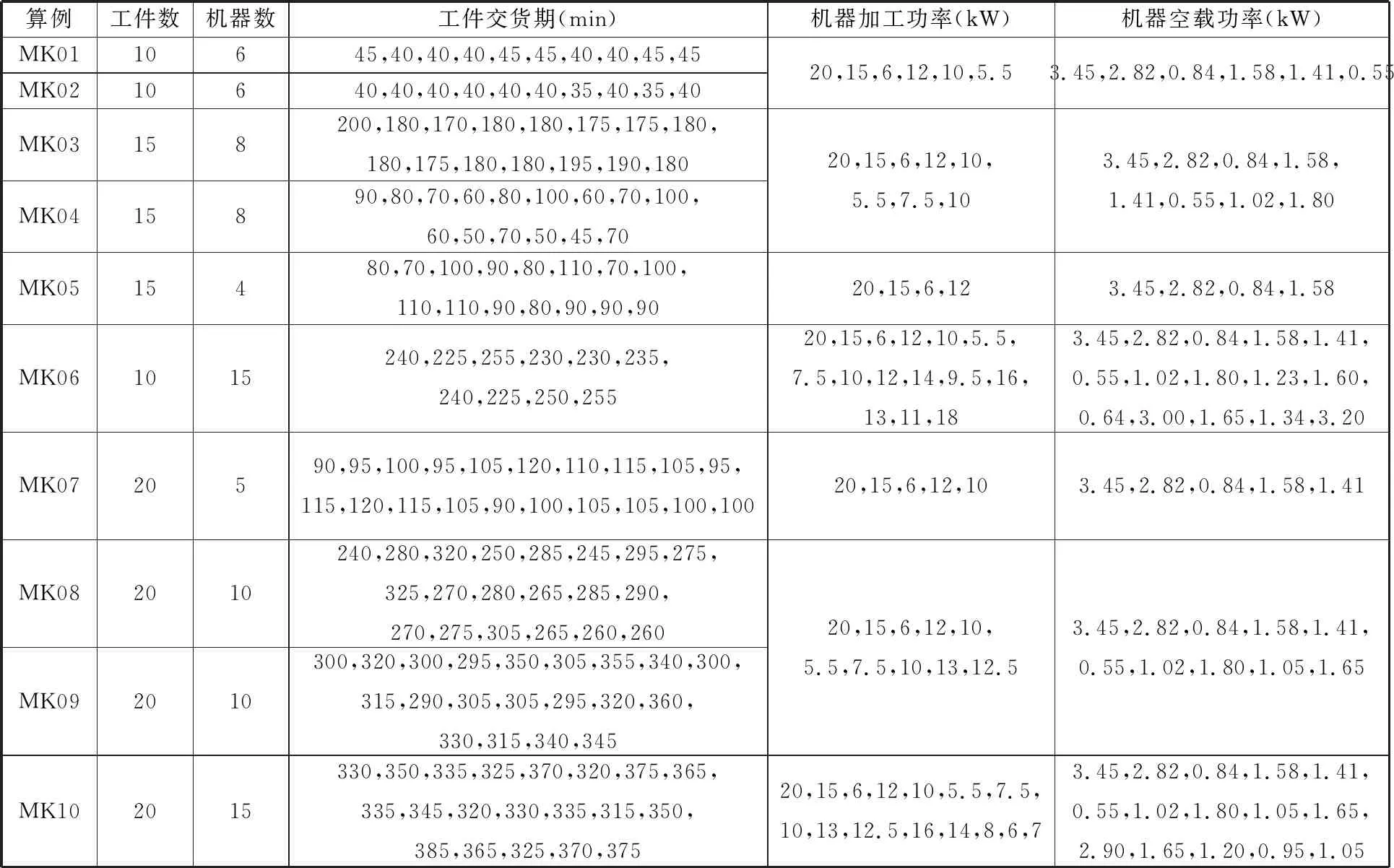
表1 算例数据

多目标优化算法的解集有多种评价指标，本文采用的评价指标是反向世代距离(inverted generational distance，IGD)[21]和超体积(hypervolume，HV)[22]。

IGD能综合评价解集的收敛性和多样性，其计算公式为

(18)

其中，P*为一组理想解集，本文设定为所有算法多次运算后得到的全部解中的非支配解集；|P*|为解集P*中解的个数；x为解集P*中的某个解；解集P是某算法求出的该前沿面的一个近似解集，y是解集P中的某个解；d(x，y)为解x和y在目标空间中的欧氏距离。IGD值越小，算法性能越好。

超体积能综合反映解集的收敛性和多样性，其计算公式为

(19)

其中，解集P是Pareto前沿面的近似解集；fm为解集P中某个非支配解f=(f1，f2，…，fm)T的第m个目标值；r=(r1，r2，…，rm)T为目标空间中的一个参考向量，它被解集P中所有目标向量支配；volume(*)表示近似Pareto前沿面与参考向量所围成的超立方体的超体积。那么关于参考向量r的超体积指的是被解集P所支配且以参考向量r为边界的目标空间的体积。

将超体积定义为被解集P所支配且以参考点r为边界的目标空间的体积，HV(P，r)越大，算法性能越好。对于4个目标的柔性作业车间调度问题，本文采用BADER等[23]提出的蒙特卡罗模拟方法计算HV(P，r)。

3.1.1MOMBO与MOMBO变体的比较

为验证所做改进对MOMBO算法性能的影响，构建以下几种变体类型：

MOMBO1：采用半主动解码。

MBMBO2：种群初始化阶段采用随机初始化方式。

MOMBO3：飞鸟进化过程仅采用N1邻域结构产生邻域解。

MOMBO算法参数设置如表2所示。多次运行MOMBO及其3种变体，求得多个近似解集，然后计算IGD值和HV值，最终取平均值进行对比，结果如表3所示，其中，最优的结果用加粗数字表示。由表3可知，除了算例MK04和MK05，MOMBO算法的IGD值、HV值都优于3种变体算法，由此可知基于MBO算法提出的贪婪插入式解码法、改进的多种初始化规则，以及改进的邻域搜索策略在大部分情况下更适用于高维多目标柔性作业车间调度模型。

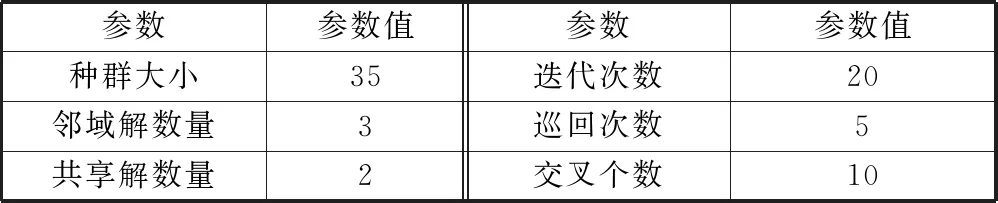
表2 MOMBO参数设置

表3 MOMBO及其变体的IGD、HV

3.1.2MOMBO与NSGAⅡ、NSGAⅢ的比较

NSGAⅡ、NSGAⅢ的参数设置如表4所示。多次运行MOMBO、NSGAⅡ和NSGAⅢ，求得多个近似解集，然后计算IGD值和HV值，最终取平均值进行对比，结果如表5所示，其中，最优的结果用加粗数字表示。由表5可知，MOMBO的IGD值和HV值都显著优于NSGAⅡ和NSGAⅢ，验证了MOMBO求解该问题的有效性。

表4 NSGAⅡ、NSGAⅢ的参数设置

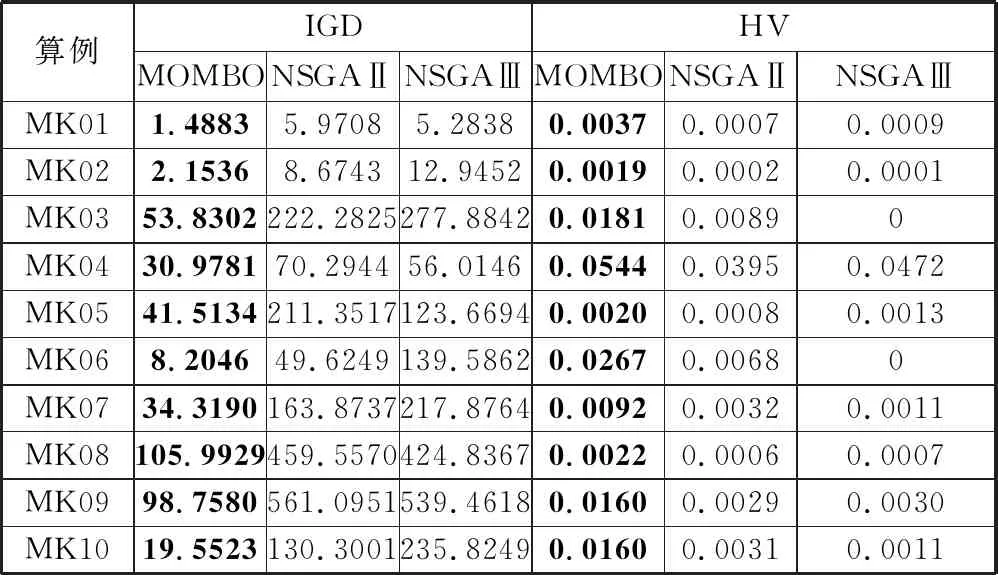
表5 MOMBO、NSGAⅡ和NSGAⅢ的IGD、HV

3.1.3算法收敛性分析

为验证算法运行过程中的收敛性，绘制MOMBO、3种变体、NSGAⅡ和NSGAⅢ的HV值随迭代次数变化的进化轨迹图。由图7可以看出，6种算法的HV值都随着迭代次数的增大而增大，这意味着它们的收敛性能稳定；MOMBO每代的HV值在MK08、MK09算例上远大于其他算法的HV值，说明MOMBO的进化效果最好；MOMBO2、NSGAⅡ、NSGAⅢ的HV值明显小于MOMBO、MOMBO1、MOMBO的HV值，这说明本文提出的多种初始化方式是有效的。接下来考虑非支配解集占比情况，MOMBO求解MK01的初始解集中，非支配等级共有5层，其中，非支配解集占所有解集的比例为28.6%；MOMBO求解MK01的最终解集的非支配等级为4层，其中，非支配解集占所有解集的68.6%。这说明所提出的两种选择算子能给予算法有效的进化压力，能有效促进算法的收敛。

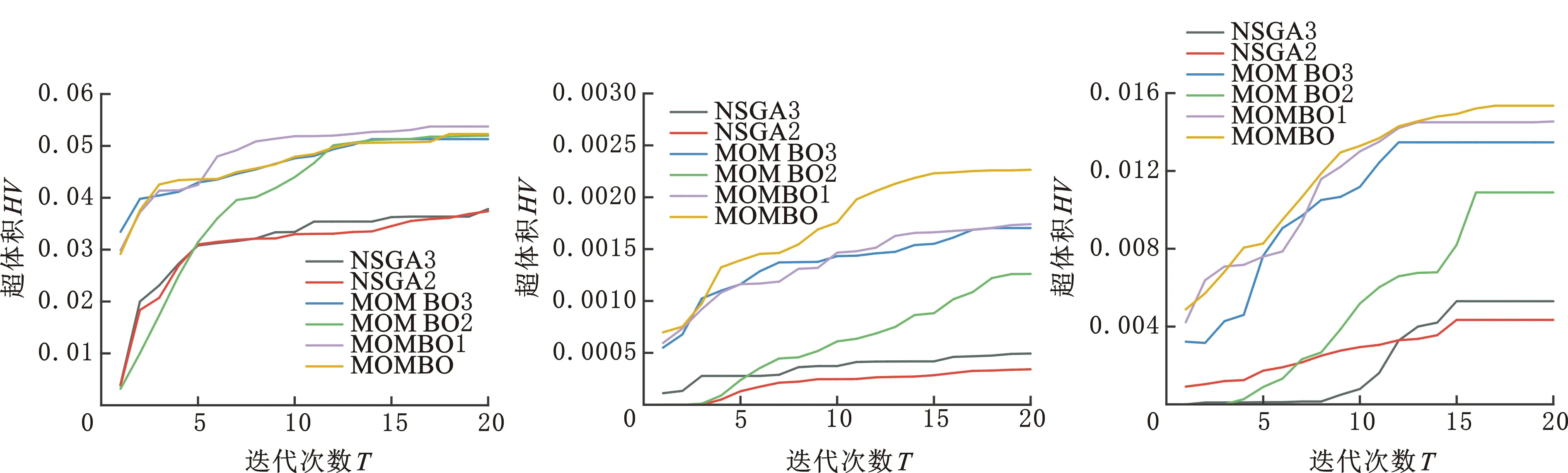
(a)MK04 (b)MK08 (c)MK09

3.2 实例研究

为验证本文算法在实际生产加工中的效果，在某工厂进行加工实验。实验内容是，5台加工机器上加工4个工件，通过Precision Power Analyzer LMG671收集机床加工工件过程中的功率。对得到的数据进行预处理，获得每台机器的加工功率和空载功率曲线图。为方便计算，通过取均值求得各机器的加工功率和空载功率。车间固有功率为2kW，每个工件的交货期和加工时间如表6所示，其中，“-”表示该工序不能在此机器上完成。

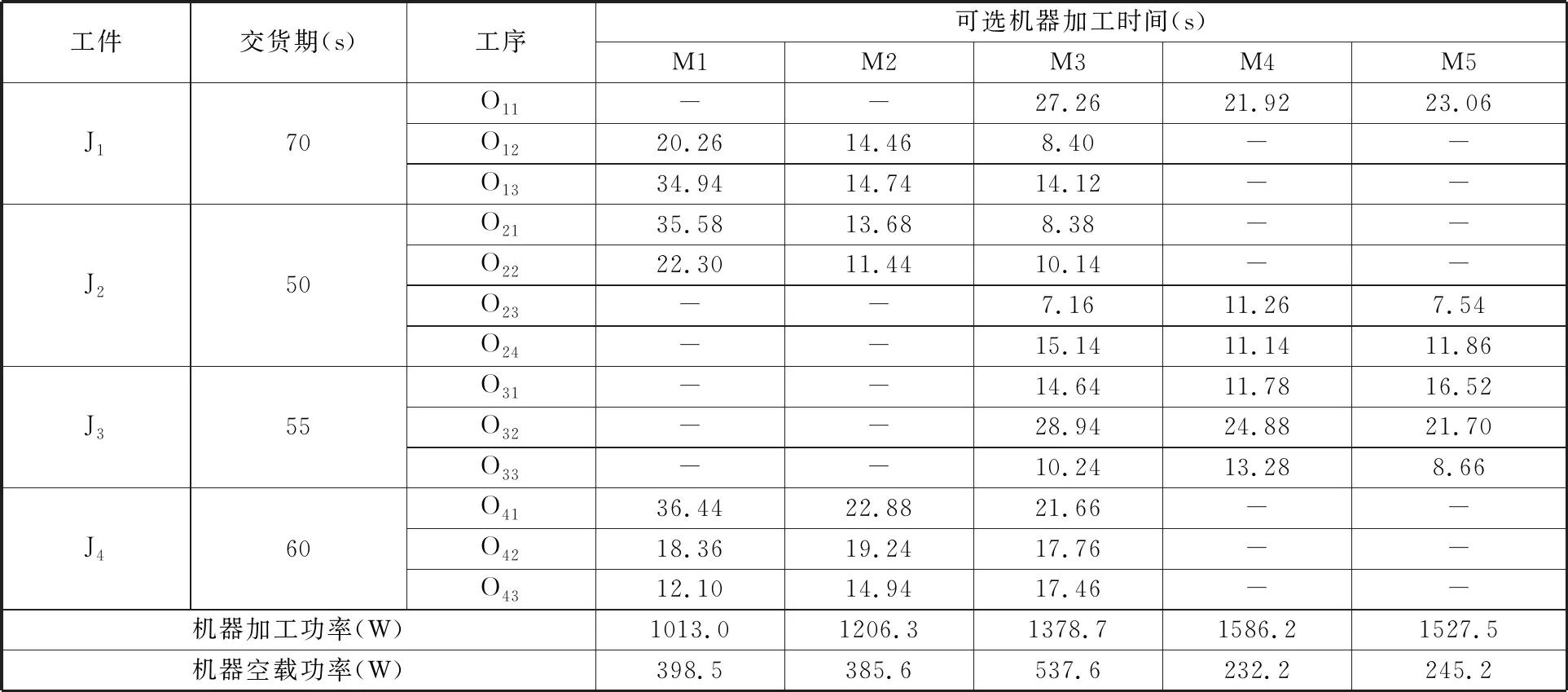
表6 实验数据

3.2.1MOMBO与单目标MBO的比较

通过MOMBO算法求得Pareto前沿解集，如表7所示。通过MBO算法分别求解出以最大完工时间f1、总拖期f2、机器最大负荷f3、总能耗f4为目标的单目标最优解，如表8所示。观察表8可以发现，虽然单目标最优解在某个目标值上最优，但其他3个目标值较差，单目标最优解与通过MOMBO算法求出的最优解集中的某个解的目标值之差即Δf1～Δf4如表9所示。由表9可见，在MOMBO求出的最优解集中，总能找出优于单目标最优解的解，因此通过MOMBO求出的最优解集相对于单目标最优解具有更好的质量。

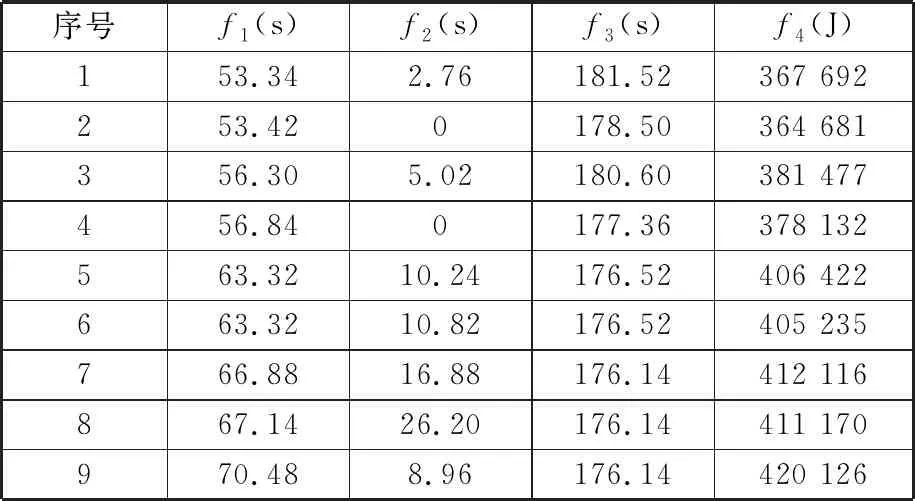
表7 实例Pareto前沿解集

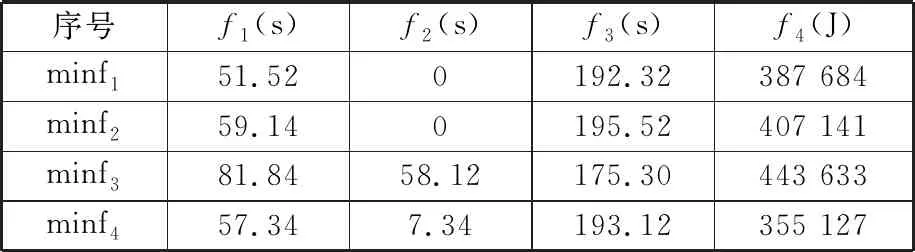
表8 实例单目标最优解

表9 单目标最优解与多目标最优解的目标值之差

3.2.2MOMBO与NSGAⅡ、NSGAⅢ的比较

NSGAⅡ、NSGAⅢ求得的最优解集分别如表10、表11所示。对比表7可以看出，MOMBO求出的最优解大部分都优于NSGAⅡ、NSGAⅢ求得的解。为进一步对比MOMBO与NSGAⅡ、NSGAⅢ的收敛性和多样性，通过式(18)、式(19)求得3种算法的IGD值和HV值，如表12所示。在求解过程中，本文设定P*为三种算法多次运算后得到的非支配解集。如表12所示，对于本实例，MOMBO取得了优于另外2个算法的结果。

表10 NSGAⅡ的实例Pareto前沿解集

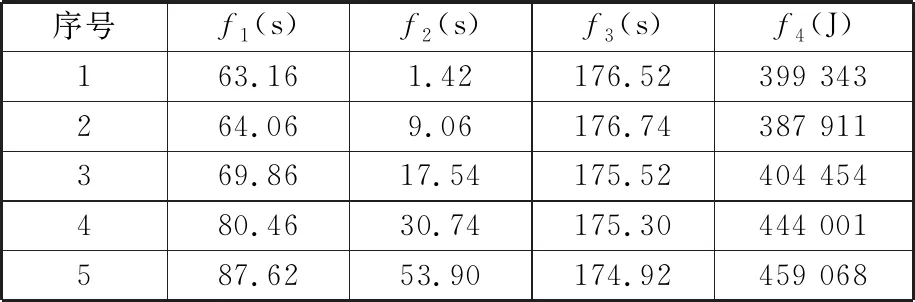
表11 NSGAⅢ的实例Pareto前沿解集

表12 MOMBO、NSGAⅡ和NSGAⅢ求解实例的结果

图8、图9所示为3种算法求解实例的HV值和IGD值随迭代次数的进化曲线。3种算法的HV值都随着迭代次数的增大而增大，IGD值均随着迭代次数的增大而减小，这说明它们的收敛性能稳定。本文提出的MOMBO的HV值大于另外两种算法的HV值，IGD值小于另外两种算法的IGD值，因此MOMBO的进化效果最好。

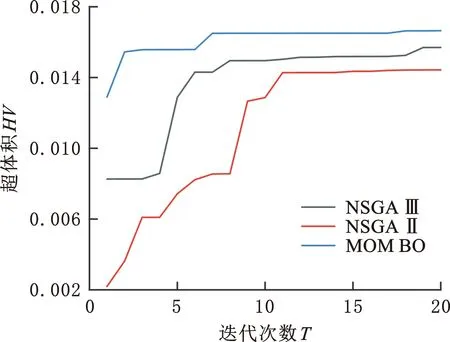
图8 3种算法求解实例所得HV值随迭代次数的进化轨迹

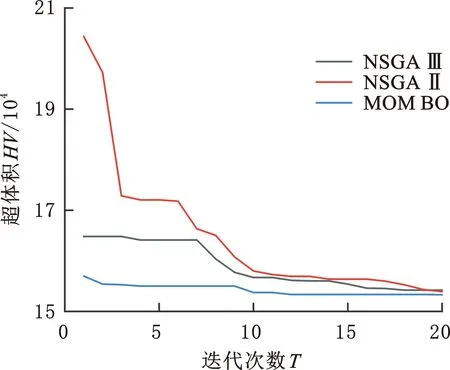
图9 3种算法求解实例所得IGD值随迭代次数的进化轨迹

3.2.3基于组合权重法的最优方案决策

首先根据专家对不同目标的打分情况建立AHM需要的判断矩阵，然后通过计算得到各个目标的主观权重向量Wa=(0.264，0.361，0.264，0.111)；接着根据表7中的Pareto前沿解集计算出灰色关联度分析法的各个数据：

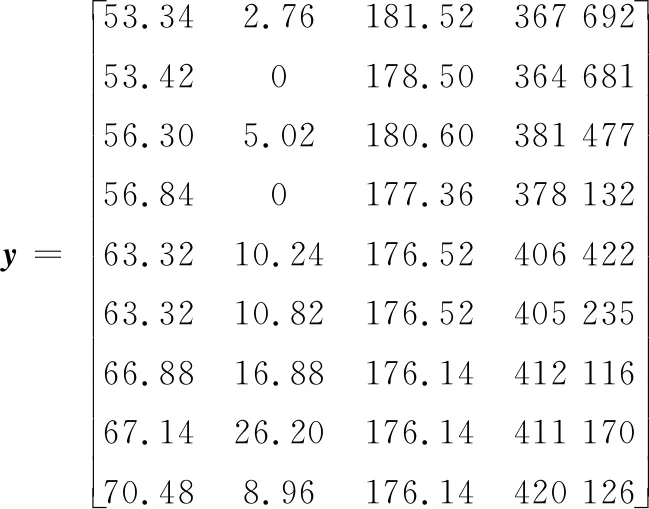
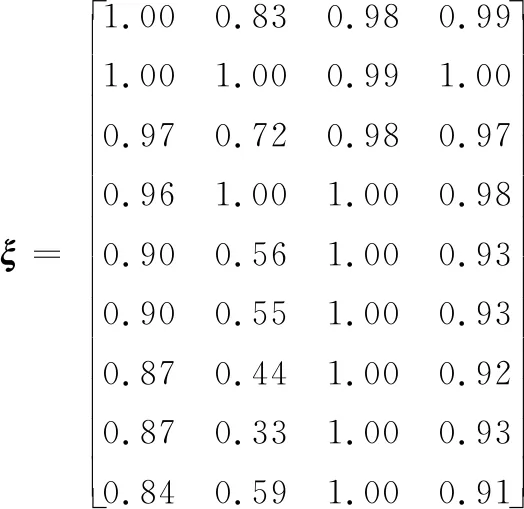
Wb=(0.261，0.189，0.281，0.269)

进一步取θ=0.5，求得综合权重w*=(0.263，0.275，0.272，0.190)。由于本文是逆指标，故需要对y采用减法一致法处理得到y′，即利用每一列的最大值Mj依次减去该列的原始数据，然后将y′×w*，得到最终得分矩阵：

由R可知第二组方案的得分最高，其加工时间为53.42 s，拖期为0 s，机器负载为178.50 s，总能耗为364 681 J。图10为按第二个调度方案加工的甘特图。

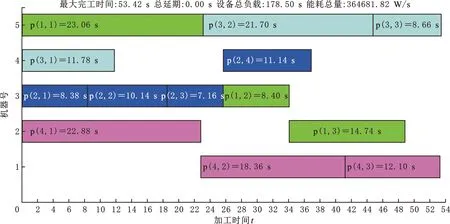
图10 解2的甘特图

4 结论

本文提出以最小化最大完工时间、总拖期、机器总负荷、总能耗为目标的高维多目标柔性作业车间调度模型，并运用一种MOMBO进行求解。算法性能测试表明MOMBO相对于其3种变体以及NSGAⅡ、NSGAⅢ来说，其最优解集在IGD和HV两种性能指标上表现更优。实例研究证明本文提出的MOMBO算法相对于单目标MBO算法、NSGAⅡ和NSGAⅢ有着更好的解集质量，在实际生产加工中能够给予决策者更好的选择。