基于改进非支配排序遗传算法的多目标柔性作业车间低碳调度

姜一啸 吉卫喜，2 何 鑫 苏 璇

1.江南大学机械工程学院，无锡，214122 2.江苏省食品制造装备重点实验室，无锡，214122

0 引言

随着生产力的发展、科技水平的不断提高，制造业发展迅速，但随之而来的却是能源消耗的增加以及生态环境的破坏[1]。机械制造业作为国民经济发展的基础性行业，是实现绿色发展和科技创新的关键领域[2]。车间调度作为制造系统中的关键环节，调度方案会对加工效率、成本、碳排放等产生影响，因此，通过生产调度优化实现绿色生产已成为企业节能减排，提高经济、社会效益的重要途径。

作业车间调度问题(job shop scheduling problem，JSP)已被证明为NP-hard问题[1]，柔性作业车间调度问题(flexible job shop scheduling problem，FJSP)作为JSP问题的延伸，更符合企业实际生产与社会发展需求，逐渐成为本领域研究的重点[2]。近年来，随着社会各界对绿色制造、低碳生产的重视，碳达峰与碳中和“双碳”战略目标的提出[3]，越来越多的车间调度研究开始将绿色低碳作为优化目标，也取得了较多研究成果。刘彩洁等[4]结合分时电价政策，通过合理安排调度任务避开工业用电高峰，构建了以最小化能耗碳排放、能耗成本与最长完工时间为目标的调度模型，并设计了一种基于动态控制参数的快速非支配排序遗传算法对该模型进行求解。WU等[5]考虑设备开机、关机与设备调速两种节能措施，设计了一种能耗模型来计算设备不同状态下产生的能耗，并提出了一种绿色调度启发式算法来同时优化完工时间与能耗。ASSIA等[6]将以最小化最长完工时间与能耗为目标的调度问题抽象成一种二元整数线性规划模型，并通过分支界定算法验证了该模型的可行性。杨冬婧等[7]针对能耗约束条件下的总延迟最小化问题，将该能耗约束问题转化为以最小化总能耗和总延迟为目标的双目标低碳调度问题，并提出了一种新型蛙跳算法进行求解。李明等[8]针对具有准备时间和关键目标的柔性作业车间低碳调度问题，设计一种新型帝国竞争算法，在优化关键目标的同时兼顾非关键目标的改进。综上，现有研究大多侧重于问题本身的模型建立、求解方法的性能优化或是通过不同的节能减排方法来实现低碳调度，而车间作为一个复杂的生产环境，具有多种产生碳排放的途径，因而考虑不同来源的碳排放对于低碳调度研究有着积极的意义。

由于需要在传统经济型指标的基础上同时考虑绿色指标，低碳调度问题必然是更为复杂的多目标决策问题。针对这类多目标优化问题，传统的基于经验的生产规则难以得到优质解，而作为元启发式方法中运用最为广泛的进化算法成为了解决该类问题的关键。其中，DEB等[9]提出的带精英策略的非支配排序遗传算法(non-dominated sorting genetic algorithm，NSGA-Ⅱ)由于采用了快速非支配排序方法、引入了精英保留策略与拥挤度比较算子，因而具有运行速度快、解集收敛性好等优点，被广泛应用于车间调度问题的求解中。HAN等[10]提出了一种改进的NSGA-Ⅱ对多目标FJSP进行求解，通过采用可变邻域结构的局部搜索方法来提高NSGA-Ⅱ的搜索能力。LI等[11]在求解具有多排车间布局的FJSP时，在NSGA-Ⅱ中集成了两种启发式选择策略，通过对迭代结果进行优化，进一步提高算法的搜索性能。JIANG[12]采取一种改进的精英策略来动态调整NSGA-Ⅱ的精英解集，并优化了非支配排序算法，然后通过多目标JSP算例验证了改进算法具有更强的全局搜索能力与求解效率。CHEN等[13]设计了一种具有相对变异性的改进非支配遗传算法，该算法通过计算两条染色体之间的血缘关系来确定染色体突变率，从而避免群体早熟，并通过实例对算法性能进行了验证。宋存立[14]对NSGA-Ⅱ的变异算子与选择方法进行了改进，提高种群多样性的同时兼顾了算法的局部搜索能力，并通过实验案例验证改进算法的有效性。LIANG等[15]针对NSGA-Ⅱ中的交叉与变异存在盲目定向的问题，设计了一种基于个体拥挤度与种群平均拥挤度的交叉、变异算子，提高了算法的收敛速度，然后提出了一种分层选择策略以提高后代种群的多样性，并用该算法对车辆生产调度问题进行求解。可以发现，收敛性优化与多样性改善是NSGA-Ⅱ在车间调度领域的研究热点，上述研究通过改进遗传算子与精英保留策略，或是采用局部搜索与全局改善机制等方法，对NSGA-Ⅱ在收敛性、多样性等方面的不足进行了优化，取得较优结果。但上述改进算法少有从自适应角度考虑，并且已有的适应性策略往往忽略了不同进化阶段对算法性能的需求，同时有关种群初始化的研究相对较少，而初始种群的质量对算法的收敛性有着显著的影响[16]。

本文将设备能耗、刀具磨损及切削液消耗作为车间生产过程中碳排放的来源，考虑包含人工、能耗两部分组成的加工成本，以最小化碳排放量、最长完工时间和加工成本为目标，建立柔性作业车间低碳调度模型，针对该模型，提出了一种改进NSGA-Ⅱ进行求解。通过经典算例和实际案例来验证了所提算法的可行性。

1 问题描述与模型的建立

1.1 问题描述

本文研究的多目标柔性作业车间低碳调度问题可以被描述如下：车间有n个待加工工件，记为工件集J={J1，J2，…，Jn}，有m台加工设备，记为设备集M={M1，M2，…，Mm}，每个工件Ji包含多道工序，每道工序Oij可以在M中的一台或多台设备上进行加工，同一道工序在不同设备上的加工时间、加工成本及产生的碳排放量不同，不同的设备可以在同一时刻加工不同的工件。本文研究问题的目标是确定每道工序的加工设备及各个设备上工件的加工顺序，从而实现碳排放量、最长完工时间和加工成本的最优组合。

在生产调度中，设备能耗、刀具磨损与切削液消耗产生的碳排放与加工过程相关[17]，同时，由于设备的不同，员工岗位、技能水平的差异，同一个工件的同一道工序在不同的设备上加工的能耗、人工费用也各不相同。因此，本文以设备能耗、刀具磨损与切削液消耗作为碳排放的来源，以设备、人工费用作为加工成本。描述问题与建立模型过程中所需的符号与含义见表1。

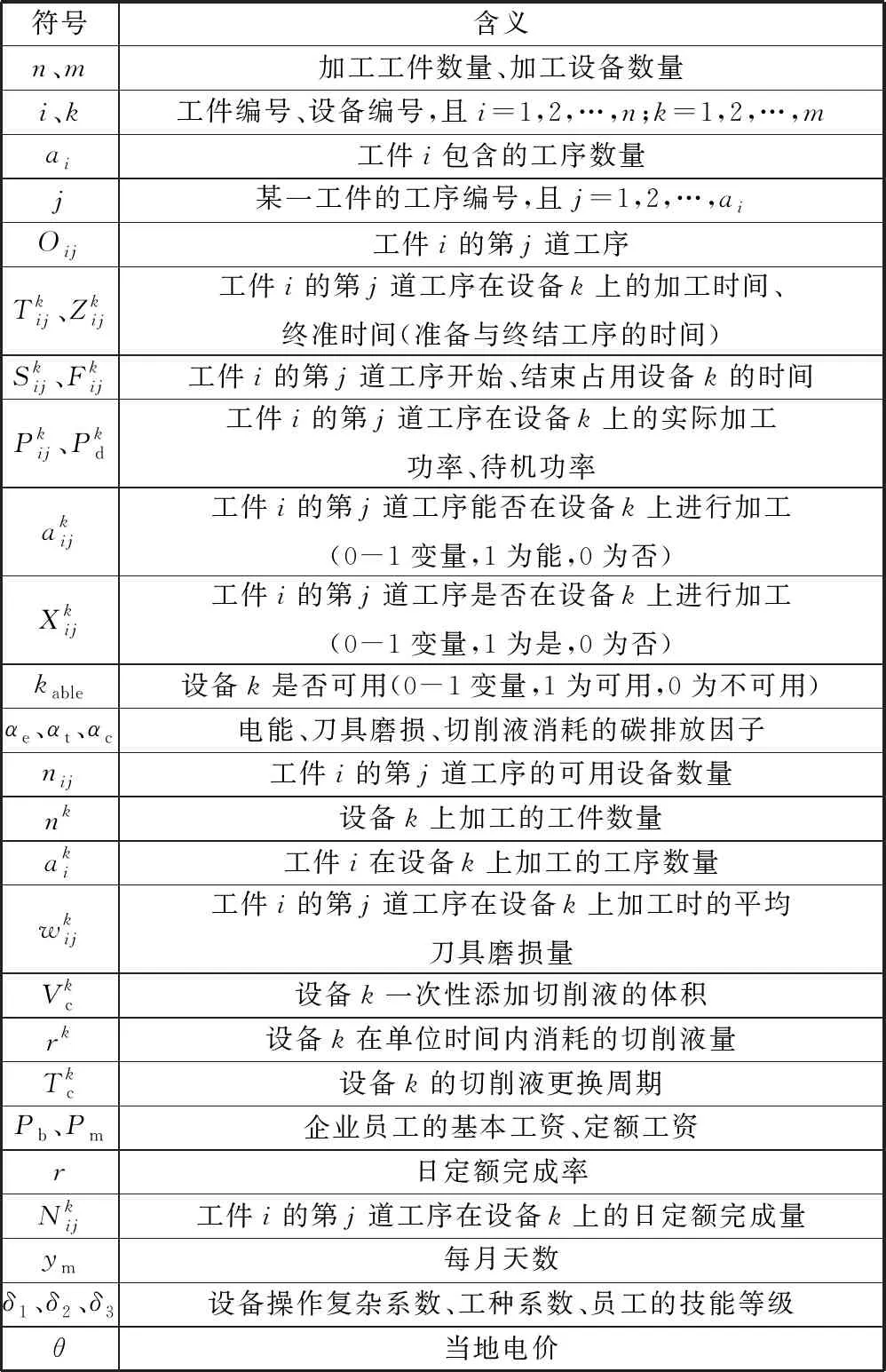
表1 模型符号及含义

1.2 模型的建立

本文针对柔性作业车间的特点，以最小化碳排放量FC、最长完工时间FT和加工成本FP为目标函数建立数学模型：

(1)

(2)

(3)

(4)

(5)

(6)

设备k上因切削液消耗而产生的碳排放可表示为

(7)

(8)

(9)

模型的约束条件如下：

(10)

(11)

(12)

(13)

t=0，∀kable=1

(14)

(15)

式(10)表示工序的加工过程不能中断；式(11)表示工件的工序加工存在先后顺序，前一道工序完成才能进行后一道工序的加工；式(12)、式(13)表示同一时刻，工件的某道工序只能由其可用设备中的一台进行加工；式(14)表示所有设备在0时刻均可用。式(15)表示工序分配设备时，所有可用设备都具有相同的优先级。

2 低碳策略下的改进NSGA-Ⅱ

传统NSGA-Ⅱ在求解多目标问题时，存在初始种群质量、交叉变异率、保留策略等方面的局限性，使得算法搜索效果较差且易陷入局部最优。因此，本文提出了一种改进NSGA-Ⅱ：①设计了一种种群初始化方法，通过Tent混沌映射生成较为均匀、多样的初始种群，并在传统贪婪解码的基础上结合AHP进一步提高初始种群质量；②设计了考虑种群进化阶段及个体质量的遗传策略；③设计了一种基于外部档案集的改进精英保留策略，避免了进化后期种群多样性降低以及可能收敛于非第1支配面的问题，同时保护了优质个体不在遗传过程中被破坏。改进NSGA-Ⅱ流程如图1所示。

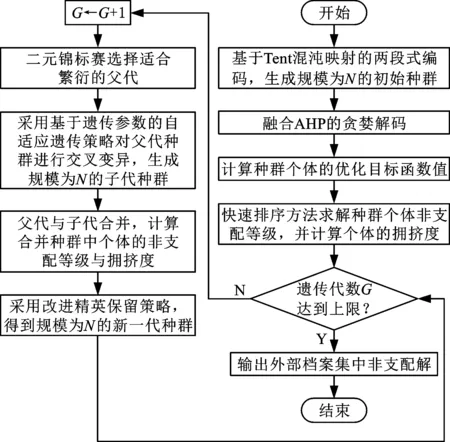
图1 改进NSGA-Ⅱ流程图

2.1 种群初始化

初始种群的质量对算法的结果及全局收敛性有很大的影响[19]。车间调度问题不仅需要给出工件的加工顺序，还要为每道工序分配相应的机器，为此，本文采用Tent混沌映射生成基于工序码和设备码的初始种群，相比经典的Logistic混沌映射，Tent混沌映射得到的种群具有更好的随机性、均匀性与多样性，具体表达式如下：

(16)

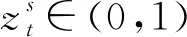
(17)

其中，rand(0，1)为[0，1]之间的随机数；NT为已有的混沌变量数量。

具体的编码过程如下：

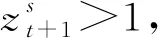
(2)将第一组混沌变量与原始工序一一对应，按照混沌变量的大小进行降序排列，并将对应的工序进行相应的重排，最终得到的工序序列即为工序码，见表2。

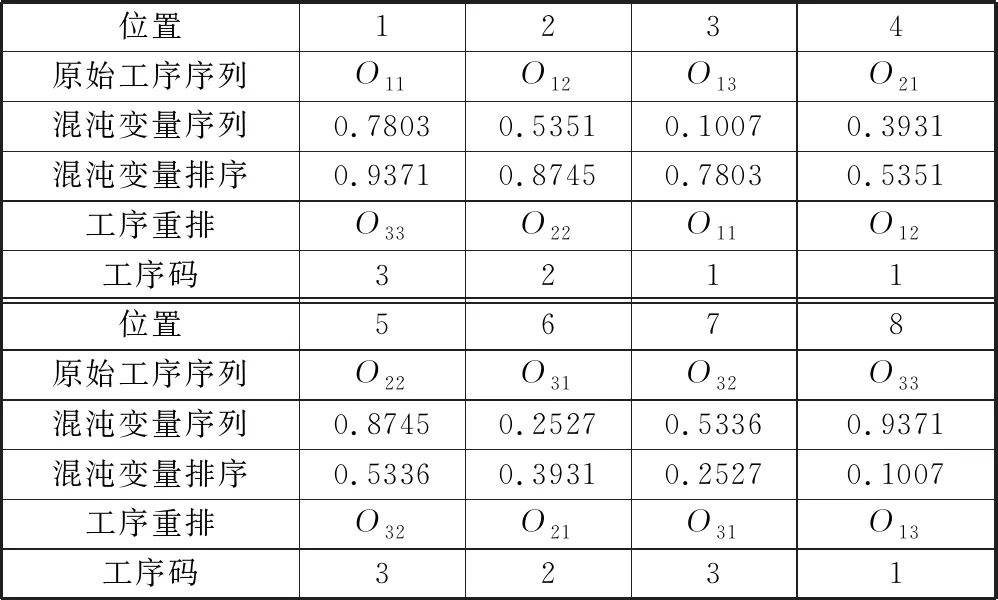
表2 工序码编码示意

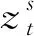
(18)

(4)重复上述操作，直至达到种群数量。

解码是一种将编码得到的染色体还原成实际加工信息的过程。由于初始种群的质量较差，设备利用率不高、存在的加工间隙较多，在多目标调度问题中，传统的插入式贪婪解码只能保证提高设备利用率，缩短完工时间，却难以保证其他目标的优化，为此本文提出了一种融合层次分析法(analytic hierarchy process，AHP)的贪婪解码方法，通过引入AHP分析判断贪婪策略对种群的影响，避免传统贪婪解码会影响后续工序安排、难以保证全局优化的问题，从而提高初始种群的质量。具体步骤如下：

(1)将通过Tent混沌映射得到的染色体按顺序进行解码操作，在解码过程中通过下式判断当前基因位置对应的工序Oij能否插入该工序可加工设备中现有的加工间隙中：

(19)

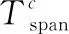
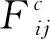
(2)假设Mini与满足步骤(1)中条件的待选设备Mc的总数量为p，优化目标数量为q，对各优化目标函数值进行min-max归一化操作如下：

(20)

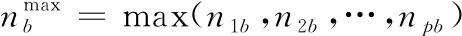
其中，a为设备序号，a=1，2，…，p；b为优化目标序号，b=1，2，…，q；nab为优化目标b在设备a上的取值。进而得到在不同设备上加工的优化目标决策矩阵m=(mab)p×q。

(3)采用AHP计算权重向量，具体步骤如下：

①构造判断矩阵A，表达式如下：

(21)

其中，fq为各优化目标，矩阵中的元素代表两个优化目标之间的相对重要度，用1～9表示，1、3、5、7、9分别表示“同等重要”“稍微重要”“较强重要”“强烈重要”与“极端重要”，2、4、6、8分别表示两相邻判断的中间值。

②计算判断矩阵A的最大特征根λ与其对应的经归一化后的特征向量ω。

③对判断矩阵A进行一致性检验，一致性指标定义如下：

(22)

其中，σ为矩阵阶数。定义一致性比率RC=IC/IR，IR为随机一致性指标。当RC<0.1时，认为该判断矩阵有满意的一致性，对应的特征向量ω就作为权重向量，若不满足，则需要对判断矩阵进行进行调整。随机一致性指标IR的取值见表3。

表3 随机一致性指标IR标准值

(4)取向量mωT中最小值对应的设备为工序Oij插入的设备，若对应的设备为初始分配设备Mini，且该设备上存在满足插入条件的间隙，则将工序Oij向前插入，否则仍保留原方案。

(5)当发生插入操作时，染色体组成需要进行动态调整以保证遗传信息的准确。将工序码与设备码中当前基因的位置进行前移，同时将设备码中对应基因位置的设备号替换成插入的加工间隙所在的设备号。工序Oij对应的基因在染色体中的新位置pos(Oij)如下：

(23)

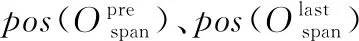
2.2 非支配排序与拥挤度计算

本文采用一种快速排序方法[21]来进行非支配排序，该方法定义了一种新的支配关系“≻d”(超级支配关系)，如果A支配B，或A与B不相关(A、B互不支配)，则A≻dB。该方法相较于传统的NSGA-Ⅱ，平均时间复杂度从O(mN2)降到O(qNlogN)(q为优化目标数量，N为种群规模)，具体步骤如下：

(1)从序列集S(种群所有个体构成的集合)中第1个个体x1开始，将x1与其之后个体进行“≻d”比较。一轮比较之后将S分成两部分，一部分为被x1支配的个体，这部分个体必不为当前种群的非支配个体；另一部分为“超级支配”x1的个体，这部分个体组成新的序列集S′。若x1不被S′中的个体所支配，则x1为当前种群的非支配个体，将其并入非支配解集中。

(2)在新的序列集S′中重复步骤(1)中的操作，直至S′中只有1个个体。

(3)将S中属于当前非支配解集的个体删除，重复上述操作，直至所有个体的非支配等级都分配完毕。

得到种群个体的非支配等级后，进一步计算各非支配等级中个体的拥挤度ld，具体计算公式如下：

(24)

2.3 选择操作

采用二元锦标赛选择法选择进行交叉变异的父代种群，具体步骤如下：

(1)从初始种群中任选两个个体进行比较，优先选择非支配等级高的个体；若两者非支配等级相同，则优先选择拥挤度较高的个体；若两者拥挤度相同，则从中任选一个。

(2)重复步骤(1)，直至选出N个个体作为父代种群。

2.4 交叉、变异操作

交叉率、变异率对算法全局收敛性有很大的影响[22]，已有的自适应遗传策略大多只模拟了交叉个体对环境的反应，而没有考虑不同进化阶段对交叉率、变异率的要求。在算法初期，种群质量较差，应赋予相对较高的交叉率和变异率以提高种群质量；在算法后期，种群质量相对优秀并且较为稳定，应逐渐减小交叉率和变异率，保护优秀的基因不被破坏，并避免算法搜索停滞。由于多目标优化问题中各目标之间存在耦合，同时为避免算法搜索过程变成随机搜索，变异率不宜超过0.1[22]，交叉率的范围应为[0.9，1][23]。因此，本文在已有自适应策略[24]的基础上，设计了一种基于遗传参数的自适应遗传策略，根据种群进化阶段以及种群个体的支配情况动态调整交叉率Pj和变异率Pb，具体表达式如下：

(25)

(26)

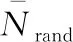
当交叉、变异对象的非支配等级较高，即染色体质量较差时，以最大交叉率和变异率促进个体进化；当交叉、变异对象的非支配等级较低，即染色体质量较好时，根据种群进化阶段适当降低交叉、变异率，同时，若当前种群非支配层数R较大，即种群整体收敛性较差时，可适当提高交叉率、变异率来加快种群收敛。特殊地，若当前种群所有个体都互不支配，即所有个体非支配等级均为1，以最大交叉率和变异率来提高种群多样性。

交叉操作通过交换种群个体之间部分基因片段生成新的个体，变异操作通过改变种群个体自身基因片段来丰富种群多样性。由于工序码与设备码的编码规则不一致，故两者的交叉、变异操作也有所不同，分别进行说明如下。

采用模拟二进制交叉(simulated binary crossover，SBX)来交替进行工序码与设备码的交叉。

工序码的交叉过程(图2a)如下：从父代种群中随机选择两个个体，将其工序码作为父代P1和P2，随机生成一个工件列表J，J中记录将要进行交叉的工件号。将P1中属于J中工件的信息与P2中不属于J中工件的信息保留下来，生成子代C1，将P1中不属于J中工件的信息与P2中属于J中工件的信息保留下来，生成子代C2。

设备码的交叉过程(图2b)如下：从父代种群中随机选择两个个体，将其工序码和设备码作为父代P1和P2，随机生成一个位置列表J，确定P1工序码中属于J中位置的工序，将其对应的设备与P2中对应工序的设备相交换，生成对应的子代设备码C1和C2。

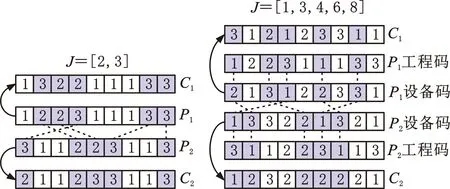
(a)工序码交叉 (b)设备码交叉

采取互换基因的方式进行工序码变异：随机选择父代工序码P中的两个基因进行位置交换，生产子代C，如图3a所示。

采取双基因变异的方式进行设备码变异：随机选择父代工序码P中的两个基因，从这两个基因对应的可用设备集中任选一个与当前不同的设备进行替换生产子代C，如图3b所示。

(a)工序码变异 (b)设备码变异

2.5 改进精英保留策略

传统的精英保留策略通过非支配关系与拥挤度保留父代与子代合并种群中的前N个个体作为新一代种群，但随着种群的进化，大量的个体聚集于第1非支配等级，种群多样性降低，并且前期得到的优质个体可能在进化中被破坏，难以在整个遗传过程中被保留。因此，本文提出了一种基于外部档案集的改进精英保留策略，通过设计一种概率分布函数代替传统按非支配等级与拥挤度大小确定的保留策略，该概率分布函数根据种群进化状况为不同非支配等级的个体添加相应的保留概率。算法初期种群质量较差，优质个体应有较大的概率被保留，加快种群的进化，算法后期第1非支配等级个体大量增加，提高了其他非支配等级的个体被保留的概率，保证了种群多样性，避免陷入局部最优。同时，建立一个大小为N的外部档案集，用于存放保留下来的非支配个体，并通过非支配关系对其进行更新。具体分布函数如下：

Nd=rdFd

(27)

(28)

式中，d为非支配等级(d≥1)；Nd为第d级非支配等级上保留的个体的集合；Fd为第d级非支配等级所有个体的集合；rd为第d级非支配等级上个体被保留的概率；nd为第d级非支配等级上的个体数。

基于外部档案集的改进精英保留策略的步骤如下：

(1)将父代与子代合并成大小为2N的新种群，重新进行非支配等级与拥挤度计算。

(2)从非支配等级为1的个体开始，按对应非支配等级的保留概率判断是否保留该个体，当保留下来的个体数量达到N时停止操作。

(3)若遍历完所有非支配等级后保留的个体数量小于N，则对剩余个体继续进行上述操作，直至找出N个个体作为新一代种群。

(4)将新一代种群中的个体并入外部档案集，并重新进行非支配排序与拥挤度计算，保留其中最优秀的前N个个体。

3 仿真实验

本文分别以经典BRdata[25]调度算例和一个实际加工案例为对象，将改进NSGA-Ⅱ与传统NSGA-Ⅱ和引入参考点选择的非支配遗传算法(reference-point-based non-dominated sorting genetic algorithm，NSGA-Ⅲ)[26]进行对比。运行环境为Windows 10操作系统，采用MATLAB R2016a进行算法实现。

3.1 算法性能评价指标

本文选择Cov指标[27]、Spacing指标[28]与HV指标[29]从不同方面对算法性能进行评价，由于各优化目标的量纲不同，故计算指标时需先对各目标进行归一化处理。

Cov指标可以反映两个非支配解集间的互相支配程度，其具体定义如下：

(29)

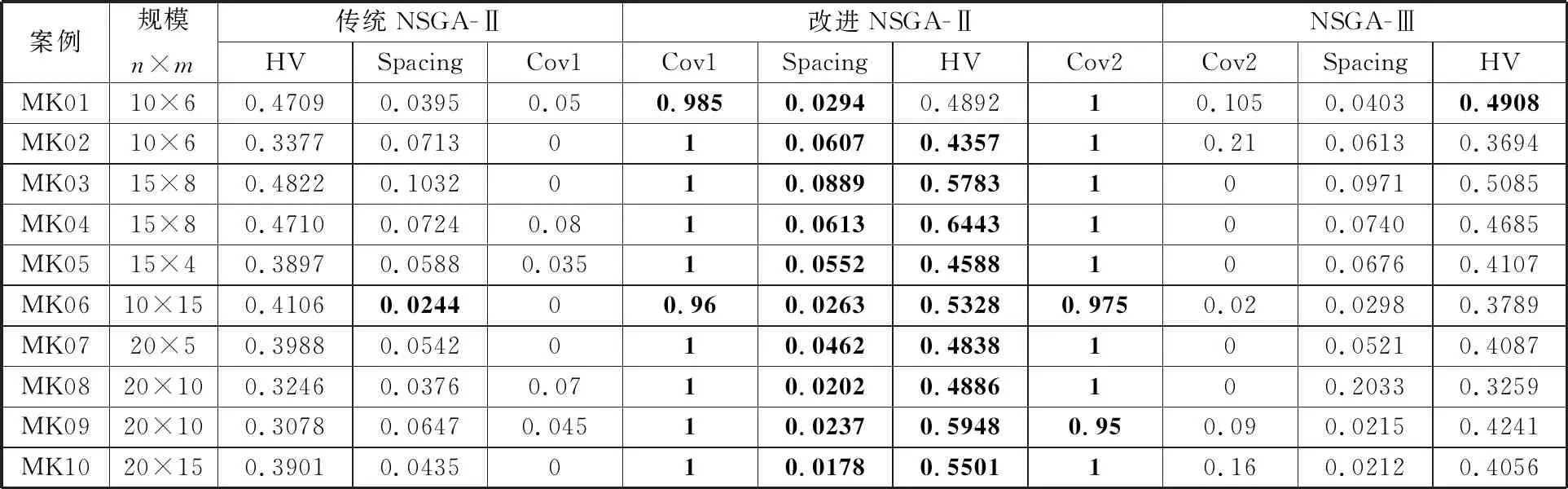
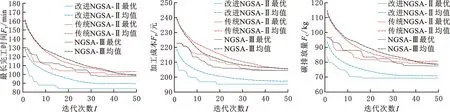
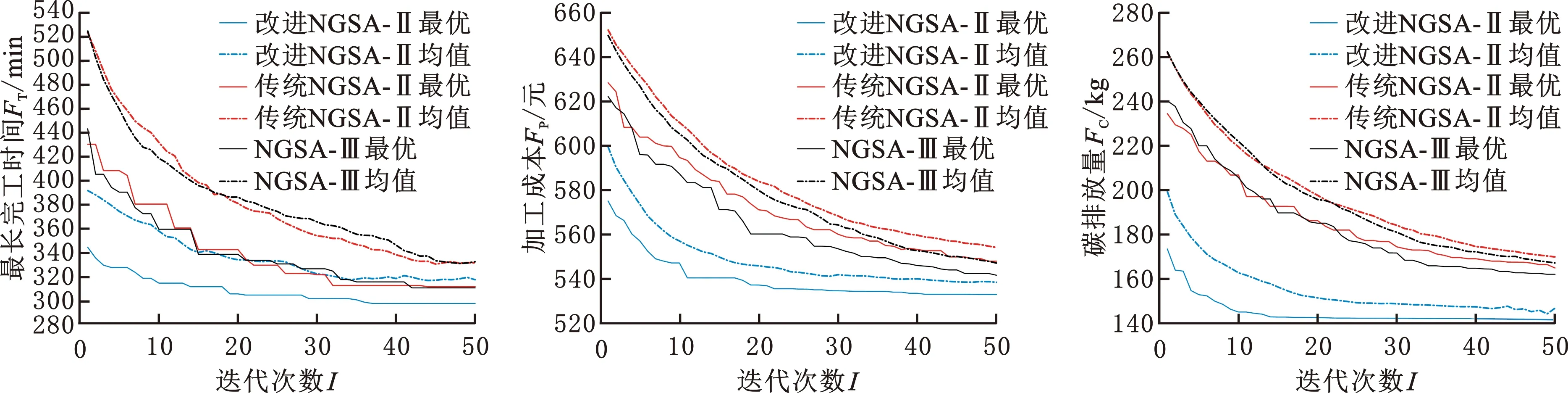
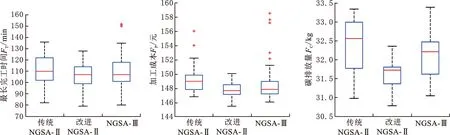
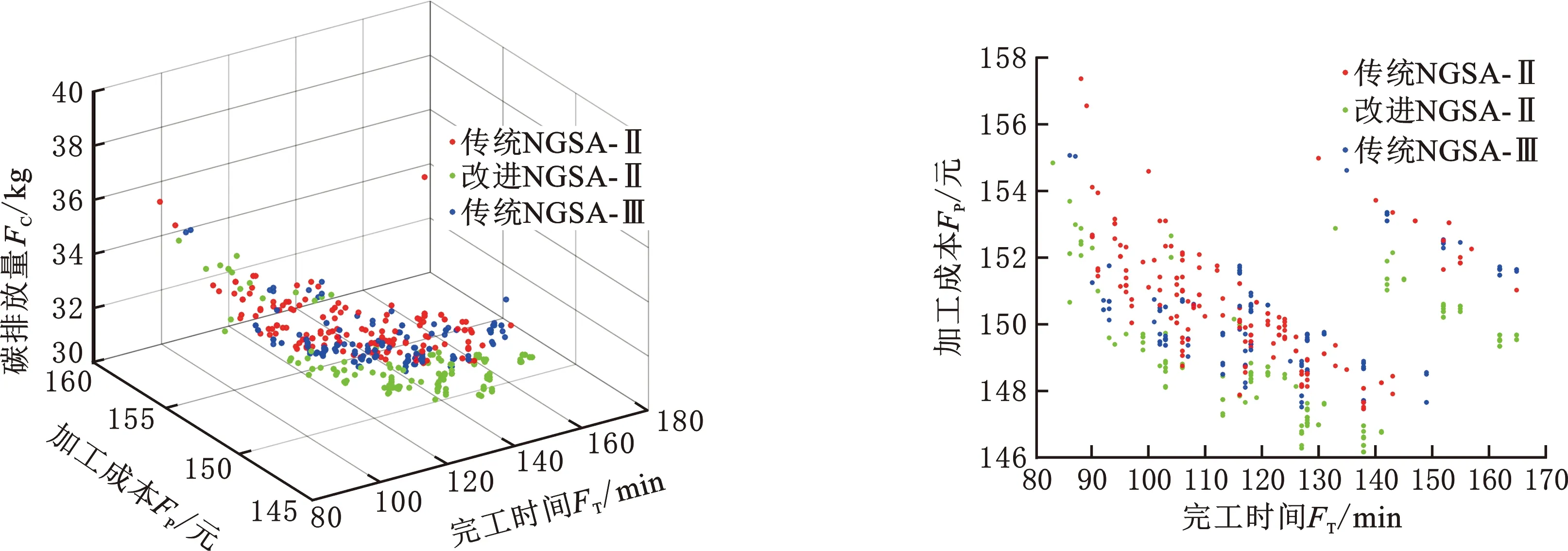
其中，X、Y为两个待比较的非支配解集；x、y为X、Y中的个体；“x≻y||x=y”表示x支配y或x与y相等；Cov(X，Y)表示解集Y中被解集X中至少一个解支配或等同的个体在Y中的占比。当Cov(X，Y)=1时，表明Y中的所有个体都能在X中找到支配或等于它的个体；反之，当Cov(X，Y)=0时，表明Y中的所有个体都不被X中的个体支配。由于Cov(X，Y)与Cov(Y，X)之间不存在必然的联系，故必须同时考虑。若Cov(X，Y)>Cov(Y，X)，则说明解集X对解集Y中个体的支配程度强于解集Y对解集X中个体的支配程度，若Cov(X，Y)

Spacing指标可以反映非支配解集中个体分布的均匀性，其具体定义如下：

(30)

HV指标可以综合反映算法的收敛性与多样性，其具体定义如下：

(31)

其中，δ表示Lebesgue测度，用于测量体积；N为非支配解集大小；vl表示参考点与解集中第l个个体构成的超体积。HV指标越大，说明算法综合性能越好。其中，参考点要被非支配解集中的所有个体支配，本文选择各优化目标函数值中的最大值所对应的点作为HV指标中的参考点。

3.2 参数设置

改进NSGA-Ⅱ中的影响参数有种群规模N、遗传代数G以及AHP中各目标的相对重要度。本文选择遗传算法中几种常用的N与G设置，以中等规模案例MK04为对象，将算法随机运算10次，得到各评价指标均值，见表4。可以发现当N=400，G=200时，Spacing指标效果最好；N=200，G=100时，HV指标效果最好。考虑到种群规模与遗传代数过大时会增加运算成本，种群规模与遗传代数过小时算法性能无可避免地会降低，并且随着遗传代数的增加，种群的进化会逐渐放缓，本文取种群规模N=200，遗传代数G=100。

表4 不同种群规模与遗传代数下MK04案例的对比结果

根据文献[30]及相关专家意见，针对本文调度模型的3个优化目标(最长完工时间f1、加工成本f2、碳排放量f3)，取对应的相对重要度f12=1/2，f13=3，f23=5，f21=2，f31=1/3，f32=1/5。

传统NSGA-Ⅱ算法与NSGA-Ⅲ算法的初始种群均采用随机生成，取交叉率0.9，变异率0.1，NSGA-Ⅲ算法所需的参考点由Deb and Jain方法[31]生成。

3.3 算法比较与讨论

将3种算法在参数一致的前提下各随机运算10次，记录其中最好的指标结果，见表5，其中Cov1为传统NSGA-Ⅱ与改进NSGA-Ⅱ之间的Cov指标，Cov2为NSGA-Ⅲ与改进NSGA-Ⅱ之间的Cov指标，加粗数值为相同算例中较好的结果。

表5 BRdata算例的算法性能对比

由对比结果可知，在COV指标方面，改进NSGA-Ⅱ在10个算例上均大幅优于另外两种算法，说明本文算法求得解集中几乎所有个体都不会被对比算法求得的解支配，解的质量更优，算法的寻优能力较强；在Spacing指标方面，改进NSGA-Ⅱ在算例MK06和MK09上略劣于另外两种算法取得的最优值，但在其余算例上均优于对比算法；在HV指标方面，改进NSGA-Ⅱ仅在算例MK01上略劣于NSGA-Ⅲ所取得的最优值，但在另外9个算例上均表现更好。以MK01、MK06和MK09算例为对象，绘制HV指标和Spacing指标的对比箱型图，对比结果如图4所示。

(a)MK01算例Spacing指标 (b)MK01算例HV指标

从图4可以看出，本文算法虽然未能同时在这3个算例上取得评价指标的最优值，但箱型图上下限之间的距离更短，整体分布更为集中，也更接近最优值，说明10次对比实验中本文算法求得的解集在Spacing指标与HV指标方面的差异较小，求解稳定性较强，并且解集的各评价指标都较为优秀，进而说明本文算法在收敛性、均匀性及多样性方面比对比算法更优。

将3种算法在不同规模的算例MK01、MK03、MK10上各随机运行一次后，绘制各优化目标值的收敛曲线，如图5～图7所示。可以看出，在3个算例中，本文算法均取得了各优化目标的最优初始值，并且各优化目标的收敛速度和收敛结果均优于另外两种对比算法，结合HV指标的对比结果可知本文算法在收敛性方面表现较为优秀。分析其主要原因如下：

(a)最长完工时间 (b)加工成本 (c)碳排放量

(a)最长完工时间 (b)加工成本 (c)碳排放量

(a)最长完工时间 (b)加工成本 (c)碳排放量

(1)基于AHP的贪婪解码策略对初始种群的多个目标进行了协同优化，避免了种群质量朝着某一个目标方向偏移，从而使得初始种群在各目标维度上都优于对比算法，在一定程度上加快了算法收敛。

(2)自适应的遗传算子使得算法在迭代初期能够以较大交叉率、变异率加快种群进化，并在迭代后期通过减小交叉、变异率以减少对优质个体的破坏，加快算法的收敛。

(3)改进的精英保留策略通过提高算法后期被支配个体被保留的概率，为种群添加了多样的基因，降低了算法收敛于局部最优的可能性。

记录迭代过程中种群的个体重复率，即重复个体在种群中的占比，包括决策向量重复(个体之间的基因组成相同)和目标向量重复(个体之间的基因组成不同但表现形式相同)，并绘制图8所示的重复率迭代折线图。

从图8可以看出，在同一个算例中，随着算法的迭代，个体重复率逐渐增加，并且在较大规模的算例中，出现重复个体的概率也相对较低，而本文算法求得解集中的个体重复率及个体重复率的增长速度要明显低于对比算法。结合Spacing指标与HV指标的对比结果可知，本文算法求解的多样性与分布性更好。其主要原因如下：

(a)MK01算例 (b)MK03算例 (c)MK09算例

(1)种群初始化中通过Tent混沌映射来进行个体的生成，减少了个体之间的相似性，使种群尽可能均匀的分布到解空间，进而提高了种群的多样性。

(2)自适应的遗传策略在进化初期及种群非支配等级数量较少时提高了交叉、变异率，在促进新个体的产生同时减少了重复个体的产生。

(3)改进的精英保留策略为每个个体分配了自适应的被保留概率，从而为种群添加了不同非支配等级的个体，在很大程度上增加了种群多样性。重复个体由于互不支配而具有了相同的非支配等级，而传统NSGA-Ⅱ与NSGA-Ⅲ都是先按照非支配等级来保留个体，容易保留非支配等级较低的重复个体，虽然NSGA-Ⅲ引入了基于参考点的方式来增加种群多样性，但仅用于选择最后一个非支配等级(即保留了该非支配等级的个体后，种群个体数不小于N)，一般适用于收敛困难的高维和超高维空间，在本文研究的问题中优势并不明显。同时外部存档策略又能有效避免多样化的个体对种群整体质量的影响，较好地平衡了算法收敛与多样化的能力。

为进一步验证本文算法在实际问题中的有效性，以某电梯零部件制造企业金工车间的一个加工任务为例，将其数据整理简化成一个8×6(8个工件，6台设备)的生成调度问题，具体的加工数据见表6，其余数据与BRdata算例中一致，将每种算法各随机运算10次，图9为各优化目标函数值的箱型图，相应的指标对比结果见表7，其中Cov1表示传统NSGA-Ⅱ与改进NSGA-Ⅱ的解集之间的支配关系，Cov2表示NSGA-Ⅲ与改进NSGA-Ⅱ的解集之间的支配关系。

表6 简化整理后的8×6柔性作业车间调度任务实例

(a)最长完工时间箱型图 (b)加工成本箱型图 (c)碳排放量箱型图

由表7可以发现，本文算法在3个优化目标上均取得了最优值与均值，说明其寻优能力要优于传统NSGA-Ⅱ与NSGA-Ⅲ。图9a与图9b中箱型图分布范围相较于传统NSGA-Ⅱ与NSGA-Ⅲ而言优势不够明显，图9c中箱型图分布范围比另外两种算法更小，说明本文算法在优化最长完工时间与加工成本的稳定性与收敛性上优势不够明显，在求解碳排放量时的稳定性与收敛性较强。除此之外，Cov指标、Spacing指标及HV指标相对另外两种算法而言更优。

表7 实际算例算法性能比较

为了更直观地分析三种算法在求解本文调度问题结果上的差异，各随机运算1次后得到在最长完工时间、加工成本与碳排放量3个目标维度上的Pareto前沿面分布图，如图10所示。

(a)原始视图 (b)完工时间-加工成本视图

由图10a可以看出，本文调度问题的解集是由一系列分布在Pareto最优面周围的离散解组成的，改进NSGA-Ⅱ求得各优化目标函数值在整体上要优于对比算法。由图10b和图10d可以看出，在相同的完工时间下，相比传统NSGA-Ⅱ和NSGA-Ⅲ，本文算法得到解的加工成本和碳排放量更低也更收敛，并且整体上随着完工时间的增加而减少。由图10c可以看出，随着加工成本的增加，碳排放量呈增长趋势，但在相同加工成本下本文算法求得解的碳排放量更低。综上所述，在相同的运算条件下，本文算法得到的解在各目标维度上的质量更优。

4 结语

(1)本文考虑设备能耗、刀具磨损及切削液消耗在生产过程中造成的碳排放以及加工过程中产生的能耗、人工费用，建立了以最小化碳排放量、最长完工时间和加工成本为目标的低碳调度模型。

(2)针对研究问题的特点，设计了一种改进NSGA-Ⅱ进行求解，通过Tent混沌映射与融合AHP的贪婪解码的策略形成质量较高的初始种群；设计了一种自适应遗传策略，根据进化阶段与种群非支配状态动态调整交叉率、变异率；对传统精英保留策略进行改进，提高了种群多样性，并通过外部存档策略保留优质个体。

(3)基于经典调度算例BRdata进行了扩展，与传统NSGA-Ⅱ与NSGA-Ⅲ的对比证明了本文算法在种群初始化与收敛性等方面的优势，并通过一个实际案例验证了本文算法求解多目标柔性作业车间低碳调度问题的有效性。

后续研究考虑把低碳调度问题扩展到更为复杂的生产系统中，如动态生产环境等，并添加更多的实际约束，更贴近实际生产，同时进一步提高算法的通用性。