基于旋转周期解的星型网络同步问题
祝熙娟, 王 帅
(长春理工大学 数学与统计学院, 长春 130022)
0 引 言
复杂网络的同步现象在物理、 生物、 化学模型中普遍存在[1]. 复杂网络的同步受多种因素影响, 如网络拓扑结构、 振子本身的动力学以及振子的参数等. 网络的拓扑结构对同步有极大影响. 例如: Pecora等[2]研究了网络结构对称性与同步之间的联系, 发现簇同步模式的存在取决于网络拓扑的对称性, 而出现簇同步模式取决于相应解的稳定性; Zheng等[3]研究了周期同步振子的网络结构对同步的影响; Wang等[4]研究了当振子参数不相同时系统的同步情况, 发现只有当振子的对称节点参数相同时, 才会产生簇同步; 文献[5]研究表明, 多种网络模型具有对称性. 星型网络是一种特殊的网络拓扑结构, 其具有一个中心节点及多种类型的对称性. Xu等[6]描述了相位振子在星型网络中的同步机制; Lacerda等[7]研究了在非相同振子星型网络中的远程同步.
旋转周期解理论利用旋转周期矩阵Q衡量网络拓扑结构的几何性质, 能用一种统一的方法解释系统多种类型的同步性和多种复杂的动力学行为.本文用旋转周期解理论研究星型网络中耦合振子的同步现象[8-9].首先, 考虑一个旋转周期动力学系统:
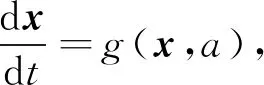
(1)
其中:x(t)∈2n;a∈[0,1];g:2n×1→2n为C2连续的,g(x,a)=Qg(Q-1x,a),Q是2n×2n的正交矩阵,g(0,a)=0.如果系统(1)有x(t+T)=Qx(t)形式的解, 则称这种解为系统(1)的旋转周期解.g(x,a)=Qg(Q-1x,a)称为旋转周期条件,Q称为旋转周期矩阵[10-11].本文研究范德波尔振子网络的星形拓扑结构对同步的影响.
1 模型简介
考虑用如下范德波尔振子描述节点动力学模型[12]:
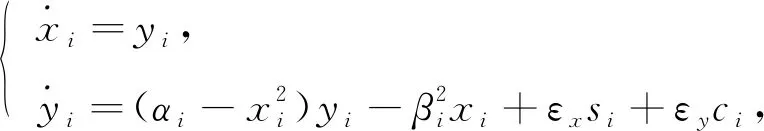
(2)
其中:
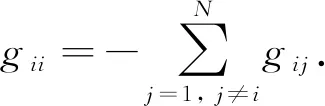
本文研究中心节点与N个等长节点链耦合的星型网络.图1为一个与中心节点连接的具有3条射线, 每条射线上有2个振子的扩展类星型网络, 并且每个振子都符合范德波尔网络模型.

图1 七振子星型网络示意图
方程(2)可以写成如下格式:

(3)
其中A为振子本身的线性项矩阵,f(X)为所有振子高阶项组成的向量,eG为系统的Laplace矩阵(e表示振子的耦合强度, 即式(2)中的εx和εy), 矩阵A和eG的具体形式为
为表述方便, 下面用H表示A+eG.
2 理论分析
2.1 旋转周期解
考虑完全相同振子与非完全相同振子的同步情况.首先找出满足F(X)=QF(Q-1X)的Q, 找到的所有Q形成一个群S.网络对称性均可用置换矩阵Q描述, 该矩阵以一种保持动力学方程不变的方式对节点进行重新排序.为判断系统的同步情况, 先用下列算法将H和Q同时对角化.
算法1
步骤1) 先将Q对角化. 利用M-1QM=Q1得到对角化后的Q1(仍用Q表示):
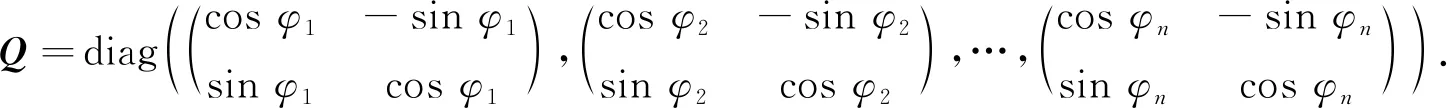
(4)
步骤2) 重新调整对角化后的Q, 并将Q中相同的特征值调整到一起, 调整后的Q变为
对应Q的调整, 调整M的特征向量, 得到调整后的M1(仍用M表示).
步骤3) 利用M-1HM=H1得到一个对角块矩阵, 设为
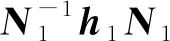
步骤4) 由M×N得到的矩阵可以将H和Q同时对角化.
同时对角化后的Q形式如式(4), 其中φi≠0(i=1,2,…,n)(φi=0等于φi=2π); 对角化后H的形式如下(对角化后的Q和H仍用Q和H表示):
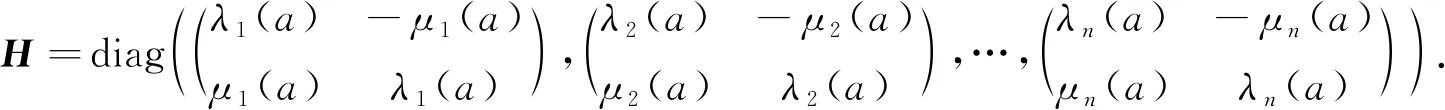
(5)
本文将同步解的分岔问题转化为旋转周期解的分岔问题, 下述定理讨论了同步解的存在性.
定理1[13]假设(x=0,y=0,a=0)是系统(3)的临界点, 设对角化后的Q和H形式分别如式(4)和式(5)所示, 并假设满足下列条件:
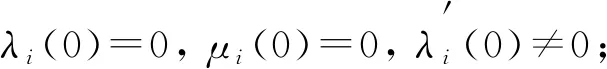
2) 对i=1,2,…,7, 有μi(0)≠0.
则(x=0,y=0,a=0)是系统(3)中旋转周期解的一个分岔点.
由定理1可得系统同步存在的临界条件——旋转周期解的分岔点.下面引入能判断网络拓扑结构与同步之间关系的定理.
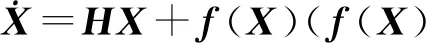
H=diag(λ1±ω1i,λ2±ω2i,…,λn±ωni).
则有:
1) 当ω1=ω2=…=ωn并且φ1=φ2=…=φn时, 系统具有完全同步解;
2) 当ω1=ω2=…=ωn并且φ1=φ2=…=φn/2=c,φn/2+1=φn/2+2=…φn=c+π时, 系统具有反向同步解;
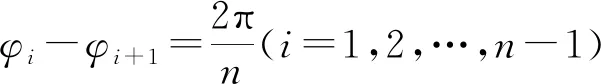
4) 当φ1,φ2,…,φn被分成k组, 在同一组中满足ωk1=ωk2=…=ωkm和φk1=φk2=…=φkm(这里km表示第k组中的第m个振子)时, 系统有簇同步解.
在星型网络中, 满足旋转周期条件的所有旋转矩阵Q形成不同的群.利用这些群的共轭类, 可得到所有不同类型的同步解[7].通过上述算法, 可将Q和H同时对角化, 并由Q和H的特征值判断网络相应的同步情况, 但相同形式的Q可能得到不同形式的同步解.
2.2 完全相同振子的同步
当振子完全相同时, 网络的对称性保持不变.先验证满足QH=HQ的所有Q:
由Q1~Q6可组成一个群S, 群S中可有多个不同的共轭类.设群S中的共轭类为Rq(q=1,2,3),Rq中不同的q表示不同的同步类型, 其中Q是由系统不同变换形式得到的旋转矩阵.R1={Q1},Q1是单位矩阵.在图1中, 将振子2,4,6的位置进行循环变换(相应的振子3,5,7也会相应变换), 可得Q2.同理也可得Q3.从而可设R2为振子通过循环变换得到的, 则R2={Q2,Q3}.
当(2,4,6)→(4,6,2)时, 变换结果如图2所示, 该网络的对称性对应于群R2中的Q2.通过对称变换, 分别将振子2,3和振子4,5位置互换, 可得Q4.同理可得Q5,Q6.从而可设R3={Q4,Q5,Q6}.当(2,3,4,5)→(4,5,2,3)时, 变换结果如图3所示, 该网络的对称性对应于群R3中的Q4.

图2 振子循环变换结果

图3 振子对称变换结果
根据定理2, 该网络的同步类型与Q的特征值有关, 可以验证R1,R2,R3构成一个群, 每个共轭类中Q的特征值都相同, 因此同一共轭类对应于相同类型的同步解.对角化后,R1中矩阵的特征值为(1,1,1,1,1,1,1).由定理2可知, 该系统具有完全同步解.R2中矩阵的特征值为

(6)
该系统具有周期同步解.R3中矩阵的特征值为(-1,-1,1,1,1,1,1), 该系统具有部分反向同步解(因为系统中只有一部分振子满足定理2中反向同步的情况, 因此称其为部分反相同步解).完全相同振子的星型网络中具有完全同步、 周期同步和部分反向同步3种类型的同步解.表1列出了完全相同振子的同步情况.

表1 完全相同振子同步情况
2.3 非完全相同振子的同步
通过设置参数可使振子不完全相同, 下面讨论非完全相同振子的同步情况. 设当振子参数相同时, 可用相同的字母符号代替. 例如, 若系统满足射线上振子同步, 则振子2,3设为相同参数b, 振子4,5设为相同参数c, 振子6,7设为相同参数d, 则系统振子参数的情况为(a,b,b,c,c,d,d).此时验证的旋转矩阵Q只有单位矩阵Q1一种情况.对角化后的特征值为(1,1,1,1,1,1,1).此时只有部分同步解.当振子参数的情况为(a,b,c,b,c,b,c)时, 满足QH=HQ的Q有Q2,Q3.此时验证的旋转矩阵有Q2,Q3两种情况.对角化后的特征值为式(6).根据定理2, 系统有周期同步解.当振子参数的情况为(a,b,c,b,c,d,e), (a,b,c,d,e,b,c)或(a,d,e,b,c,b,c)时, 满足QH=HQ的Q有Q4,Q5,Q6.此时验证的旋转矩阵有Q4,Q5,Q6三种情况.对角化后的特征值为(-1,-1,1,1,1,1,1), 此时系统有部分反向同步解.表2列出了非完全相同振子同步的情况.由表2可见, 当系统是非完全相同振子时, 只能得到三种不同类型的同步解.当同步情况为(a,b,b,c,c,d,d)时, 系统可得到部分同步解; 当同步情况为(a,b,c,b,c,b,c)时, 系统可得到周期同步解; 当同步情况为(a,b,c,b,c,d,e), (a,b,c,d,e,b,c)或(a,d,e,b,c,b,c)时, 系统可得到部分反向同步解.

表2 非完全相同振子同步情况
3 数值模拟
3.1 完全相同振子的数值模拟
取所有振子的分岔参数βi=4(i=1,2,…,7), 固有频率αi=1(i=1,2,…,7).图4为完全相同振子的3种同步类型.
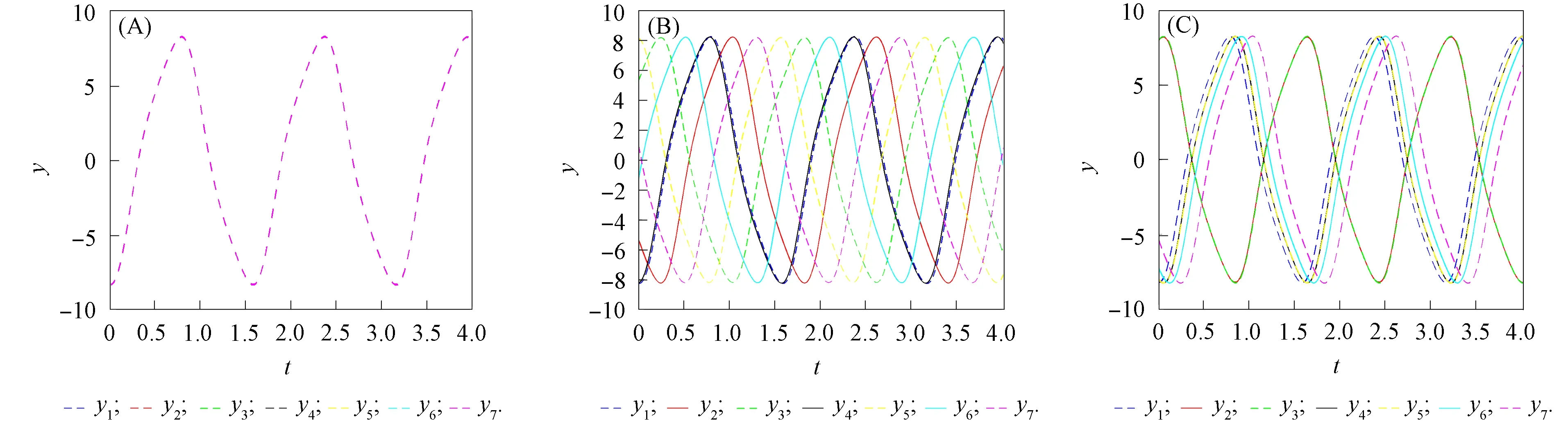
图4 完全相同振子的3种同步类型
在R1中, 取耦合强度εx=0.01,εy=0.01, 则对角化后的Q和H(对角化后Q*和H*仍用Q和H代替)分别为
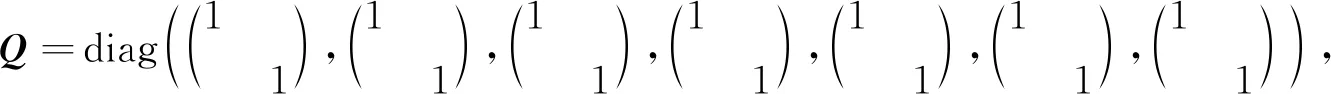
(7)
可知对角化后Q的所有特征值都相等, 由于有误差, 对角化后H的特征值相似, 因此根据定理1, 此时系统具有完全同步解.由图4(A)可见, 振子y1,y2,…,y7的轨迹完全重合, 可知此时系统所有振子是完全同步的.
在R2中, 取耦合强度εx=0.01,εy=0.01, 则对角化后的Q和H分别为
可知对角化后Q的特征值中有两对特征值具有相位差, 对角化后H的特征值中对应相位差相等.根据定理1, 此时系统具有周期同步解.由图4(B)可见, 振子y2,y4,y6和振子y3,y5,y7的轨迹具有相位差, 可知此时系统中振子2,y4,y6和振子y3,y5,y7分别是周期同步的.
在R3中, 取耦合强度εx=0.01,εy=0.01, 则对角化后的Q和H分别为

(9)
可知对角化后Q的特征值中有两对具有相位差, 对角化后H的特征值中对应相位差相等.根据定理1, 此时系统具有部分反向同步解.由图4(C)可见, 振子y2,y4和振子y3,y5的轨迹具有相位差, 可知此时系统中振子y2,y4和振子y3,y5分别是部分反向同步的.
3.2 非完全相同振子的数值模拟
取所有振子的固有频率αi=1(i=1,2,…,7).图5为非完全相同振子的3种同步类型.

图5 非完全相同振子的3种同步类型
在R1中, 设各振子的分岔参数分别为β1=6,β2=β3=4,β4=β5=7,β6=β7=9, 此时系统每条射线上的振子参数相同, 取耦合强度εx=εy=0.001, 则对角化后的Q为式(7), 对角化后的H为
可知对角化后Q的所有特征值都相等, 对角化后H有三对相等的特征值.根据定理1, 此时系统具有部分同步解.由图5(A)可见, 振子y2和y3、 振子y4和y5、 振子y6和y7的轨迹分别重合, 可知系统中振子y2和y3、 振子y4和y5、 振子y6和y7分别是部分同步的.对于系统中每条射线上彼此同步的情况, 也称为射线同步.
在R2中, 设振子的分岔参数分别为β1=6,β2=β4=β6=4,β3=β5=β7=8,εx=εy=0.01, 则对角化后的Q为式(8), 对角化后的H为
可知对角化后Q的特征值中有两对具有相位差, 对角化后H的特征值中对应相位差相等.根据定理1, 可知此时系统具有周期同步解.由图5(B)可见, 振子y2,y4,y6和振子y3,y5,y7的轨迹分别具有相位差, 可知系统中振子y2,y4,y6和振子y3,y5,y7分别是周期同步的.
在R3中, 设各振子的分岔参数分别为β1=6,β2=β4=5,β3=β5=3.5,β6=4,β7=4.5, 耦合强度εx=εy=0.01, 则对角化后的Q为式(9), 对角化后的H为
可知对角化后Q的特征值中有两对具有相位差, 对角化后H的特征值中对应相位差相等.根据定理2, 此时系统具有部分反向同步解.由图5(C)可见, 振子y2和y4、 振子y3和y5的轨迹分别具有相位差, 可知此时系统中振子y2和y4、 振子y3和y5分别是部分反向同步的.
综上所述, 本文研究了由7个范德波尔振子组成的星型网络的同步现象, 利用旋转周期解理论讨论了星型网络模型的同步现象以及系统具有完全相同或者非完全相同振子时系统的同步情况.首先找到旋转矩阵Q, 所有满足F(X)=QF(Q-1X)的旋转矩阵组成一个群, 然后对Q进行分类, 将相同类型的Q组成一个群的共轭类, 不同类型的Q得到不同的共轭类; 然后利用这些群的共轭类和对角化方法, 给出不同类型的同步现象.本文以三射线内外双层七振子为例研究了网络的同步情况.结果表明: 当系统具有完全相同振子时, 可得到完全同步、 周期同步和部分反向同步3种不同类型的同步解; 当系统具有非完全相同振子时, 可得到部分同步、 周期同步、 部分反向同步3种不同类型的同步解; 系统在上述两种情况下, 均出现了周期同步和部分反向同步.本文基于旋转周期解理论, 研究了范德波尔振子组成的星型网络, 事实上该方法也可以直接推广到更多条射线或更多层的星型网络或者采用其他阵子的网络模型中.例如: 文献[8]在更一般的条件下给出了3种不同拓扑网络中耦合振子的同步或簇同步机制, 并讨论了网络拓扑结构对同步性的影响; 文献[9]利用惠更斯阵子研究了旋转波的存在性, 并利用旋转周期理论给出了一种判断旋转波类型的基本原理.

