部分线性变系数模型的Liu估计*
安佰玲,卢 琦,马 宁
(淮北师范大学数学科学学院,安徽 淮北 235000)
1 问题的提出
部分线性变系数模型是变系数模型和部分线性模型的推广.这类模型一般可记为
(1)
其中:yi为因变量观察值;xi=(xi1,xi2,…,xip)T,zi=(zi1,zi2,…,ziq)T,为对应自变量的观测值;β=(β1,β2,…,βq)T,为q维未知待估参数;α(·)=(α1(·),α2(·),…,αp(·))T,为未知非参数函数系数;模型误差εi相互独立,且E(εi)=0,Var(εi)=σ2.
模型(1)的参数分量β的估计一直是研究的热点.Zhang等[1]利用局部多项式方法估计了模型(1);Xia等[2]基于局部线性方法提出了一种新的有效估计;Zhou等[3]基于小波方法估计了部分线性模型的参数和非参数;Fan等[4]对半参数变系数模型中的β进行了Profile最小二乘估计,并讨论了估计的渐进性质;Wei等[5]对部分线性可加模型中的β进行了Profile最小二乘估计,并讨论了估计的渐进性质.这些研究成果多数假定模型中的自变量不存在多重共线性,但在实际问题中经常会遇到自变量之间存在近似的线性关系.多重共线性会导致回归系数的估计值或标准差估计值异常偏大,回归系数估计值的符号与现实意义相违背等问题.解决这类问题较成熟且有效的方法是构建有偏估计,有偏估计通过牺牲无偏性获得较小的均方方差,如岭估计和主成分估计.Liu[6]结合岭估计和stein估计的优点提出了一种有偏估计(Liu估计).此后,越来越多的学者将Liu估计理论应用于广受关注的半参数模型.例如,Akdeniz等[7-8]结合Backfitting算法和Speckman方法给出了半参数回归模型下的Liu型估计;Wei等[9]研究了半参数可加模型下的Liu估计和约束Liu估计.笔者拟结合文献[10-15]并基于Profile最小二乘方法和Liu估计法,构造β的Profile-Liu估计和剖面最小二乘广义Liu估计,在均方误差标准下研究这2个估计量的性质.
2 参数分量Liu型估计的构造
2.1 加权最小二乘估计
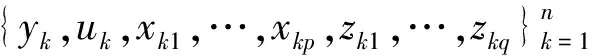
(2)
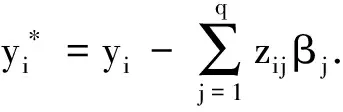
为了叙述方便,引入以下记号:
ε=(ε1,ε2,…,εn)T,Wu0=diag(Kh(u1-u0),Kh(u2-u0),…,Kh(un-u0)),
于是模型(2)可表示为
Y-Zβ=M+ε,
(3)
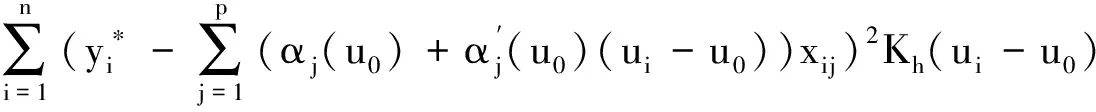
(4)
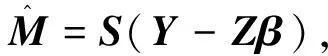
2.2 Profile-Liu估计
将M的估计代入(3)式替换其中的M,整理可得如下线性回归模型:
(5)
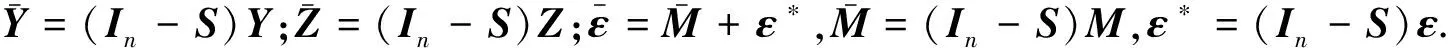
(6)

(7)
由(7)式中的目标函数对向量β求导并令其为0,可求得
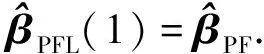
2.3 剖面最小二乘广义Liu估计
Hoerl等[12]将线性模型岭估计中的参数k扩展到参数矩阵K,获得广义岭估计;Akdeniz等[13]将线性模型Liu估计中的参数d扩展到参数矩阵D,获得广义Liu估计.在此启发下,笔者获得了部分线性变系数模型的广义Liu估计.
设D=diag(d1,d2,…,dq),di>0,令
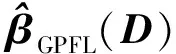
3 估计的理论性质
3.1 估计量优劣性的判定标准
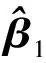
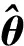
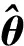
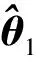
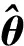
3.2 Profile-Liu估计的性质
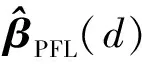
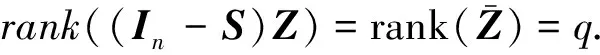

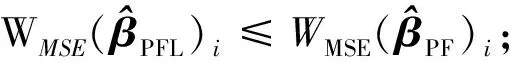
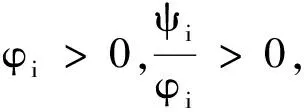
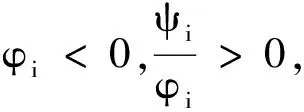
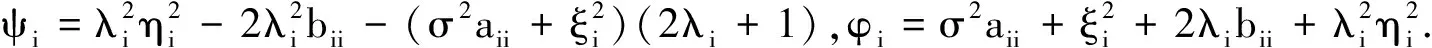
证明因为
所以
(8)
(9)
其中
根据引理1,整理(8),(9)式可得
(10)
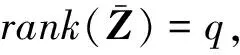
于是
(11)
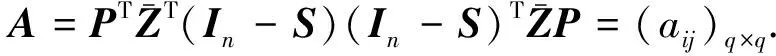
(12)
其中ηi=(PTβ)i;
(13)
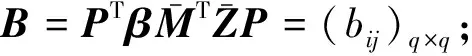
(14)
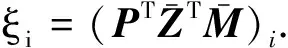
(15)
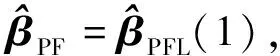
(16)
于是由(15),(16)式,可得
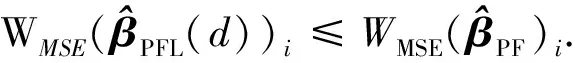

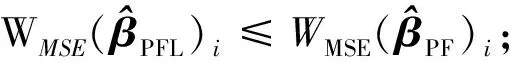
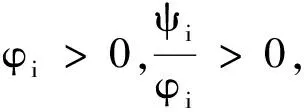
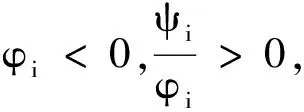
证毕.
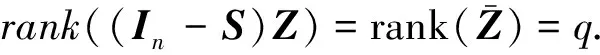
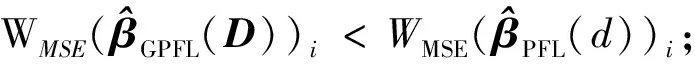

其中
证明事实上,

于是
(17)
(18)
由定理1的证明过程并结合(17),(18)式,可得



