充填法开采地表移动带内建(构)筑物稳定性模拟研究

栾伟杰,李海基,徐厚臻,张 超

(1.山东黄金矿业(莱州)有限公司焦家金矿,山东 烟台 261400;2.北京科技大学土木与资源工程学院,北京 100083)

1 前言

地下矿床开采引起岩体变形并造成建(构)筑物破坏的问题,在我国乃至世界上都引起了社会的广泛关注[1-2]。在地下开采过程中,矿产资源被大量采出后开采区域周围的矿、岩体原有的平衡状态受到破坏,地下岩体内的应力发生重新分布,形成新的平衡,在这过程中上覆岩层将可能发生冒落、断裂、弯曲、沉降等现象,最终可能波及地表,甚至在开采区域上方造成大面积的塌陷[3-4]。因此,为最大限度地减少岩体变形移动产生的影响,需要在准确分析矿山实际情况前提下,对开采区域进行全面、准确的预测,实现建(构)筑物的稳定性分析,并提出相应的措施方法是十分必要的。

在进行地表建(构)筑物稳定性分析方面,主要有理论分析、相似实验、数值模拟、现场监测等几种研究方法[5]。程立年等[6]运用概率积分法理论计算出的矿山安全开采深度,并计算最大爆破安全允许距离从而实现某金矿大断裂带构造条件下地表稳定性分析。刘建博[7]、曹文龙[8]等采用数值模拟实现了对矿体充填法开采井筒稳定性分析,实现了地表岩层移动和影响范围的仿真模拟分析与研究。张超等[9]综合应用理论分析和数值模拟耦合实现充填法开采建(构)筑物稳定性分析及回采优化研究。Li[10]和蒯洋[11]等通过布置合理的监测系统实时进行矿体开采条件下建(构)筑物的变形分析,并结合理论分析对地表变形实现预测研究。除此之外,Chomacki 等[12]采用人工智能的方法,使用贝叶斯分类器和贝叶斯网格构建损伤风险评估模型,最终实现对地下采矿过程中建筑物的风险受损分析。

综合对比以上的研究方法,数值模拟研究由于其时间成本低、实验研究少、应用范围广等优点已广泛应用于矿山各方面的研究中[13-15]。本文综合前人的研究成果,应用有限差分软件FLAC3D构建矿区精细化三维模型,进行地表移动带内建(构)筑物稳定性分析,并结合安全性分析综合讨论,为矿山安全现状评价以及合理开采优化提供理论依据。

2 工程概况

山东黄金焦家金矿某矿区目前矿山采用上向水平分层尾砂胶结充填法与上向进路式胶结充填法进行开采。现阶段-430 m 水平以上的矿体已基本采空,并全部进行充填治理,经相关机构评估分析矿区浅部已不存在对地表造成重大安全隐患的采空区。后续设计开采区域为主要为Ⅰ号矿体,设计中段-470 m、-510 m、-550 m、-590 m、-630 m,首采中段为东矿区-470 m、-510 m 中段。矿区自上而下分中段开采,中段开采顺序为自风井向提升井后退式回采。平行矿体回采,根据实际情况采取先回采上盘矿体,再回采下盘矿体,上盘矿块超前下盘矿块一定安全距离予以回采。

以上下盘岩石移动角70°、侧翼移动角75°进行矿区地表移动带圈定,在移动带内存在新南风井、地表餐厅及办公楼等重要建(构)筑物,且新南风井距离移动带边界12 m,地表餐厅及办公楼距离移动带边界214 m,具体如图1所示。其中新南风井位于矿体下盘,井口标高+65 m,井底标高-430 m,以75°圈定的保安矿柱。根据《有色金属采矿设计规范》,矿区内新南风井井筒、地表主要建(构)筑物不允许出现变形破坏现象;因特殊原因需布置在移动范围保护带内时,应留设保安矿柱。因此需要分析矿区开采对地表主要建(构)筑物稳定性的影响,并对开采区域围岩稳定性、变形规律进行分析。

图1 地表移动带分布及主要监测点布置

3 三维模型构建

FLAC3D广泛应用于土木、交通、采矿、水利等行业,可实现对岩石、岩土和支护结构等建立高级三维模型,进而完成复杂的工程数值分析。为合理的分析开采和充填过程中建(构)筑物的稳定性,本次采用FLAC3D软件进行矿体开采充填过程的三维数值计算,通过模拟实际开采状况对建(构)筑物进行精确分析[16]。

本文前期应用3D Mine 进行矿区三维模型的构建,将模型导入Rhinoceros 中进行优化,借助Griddle工具进行模型的网格划分,并生成.f3grid 文件,为后期三维数值模拟提供模型基础,并借助Tecplot360 实现分析结果的后期处理。

3.1 模型区域构建

在矿山工程中,采矿本身是一个复杂的力学过程,其中包含许多不确定因素的影响,又由于数值模拟的定量结果一般仅作评价的应用。因此在模拟的过程中,不刻意寻求力学模型和本构关系的精密,即不要求所建立的力学模型过于复杂,只需能反映出岩体的基本力学特性及矿山开采的基本过程。借助望儿山矿区提供的基本资料,进行矿区三维模型的构建。使用自由三角形网格进行模型剖分,在矿体和井筒处网格进行加密,其他区域适当增大网格尺寸。模型设计尺寸长1 082 m、宽1 600 m、高840 m,模型共计网格节点数333 224 个,网格单元1 989 366 个。设置摩尔-库仑准则作为围岩、矿体的本构模型,空模型作为矿体开采本构模型[20]。模型具体分布位置如图2所示。

图2 三维模型构建

3.2 边界条件施加及初始平衡

在应力场中将模型的边界条件设定为:采用快速应力边界法(S-B 法)进行初始应力场生成,该方法仅在模型表面是将应力场,对边界速度不做处理,使边界速度处于自由状态。最后通过模型到达平衡后将所有节点速度清零的方式模拟在初始条件下的平衡状态。

模型中使用的基本力学参数见表1,按照式(1)进行初始应力的施加,最终模型达到平衡后得到最大主应力为43.5 MPa,最小主应力为28.22 MPa,垂直应力为28.2 MPa,与式(1)计算结果误差较小,模型初始平衡过程较为准确。

表1 基本力学试验参数

3.3 开采顺序设计及监测点布置

结合矿山实际生产情况,设计三步骤开采矿体,其中一步骤开采-430 m 以上矿体,该区域内矿体前期已基本开采完毕并进行充填治理;二步骤作为后续设计开采的首采区域,开采水平为- 430～-510 m,主要包括-470 m 中段、-510 m 中段;三步骤主要开采-510～-650 m 水平矿体,主要包括-550 m 中段、-590 m 中段、-630 m 中段。待模型初始平衡后迭代进行后续开采分析,设计各区域矿体开挖500 步后进行充填处理,充填阶段设计计算步数为3 000 步,持续进行,直至矿体开采结束。

为进行所研究区域稳定性监测,分别对新南风井、地表餐厅及办公楼进行设置监测点进行变形监测,井筒壁上间隔25 m 布置监测点,共布置20 个监测点;地表餐厅及办公楼附近等距设置监测点,共布置17 个监测点。

4 模拟结果分析

本节主要从位移变形、应力变形和塑性区变化三方面进行模拟结果分析,综合考虑对开采过程中建(构)筑物稳定性进行综合评判。

4.1 位移变形分析

为准确分析新南风井周围的位移变形量,选取井筒与矿体之间构建A-A 剖面,具体如图3所示。一步骤开采结束后地表的垂直变形最大值为11.1 mm,最大变形值位置为开采矿体正上方,向四周逐渐减小至未扰动区域。观察新南风井与开采扰动区之间的关系,可以看出该建筑物区域垂直Z 方向井筒位于扰动边界以外153 m;二步骤开采结束后地表的垂直变形最大值为17.1 mm,井筒位于扰动范围边界以外62 m;三步骤开采结束后地表的垂直变形最大值为33.9 mm,井筒位于扰动范围边界以外16 m,虽然相比于前二步骤有较大幅度的减小,但依旧处于较大扰动范围外,因此认为矿体开采不会对新南风井、地表主要建(构)筑物产生下沉破坏。

图3 各步骤开采结束后模型下沉变形

对新南风井井筒的变形监测点进行统计分析,并参考各步骤结束后井筒具体位置变形情况,绘制井筒变形分布图,具体如图4所示。可以看出在各步骤矿体开采过程中井筒周围的变形均是呈现先小幅度变化后趋于稳定的变化规律,三步骤结束后,井筒的最大X 方向变形值为16 mm,最大Y 方向变形值为3 mm,最大Z 方向变形值为20 mm。变形主要集中在井筒端部位置和底部位置,底部位置由于距离矿体较近,产生的变形量相对较大,而端部主要是由于地表垂直变形主导引起的整体较小变形。整体来看,矿体开采对新南风井井筒均未造成较大扰动,井筒始终处于稳定状态,进一步说明圈定的保安矿柱(移动角75°)满足要求。

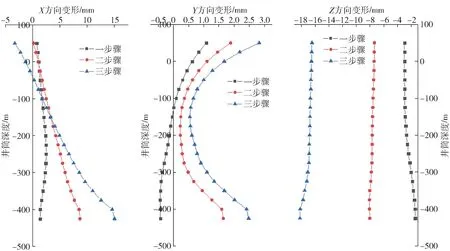
图4 井筒位置变形分布

对地表餐厅及办公楼的变形监测点进行统计分析,变形分析如图5所示。在各步骤矿体开采过程中建筑物周围的变形同样是呈现先小幅度变化后趋于稳定的变化规律,三步骤结束后,地表餐厅及办公楼的最大X 方向变形值为1.5 mm,最大Y 方向变形值为3.5 mm,最大Z 方向变形值为5 mm,变形值属于毫米级,很难造成建(构)筑物的破坏。结合监测点综合进行各步骤结束后地表变形规律分析,具体如图6所示。矿体开采过程中基本上很难对地表餐厅及办公楼产生影响,该建筑物所在区域始终处于稳定状态。因此综合分析认为,进行该矿区矿体开采,使得矿区内地表始终处于稳定状态。

图5 地表主要建(构)筑物监测点变形分析

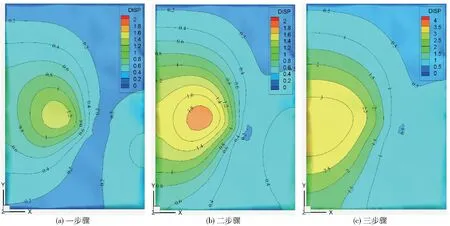
图6 地表位移变形分布

4.2 应力变形分析

进一步结合大小主应力分析矿体开采引起的变形情况,各步骤开采结束后主要剖面的最大、最小主应力云图如图7所示。一步骤开采结束后应力变形仅在矿体附近数十米小范围内,应力集中区域仅在矿体边帮少部分区域,最大主应力可达44 MPa,最小主应力可达21 MPa,远离矿体位置逐步恢复至初始应力状态;与一步骤类似,二步骤开采结束后应力扰动区域也仅局限至开采矿体附近数十米小范围内,最大主应力可达54 MPa,最小主应力可达21 MPa,应力集中区域足以造成围岩的破坏,而在远离采场区域逐渐恢复至初始状态;三步骤开采结束后最大主应力可达61 MPa,最小主应力可达21 MPa。

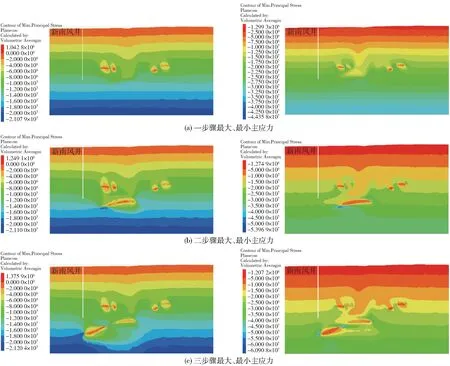
图7 各步骤开采结束后A-A 剖面大、小主应力变形

综合各步骤开采结果可知,矿体开采后应力扰动区域仅在矿体附近较小范围,远离矿体位置逐步恢复至初始应力状态,三步骤开采结束后地表应力基本未发生改变,矿体开采未造成地表应力的扰动现象;结合位移变形可知,在井筒周围未发生变形,处于初始应力状态。矿山主要研究建(构)筑物均处于稳定状态。

4.3 塑性区变形分析

综合塑性区分布云图进一步对建(构)筑物稳定性进行讨论,具体如图8所示。可以看出各步骤开采结束后采场周围塑性破坏较大,破坏范围仅存在于充填体和上下盘部分围岩中。塑性区破坏形式以剪切破坏为主,较小部分区域出现拉伸破坏。与应力变形相对性,塑性区破坏范围仅局限于采场周围数米范围内,一步骤开采后塑性区破坏区域距离井筒最近距离为165 m,二步骤减小至161 m,三步骤减小至131 m。尽管塑性区逐渐扩大,整体区域并未延伸到地表及井筒周围。采场的及时充填治理避免了破坏的进一步扩大,使井筒和地表建(构)筑物依旧能够保持较好的稳定性。

图8 各步骤开采结束后模型塑性区变形

对各步骤开采过程中塑性区变形类型进行统计分析,并结合井筒距离塑性区边界最近距离进行分析,具体如图9所示。随着开采步骤的增加,剪切破坏、拉伸破坏均呈线性增大趋势,以剪切破坏为主。与之对应,井筒距离塑性区边界最近距离逐渐减小,但最终距离足够大,有足够厚度的岩层保护井筒的稳定性。

图9 塑性区破坏分析

4.4 建(构)筑物安全性分析

结合《有色金属采矿设计规范》,对研究建构筑物稳定性进行安全分析。地下矿体开采引起的岩体移动及变形一般采用的指标主要有水平变形、曲率变形和倾斜变形。

(1)倾斜变形:相邻在竖直方向的相对移动量与两相邻点间水平距离的比值,计算方法为

式中,iAB为倾斜值,mm/m;WA、WB分别为观测点A、B的下沉值,mm;lAB为观测点A、B点间的水平距离,m。

(2)曲率:两相邻的线段的倾斜差和两线段中点间的水平距离的比值,计算方法为

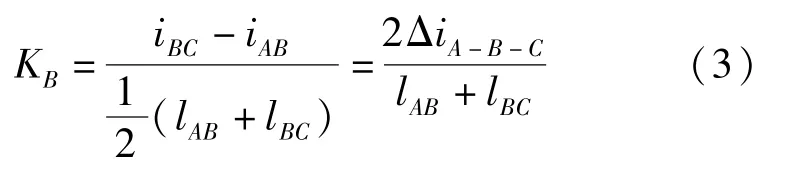
式中,KB为曲率,mm/m2;iAB、iBC分别为点A、B点间和B、C点间的倾斜值,mm/m;lAB、lBC分别为点A、B点间和B、C点间的水平距离,m。

(3)水平变形:相邻两点的水平移动差值与两点间水平距离的比值,计算方法为

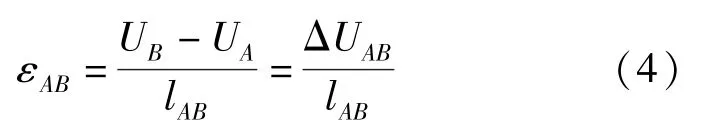
式中,εAB为曲率,mm/m2;UA、UB分别为点A、B点间的水平移动值,mm。

对研究的建(构)筑物进行保护等级划分,新南风井、地表餐厅及办公楼均属于Ⅱ级保护,Ⅱ级保护的临界变形值为:倾斜变形i=6.0 mm/m,曲率K=0.4 ×10-3/m,水平变形εAB=0.4 mm/m。

进行各步骤下建(构)筑物的水平变形、曲率变形和倾斜变形计算,结果如图10、图11所示。可以看出各步骤回采结束后,新南风井所在区域水平变形为- 0.08～0.04 mm/m,曲率为- 0.000 6～0.001 ×10-3/m,倾斜变形为-0.01～0.015 mm/m;地表餐厅及办公楼所在区域水平变形为-0.03～0.04 mm/m,曲率为-0.006～0.004 ×10-3/m,倾斜变形为-0.08～0.08 mm/m,均远小于Ⅱ级保护临界变形允许值。因此可认为矿体开采后所研究的建(构)筑物所在位置均为安全区域。

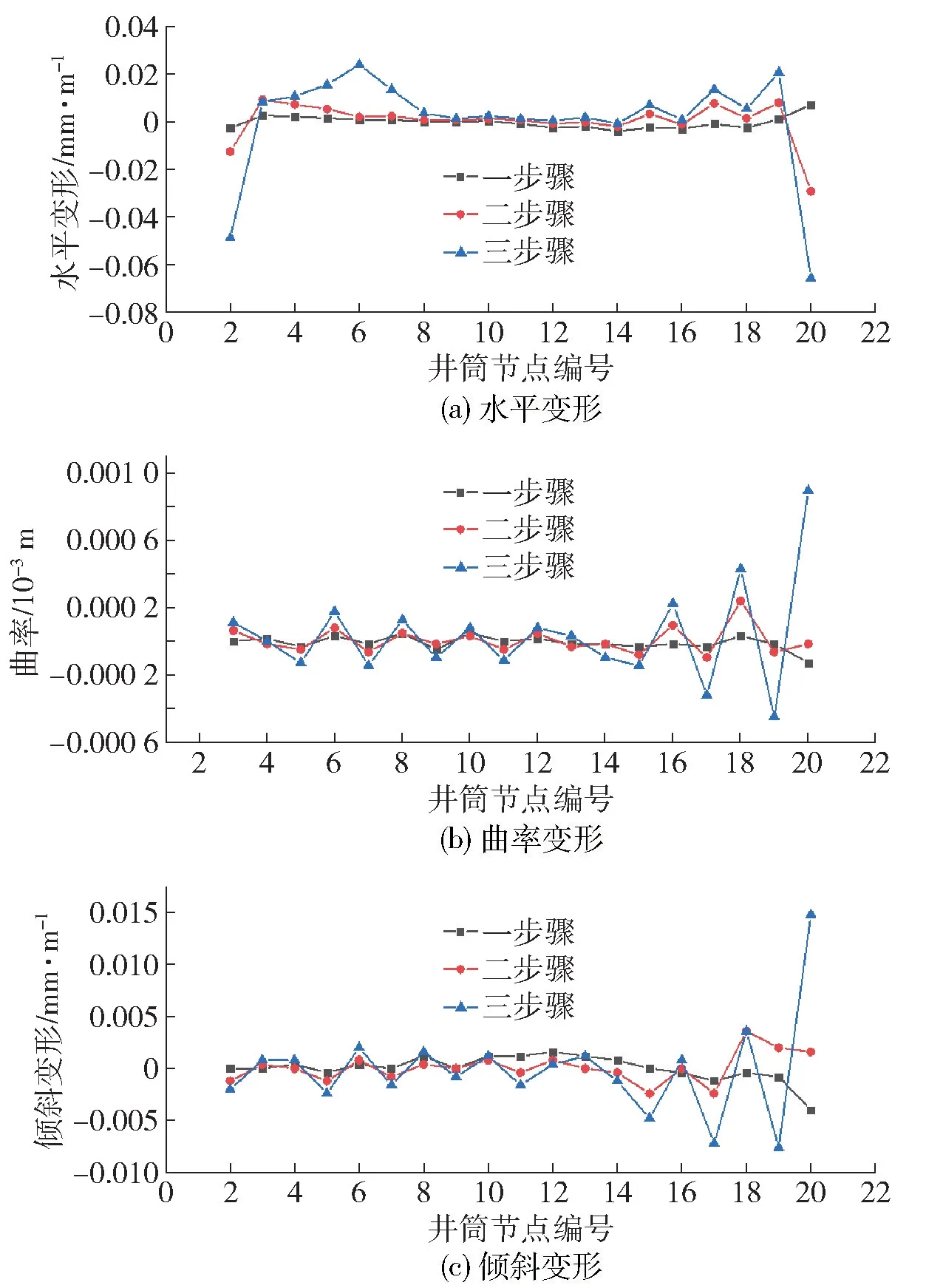
图10 开采结束后新南风井变形

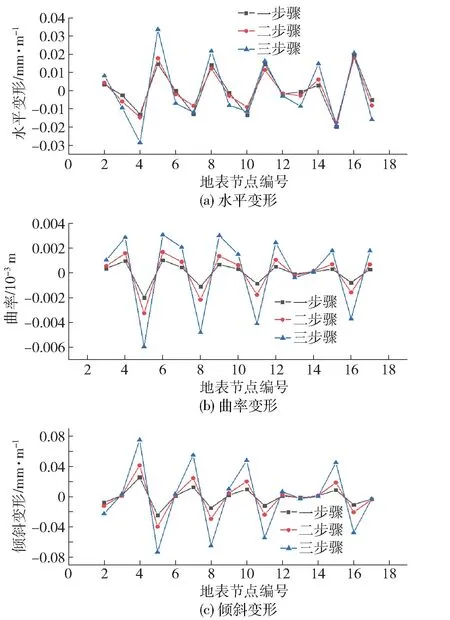
图11 开采结束后地表建筑物变形

5 结论

本文主要采用数值模拟手段,对矿区充填法开采过程中新南风井、地表餐厅及办公楼等重要建(构)筑物稳定性进行分析论证,得到结论主要有,

(1) 矿体开采后采场周围产生以剪切破坏为主塑性破坏区域,但塑性区并未延伸至地表和井筒周围。采场及时充填治理避免了破坏的进一步扩大,地表和井筒周围均能够保持较好的稳定性。

(2) 各步骤开采结束后,新南风井井筒、地表餐厅及办公楼均属于开采扰动区边界外,各建(构)筑物整体变形量较小,基本处于原岩应力状态,能够保持较好的稳定性。

(3) 选择了水平变形、曲率和倾斜变形作为建(构)筑物安全性分析指标。结果显示各指标均远小于临界变形允许值,因此可认为,地下矿体的开采不会影响各建(构)筑物的安全性。