富水砂卵石地层地铁联络横通道人工冻结数值分析

文彦鑫,伍旺,郭治岳,宋修元,尹红,蒋辉,晏启祥

（1. 西南交通大学 交通隧道工程教育部重点实验室，成都 610031；2. 中铁建大桥工程局集团第二工程有限公司，广东 深圳 518083；3. 成都轨道建设管理有限公司，成都 610041）

在建设城市地铁盾构隧道时，需要修建大量联络横通道以满足安全、逃生和通风等要求。在软弱含水地层中进行联络横通道施工时，需要对周边土体进行加固[1]。人工冻结法利用循环的低温盐水降低地层温度，将天然岩土变成冻土，提高地下工程周围土体的强度和稳定性，形成的连续冻结壁作为一种临时支撑结构和防水屏障[2]，在隧道开挖时能够抵抗周围的水土压力并隔绝隧道周围地下水的渗入，从而保证隧道顺利施工。在冻结过程中，岩土中的水会发生明显的体积变化，导致土体产生一定的冻胀变形。在重要交通路段或者高层建筑密集的地下,采用人工冻结法施工时应该对土体冻胀量进行严格控制，以免地表位移变化过大。因此，地铁联络横通道施工冻结期地层温度场和位移场的发展变化值得深入探究。

学者们对人工冻结工程的温度场和位移场进行了一系列的研究。Yan等[3-5]考虑岩土潜热释放的非线性瞬态热传导特点，研究了联络横通道人工冻结过程中冻结壁的发展过程和未冻水的转化过程，得到了冻结壁发展所需时间和未冻水体积含量的变化规律；基于考虑相变的热固耦合理论，模拟了地铁联络橫通道水平冻结和开挖施工过程，分析了地层温度场和位移场的变化规律。Cai等[6]、Song等[7]针对隧道水平冻结法施工的特点，建立了地层冻胀的弹塑性热力耦合数学模型，利用有限元软件对某浅埋大断面地铁隧道水平冻结工程的冻结温度场和冻胀位移场的分布规律进行了分析。孙立强等[8]根据室内试验结果，建立了人工冻结过程中考虑热物理参数随温度变化的热—力耦合的数值计算方法，基于某地铁联络横通道人工冻结工程,分析了土体温度场和位移场的发展规律。耿萍等[9]采用基于热弹塑性本构模型的准耦合数值分析方法，研究了在开挖过程中某隧道水平冻结工程土体应力应变的变化规律。任辉等[10]采用测点温度—时间曲线和冻土帷幕厚度两种不同分析方法对3种不同的管幕冻结方案进行了研究，根据2 m厚冻土帷幕的形成时间得到了优化设计方案。Yan等[11]采用现场检测、数值解析和数值模拟相结合的研究方法，分析了广州地铁3号线冻结法施工期间的冻结壁厚度和平均温度，验证了人工冻结法的效果。杨平等[12]以软土隧道联络横通道冻结工程为背景，对冻结壁的形成及解冻全过程进行分析，总结了冻结过程温度变化的5个阶段；Yang等[13]还提出了一种水—热—力三场耦合的分析模型，针对隧道冻结开挖工程，研究了上覆土层厚度、冻土壁厚、开挖半径和盐水温度等因素对冻胀的影响。张志强等[14]采用数值模拟研究了联络横通道人工冻结工程中的施工力学行为，对交叉部管片设计提出了要求。Kim等[15]引入分凝势（Segregation Potential）概念，建立了预测管道冻胀位移的准二维显示有限差分方程，对有无冻土两种地基条件下的管道位移进行了模拟。Kudryavtsev[16]提出了一种考虑非稳态热传导状态下水的相变过程的数值模拟方法，通过分析不同时段下土体含水量的分布可以预测冻胀变形。上述研究通过理论推导、数值模拟和现场监测等手段，对冻结法中土层温度场、土体力学性能、冻胀融沉等随时间的变化做了深入分析，其研究背景主要基于软土地层的人工冻结工程，针对砂卵石地层联络横通道冻结法施工期间土体温度场、位移场变化规律的研究尚不完善。

成都地铁10号线双流西站—空港二站区间下穿双流机场，1号联络横通道位于停机坪下，对冻结加固工程位移控制要求严格。同时，联络横通道所处地层为砂卵石地层，含水量高，渗透系数大，受冻胀融沉影响大。笔者基于该冻结加固工程，按照冻结管实际布置方式建立三维热力耦合数值模型，揭示冻结过程中温度场和位移场的变化规律，对冻结壁的不均匀分布和冻胀作用进行分析。

1 热—力耦合理论

1.1 冻结温度场数学模型

人工冻结法施工时，土体中的温度场呈非稳态变化，并且土体中的水在冻结过程中会发生相变。根据导热学理论和永久冻土理论，考虑土体冻结相变过程的非稳态导热微分方程为[17-19]

式中：T为土体温度，°C；λ为土体的导热系数，W/(m·°C)；qv为单位体积的材料在相变过程中放出或吸收的热量，W/m3；ρ为土体密度，kg/m3；c为土体比热，J/(kg·°C)；t为冻结时间，s。在非相变区，式中qv/λ=0。

非稳态导热微分方程的初始条件为

式中：T0为土体初始温度，°C。距隧道周边冻结土体无限远处的边界条件为

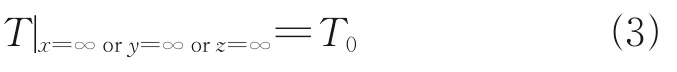
在冻结管处的边界条件为

式中：np为冻结管外表面外法线方向矢量；q为冻结管表面的热流密度，W/m2。大气与土体的对流换热边界条件为

式中：na为地表外法线方向矢量；αa为大气与土体的对流换热系数，W/(m2·°C)；Ta为大气温度，°C。根据导热微分方程及初始和边界条件可以求解土体任意时刻的温度场。

1.2 热弹塑性本构模型

在人工冻结过程中，温度场的变化会引起土体应力和位移状态的改变，并且土体弹性模量、泊松比、内摩擦角、热膨胀系数和黏聚力等力学参数会随温度发生变化，因此，对该过程进行研究需考虑温度场和应力场的耦合作用[6]。考虑土体特性进行热弹塑性分析，在弹性区域内，全应变增量可以表示为[5,9]

式中：dεe指与作用力相关的应变增量;dεT表示温度变化热膨胀产生的应变增量。其中

式中：D为弹性矩阵；α为土体热膨胀系数向量，对于各向同性材料，α=[α(T) α(T) α(T) 0 0 0]T，其中α(T)为热膨胀系数，°C-1。结合式(6)～式(8)可以得到弹性区内增量形式的本构关系为

塑性区内应力—应变增量关系为

式中：Dep为常温情况下的弹塑性矩阵；Dp为塑性矩阵。温度变化引起的应变增量d͂T和应力增量d͂T分别以初应变和初应力的形式出现在应力—应变增量关系式中。

2 冻结过程数值模拟

2.1 工程概况

成都地铁10号线双流西站—空港二站区间全长8 232.584 m，隧道顶部埋深在8.1～41.8 m之间，穿越地层主要以砂卵石、强（中）风化泥岩为主。盾构隧道内径为5.4 m，管片厚度为0.3 m。拟建联络通道区间里程为左线ZDK13+840.914、右线YDK13+830.000，联络横通道处两隧道中心距离13 m。联络横通道为直墙圆拱形结构，埋深为21.3 m，所处地层自地表以下分别为：人工填土，厚度为1.5 m；粉质黏土，厚度为8.2 m；密实卵石土，厚度为7.8 m。冻结加固区位于卵石土地层中，其含水量丰富，渗透系数大。

根据工程特点，联络通道施工拟采用“隧道内水平冻结加固土体，隧道内暗挖构筑”的全隧道内施工方案，即在隧道内采用冻结法加固地层，使联络通道外围土体冻结，形成强度高、封闭性好的冻土壁，然后在冻土壁中采用矿山法进行通道的开挖构筑施工。该联络通道共设计冻结孔61个（含4个透孔），左线冻结孔42个，右线冻结孔19个。冻结孔及测温孔尺寸及布置方式见图1。冻土壁设计厚度为2 m，设计平均温度为-10 ℃，设计冻结时间为45 d，设计需冷量为4.5×104kcal/h，冻结管采用Ф89×10 mm低碳钢无缝钢管。

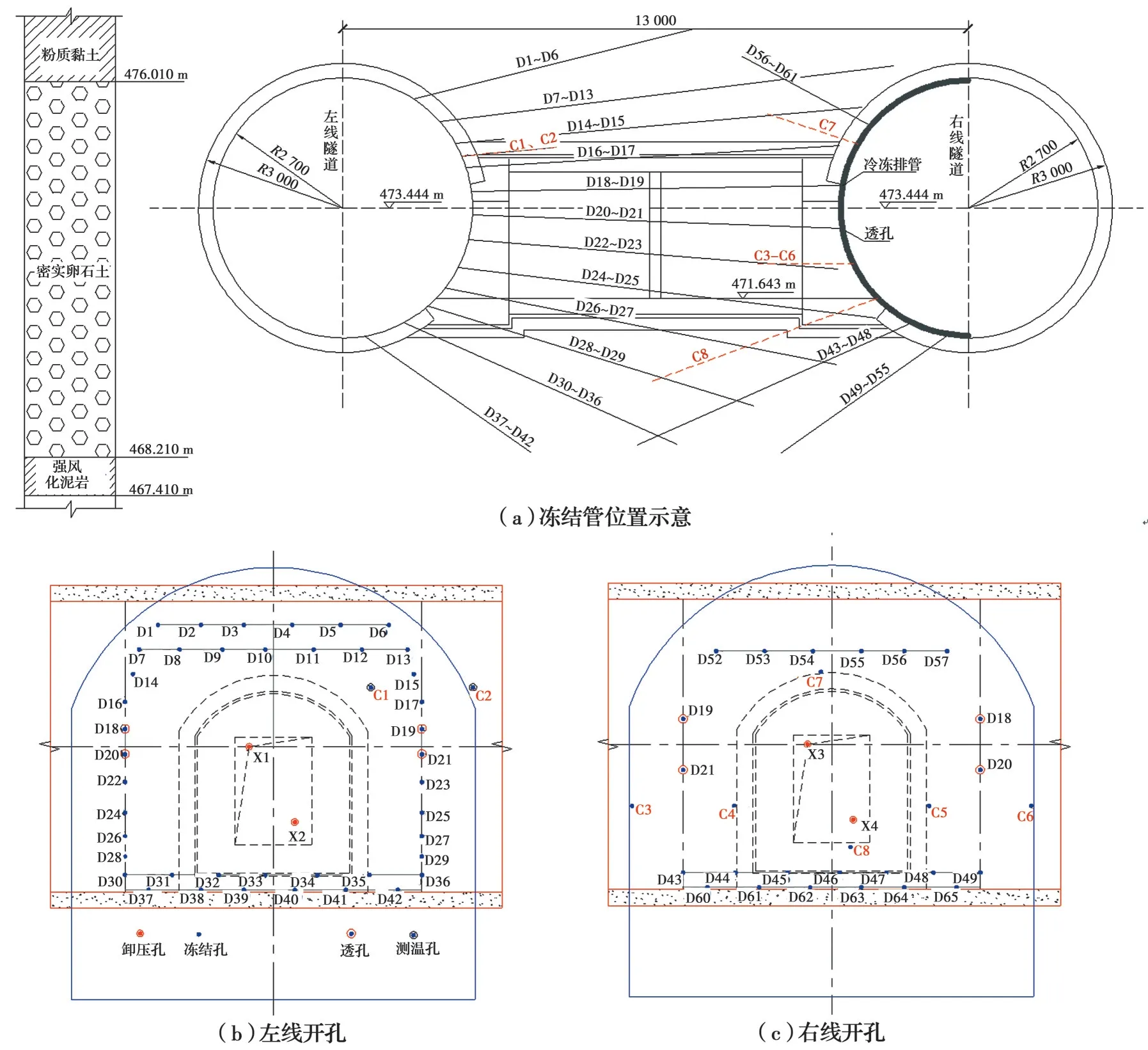
图1 联络横通道冻结管布置图Fig. 1 Layout of freezing pipes in cross passage

2.2 冻结数值模型

使用ABAQUS软件进行热—力耦合有限元数值模拟，建立模型时采用以下假定：地层为各向同性弹塑性体；冻结管周边温度均匀分布，由于冻结管长度相对较短，热传导仅主要发生在垂直于冻结管的方向，因此，不考虑沿冻结管方向的能量损失；研究范围内各土层初始温度均匀一致，不受深度变化的影响；土体模型外边界为绝热边界。模型整体尺寸为30 m×40 m×20 m。土体、隧道衬砌、冻结管均选择C3D8RT单元，即温度—位移耦合的单元。冻结管和土体之间采用tie连接。模型共划分为六面体单元88 400个，各部件网格图如图2所示。

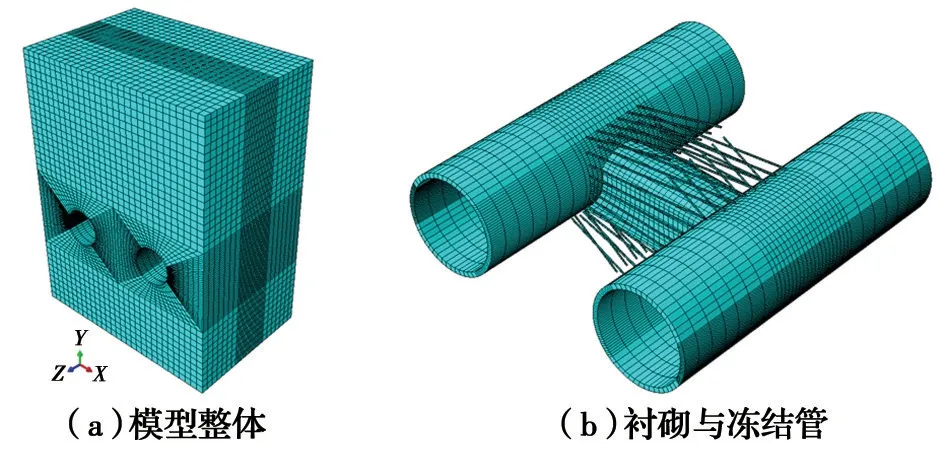
图2 有限元模型Fig. 2 Finite element model

根据相关地质资料、现场勘察和室内试验结果[20-21]，在ABAQUS软件中建立弹性模量、导热系数、热膨胀系数等随温度变化的非线性材料模型，各土层及衬砌、冻结管的物理参数见表1。根据现场土体人工冻结试验，土体相变区间为[-2 ℃,-1 ℃]，即固相温度为-2 ℃、液相温度为-1 ℃，土体的相变潜热为72.1 kJ/kg，土体的温度—热膨胀系数曲线如图3所示。荷载有重力荷载和温度荷载。由于模型中冻结管的重力对计算结果的影响较小，忽略冻结管重力，仅考虑土体和衬砌的重力；冻结管的温度根据现场监测的盐水去路温度确定，其形式是一条时间—温度幅值曲线，如图4所示。

图3 温度—热膨胀系数曲线Fig. 3 Temperature-thermal expansion coefficient curve

图4 冻结盐水温度曲线Fig. 4 Temperature curve of freezing brine

表1 不同材料物理参数Table 1 Physical parameters of different materials

位移边界条件：约束土体左右两个侧面X方向位移、土体前后面Z方向位移以及土体底部Y方向的位移。温度边界条件：冻结管和土体的初始温度与现场实测平均温度相同，取20 ℃。土体前后、左右和底部温度边界为20 ℃。土体上表面和管片内侧为对流换热边界条件，大气与隧道内空气温度取为20 ℃，土体表面及盾构隧道管片的热对流换热系数分别为8.5、2.1 W/(m2·℃)[20]。

3 地层温度场

3.1 数值模拟与实测对比

现场测温孔实测温度受施工精度和内外界环境影响较大，而数值模拟结果能从各个方面直观展示冻结过程。为验证数值模拟结果的合理性和可靠性，对现场测温孔C1、C3、C4、C8（见图1）的实测温度和数值模型对应位置处节点的模拟温度进行对比分析，温度变化曲线如图5所示。

由图5可知：1）在冻结前期（0～5 d），4个测温孔的实测温度和模拟温度均快速下降；在冻结中期（5～35 d），测温孔的模拟温度比实测温度略低，最大温差达3 ℃，因为实际冻结过程受地层不均匀性、现场施工等多种因素影响，并不是简单的温度传递过程；在冻结后期（35～45 d），测温孔的模拟温度比实测温度略高，但相比冻结中期，两者温差明显减小。2）测温孔模拟温度在25 d左右达到-2 ℃，该时间与现场实测时间的误差在4 d以内。3）数值模拟中，当温度降至约0 ℃时，测温孔温度均进入短暂的稳定阶段，这是因为液态水凝固过程中相变潜热释放，土体温度稳定在相变区间内，但现场冻结效果受周围环境因素影响较大，当温度降至0 ℃时，测温孔实测温度无明显稳定阶段。对比表明，数值模拟结果与现场监测温度吻合较好，建立的数值模型可靠。

图5 测温孔实测温度与数值模拟温度对比Fig. 5 Comparison of measured and numerical temperature of measuring holes

3.2 冻结壁动态发展

在联络横通道范围内取X=-3、0、3 m的3个监测面和联络横通道纵断面Z=0 m共4个监测面对0～45 d积极冻结期冻结壁的发展过程进行分析，监测面位置如图6所示。图7～图10为各个断面在不同时刻的温度场云图，图11为冻结壁随时间变化的形状。

图6 监测面位置示意图Fig. 6 Schematic diagram of monitoring surface position

由图7～图10可以发现：随着冻结时间的发展，冻结管周围土体温度逐渐下降，冻土范围以冻结管为中心不断向外扩展，逐渐交圈形成冻结壁，随后冻结壁厚度继续增加，在联络横通道不同位置处冻结壁厚度不尽相同。监测面1、3上冻结壁在转角位置发展良好，冻结壁四周厚度均匀，不存在死角，整个冻结壁形成一个闭合的“回”字形。监测面2上联络横通道底部和转角处冻结壁发展较慢，并且底部冻结壁交圈时间较长，约为35 d，这是因为联络横通道中心底部冻结管布置较稀疏，可通过在左右线联络通道底部冻结壁发展缓慢处增设冻结管进行改善。联络横通道顶部两侧的冻结壁发展速度比联络通道顶部中心处的冻结壁发展速度要慢，这是因为两侧土体和隧道内空气发生热对流交换，减缓了该处冻结壁的发展速度。从图11可以发现，在冻结25 d左右时，各冻结管周围的冻土柱开始交圈，形成闭合的冻结壁。

图7 监测面1冻结壁温度场（单位：℃）Fig. 7 Temperature field of freezing wall on monitoring surface 1 (Unit: ℃)

图10 联络横通道纵断面冻结壁温度场（单位：℃）Fig.10 Temperature field of freezing wall on longitudinal section of cross passage (Unit: ℃)

图11 冻结壁发展图Fig. 11 Development diagram of freezing wall

3.3 冻结壁厚度和平均温度

为了进一步分析冻结过程中冻结壁厚度和平均温度的变化情况，绘制如图12所示的不同时刻监测面1上路径1和路径2的温度分布。图中温度低于固相温度（-2 ℃）的曲线部分对应的横坐标区间长度为冻结壁的厚度。图13为监测面1～3联络横通道上部、下部及两侧冻结壁（定义为上壁、下壁和侧壁）的厚度和冻结壁内平均温度随冻结时间变化曲线。表2为冻结壁厚达到2 m所需时间，各监测面冻结壁内平均温度降至-10 ℃的时刻分别为26.5、35.1、37.8 d。

由图12、图13和表2可知：1）监测面1处冻结壁上壁厚度发展最快，30.7 d时该监测面冻结较慢的下壁厚度达到设计要求；监测面2处上壁厚度发展最快，43.2 d时该监测面发展最慢的下壁厚度达到设计要求；监测面3处冻结壁下壁厚度发展最快，约38 d时该监测面上壁和侧壁厚度达到设计要求。2）各监测面冻结壁厚的发展速度与冻结管布置方式密切相关，整体上冻结壁厚度最迟在冻结43 d后达到设计要求，冻结效果受监测面2处冻结壁下壁厚度控制，因为联络横通道中间位置底部冻结管布置最为稀疏。3）冻结壁内部土体温度比外部土体下降速度快，这是由于洞室效应，冻土向内扩展速度要大于向外扩展速度。4）从冻结壁内平均温度来看，监测面1处土体冻结壁平均温度下降最快，在26.5 d时达到-10 ℃，监测面3处冻结壁平均温度下降最慢，在37.8 d时达到-10 ℃，满足设计要求。

图8 监测面2冻结壁温度场（单位：℃）Fig. 8 Temperature field of freezing wall on monitoring surface 2 (Unit：℃)

图9 监测面3冻结壁温度场（单位：℃）Fig. 9 Temperature field of freezing wall on monitoring surface 3 (Unit：℃)

表2 冻结壁厚发展至2 m所需时间Table 2 Required time for freezing wall thickness to develop to 2 m

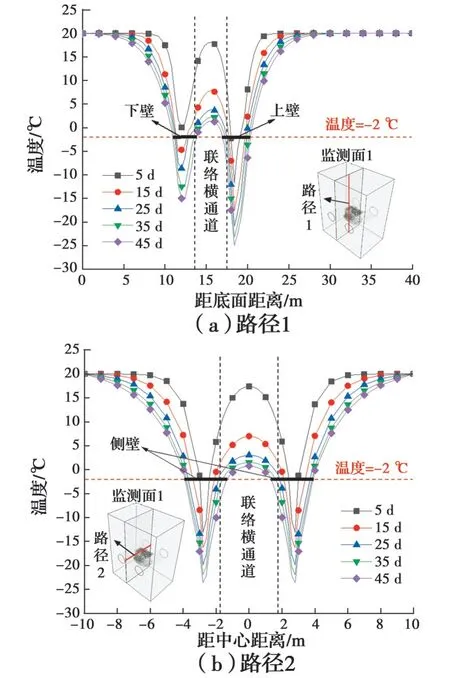
图12 监测面1上各路径随冻结天数的温度分布（单位：℃）Fig. 12 Temperature distribution of paths on monitoring surface 1 with freezing days (Unit: ℃)

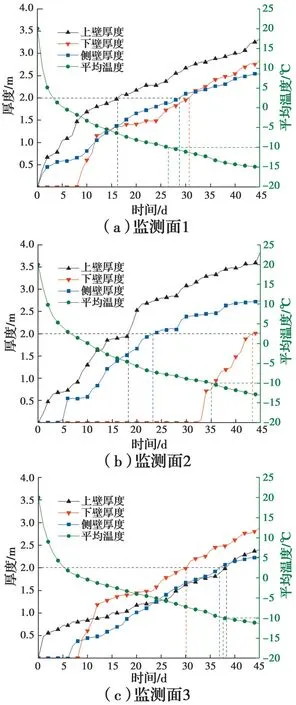
图13 冻结壁厚度与平均温度随冻结时间变化曲线（单位：m）Fig. 13 Change curves of freezing wall thickness and mean temperature with time (Unit: m)

4 位移场分析

4.1 积极冻结期位移

图14为Z=0 m剖面的竖向位移云图，从图中可见，联络横通道人工冻结区上方地表受到冻胀作用影响发生隆起。离冻结管近的土体受冻胀作用影响较大，离冻结管远的土体受冻胀作用影响较小，超过一定范围的土体不受冻胀影响。冻胀引起的最大隆起值和最大沉降值发生在联络横通道中心靠左处的竖直方向上。

图14 地层竖向位移（Z=0 m平面）（单位：m）Fig. 14 Vertical displacement of strata (Z = 0 m plane）（Unit: m)

图15为45 d积极冻结期结束时中间截面的竖向位移图和过隧道中轴线截面的沿隧道Z方向（中轴线方向）的水平位移图，提取上述两个截面在路径1、2上随冻结天数的竖向位移分布和水平位移分布，绘制如图16所示的位移分布图。从图16可以看出，联络横通道上部土体受冻胀作用影响主要产生隆起，在顶部上方2.9 m处隆起值最大，为14.8 mm；联络横通道下部土体主要产生沉降，在底部下方2.8 m处沉降值最大，为7.3 mm。距联络横通道两侧2.2 m处的水平冻胀量最大，为4.7 mm。

图15 45 d地层位移云图（单位：m）Fig. 15 Displacement cloud map of strata in 45 days(Unit: m)

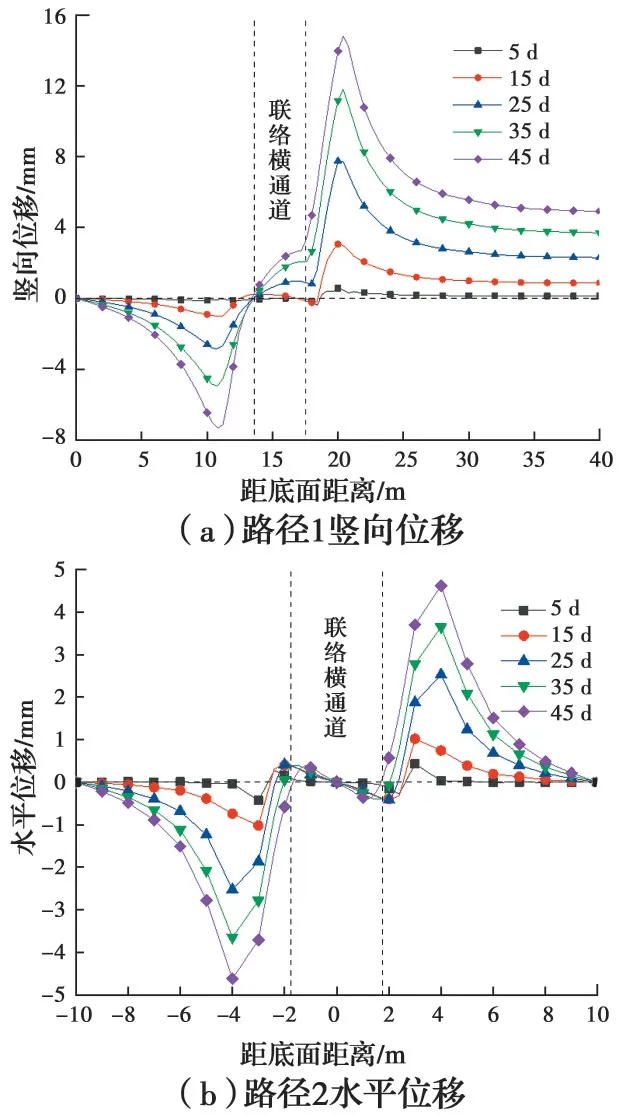
图16 各路径随冻结天数的位移分布（单位：mm）Fig. 16 Displacement distribution of paths with freezing days (Unit: mm)

4.2 拱顶沉降和净空收敛

隧道拱顶竖向位移和净空收敛分布见图17、图18。由图可知，隧道拱顶竖向位移分布曲线呈单峰分布，在联络横通道中轴线处最大，向隧道两边逐渐减小。隧道净空收敛分布曲线呈双峰分布，在联络横通道外侧1 m，即冻结管位置处最大，向隧道两边逐渐减小。

图17 隧道拱顶竖向位移分布（单位：mm）Fig. 17 Vertical displacement distribution of tunnel vaults (Unit: mm)

图18 隧道净空收敛分布（单位：mm）Fig. 18 Convergent distribution of tunnel clearance (Unit: mm)

图19为左右线拱顶竖向位移和净空收敛最大值及差值随冻结时间的变化曲线。从图19可以看出，由于左线冻结管数量较多，使得同一时刻左线拱顶竖向位移值大于右线拱顶，在冻结15 d之前，竖向位移缓慢增加，之后增长加快，可近似为线性增长，最大值为6.40 mm，在冻结壁交圈时间25 d后，左右线拱顶最大竖向位移差值稳定在0.45 mm附近；左线净空收敛较大，最大值为7.26 mm，并且在冻结25 d之前左右线净空收敛差值快速增长，之后增长减缓。

图19 左右线位移最大值及差值随冻结时间变化曲线（单位：mm）Fig. 19 Curves of maximum and difference variation of displacement between left and right tunnel with time (Unit: mm)

4.3 地表位移

45 d地表竖向位移云图如图20所示，为研究冻结过程中地表冻胀量的变化情况，在图20中联络横通道中轴线正上方地表选取X1～X9的9个数值观测点。

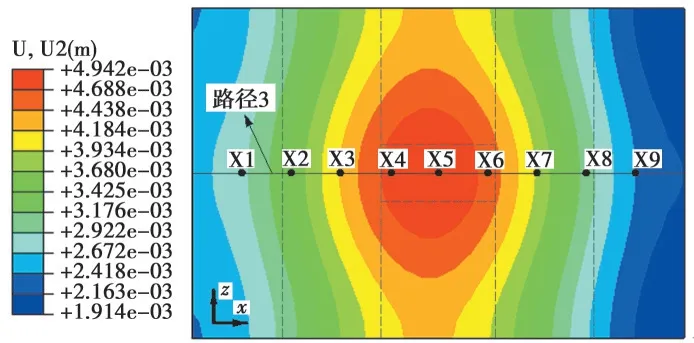
图20 45 d地表竖向位移云图（单位：m）Fig. 20 Vertical displacement cloud map on the surface in 45 days (Unit: m)

图21为观测点竖向位移随冻结时间变化曲线，图22为路径3地表中轴线上随冻结天数的竖向位移分布。由图21、图22可知：冻胀作用引起的地表隆起主要集中在联络通道冻结区正上方，最大为4.9 mm。隆起值在0～15 d内缓慢增加；15～35 d内可视为均匀增加，在X5处有最大增速0.14 mm/d；35 d时由于盐水温度降低了2 ℃，地表隆起值的增加速率变大。离冻结区越远，地表隆起值越小，可根据数值分析中地表受冻胀作用影响范围和大小采取相应措施减小冻胀破坏。

图21 观测点竖向位移随冻结时间变化曲线（单位：mm）Fig.21 Vertical displacement change curve of observation points with freezing time (Unit: mm)

图22 路径3随冻结天数的竖向位移分布（单位：mm）Fig. 22 Vertical displacement distribution of path 3 with freezing days (Unit: mm)

5 结论

以成都地铁10号线某隧道区间联络横通道人工冻结工程为依托，采用现场监测和数值模拟的方式对积极冻结期温度场和位移场的发展及分布规律进行研究，得到以下结论：

1）测温孔的现场监测温度与数值模拟结果吻合较好，同时期两者的温差在±3 ℃以内。在冻结前期（0～5 d），实测温度和模拟温度均快速下降；在冻结中期（5～35 d），实测温度的下降速度减缓并稳定在一定范围内，模拟温度在降至约0 ℃后短暂地稳定在相变区间内，但由于现场冻结效果受周围环境因素影响较大，在降至0 ℃后，实测温度无明显稳定阶段；在冻结后期（35～45 d），测温孔温度下降速度减缓。

2）冻结壁交圈约为25 d，冻结43.7 d时冻结壁厚度达到2 m，在37.8 d时冻结壁内平均温度达到-10 ℃。冻结管布置方案及相关冻结参数均满足施工要求，建议以联络横通道中间位置处下壁厚度和联络横通道右侧冻结壁的平均温度作为冻结效果的检验指标。

3）冻结壁交圈时间是冻胀变形快速增长的临界时间点，在冻结壁交圈之前，隧道拱顶竖向位移和净空收敛缓慢增加，交圈之后增长加快，可近似为线性增长。隧道拱顶竖向位移呈单峰分布，在联络横通道中轴线处最大，向两边逐渐减小。隧道净空收敛呈双峰分布，在冻结管位置处最大。冻胀作用引起的地表隆起主要集中在联络通道冻结区正上方，在15 d之前隆起值缓慢增加，15 d之后可视为均匀增加。

4）采用考虑冰水相变的非线性三维弹塑性热—力耦合数值模型分析联络横通道人工冻结工程中的冻结壁发展和冻胀作用的影响，工程概念和计算过程清晰，结果直观、可视化程度高。另外，计算中未考虑冻土的各向异性变形特征对位移场的影响及环境温度变化等因素的影响，需对这些影响进一步研究。