快递包装混合回收闭环供应链决策与协调

郑克俊，翟小可，李锦莹

（广东科学技术职业学院商学院，广东 珠海 519090）

国家邮政局公布，2021 年全国快递寄递量1 085亿件，创收1.04 万亿元，与2020 年相比，分别增长了30%和18%。为了治理快递业务迅猛增长所造成的污染，国家开展了快递包装污染专项治理。2021 年新增废旧快递包装回收网点3.6 万个，可循环快递箱使用量630 万个，电商快件不需要二次包装的占比已达80.5%。然而，快递包装废弃物造成的环境压力依然不可小觑。2020 年全国已处置包装废弃物大约1 500 万吨[1]，预计2025 年将产出4 127.05 万吨。降低快递包装污染迫在眉睫。

为了实现我国快递包装的减量化、循环再利用和绿色化的治理目标，国家发布了《关于协同推进快递业绿色包装工作的指导意见》和《关于加快推进快递包装绿色转型的意见》等政策文件，鼓励社会各界开展各种形式的快递包装绿色化转型与治理。在国家政策推动下，快递公司和互联网回收平台纷纷开展了回收再利用的有益尝试[2-3]。京东、菜鸟、苏宁分别推出“青流箱”、“回箱计划”和“共享快递盒”等循环使用快递包装的行动计划，互联网回收平台推出“爱回收”[3]“纸壳别跑”、“收纸拉”[4]等品牌的包装回收业务。国内外学者[5-11]也纷纷建言献策，提出了各种各样的促进快递包装物循环利用、减量化与绿色化的策略。

针对包装“互联网+”回收形式，国内外学者展开了深入研讨。公彦德等[12]按回收物流外包和回收物流自营2 种模式来分别探讨快递包装的回收决策问题，何波等[13]研究了以物流企业独立主导回收和以互联网电商平台独立主导回收这2 种回收模式下的快递包装回收策略。在实践中，显然存在快递公司和互联网平台同时参与回收的混合回收模式。梁喜等[14]研究了混合回收模式下的闭环供应链决策机制，虽然是以废旧家电为样本，但仍然能为快递包装的混合回收模式下的决策提供参考。许民利等[15]运用博弈论探讨了废旧产品的回收定价策略，得出“互联网+”回收将形成规模化市场的结论，这意味着快递包装的“互联网+”回收存在巨大市场空间，快递包装回收大有可为。政府的奖惩机制对快递包装回收决策的影响是研究的热点。如欧阳恋群等[16]、何海龙等[17]研究了环境税费、政府补贴、奖惩力度及消费者满意度等因素对互联网电商企业快递包装实施回收的影响。一些研究[8-11]甚至直接将政府的奖惩作为影响快递包装回收的决策变量，特别强调了政府的作用。政府、企业和消费者各自的行为决定了快递包装回收的效果和水平。在参与快递包装回收的角色定位中，企业和消费者是直接参与者，政府是间接参与者，因此，偏向认为快递包装回收供应链参与者是企业和消费者，而将政府作为一个影响供应链的外因变量来展开研究更切合实际。

文中研究快递包装生产商、快递公司、互联网回收平台和消费者构成的闭环供应链，拟运用博弈论方法，探讨在不同管控方式下供应链的利润水平，并采用收益共享-成本共担（简称收益共享）契约协调供应链参与者的利益，希望找出参与者的最优决策，为快递包装回收供应链的参与者制定回收策略提供决策支持，为政府提供政策建议。

1 建模

1.1 模型概述

“互联网+”回收具有信息处理能力强、价格透明、服务便捷、市场潜力巨大等优势，因此文中引入互联网回收平台开展回收业务。快递包装生产商、快递公司、互联网回收平台和消费者共同组成闭环供应链，政府作为外因变量，通过税收-补贴这一最佳调控机制[5]对供应链产生影响。在正向物流中，包装生产商将生产的快递包装物批发给快递公司，伴随电商业务，快递公司将包装物销售给消费者。在逆向物流中，快递公司通过快递网点回收消费者返还的废旧包装物，互联网回收平台接收消费者网上订单来回收废旧包装物。快递公司与互联网回收平台各自将回收的废旧包装物销售给包装生产企业，包装生产企业利用回收的废旧包装物再生产出新的快递包装物（图1）。

图1 快递包装混合回收闭环供应链Fig.1 Closed loop supply chain of mixed recycling for express packages

1.2 模型假设

1）假设所有可重复使用的快递包装容器都是纸箱。由于纸箱生产商通过回收再制造生产出的纸箱与采用原材料生产出的纸箱功能一样、质量基本无差异，因此假设生产出的纸箱销售价格是一样的。又由于纸箱单位处置成本较低，且回收的大部分纸箱都流向纸箱生产企业，因此不考虑纸箱的废弃处置成本。

2）假设快递公司回收与互联网平台回收不存在竞争关系，闭环供应链中各参与者处于均等地位，信息对称，风险中性。

3）参考文献[13]，假设纸箱的市场需求量为Q件，其中Q=Q0-ωP（Q0为纸箱市场最大需求量，ω为纸箱回收价格敏感系数[13,18]，ω∈[1,1 000]，P为纸箱回收价格（元/件）。纸箱的需求量等于市场最大需求量减去回收再利用量。回收再利用量受回收价格和价格敏感系数影响。

4）参考文献[12]，假设纸箱回收量X（单位：件)与回收价格P呈线性关系，Xi=λ MPi。其中，λ表示消费者对回收价格的敏感程度[12,19]，λ∈[0,1]，M表示纸箱回收市场规模，单位为件。下标i∈{1,2,3}，1—3分别代表纸箱生产商、快递公司和互联网回收平台。

5）其他符号描述。纸箱批发价为P11（元/件），纸箱生产商给互联网回收平台的回收转移价格为P12（元/件），纸箱边际生产和边际再生产成本分别为c1（元/件）和v1（元/件），互联网回收平台的回收价格和单位运营成本分别是P3（元/件）和c3（元/件），政府给纸箱生产商的单位补贴和向其征收的单位环境税额分别是a（元/件）和b1（元/件），纸箱回收率为φ（%），纸箱生产商、快递公司和互联网回收平台的利润分别是 1∏、2∏和 3∏（元）。

2 分散决策

2.1 利润函数

根据图1 模型及上述假设，计算出纸箱生产商、快递公司、互联网回收平台的利润函数分别为：

式中：第1 项为采用原材料制造新纸箱获得的利润；第2 项表示回收再制造纸箱所获利润；第3 项表示政府对未回收纸箱征收的环境税费。

式中：第1 项为快递公司将纸箱批发给互联网回收平台所获的利润；第2 项表示快递公司回收废旧纸箱所获利润。

式中：P12X3为互联网回收平台将可再制造的废旧纸箱卖给制造商获得的收益；（P3+c3）X3为互联网平台回收费用及运营成本。

2.2 Stackelberg 博弈

博弈论（Game Theory）是研究在特定条件下，决策者依据拥有的信息，各自从备选方案中选择最优方案、采取行动，从而获得收益的理论。博弈的最终目标是实现各参与方利益最大化的均衡。

Stackelberg 博弈是一个动态博弈，在博弈中，各参与方依据先后顺序做决策。其中领导者为先做出决策的优势方，跟随者为劣势方。领导者的决策除了考虑自身收益外，还会预判跟随者的反应；而跟随者在领导者决策基础上，选择对自己最有利的方案。决策者之间是相互制约、相互影响的关系。

文中所研究的是完全信息下的动态博弈，制造商为领导者，快递公司和互联网回收平台为跟随者，他们之间构成Stackelberg 博弈。

2.3 博弈均衡时的最优解

结论1：分散决策时，供应链参与者博弈均衡时的最优解为：

上标*表示最优值。

证明：供应链的参与者形成Stackelberg 博弈，用逆向求解法求解。

将X3=λMP3代入（3）式，并分别求 3∏关于P3的一阶、二阶偏导数，得：

利用海赛矩阵（Hessian Matrix）来判定多元函数的极值是求解最优化问题的常用方法。判定依据是：如果海赛矩阵正定，则存在局部极小值；如果负定，则存在局部极大值。海赛矩阵是正定、负定或不定，一般采用矩阵的顺序主子式来判定。如果矩阵的各阶顺序主子式都为正，则为正定；如果奇数阶顺序主子式为负，偶数阶顺序主子式为正，则为负定；如果上述两个条件都不满足，则为不定。

将式（12）—（13）代入式（9）—（11），化简整理可得式（4）—（8），即结论1 的均衡解。证毕。

2.4 最优利润

根据最优解，计算出纸箱生产商、快递公司和互联网回收平台的最优利润分别见式（14）—（16）。

回收率为式（18）：

3 集中决策

3.1 集中决策均衡解

集中决策时供应链系统的利润为制造商、快递公司和互联网回收平台的利润之和，表示为：所示。证毕。

3.2 集中决策时供应链的最优利润

将式（20）—（22）代入（19）式，计算出最优利润，列式（23）。

3.3 集中决策与分散决策对比

结论3：集中决策时的销售价低于分散决策时的销售价。

证明：根据式（6）和（20）作差计算得：

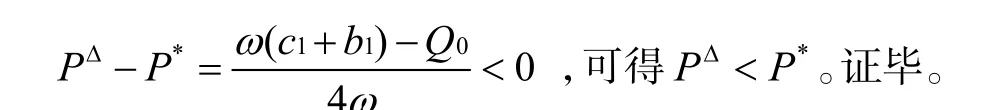
结论4：集中决策时的回收价高于分散决策时的回收价。

证明：根据式（7）和（21）作差计算得：

结论5：集中决策的效果好于分散决策。

证明：这里以供应链系统的利润作为评价的依据，利润高的比利润低的效果好。

结论5 说明，集中决策削减了供应链的“双重边际化”，实现了供应链参与者共赢的目标。

4 契约协调

4.1 契约协调后的利润函数

根据《关于推进电子商务与快递物流协同发展的意见》中提出的“建立和完善快递包装生产者责任延伸制”文件精神，快递包装生产商应承担部分废旧包装回收的成本，并从快递包装件销售收入中取得相应的补偿，因此，这里采用收益共享契约协调机制来协调供应链系统中参与者的利益。假设快递包装生产商按比例k1承担快递公司的回收成本并享受相应的销售收益，按比例k2承担互联网回收平台的回收成本，k1、k2∈（0,1）。

契约协调后，快递包装生产商、快递公司和互联网回收平台的利润函数分别为

4.2 契约协调后的最优解

以下用上标Ω 表示使用契约协调后闭环供应链的最优解。

结论6：使用契约协调后供应链系统的最优解为

联立（33）—（35）求解即可得出式（31）—（32）所示条件。证毕。

4.3 契约协调后的最优利润

分别将式（28）—（32）代入式（25）—（27）计算，可得使用收益共享契约协调后参与者最优利润，列式（36）—（38）所示。

契约协调后供应链系统的总利润列式（39）。

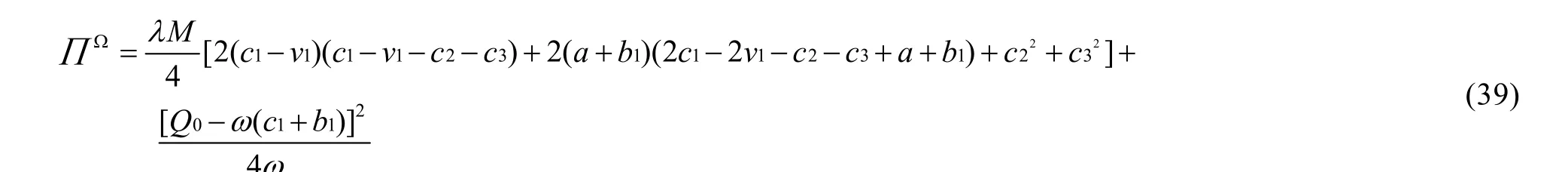
5 实证

为了验证结论，进行数值验算。结合快递包装回收的实际状况[2-3]，参考文献[13],设定参数如下：市场最大可能需求量Q0=3 000 件，价格敏感系数ω=600[18]，消费者对回收价格的敏感程度λ=0.4[19]，回收市场规模M=1 000 件，纸箱的边际生产成本c1=3.5元/件，边际再生产成本v1=1.2 元/件，互联网回收平台的纸箱单位运营成本c3=0.35 元/件，快递公司的纸箱单位运营成本c2=0.25 元/件，政府环境税单位税额b1=0.8元/件，政府的单位补贴a=0.4 元/件。契约比例为k1、k2（k1、k2在0 到1 之间取值，或用0%～100%），见表1。从表1 算例计算结果得出结论如下。

1）与分散决策比较，集中决策下销售价格4.65元/件低于分散决策时的4.83 元/件，快递公司回收价格1.63 元/件和互联网平台回收价格1.58 元/件均高于分散决策时的0.83 元/件和0.78 元/件，供应链系统利润2 122.00 元也明显大于分散决策时的1 591.63 元。结论3—5 得到验证。

2）从表1 第2、4 行看出，当使用收益共享契约协调后，纸箱生产商的批发价、销售价格都分别比分散决策时的4.65 元/件和4.83 元/件低；从表1 第5、6 行看出，快递公司和互联网回收平台的纸箱回收价格均分别比分散决策时的0.83 元/件和0.78 元/件高。

3）在使用契约协调时，不同的共享比例对闭环供应链参与者生产经营活动产生影响。博弈的结果是造成回收转移价格出现波动（从表1 第3 行数据可以得到验证），从而对供应链参与者利润造成影响（表1 第7—9 行数据）。总体而言，除了少数情况（表1中画波浪线的3 个数据）出现低于分散决策情况外，大多数情况下供应链参与者的利润均显著高于分散决策时的利润，利润提高的幅度取决于协调比例的大小。因而，为了达到利润最大化目标，供应链参与者可能会针对协调比例（k1和k2的不同取值）展开博弈，谈判实力强的企业会选择对自身更有利的协调比例，在协调机制中获得更大的系统利润。

表1 算例计算结果Tab.1 Calculated results by the example

4）采用契约协调后，供应链系统利润2 122.00元也达到了集中决策时最优值，并显著大于分散决策时的1 591.63 元。这正好验证了契约协调机制不仅能使系统利润达到最大化，还能使供应链达到完美协调。

6 结语

伴随我国快递业务量不断快速增长，采用一定的契约来协调快递包装回收参与者的利益，提高废旧快递包装回收率，对发展低碳绿色经济、实现碳达峰碳中和具有重要意义。在快递包装的“互联网+”混合回收闭环供应链系统中，集中决策的效果显著优于分散决策；收益共享契约不仅能协调参与者的个体利益，还能提高供应链的整体利润，激发参与者的回收积极性，因此，为了提高快递包装的循环利用水平，治理快递包装污染，政府应从集中决策角度统筹规划，加强对供应链的统一领导，让参与回收快递包装物的企业和消费者达成共识，统一行动。建议政府大力推广“互联网+”混合回收方式，通过实施税收-补贴监督激励机制和收益共享契约协调机制，来提高我国快递包装回收参与者的积极性，激励他们尽最大努力来提高快递包装回收量，解决快递包装物回收率低的问题，实现企业、消费者和社会共赢。

文中研究仅考虑一个快递包装生产商、一个快递公司和一个互联网回收平台组成的供应链，而未考虑多个参与者并存、多个参与者相互竞争等情形，另外供应链各参与者也可能存在信息不对称的问题。这些扰动因素均可能会对供应链的决策产生影响，这些都是未来进一步研究的方向。