Na0.5Bi0.5TiO3-BaTiO3-SrTiO3陶瓷的相图及电致伸缩性能

谷吉海，曹文萍，王剑菲，巩雪

（哈尔滨商业大学 轻工学院，哈尔滨 150028）

压电陶瓷的电致伸缩效应因具有体积小、位移分辨率高、温度稳定性好、响应速度快、滞后性小、不需要极化预处理等优点而备受关注，在国防、生物医学、光电子、喷墨印刷等领域具有重要应用[1-2]。例如，在压电喷墨技术中，利用压电陶瓷的电致伸缩效应能够精准控制墨滴的大小、浓度和喷射速度，墨滴在喷射过程中不会出现散点和扩散等现象。目前，由于铅基压电陶瓷具有较大的电致应变（0.1%）和较高的电致伸缩性能（10-2m4/C2），因此成为市场中应用较多的电致伸缩材料体系[3]。由于铅基陶瓷材料在生产和使用过程中会对环境和人类健康造成较大的危害，因此研究高性能无铅电致伸缩材料体系具有重要的意义。

通常，铁电材料处于居里温度（tc）之上，或弛豫铁电体在相变温度降至室温附近时能够得到较大的电致伸缩性能。作为典型的无铅弛豫铁电材料，Na0.5Bi0.5TiO3（NBT）陶瓷材料具有铁电性较强、居里温度较高和相变较复杂等特点，成为最有希望代替铅基材料、应用前景较好的无铅电致伸缩材料。目前的研究主要通过化学掺杂手段调控NBT 基陶瓷材料的相变温度，从而在室温附近获得较大的电致伸缩性能[1,4-10]。在这些研究体系中，(1-x)BNT-xBT（BaTiO3）无铅陶瓷体系在准同型相区（x为0.06～0.07）时，由于其介电常数具有优异的强频率弥散特性、压电性能和电致应变等，因而引起了广泛的关注[1,11]。此外，大量研究发现，在室温下为顺电相的SrTiO3（ST）能够破坏NBT 陶瓷的铁电性，降低其相变温度，从而调控NBT 陶瓷的相结构[12]。前期，笔者进行了ST调控准同型相区0.94BNT-0.06BT 陶瓷的研究工作，研究发现(1-x)[0.94NBT-0.06BT]-xST 陶瓷的相结构随着ST 掺杂含量的增加会出现明显的变化[13-14]。其中，在x=0.04 时陶瓷的相结构为四方相（T）和三方相（R）共存，该组分表现出优异的压电性能（d33=205 pC/N）；在x=0.10 时，陶瓷的相结构为铁电相（FE）和弛豫相（RE）共存，该组分表现出优异的应变性能（S=0.34%）；在x=0.30 时，陶瓷的相结构为弛豫相，该组分表现出优异的储能性能（W=0.98 J/cm3，ƞ=82%）。

在驱动器、微位移器等精密设备的应用中，材料的应变和滞后是衡量其性能优劣的2 个重要参数。文中在给出(1-x)[0.94NBT-0.06BT]-xST 陶瓷相图的基础上，阐明该体系不同相区应变的来源，得到应变滞后的大小。其中，在弛豫相区，NBT 基陶瓷的退极化温度降至室温以下，陶瓷内部形成了纳米极性微区，有利于得到应变滞后小且性能优异的电致伸缩效应。文中重点研究弛豫相区ST 掺杂量对陶瓷铁电、应变和电致伸缩性能的影响规律，以期为大电致伸缩材料的研制提供一定的指导。

1 实验

1.1 材料及仪器

主要材料：碳酸钠（Na2CO3）、碳酸钡（BaCO3）、三氧化二铋（Bi2O3）、碳酸锶（SrCO3）、二氧化钛（TiO2），均为分析纯，国药集团。

主要仪器：电热恒温鼓风干燥箱，DHG-9075A，上海吉众仪器有限公司；粉末压片机，HY-12，天津天光光学有限公司；高温烧结炉，KSL-1700X-A1，合肥科晶材料技术有限公司；全方位行星球磨机，PMQW4L，南京驰顺科技发展有限公司；铁电综合测试系统，Technologies Precision Premier Ⅱ，美国Radiant 公司；应变测试仪，AE SP-S120E，美国Radiant 公司；数字示波器，Tektronix 460A，美国Radiant 公司。

1.2 粉体制备

按照化学计量比（(1-x)[0.94NBT-0.06BT]-xST，x表示物质的量分数，x为0.25～0.40）称量所需药品，并放入尼龙球磨罐中，采用无水乙醇作为球磨介质，球料比为5 ∶1，在转速为300 r/s 条件下球磨12 h。将球磨后的粉体放在温度为80 ℃的烘箱内烘干，随后将粉体在850 ℃的条件下预烧2 h。将预烧后的粉体按第1 次球磨的工艺进行二次球磨，最后将球磨后的粉体在 80 ℃的烘箱内烘干， 得到(1-x)[0.94NBT-0.06BT]-xST 陶瓷的粉体。

1.3 块体制备

利用粉末压片机将(1-x)[0.94NBT-0.06BT]-xST陶瓷的粉体压成直径约为1 cm、厚度约为1 mm 的圆片。在压片时，将质量分数为5%的聚乙烯醇（PVA）加入粉体内进行造粒。随后，将圆片放入烧结炉中，以2 ℃/min 的速度升温至600 ℃，保温1 h，以排出压片时加入的PVA。最后将陶瓷片放入烧结炉中，以10 ℃/min 的速度升至1 150 ℃，保温2 h，得到致密的陶瓷。为了测试电性能，需将陶瓷进行抛光，并在陶瓷片的上下表面刷涂银浆，在500 ℃下保温0.5 h。

1.4 测试与表征

采用美国Radiant Technologies Precision PremierⅡ铁电综合测试系统、AE SP-S120E 应变测试仪、Tektronix 460A 数字示波器测试(1-x)[0.94NBT-0.06BT]-xST 陶瓷的电滞回线和蝶形曲线。其中，电场强度为30～60 kV/cm，周期为500 ms。

2 结果与分析

2.1 陶瓷相图和应变来源

相结构是决定陶瓷性能优劣的重要因素，(1-x)[0.94NBT-0.06BT]-xST 陶瓷相结构随ST 含量的变化情况见图1。其中，退极化温度（td）和居里温度（tm）分别为频率10 kHz 时介电损耗和介电常数峰值对应的温度[13-14]。由于 ST 的居里温度（-168 ℃）远低于0.94NBT-0.06BT 陶瓷的居里温度，因此td和tm随着ST 含量的增加均出现不同程度的降低。0.94NBT-0.06BT 陶瓷在室温时的相结构为R、T 两相共存（准同型相区，MPB），随着ST 含量的增加，在室温时的相结构由两相共存变为四方铁电相。前期研究发现在x=0.08 时，样品的电滞回线变瘦，且压电性能明显降低，故其 MPB 相区x为0.00～0.06。MPB 相界附近自发极化的可能取向增多，电畴更易翻转，陶瓷材料表现出优异的压电性能[15]。此时，应变曲线为典型铁电体的蝴蝶型曲线，有明显的负应变，见图1b。一般来说，铁电材料中的应变主要来源于逆压电效应、电致伸缩效应、非180o畴转向和电场引发的相变等。 MPB 相区内(1-x)[0.94NBT-0.06BT]-xST 陶瓷的应变主要来源于逆压电效应引起的晶格变形和电场作用下的非180o畴转向。

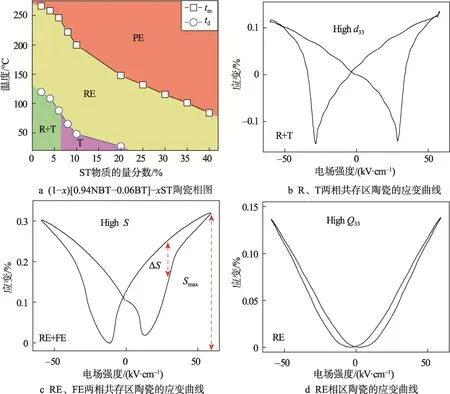
图1 (1-x)[0.94NBT-0.06BT]-xST 三元系陶瓷的相图及应变曲线Fig.1 Phase diagram and S-E curves of (1-x)[0.94NBT-0.06BT]-xST ternary ceramics

在x为0.08～0.20 组分范围内时，随着ST 含量的增加铁电相/弛豫相的相变温度逐渐降低，表明弛豫相所占比例增多，铁电相所占比例逐渐减少。当ST的物质的量分数增加到0.20 时，退极化温度降至室温附近（td=28 ℃），此时(1-x)[0.94NBT-0.06BT]-xST陶瓷室温相结构以弛豫相为主。在x为0.08～0.20 组分范围内，铁电相与弛豫相共存时，由于铁电相与弛豫相具有相近的自由能，在外加电场作用下弛豫相极易转变为铁电相，从而得到较大的应变，如图1c 所示。此时，与畴反转相关的负应变较小，由电场引发相变导致的正应变明显增大，但应变滞后性（H=ΔS/Smax）往往较大。

在x为0.25～0.40 组分范围内时，退极化温度降至室温以下，即在室温时，(1-x)[0.94NBT-0.06BT]-xST 陶瓷的相结构为弛豫相。在弛豫相区，样品表现出“束腰型”电滞回线和负应变为零的应变曲线，如图1d 所示。此时，应变主要来源于样品晶格本征变形产生的电致伸缩。由此可见，在该组分区有利于获得较大的储能性能和电致伸缩系数。下面将系统地分析弛豫相区(1-x)[0.94NBT-0.06BT]-xST 陶瓷的电致伸缩性能。

2.2 介电弛豫行为分析

纳米极性微区的形成及弛豫性的增强有利于获得较大的电致伸缩性能[16]。对于弛豫型铁电体，可以采用其弥散度γ来描述弛豫程度。其中，在γ=1 时为标准铁电体；在γ=2 时为理想的弛豫型铁电体；当铁电体中存在弛豫型相变时，1＜γ＜2。弥散度γ通常用修正的居里-外斯定律进行表征，见式（1）[2]。

式中：ε为温度t时所对应的介电常数；εm为最大的介电常数；tm为εm对应的温度；C为居里常数。

在10 kHz 时，(1-x)[0.94NBT-0.06BT]-xST 三元系陶瓷ln（t-tm）与ln（1/ε-1/εm）的关系及线性拟合结果见图2。从图2 可以看出，所有样品的ln（t-tm）与ln（1/ε-1/εm）均表现出良好的线性关系，且均可分别用一条直线进行拟合。根据拟合结果可知，弥散度γ随着ST 含量的增加逐渐增大。当x=0.40 时，陶瓷的弥散度系数相对最大，γ=1.89，表明其相变的弥散程度接近于完全弥散。(1-x)[0.94NBT-0.06BT]-xST 陶瓷的弛豫性主要由其A 位晶格（Na+、Bi3+、Ba2+、Sr2+等4 种离子）占据造成的，随着ST 含量的增多，A 位离子的无序度增加，使得陶瓷的弛豫性逐渐增强，有利于获得较大的电致伸缩性能。

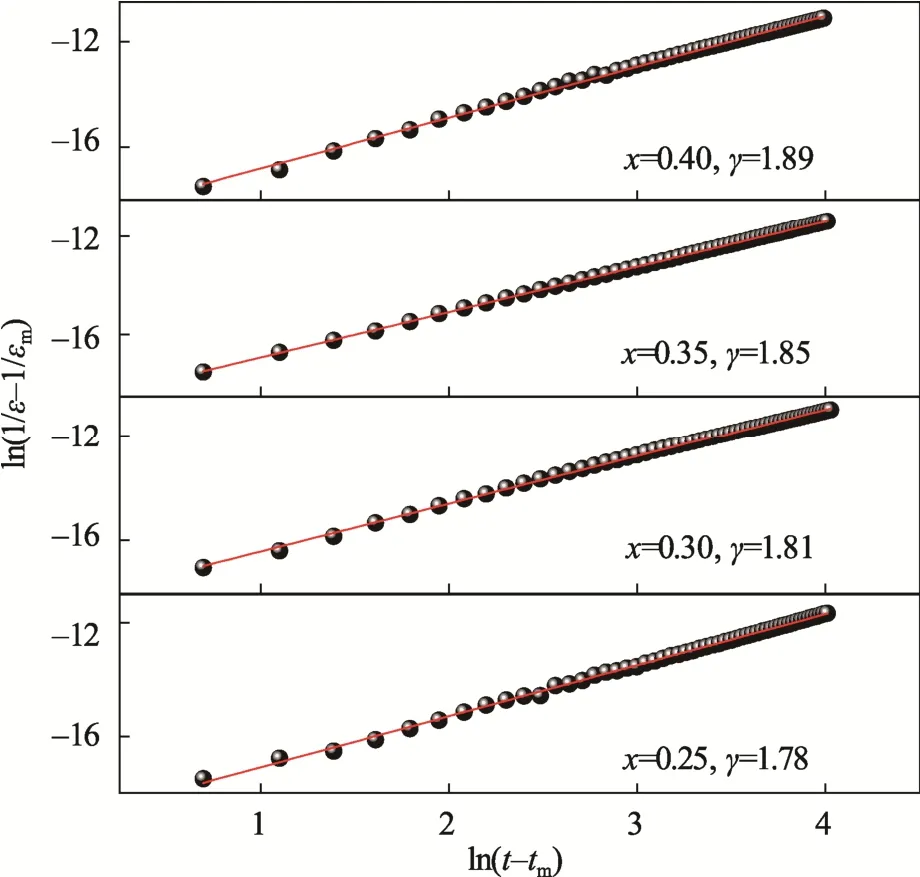
图2 (1-x)[0.94NBT-0.06BT]-xST 陶瓷ln（t-tm）与ln（1/ε-1/εm）的线性拟合Fig.2 Linear fitted ln(1/ε-1/εm) as function of ln(t-tm) for(1-x)[0.94NBT-0.06BT]-xST ceramics

2.3 铁电性能

陶瓷的电致伸缩性能与其极化强度和电致应变有关。(1-x)[0.94NBT-0.06BT]-xST 陶瓷在电场强度30～60 kV/cm 范围内的电滞回线见图3。由图3 可见，所有样品在室温下都表现出剩余极化强度Pr较小的“束腰型”电滞回线，这表明当ST 的物质的量分数高于25%时，(1-x)[0.94NBT-0.06BT]-xST 陶瓷的铁电有序被扰乱，在电场强度为0 kV/cm 时样品的相结构为弛豫相状态。当施加电场时，样品的最大极化强度Pmax随着电场强度的增加出现不同程度的增大，但陶瓷的矫顽场Ec和剩余极化强度Pr基本不变。

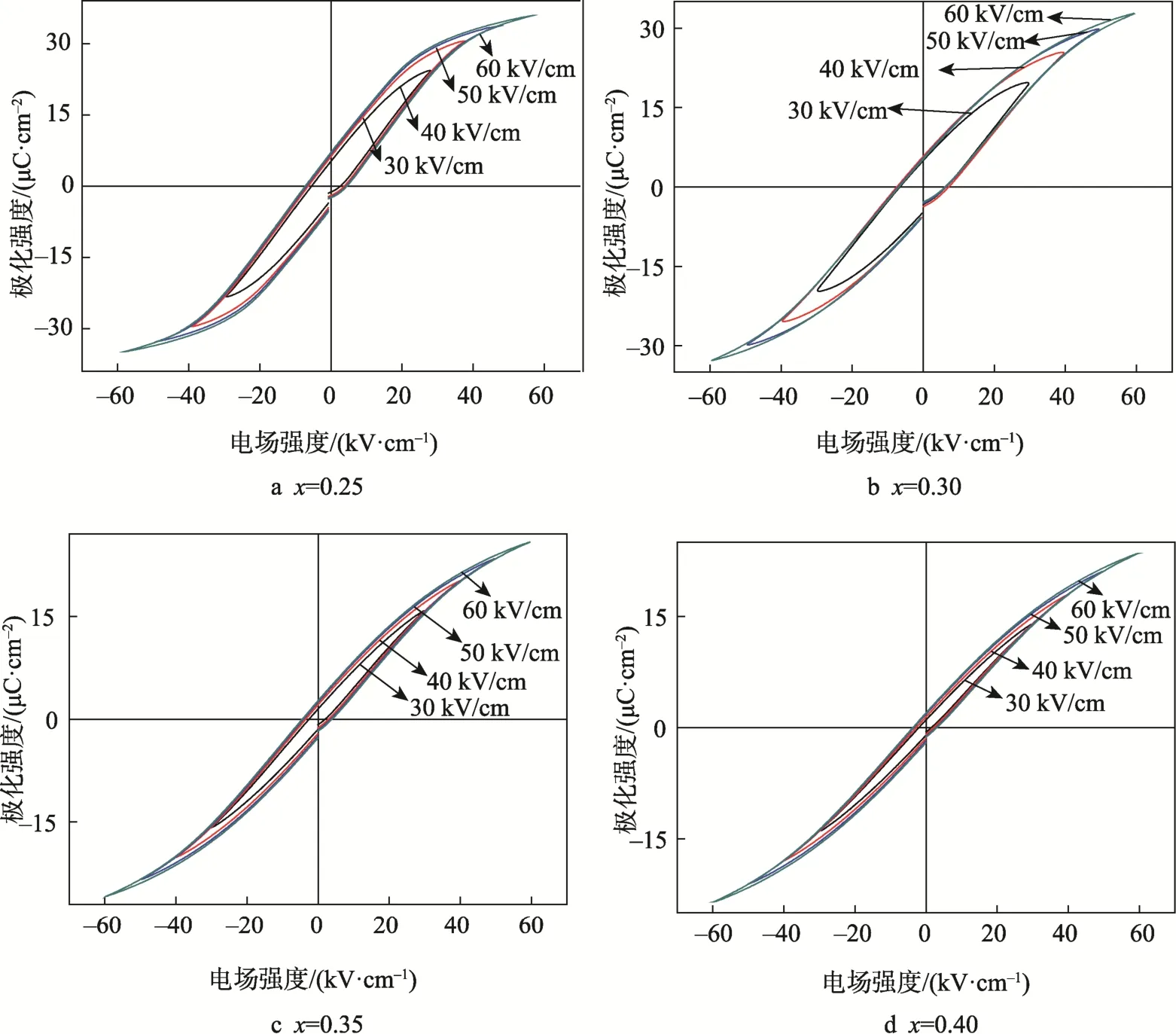
图3 (1-x)[0.94NBT-0.06BT]-xST 陶瓷室温电滞回线Fig.3 P-E loops of (1-x)[0.94NBT-0.06BT]-xST ceramics measured at room temperature

为了分析ST 含量对陶瓷铁电性能的影响，研究了在电场强度60 kV/cm 下(1-x)[0.94NBT-0.06BT]-xST 陶瓷剩余极化强度Pr、最大极化强度Pmax及矫顽场Ec随ST 含量的变化情况，见图4。由图4 可见，随着ST 含量的增加，Pmax、Pr和Ec均出现不同程度的降低，其中Pr由6.16 μC/cm2降至2 μC/cm2，Ec由6.14 kV/cm 降至2.66 kV/cm，Pmax由36.7 μC/cm2降至23.5 μC/cm2。出现该现象的原因主要有以下2 个方面：ST 在室温时为顺电相，其极化强度和矫顽场均较小，因此(1-x)[0.94NBT-0.06BT]-xST 陶瓷的极化强度和矫顽场随着ST 含量的增大而减小；由相图可知，(1-x)[0.94NBT-0.06BT]-xST 陶瓷在x为0.25～0.40 内时的室温相结构为弛豫相，即在无序的基体中分布着许多能够产生局域电场或自发极化的化学有序区域，从而能够产生纳米尺寸的极性微区[17]。这些具有纳米尺寸的极性微区具有抑制铁电有序的作用，导致材料Pmax的降低。当施加较强的电场时，能够在弛豫铁电体中诱发长程偶极子，撤去电场后，弛豫铁电体又回到短程有序的状态，从而表现出较小的Pr。

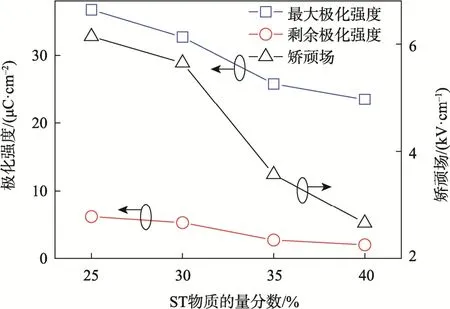
图4 (1-x)[0.94NBT-0.06BT]-xST 陶瓷Pr、Pmax 和Ec 随成分的变化情况Fig.4 Variation of Pr, Pmax and Ec of(1-x)[0.94NBT-0.06BT]-xST ceramics

2.4 电致应变性能

在应变性能中，电致伸缩材料需满足在相对不大的电场强度下具有较大的应变，且应变与电场强度的关系没有滞后或滞后较小。(1-x)[0.94NBT-0.06BT]-xST 陶瓷在外加电场强度 30～60 kV/cm 下的应变（S-E）曲线见图5。由图5 可见，所有样品均表现出抛物线型应变曲线，在电场作用下的应变均为正值，且随着电场强度的增大，应变都随之增大。此外，x为0.25～0.35 时的应变曲线都具有一定的滞后性，对于x=0.40，应变曲线表现出基本无滞后的二次方的电致伸缩效应。

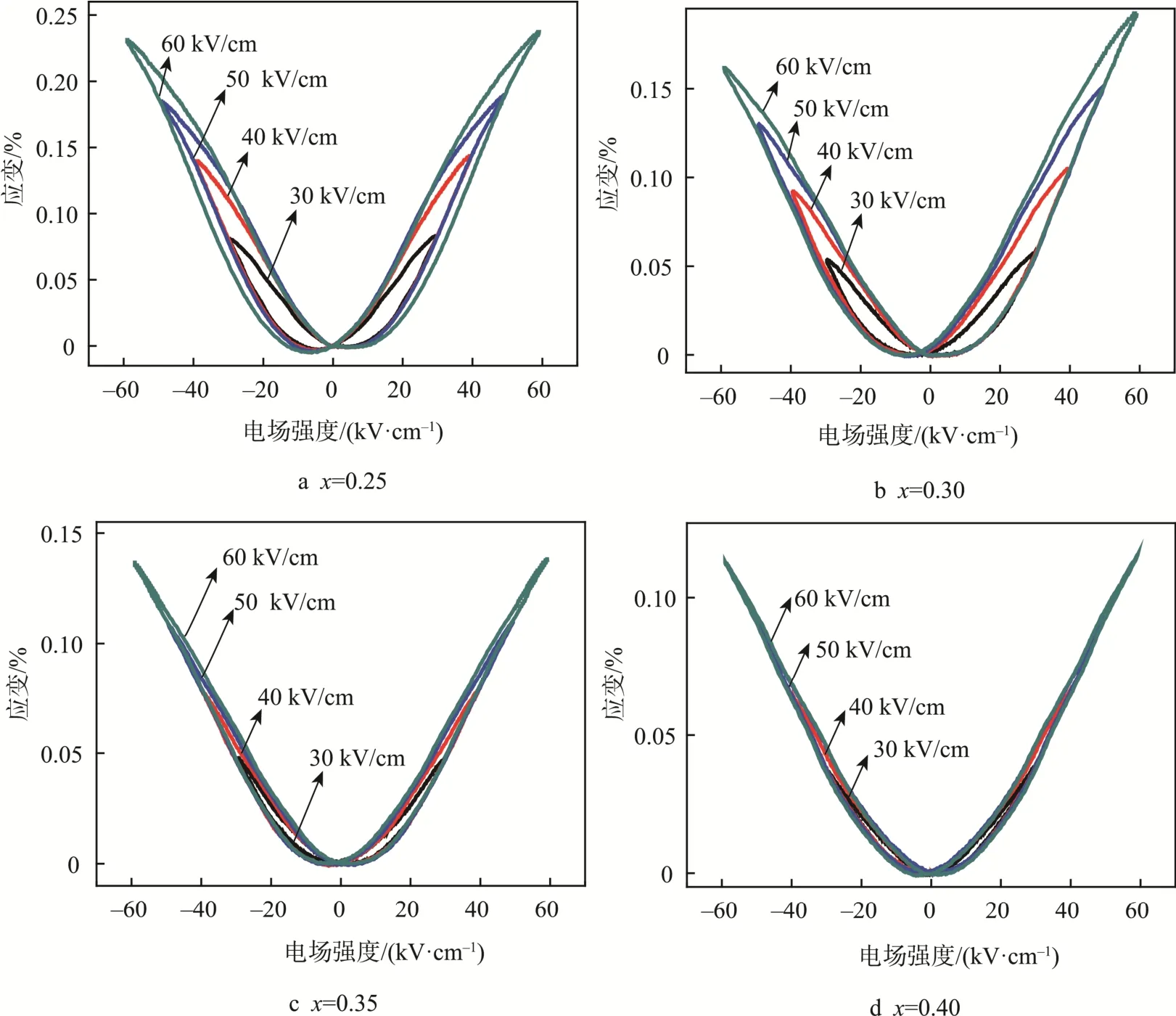
图5 不同电场强度时(1-x)[0.94NBT-0.06BT]-xST 陶瓷的应变曲线Fig.5 S-E curves of (1-x)[0.94NBT-0.06BT]-xST ceramics measured in different electric fields

为了分析电场强度和ST 含量对陶瓷应变性能的影响，研究了(1-x)[0.94NBT-0.06BT]-xST 陶瓷的应变及滞后性随电场强度的变化情况，见图6。由图6a可见，所有样品的应变随着电场强度的增大呈线性增大。随着ST 含量的增加，应变逐渐降低，在电场强度60 kV/cm 下其应变分别为0.24%、0.19%、0.14%、0.12 %。由图6b 可见，所测样品的应变滞后性随着电场强度的增大略有降低。x=0.25 和x=0.30 的样品表现出较大的滞后性，在电场强度60 kV/cm 下其应变滞后性分别为25.2%和22.8%。当ST 的物质的量分数增加至0.35 和0.40 时，应变的滞后性出现了明显的下降趋势。其中，x=0.40 的样品在电场强度60 kV/cm 下的应变滞后性降至7.8%，表现出典型的电致伸缩特征。应变滞后主要是由弛豫铁电体中的微畴在电场作用下的取向所致。随着ST 含量的增加，在室温时微畴的数目减少，位移量较小，回零性得到改善，即滞后性降低。

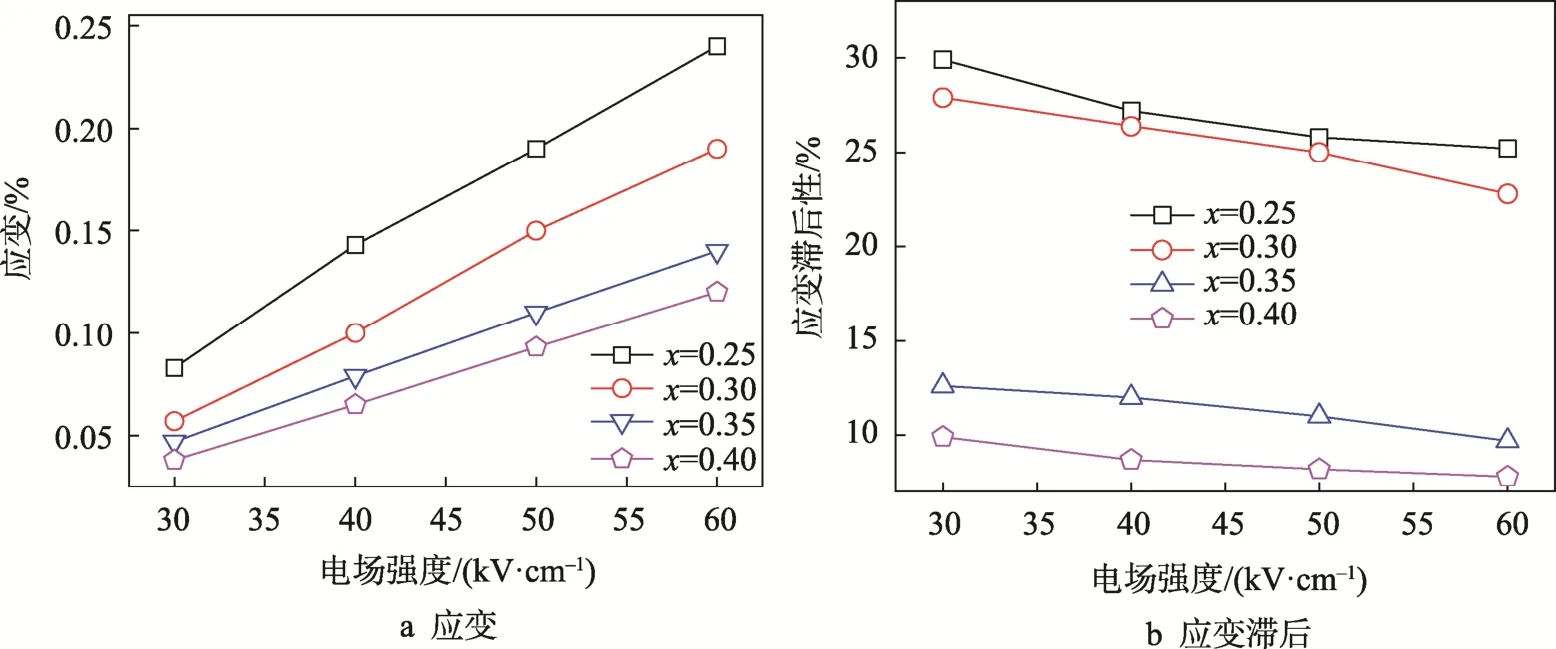
图6 (1-x)[0.94NBT-0.06BT]-xST 陶瓷的应变及滞后随电场强度的变化情况Fig.6 Variation of strain and hysteresis for (1-x)[0.94NBT-0.06BT]-xST ceramics measured in different electric fields

2.5 电致伸缩性能

当应变曲线为抛物线形，且应变与电场强度的关系没有滞后或滞后较小时，表明该材料具有良好的电致伸缩效应。根据电滞回线和应变曲线的分析可知，在x=0.40 时样品表现出基本无滞后的二次方的电致伸缩效应。铁电陶瓷的电致伸缩效应可以用S=QP2来评价，其中S为应变，P为极化强度，Q为电致伸缩系数。在室温下，x=0.40 时陶瓷在不同电场强度作用下的S-P2曲线和电致伸缩系数的变化情况见图7。由图7a可知，在所有电场强度下S-P2曲线均为一条倾斜的直线，表明x=0.40 时样品是一个无任何宏观铁电畴存在的理想电致伸缩材料。当电场强度由30 kV/cm 增至50 kV/cm 时，该样品的电致伸缩系数由0.020 2 m4/C2增大至0.021 3 m4/C2。当继续增大电场强度时，电致伸缩系数保持在0.021 3 m4/C2不变，该值远高于传统的电致伸缩材料 PMN（Q约为 0.017 m4/C2），且不低于目前文献中报道的无铅材料的电致伸缩性能[1,18]。

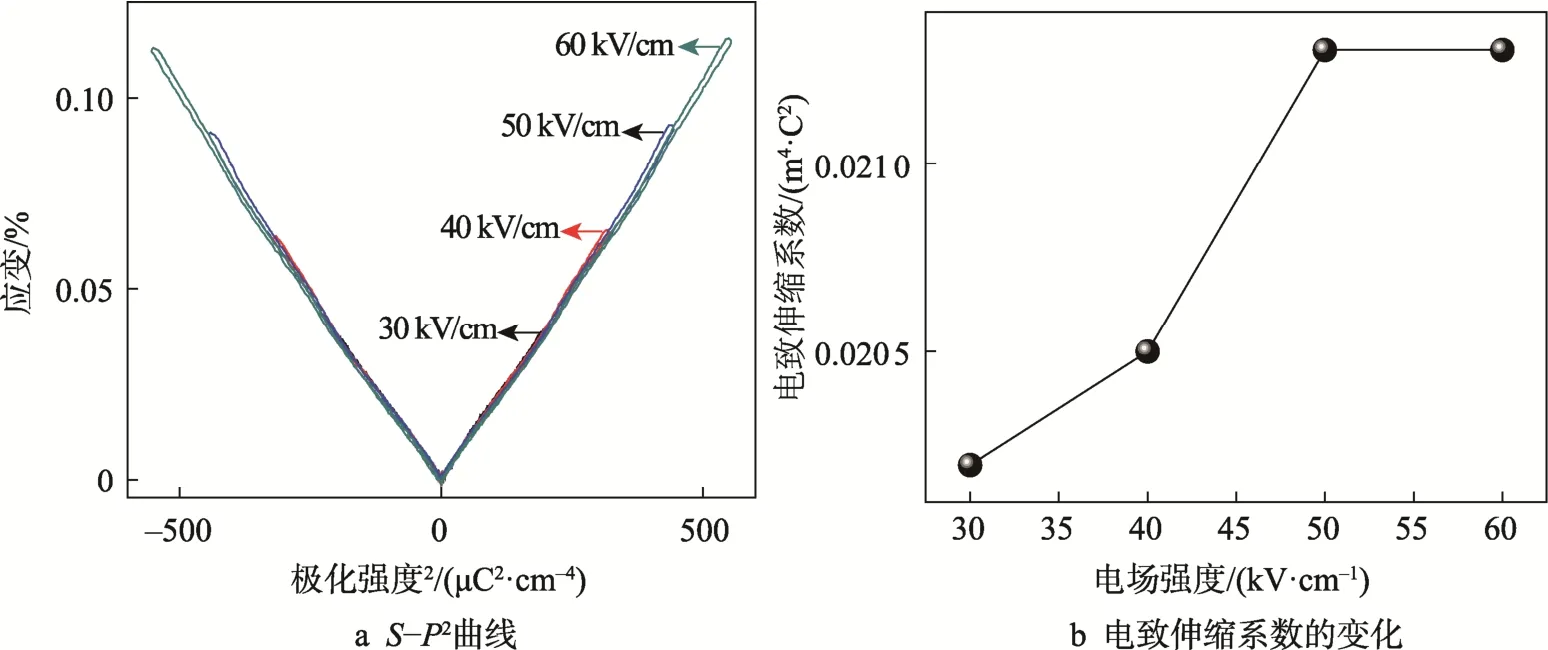
图7 室温下x=0.40 时陶瓷在不同电场强度下的S-P2 曲线和电致伸缩系数Fig.7 S-P2 curves and Q for the sample with x=0.40 measured at room temperature in different electric fields

3 结语

1）随ST 含量的增加，(1-x)[0.94NBT-0.06BT]-xST 三元系陶瓷的相结构由 R、T 两相共存(x为0.00～0.06)→T 相(x为0.08～0.20)→FE、RE 两相共存(x为0.10)→RE 相(x为0.25～0.40)。

2）R、T 两相共存区陶瓷的应变主要来源于逆压电效应引起的晶格变形和电场作用下的非180o畴转向。FE、RE 两相共存区陶瓷的应变主要来源于电场引发弛豫相和铁电相的相变，应变滞后性较大。RE相区陶瓷的应变主要来源于样品晶格本征变形产生的电致伸缩。

3）在弛豫相区，随着 ST 含量的增加，(1-x)[0.94NBT-0.06BT]-xST 陶瓷的弛豫性增强，应变和滞后性均降低。其中，x=0.40 的样品表现出典型的电致伸缩特征，其电致伸缩系数高达0.021 3 m4/C2。