数学新高考的考向研究与命题实践
——基于中国高考评价体系
黄 健
(江苏省苏州市教育科学研究院 215004)
精准把握教学方向、正确实施人才培养是每个教学工作者追求的目标.基于《中国高考评价体系》(下称《体系》)的新高考体现了国家教育部对教育根本问题的思考与探索,是创新驱动发展战略和科教兴国人才强国战略下的新要求.在深度研究新高考的基础上,笔者结合自身命题实践,谈谈数学新高考的特点以及对有效引导思维提升和能力发展的思考.
1 对《体系》的思考与启示
《体系》指出,高考的核心功能是立德树人、服务选材和引导教学.首先应引导学生树立正确的人生观、价值观,为国家培养具有积极思想、良好心态的后续人才,保证国家的持续性发展.其次,高考会聚焦核心素养,注重能力立意,加强开放探究,突出对逻辑思维和关键能力的考查,增强选拔功能,区分度会更为明显.再次,高考会通过展示文化与应用的广阔领域来引导教学回归基础、回归规律、回归本质,彰显数学的科学价值.
《体系》为我们梳理了正确的研究目标方向、科学的方法路径,提出了“价值引领、素养导向、能力为重、知识为基”的命题理念.新高考数学命题的首要任务是要体现试题价值,遵循学以致用的原则,坚决摒弃“构造类”和“技巧型”问题,避免试题与生活脱节,坚持应用导向,鼓励学生运用知识、能力和素养去解决问题.新高考数学命题对创新思维的要求会更高,会引入更多的问题情境,要求学生在现有经验与认识的基础上敏锐地发现新旧事物的关系,并利用推测、类比、联想、论证等手段创造性地解决问题,这是对学生核心素养考查的综合体现.
2 基于《体系》的考向研究与命题实践
2.1 强化概念辨析,深化数学理解
数学概念反映数学对象的数量关系和本质特征,是构成判断、推理、论证、拓展等思维的基础.正确理解数学概念,必须理解概念的内涵与外延.多选题型的加入,使得新高考对概念的考查有了更为宽阔的手段,除了传统的对基本概念的直接考查外,还增加了对概念的全方位辨析考查,在复习过程中要注意对概念的深度理解和类比迁移.
数学概念试题的呈现方向一是对相似概念的鉴别,突出纠错性,解题的关键点在于理解不同场景概念,有时需要融入实际情境进行甄别;二是平行概念的呈现,突出全面性,解题的关键点是要全面理解概念,不能有遗漏;三是抽象概念的转化,突出应用性,解题的关键点是要关注概念、公式、定理、法则的推导及拓广.
例1(2022苏州零模)下列命题正确的是( ).
A.若z1,z2为复数,则|z1z2|=|z1|·|z2|
B.若a,b为向量,则|a·b|=|a|·|b|
C.若z1,z2为复数,且|z1+z2|=|z1-z2|,则z1z2=0
D.若a,b为向量,且|a+b|=|a-b|,则a·b=0
命题意图 本题主要考查向量与复数的概念辨析,学生通过对相似概念的鉴别,巩固知识、深化理解.此外还可以联想实数与复数、向量与实数的概念对比,培养类比探究的思维习惯.
例2(2022苏锡常镇二模)随着北京冬奥会的举办,中国冰雪运动的参与人数有了突飞猛进的提升.某校为提升学生的综合素养、大力推广冰雪运动,号召青少年成为“三亿人参与冰雪运动的主力军”,开设了“陆地冰壶”“陆地冰球”“滑冰”“模拟滑雪”四类冰雪运动体验课程.甲、乙两名同学各自从中任意挑选两门课程学习,设事件A=“甲乙两人所选课程恰有一门相同”,事件B=“甲乙两人所选课程完全不同”,事件C=“甲乙两人均未选择陆地冰壶课程”,则( ).
A.A与B为对立事件 B.A与C互斥
C.A与C相互独立 D.B与C相互独立
命题意图 本题主要考查事件的概念辨析,选择分支比较抽象,需要合理转化,和2021年全国I卷第8题理念一致.选项A,B,让学生直观想象求解,缩短解题时间;选项C,D,需通过独立事件的计算公式验证,引导学生做好对概念的提炼和梳理.
2.2 基于实际情境,彰显应用价值
新高考数学卷强调基于实际情境的考查,“生活实践情境”和“探索创新情境”[1]的引入给高考试题带来了全新的面貌.学生通过阅读、理解、猜测、探求、归纳等手段解决问题,经过长期积累整理出一般的解题模型,体会数学的应用价值,提升阅读理解能力,发展数学建模素养.
情境一般取材于社会热点问题、改革开放伟大成果及数学史的经典案例,培养学生爱国主义精神和民族自豪感,其呈现方向一是基于我国科技领域的新成果,鼓励人才创新;二是基于经典文化领域,注重学科交叉;三是基于生活实践和民生领域,体现学以致用.

(1)求两超市的月需求总量为1 000件的概率.
(2)已知企业对此罐头的供货价格为30元/件,生产此罐头的成本为:800件内(含800)为20元/件,超过800件但不超过1 000件的部分为15元/件,超过1 000件的部分为10元/件.企业拟将月生产量X(单位:件)定为800或1 000或1 200.若两超市的月需求总量超过企业的月生产量,则企业每月按月生产量供货,若两超市的月需求总量不超过企业的月生产量,则企业每月按月需求总量供货.为保障食品安全,若有多余罐头企业每月自行销毁,损失自负.请你确定X的值,使该企业的生产方案最佳,即企业每月生产此罐头的利润Y的数学期望最大,并说明理由.
命题意图 本题以商品买卖问题为情境考查随机事件的概率与数学期望,并通过对数学期望的计算来制定决策,学生在处理问题中应理清成本、利润等关系,感悟数学手段的广泛应用,培养学习兴趣.
说明本题也可融入对统计相关量的考查,并可将进货量X规定在某个区间范围内连续变动,与实际联系更紧密,让学生感受方法的统一和思维品质的提升.变式如下:
某连锁超市欲从一家食品企业购进一种海鲜罐头,每件罐头食品的基本批发价为20元.如果进货数量在1 000件到1 200件之间(不含1 000件,含 1 200件),超出的部分每件打9折;如果进货数量大于1 200件(不含1 200件),超出的部分每件打8折.该超市准备以每件30元的零售价格在市场上销售这种海鲜罐头,为保障食品安全,到期未能售出的罐头就地销毁.为了解需求量情况,该超市通过市场调研,绘制了如图1所示的频率分布直方图.

图1
(1)请利用频率分布直方图的组中值估算该食品的平均市场需求量n;
(2)以各组需求量的频率作为各组需求量发生的概率,假设实际销售量为市场最大需求量.考虑到实际情况,超市决定将进货量X(单位:件)定在800件到1 400件之间,则X为多少时,利润Y的数学期望最大?
2.3 基于数据特征,考查分析想象
命题者凭借自身较强的观察能力和创造能力,对原问题的本质特征进行深入分析与研究,找出“已知”与“所求”之间的联系纽带,编制合适的替代条件,将问题“改头换面”.这里的数据特征,不仅是问题对象的代数式特征,还包括几何、背景等属性特征.
基于数据特征的试题呈现方向一是基于代数特征,强调变形能力与换元能力,要求学生通过观察代数式特征,尝试变形或换元,探寻问题本源;二是基于几何特征,注重图形溯源与运算优化,要求学生通过图形感知挖掘几何背景,优化解题的途径;三是基于高等背景,注重形式和问题类比迁移,要求学生提升知识宽度和探究能力,努力寻找问题关联,从而加深认识、突破难点.

命题意图 本题考查函数的零点问题,解题的关键是要通过观察函数表达式特征发现其为偶函数,将问题转化为研究在(0,+∞)上的零点个数,达到简化运算的目的,要求学生有较强的洞察力和知识迁移的能力.
说明将函数表达式进一步抽象化,有如下变式:

分析令t=x-1,则g(t)=f(t)+f(-t)为偶函数,问题转化为函数g(t)在(0,+∞)上有两个零点,下略.
例5(2022苏州大学考前指导卷)已知x1,x2,x3(x1 命题意图 本题考查多元最值问题,应在充分理解零点定义的基础上寻找合适的转化路径,由函数表达式的特征发现其对称性是解题关键. 命题意图 本题考查点到直线的距离,渗透数形结合与转化化归思想.常规处理是平移已知直线与函数图象相切,进而转化为求已知直线与切线的距离.事实上,此题源于高等的切线不等式背景: 数学探究是一个活动或者一个过程,它包括:观察分析数学事实,发现并提出有意义的数学问题,数学探究猜测、探求适当的数学结论或规律,给出解释或证明.数学探究有助于学生体验知识产生、发展、完善的过程,树立科学严谨的态度和不畏困难的精神,在质疑和反思中提高发现、提出、分析、解决数学问题的能力. 开放探究问题的呈现方向一是重视对研究对象通性的考查,结论不单一,思维多样化,要求学生全方位理解对象属性;二是对动态图形中的结论探究,考查定理、思想的灵活运用,要求学生能够分析出动态过程中对象变化的规律;三是调整逻辑关联、转变逻辑方向,直接指向对概念的深度考查,强调基础性.[1] 例7(2022苏锡常镇二模)已知圆锥同时满足条件:①侧面展开图为半圆;②底面半径为正整数.请写出一个这样的圆锥的体积V=. 命题意图 本题考查简单几何体的侧面积和体积、圆锥的侧面展开图.引导学生经历对公式的回忆及表达,全方位完善知识结构,从而提升关键能力和学科素养. (1)证明:sinA=2sinB; (2)求所有正整数k,m的值,使得c=mb和 tanA=ktanC同时成立. 命题意图 本题考查解三角形,第(2)题以探究性问题形式呈现,体现数论方法与三角知识的融合,激发学生的探索欲,有效区分了学生间的差异. 新高考全国卷正在努力打破数学知识间的壁垒,寻找试题的新的呈现方式.在考查方式上更加突出综合性[1],强调能力立意,要求学生能够揭开问题表面的面纱,深入到问题的本质中去. 注重知识交叉的试题呈现方向一是知识载体的融合贯通,彰显呈现方式的灵活性;二是研究目标的适度变化,彰显知识板块的发展性,培养创新意识;三是思想方法的多元考查,彰显能力考查的多样性. C.对任意n∈N*均有an+bn≤cn D.存在n∈N*使得an+bn>cn 命题意图 本题以二项式为载体,考查不等式与数列问题.试题呈现方式灵活,研究目标多变.学生若对概念和基本思想有深刻理解,则不难解决该问题. 例10(2022苏州零模)已知函数f(x)=ln(ex-1)-lnx. (1)判断f(x)的单调性,并说明理由; 命题意图 本题聚焦函数导数与数列、不等式的有机融合,重点考查导数的综合运用,通过载体融通实现目标变化,融合“联想”“构造”“迭代”“放缩”等多种思想方法,实现对逻辑推理核心素养的考查. 说明此题源于2020年教育部考试中心为山东省命制的新高考模拟卷,原题如下: (1)求a;(2)讨论g(x)=x(f(x))2的单调性;(3)设a1=1,an+1=f(an),证明:2n-2|2lnan-ln 7|<1. 逻辑思维能力是学习数学的根本能力,它是借助问题条件,通过寻找依据、层层递进等思维形式进行思考与活动的能力.提升学生的思维品质是数学学科的根本任务.新高考全国卷题型最显著的变化是增加了逻辑证明题的数量,力求全方位考查学生的思维习惯和思维品质,要求学生能准确而有条理地表达自己的思维过程,包括分析、推演、说理、论证等环节.教师应及时贯彻国家方针,努力帮助学生提升逻辑推理能力,强化理性思维,培养创新能力. 注重逻辑推理的试题呈现方向一是重视充要关系的辨析,完善知识网络,以此来改变教学中忽视概念细节的情况;二是重视基于概念的探究,揭示命题背景,体验试题价值;三是重视高等背景的延伸,体现考点融合,体现综合性与创新性[1]原则. 例11(2022苏锡常镇二模)在平面直角坐标系xOy中,已知抛物线C:y2=4x的焦点为F,准线为l,过点F且斜率大于0的直线交抛物线C于A,B两点,过线段AB的中点M且与x轴平行的直线依次交直线OA,OB,l于点P,Q,N. (1)判断线段PM与NQ长度的大小关系,并证明你的结论; (2)若线段NP上的任意一点均在以点Q为圆心、线段QO长为半径的圆内或圆上,求直线AB斜率的取值范围. 命题意图 本题聚焦对直线与抛物线位置关系的考查,检测学生的字母运算能力.试题追求理性思维和数学探索,要求学生在经历逻辑推理的过程中体会数学的重要性. 图2 新高考数学全国卷注重基础、体现方法、突出思想、考查能力,考查学生的数学素养和探究意识.在《体系》的引领下,教师应努力转变教学观念,构建有价值的教学模式,对学生的思维能力、创新意识、问题意识及合作意识开展高质量培养.在新课教学中,教师要培养学生的开放探究意识,通过开放性设问、连续型套问、拓展性追问、纠错式反问等方式帮助学生领悟问题、发展思维.在解题教学中,教师应关注课标理念、重视四基落实、立足数学本质、优化示范引领,通过一题多解、多角度探源、变式拓展、总结提炼等方法引导学生探寻本质、理解背景.作为教育主管部门,应当呼吁和鼓励更多的教师参与命题研究,在实践中体会《体系》的理念,从而更为精准地了解学情,把握教学方向.

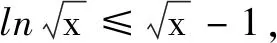
2.4 尝试开放探究,有效区分差异

2.5 注重知识交叉,彰显能力立意
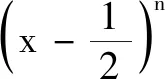
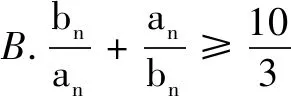


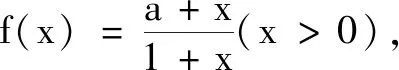
2.6 注重逻辑推理,发展理性思维


3 结语

