基于贝叶斯LSTM 的风电功率概率性预测研究

冯惠丽

（中国大唐集团科学技术研究总院有限公司，北京 100000）

随着化石能源的枯竭，可再生能源的开发已经引起了全世界的广泛关注。由于风能无污染、分布广等优点，风力发电技术近年来发展迅速。然而，风能的间歇性和波动性将极大地影响电力系统的安全性和稳定性。因此，准确可靠的风电功率预测对于促进合理的电力调度和安排停机维护以保证电力系统的稳定运行至关重要[1-2]。

一般来说，根据预测范围，风电功率预测可以分为4 种类型：超短期、短期、中期、长期[3]。超短期风电功率预测旨在保证电网实时稳定调度和高质量供电。短期预测的目的是制定发电计划，安排区域调度，调整检修计划。中长期预测主要服务于对预测精度要求不高的风电机组和输电线路的维护计划。为了满足风电功率预测的不同需求，研究开发了多种预测模型。一般来说，这些预测方法可以分为2 类：物理方法、统计方法。前一类方法主要依靠数值天气预报（NWP）信息，这通常适用于中长期风电功率预测[4]。相反，统计方法试图基于历史时间序列数据开发经验模型，适用于超短期及短期预测的数据驱动模型。其中每种风电功率预测类型又分为点预测和概率预测，点预测常见统计模型主要基于自回归综合移动平均法（ARⅠMA）[5]、人工神经网络（ANN）[6]和卡尔曼滤波器[7]等。但点预测方法侧重于未来某个时间点的预报，而不考虑预测不确定性的估计。而概率预测模型还可以提供预测的置信区间，适用性越来越强[8]。

本文基于贝叶斯神经网络，结合LSTM 提取时序数据特征的优势，构建了贝叶斯LSTM 网络，通过多种仿真实验可知，本文所提方法具有较好的概率预测效果。

1 贝叶斯LSTM（Bayesian LSTM）神经网络

1.1 贝叶斯神经网络

对于依赖于新输入样本x及权重W有输出y（x；W）的神经网络模型来进行回归预测时，其参数积分如下：

式（2）中：P（W｜D）为权重的后验分布。

设P（W）是在取得训练数据前对神经网络权重W的先验分布，那么定义如下正则化器：

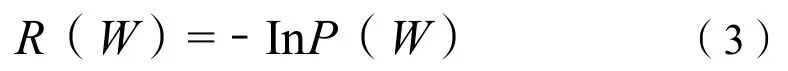
则基于贝叶斯规则并结合式（2）（3）可得：

式（4）中：const 为常数。

另贝叶斯神经网络回归预测模型的总误差函数为U（W）=E（W）+R（W），则可依式（4）得：

式（5）中：Z为归一化常参数。

将式（5）与式（2）合并可得：

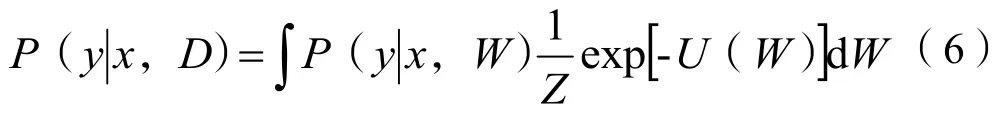
则神经网络的预测变为对式（6）的计算，可式（6）没法直接求得其解析解，需要借助诸如马尔科夫链蒙特卡洛（MCMC）等数值积分近似法来解。

假设马尔可夫链具有遍历性，那么通过在此链上的大量采样所趋于的稳定分布便能够表征式（5）的后验概率分布。用结果马尔可夫链上的样本序列｛Wt｝，则针对式（6）积分的近似计算式如下：

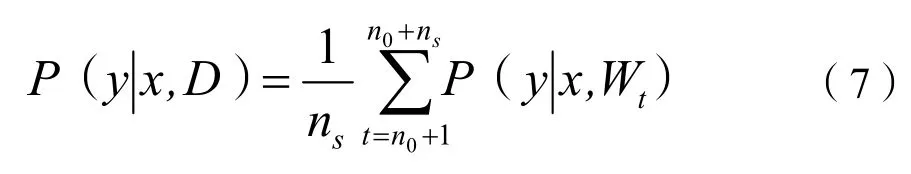
式（7）中：n0为为保证收敛性而舍弃的一些初始马尔可夫链；ns为平衡后验分布的权重向量样本数。

1.2 贝叶斯LSTM 网络结构

LSTM 是目前机器学习领域中广泛使用的深度学习方法，由 HOCHREⅠTER 等[9]在 1997 年提出。LSTM是专门用于处理时间序列数据的深度学习模型，其在网络模型中加入门控制器，可以解决RNN 中的长期依赖问题（梯度爆炸或消失），结构如图1 所示。

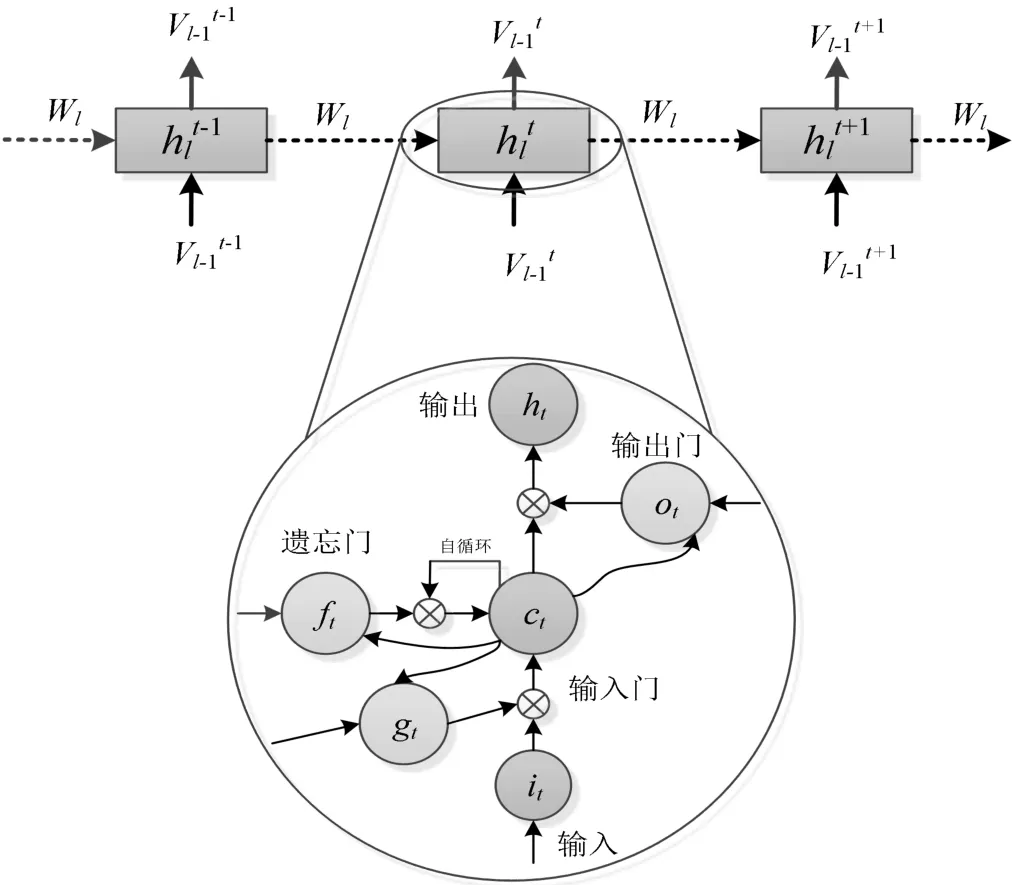
图1 LSTM 结构图

LSTM 模型在原有的短期记忆单元ht的基础上，增加一个记忆单元ct来保持长期记忆，同时增加3 个门控机制来控制整个学习过程中的信息流。LSTM 单元在每个时间步长t的状态被定义为一组5 个向量Rd：输入门it、遗忘门ft、输出门ot、隐藏状态ht、存储单元ct。d是LSTM 单位的数量。LSTM 传递函数为：

式（8）中：σ为sigmoid 函数；W和b为权重和偏置参数；xt为当前输入。

遗忘门控制从存储单元删除不需要的信息，而输入门控制向存储单元添加新信息，输出门控制内部存储状态的暴露。通过3 个门，存储单元ct可以选择性地更新、删除和遗忘内部信息，从而更好地理解序列中的长期依赖性，提取时序数据中隐藏特征。

本文利用上述LSTM 网络处理风电功率历史运行数据，提取时序数据关联特征，随后将学习的趋势特征送入贝叶斯神经网络，构建了贝叶斯LSTM 预测模型。

2 基于贝叶斯LSTM 的风电功率概率性预测

2.1 风电特征输入构建

风电功率与多种因素相关，包括历史风电功率、各气象因素，如风速、风向、温度以及气压等。但各因素对风电功率预测的影响程度不一样，如果把所有因素均送入深度学习网络，一方面造成模型结构复杂、参数众多，效率也会较低，同时与风电功率相关性较低的因素的加入对预测模型来说是一种噪声干扰，会带来负面影响，从而降低模型的预测精度。因此，需要对风电数据集进行相关性分析，剔除价值小的因素，同时也可降低数据维度。

本文采用Pearson 相关系数法计算风电历史数据集中不同因素与当前时刻风电功率的相关程度，其中二维变量的Pearson 相关系数计算公式如式（9）所示：

通过Pearson 相关计算分析，比较前一时刻的各个因素与下一个时刻风电功率的相关性大小，选取合适的输入变量。相关性分析结果如表1 所示。

表1 各因素与光伏功率的Person 相关系数

从表1 可知，各气象因素与风电功率的Person 相关系数由大到小分别是风速、风向、温度和气压，也即风速和风向与风电功率相关性最高，均大于0.5。

为了最大程度平衡训练精度和训练效率的关系，本文最终将Person 相关系数较高的前两种气象因素，风速和风向作为风电功率贝叶斯神经网络预测模型最终的输入变量，同时，如前文所述，通过LSTM 对风电历史运行数据进行特征构建后亦作为输入喂给贝叶斯神经网络。

2.2 概率预测评价标准

本文采用了2 种常用的概率评分方法。一个是弹球（pinball）失分，可以综合表示可靠性和锐度，另一个是Winkler 评分，可以表示预测区间的锐度和无条件覆盖度。

pinball 失分是对任何分位数q∈（0，1）的加权绝对误差度量，可表述为：

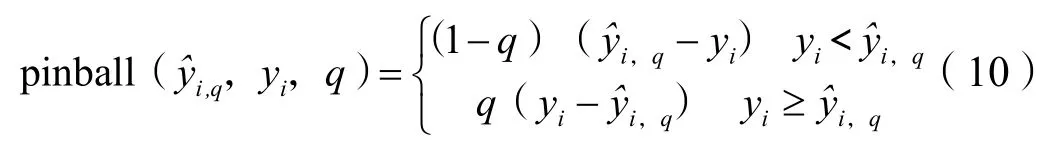
概率预测的总体弹球损失分数可以通过累积预测范围内所有目标分位数的弹球损失来获得。弹球损失越低，预测效果越好。

对于（1-α）×100%置信水平，Winkler 得分定义为：

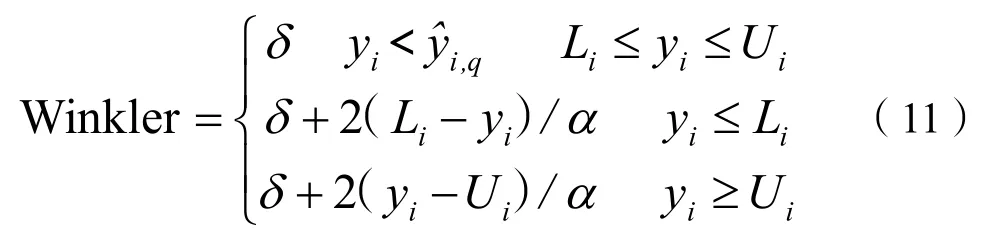
式（11）中：δ=Ui-Li为区间宽度；Li和Ui分别为预测区间的下界和上界。

如果实际功率值落入预测区间，那么Winkler 分数仅取决于预测区间宽度。否则，由于惩罚因子，分数会很高。分数越低，表示预测效果越好。

3 仿真验证

3.1 数据集

风力发电数据集取自2017 年至2019 年26 311 h的ERCOT 每小时总风力输出[10]。数据显示了德克萨斯州所有风力发电机的总输出功率。总装机风力发电量从16 246 MW 增加到22 607 MW，最大风力输出为19 099 MW。负荷的最大风力输出百分比为54.6%，出力百分比变化最大为280.6%。在26 311 h 的数据中，70%、10%和20%的部分分别用于训练、验证和测试集。

3.2 预测效果

为了测试本文所述网络的实际可行性和优越性，本文分别在80%和90%两种置信水平下进行了光伏功率概率预测，并在80%置信水平下，与正态分布法和持续区间预测法进行了对比验证。

80%置信水平下预测区间如图2 所示，90%置信水平下预测区间如图3 所示。从图2 和图3 可知，基于贝叶斯LSTM 神经网络的风电概率预测模型可及时对功率波动作出响应，给出下一预测点功率可能的波动范围，且准确率较高。

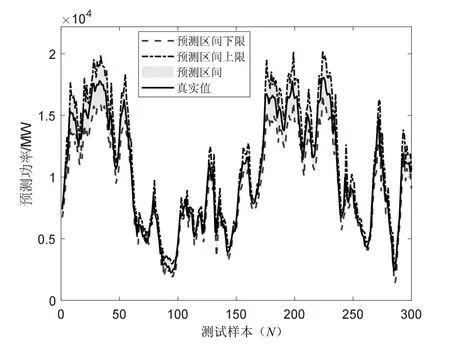
图2 80%置信水平风电功率概率预测

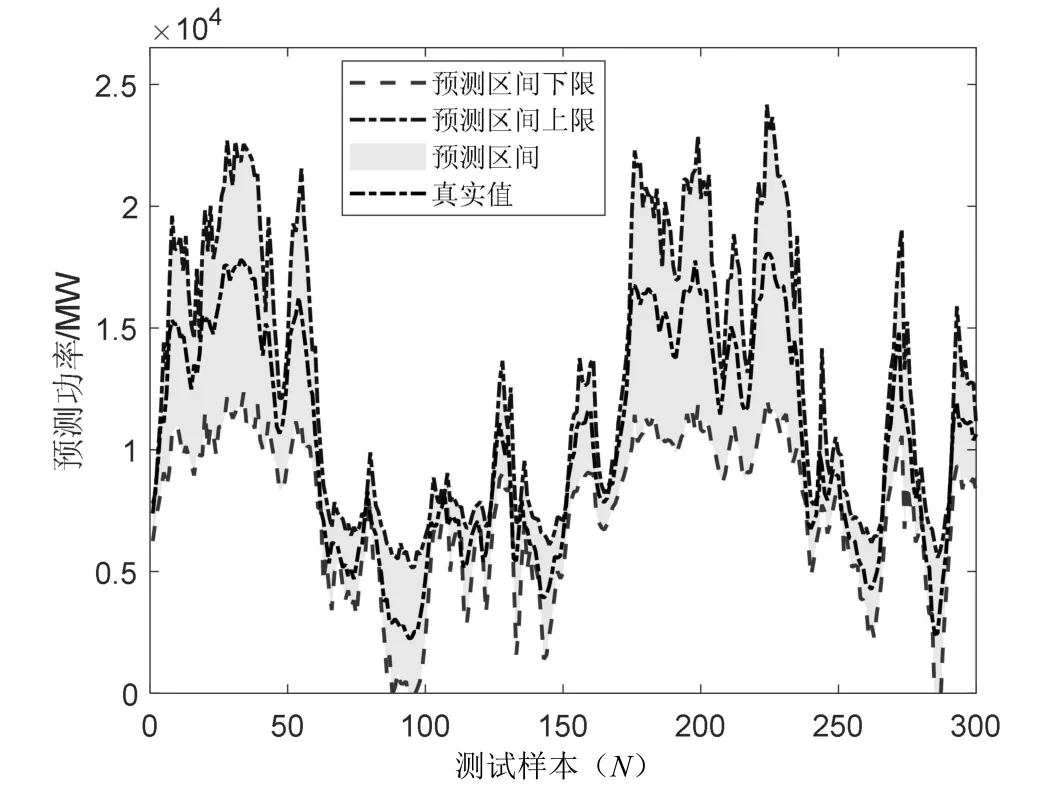
图3 90%置信水平风电功率概率预测

不同算法风电功率预测区间对比示意图如4所示。风电概率预测性能对比如表2 所示。

结合图4 以及表2 可知，将本文方法与正态分布法及持续区间预测法进行对比，从表2 的pinball 指标和Winkler 指标可知，本文所提方法的预测效果更好。

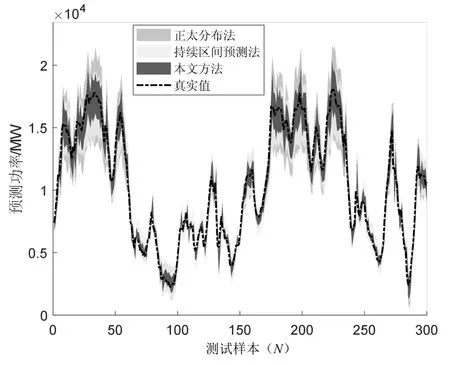
图4 不同算法风电功率预测区间对比示意图

表2 风电概率预测性能对比

4 结论

针对风电功率确定性点预测无法对风电功率波动进行预测的问题。本文基于贝叶斯神经网络，结合LSTM 提取时序数据关联特征的特有优势，构建了贝叶斯LSTM 预测模型。并以皮尔森相关系数法对影响风电功率预测的复杂气象输入因素进行了相关性计算，剔除了与风电功率相关性低的因子，降低了输入维度和输入噪声，最后以降维后的气象因子以及LSTM 处理后的功率历史时序数据为最终输入，通过80%和90%两种置信度下的预测仿真以及与正太分布法和持续区间预测法的对比验证，可知本文能更好地对风电功率波动性进行预测。