从“充分与必要”视角辨析一道三角题的解法
兰诗全
(福建省古田县第一中学 352200)
“问题是数学的心脏”,找到答案只是数学解题的前一半,更重要的是解题后的反思.“不思故无惑,不惑故无问,不问故无得.”为什么是正确的、为什么是错误的、错在哪里呢,对这些“为什么”的追问一定可以大大提升分析、解决数学问题的能力.反思才能悟出其中的方法与思想,反思才能悟出问题的真本质、真规律、真道理.
以下从充分与必要视角对一道题目的多种解法进行正误辨析,以示解题中要对充分与必要条件加以高度重视,理清思路、认识到位、理解深刻,要发现规律,要揭示本质,才能真正掌握知识,提高解题能力,提升数学素养.
题目在锐角三角形ABC中,角A,B,C所对的边为a,b,c,若b2=ac,求cosB的取值范围.

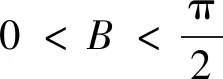
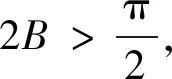
辨析很多学生认为以上解法是正确的,但事实上是错误的.这又是为什么?细想b2=ac这个条件用到位了吗?没有用到位,没有用充分!由b2=ac⟹b不是最长边也不是最小边(不妨设a≤b≤c)⟹A≤B≤C,但反过来由A≤B≤C推不出b2=ac,即b2=ac内在的本质关系未充分利用,错解2也是条件不等价变形造成的!利用已知条件的必要条件A≤B≤C来解答就得出问题的解,这与解法1类似,往往会扩大所求的取值范围.
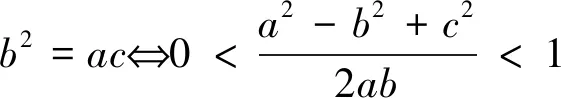

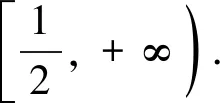
正解1 由b2=ac,得b不是最长边也不是最小边,不妨设a≤b≤c,则A≤B≤C.


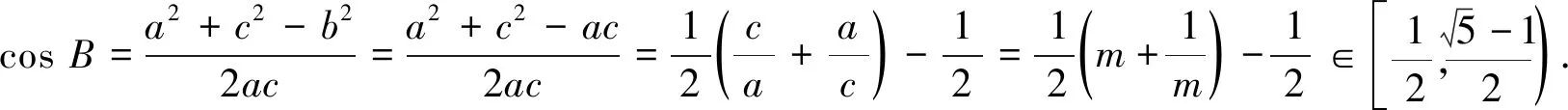
辨析以上解法正确吗?“水本无华,相荡乃成涟漪;石本无火,相击而发灵光.”经过广泛讨论,积极思考后又有学生认为不对,理由是因为首先要构成三角形,从而在上述解法的基础上还应满足条件a+b>c,故有以下正解2.
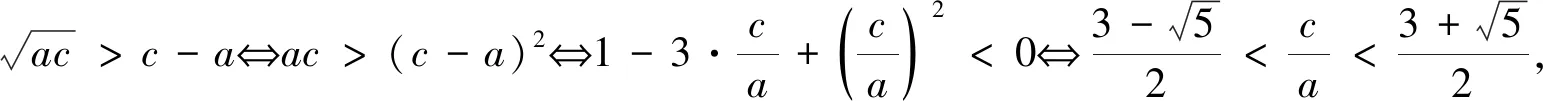
辨析正解1与正解2的最后答案是一样的,这是偶然还是必然?要想找出内在本质规律,要想打破砂锅问到底,此问题还应从以下命题说起.
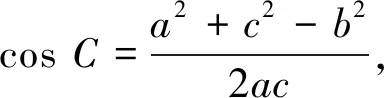
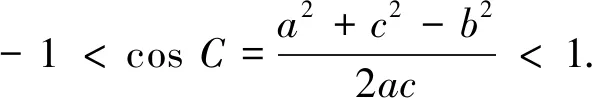
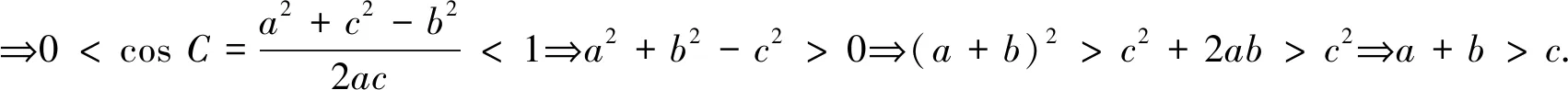
经常性地像这样进行数学问题辨析,错中求正、败中求胜,数学问题将越辨越清,认识将越来越深刻.数学学习若不能揭示问题的本质,则对知识方法认识依然“云里雾里”,不能从错误的阴影中真正走出来,不能从正确中掌握规律,这是数学学习的大忌.以上辨析说明,对充要条件是否准确应用直接关系到解题的成败,许多时候解题出错都是因为充要关系没用对,对充要条件的应用要特别注意,已知条件的相互转化要注意充要性,一定要利用已知条件或与已知等价的条件来解题,这是本质,这是关键.
——辨析“凌乱、混乱、胡乱、忙乱”

